|
|
Методическое пособие с задачами - Динамика. Методическое пособие для студентов очнозаочной формы обучения Издание второе, исправленное и дополненное Направления (специальности)
Таблица Д4б (к рис. Д4.5-Д4.9)
Номер условия
| Углы, град |
с,
Н/см
|
M1
|
M2
|
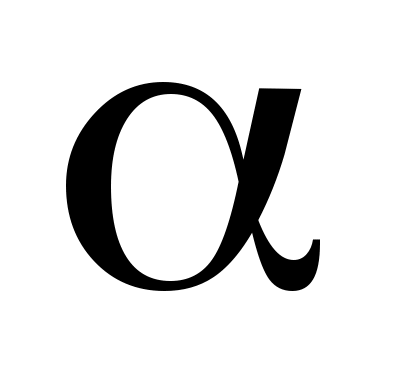
|
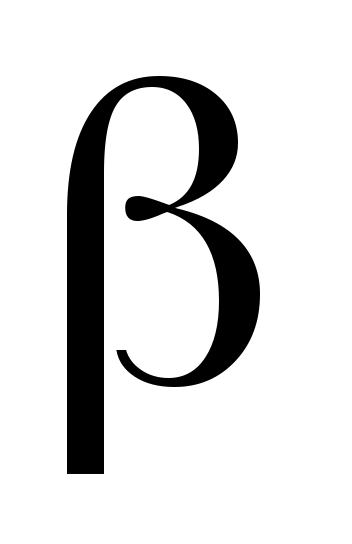
|
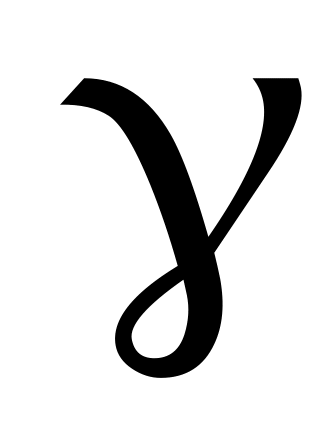
|

|
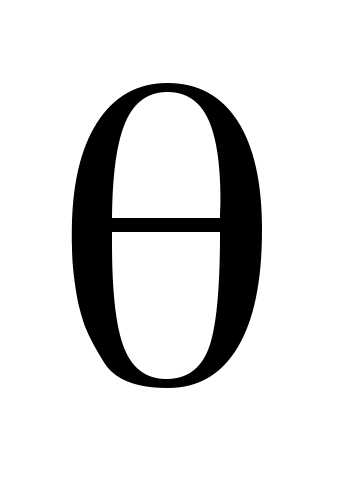
|
0
|
30
|
30
|
60
|
0
|
150
|
80
|
200
|
340
|
1
|
0
|
60
|
60
|
0
|
120
|
90
|
220
|
320
|
2
|
60
|
150
|
120
|
90
|
30
|
100
|
240
|
300
|
3
|
30
|
60
|
30
|
0
|
120
|
110
|
260
|
280
|
4
|
90
|
120
|
150
|
90
|
30
|
120
|
280
|
260
|
5
|
30
|
120
|
150
|
0
|
60
|
130
|
300
|
240
|
6
|
60
|
150
|
150
|
90
|
30
|
140
|
320
|
220
|
7
|
0
|
60
|
30
|
0
|
120
|
150
|
340
|
200
|
8
|
90
|
120
|
120
|
90
|
60
|
160
|
360
|
180
|
9
|
90
|
150
|
120
|
90
|
30
|
180
|
380
|
160
|
Принцип возможных перемещений
(краткие сведения из теории)
Возможным перемещением механической системы называется совокупность
а) бесконечно малых
б) мысленных
перемещений точек системы, при которых
в) не нарушаются связи,
наложенные на систему. Возможное перемещение любой точки системы будем изображать элементарным вектором 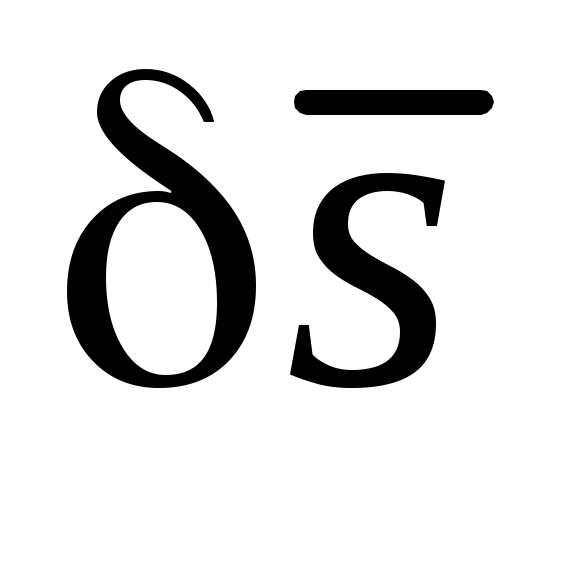 , направленным в сторону перемещения. , направленным в сторону перемещения.
Число степеней свободы. Число независимых перемещений точек системы называется числом степеней свободы системы. Если система состоит из n точек, на которые наложены k геометрических (не накладывающих ограничений на скорости точек) связей, то она имеет 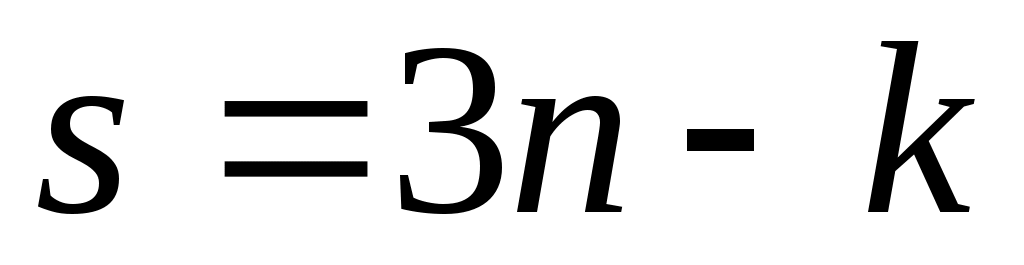 степеней свободы. В дальнейшем связи считаются геометрическими. Следовательно, чтобы задать положение такой системы в любой момент времени, не нужно задавать все координаты всех точек, а надо задать только независимые параметры. степеней свободы. В дальнейшем связи считаются геометрическими. Следовательно, чтобы задать положение такой системы в любой момент времени, не нужно задавать все координаты всех точек, а надо задать только независимые параметры.
Независимые параметры, число которых равно числу степеней свободы, и которые однозначно определяют положение всей системы в любой момент времени, называются обобщенными координатами и обозначаются
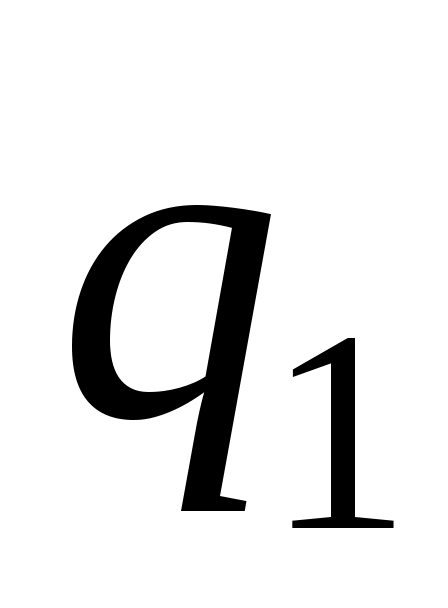 , , 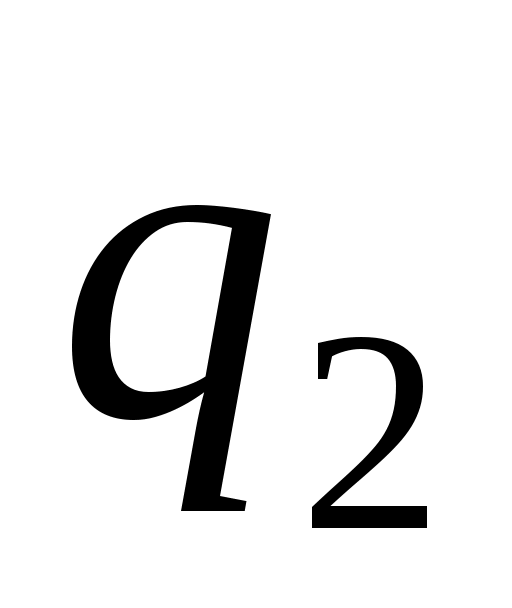 ,…, ,…, 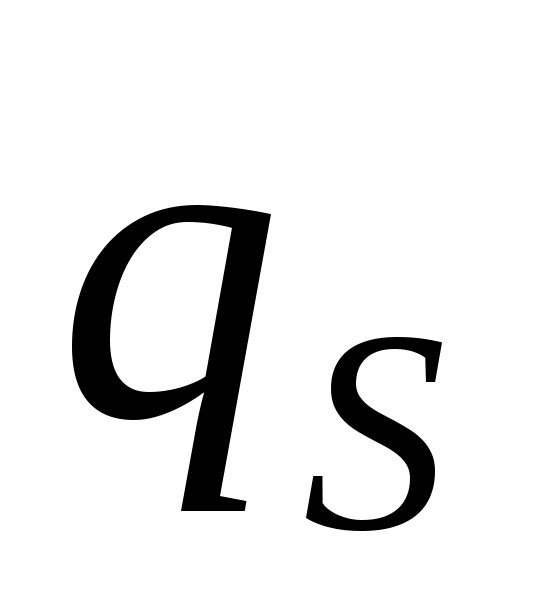 , ,
где s – число степеней свободы. В качестве обобщенных координат можно выбрать декартовы координаты точек, углы поворота тел и т.д.
|
Идеальные связи. Связи называются идеальными, если сумма элементарных работ реакций связей, наложенных на систему, равна нулю на любом возможном перемещении системы:
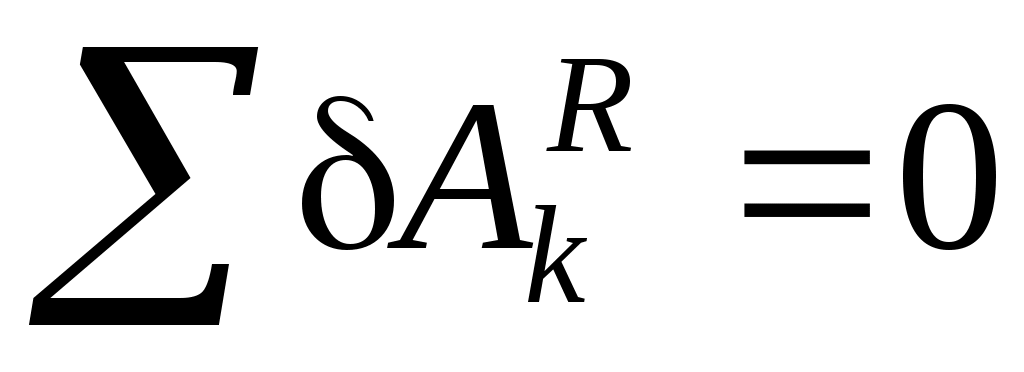 . .
(Элементарная работа на возможном перемещении обозначается  ). Все встречавшиеся ранее связи (шарниры, поверхности, нити, подшипники и т.д.) – идеальные при отсутствии трения. Если трение имеется и работа силы трения отлична от нуля, то сила трения включается в число активных сил. ). Все встречавшиеся ранее связи (шарниры, поверхности, нити, подшипники и т.д.) – идеальные при отсутствии трения. Если трение имеется и работа силы трения отлична от нуля, то сила трения включается в число активных сил.
Принцип возможных перемещений. Формулировка: для равновесия системы с геометрическими идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, действующих на точки системы, на любом возможном перемещении системы из данного положения была равна нулю:
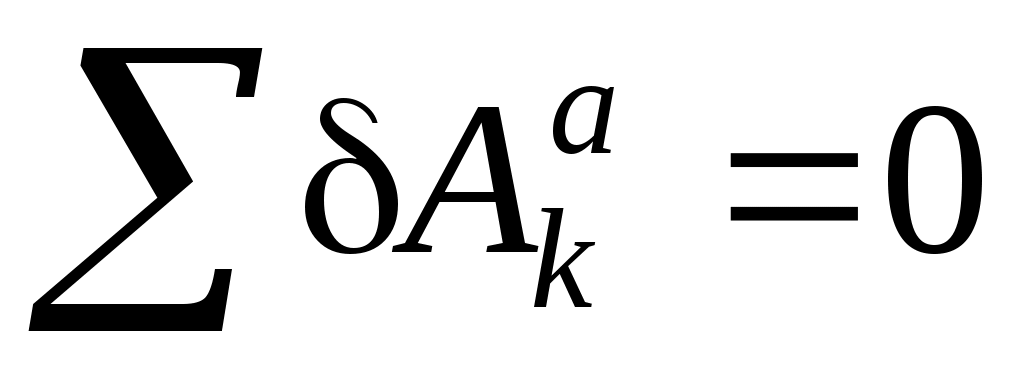 , (1) , (1)
или (с учетом выражений для элементарной работы силы, см. задачу Д4)
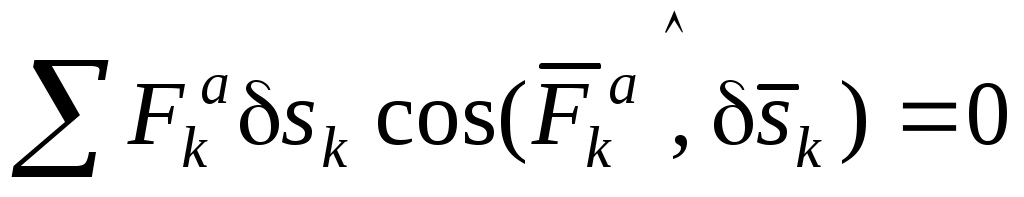 , ,
а также
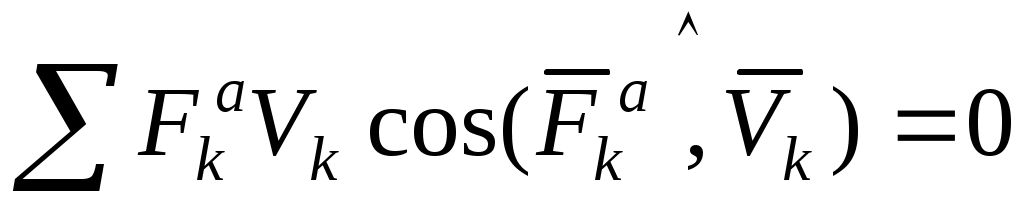 . (2) . (2)
В (2) выполнено деление на 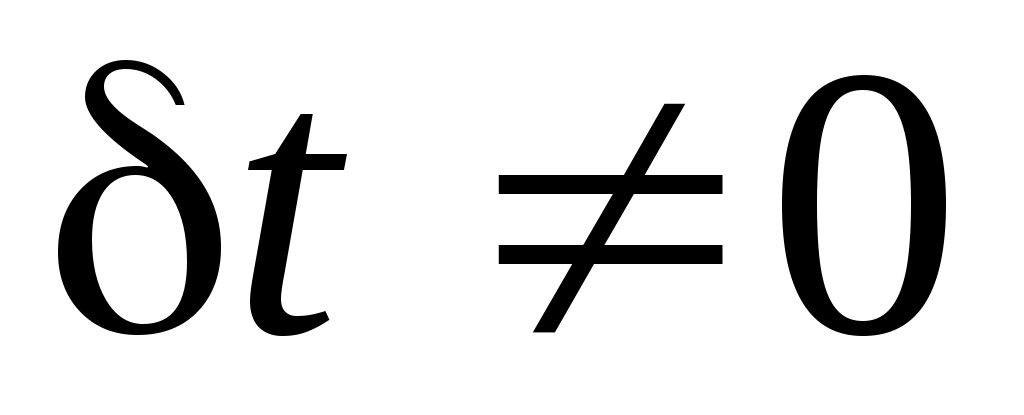 и поэтому суммируются мощности сил. и поэтому суммируются мощности сил.
|
Указания. Задача Д4 – на применение условия равновесия механической системы – принципа возможных перемещений. Механизм в рассматриваемой задаче имеет одну степень свободы, т. е. одно независимое возможное перемещение. Для решения задачи нужно сообщить механизму возможное перемещение, вычислить сумму мощностей всех действующих активных сил и пар на этом перемещении и приравнять ее нулю. Все вошедшие в составленное уравнение скорости следует выразить через какую-либо одну из них.
Чтобы найти деформацию пружины  , надо из полученного соотношения определить силу упругости F. На чертеже эту силу можно направить в любую сторону (т.е. считать пружину или растянутой, или сжатой); верно ли выбрано направление силы, укажет знак силы. , надо из полученного соотношения определить силу упругости F. На чертеже эту силу можно направить в любую сторону (т.е. считать пружину или растянутой, или сжатой); верно ли выбрано направление силы, укажет знак силы.
Последовательность действий при решении задачи см. в примере Д4.
Пример Д4. Механизм (рис. Д4а), расположенный в горизонтальной плоскости, состоит из стержней 1, 2, 3 и ползунов В, D, соединенных друг с другом и с неподвижной опорой О шарнирами. К ползуну В прикреплена пружина с коэффициентом жесткости с, к ползуну D приложена сила  , а к стержню 1 (кривошипу) – пара сил с моментом М. , а к стержню 1 (кривошипу) – пара сил с моментом М.
Дано: α= 60°, β = 0°, γ= 60°, φ = 0, θ= 120, l1 = 0,4 м, АЕ = ED, с=125 Н/см, М = 150 Hм, Q = 350 Н.
Определить: деформацию  пружины при равновесии механизма. пружины при равновесии механизма.
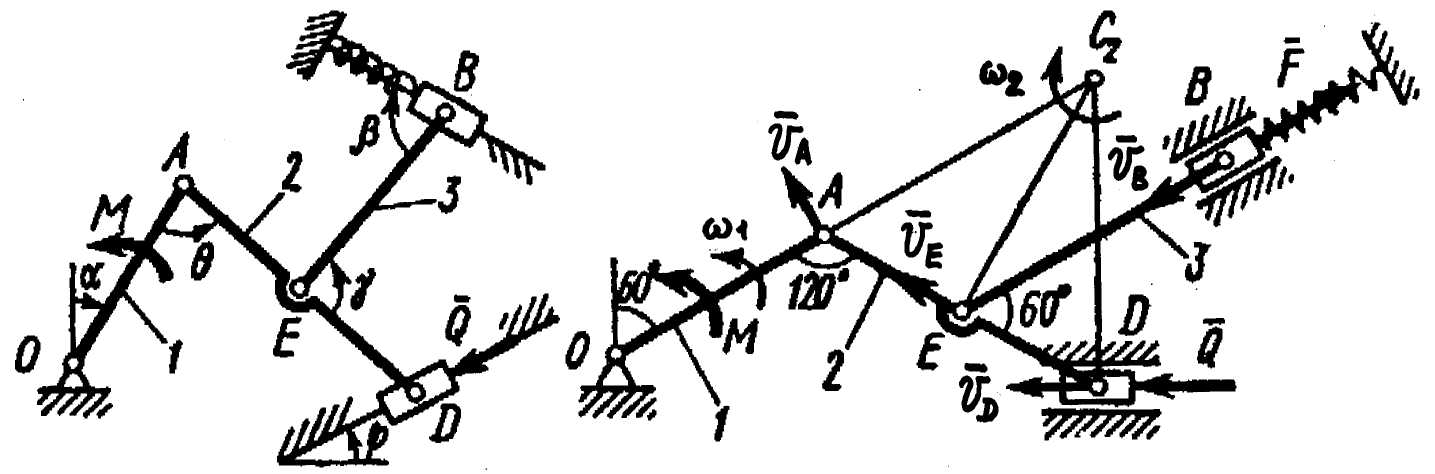
а) б)
Рис. Д4
Решение.
1. Строим положение механизма в соответствии с заданными углами (рис. Д4б); при этом, согласно указанию к задаче Д4, прикрепляем пружину к ползуну с другой стороны (так, как если бы было 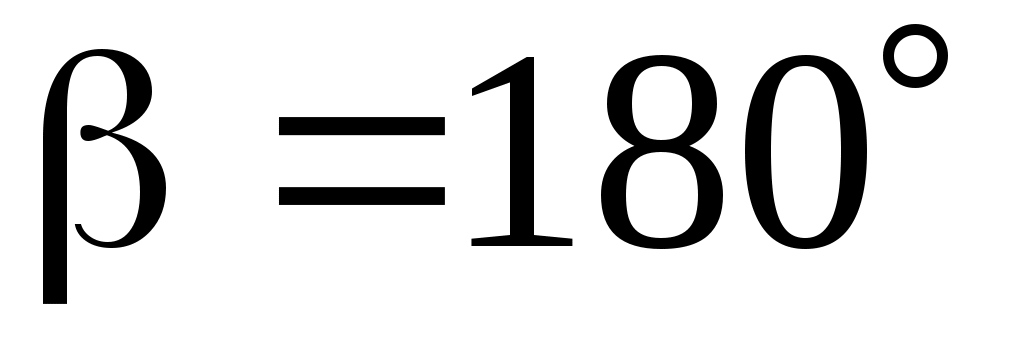 ). ).
Система состоит из стержней 1, 2, 3 и ползунов B, D; система имеет одну степень свободы.
Применим принцип возможных перемещений:
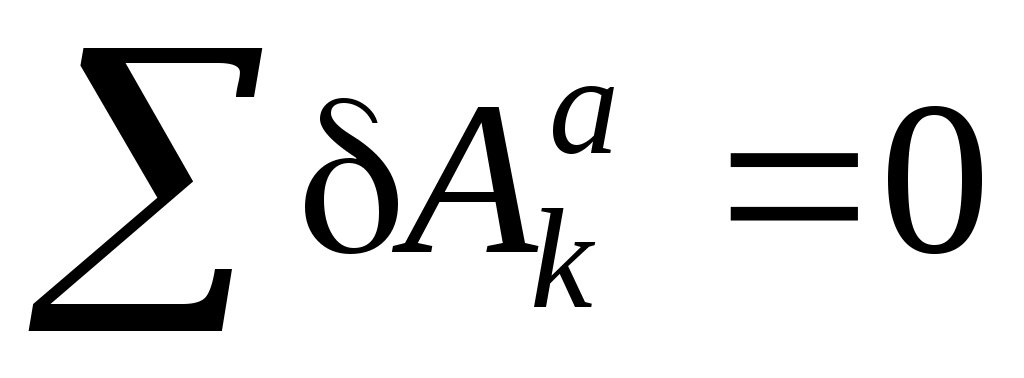 , ,
или
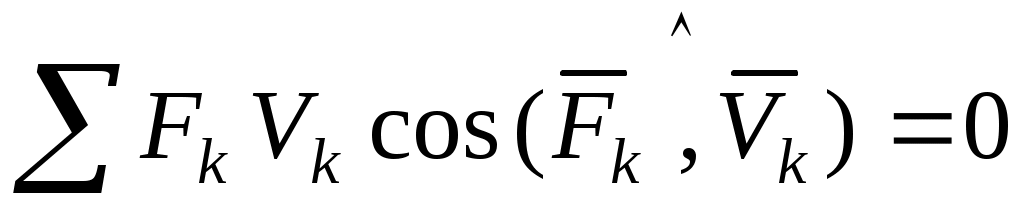 (1) (1)
(так как в задаче К4 мы уже встречались с определением скоростей точек плоского механизма).
2. Покажем на рисунке действующие на точки механизма активные силы: силу  , силу упругости , силу упругости 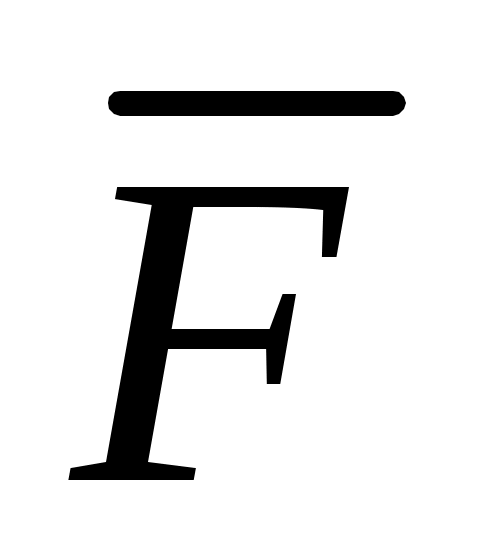 пружины (предполагая, что пружина растянута) и пару с моментом М. пружины (предполагая, что пружина растянута) и пару с моментом М.
Неизвестную силу Fнайдем с помощью уравнения (1), а зная Fи учитывая, что 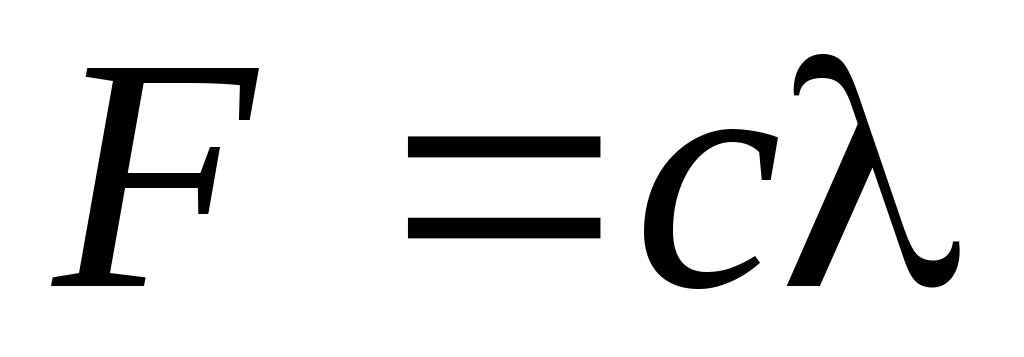 , определим . , определим .
3. Сообщим системе возможное перемещение. При этом стержень 1 приобретет угловую скорость 1, ползун B – скорость 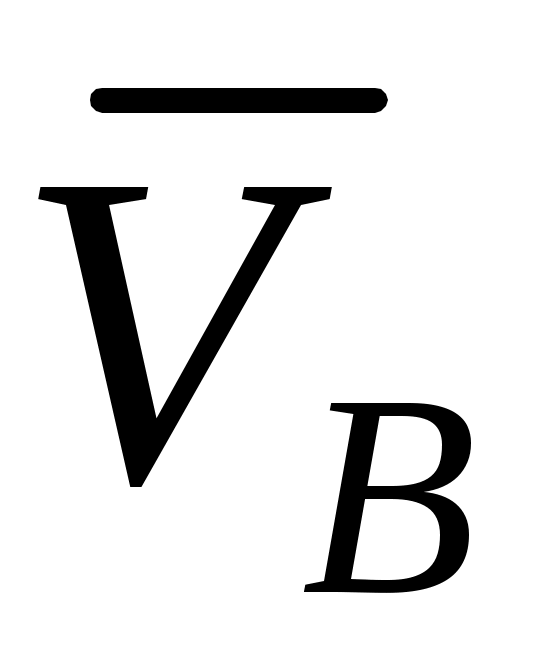 , ползун D – скорость , ползун D – скорость 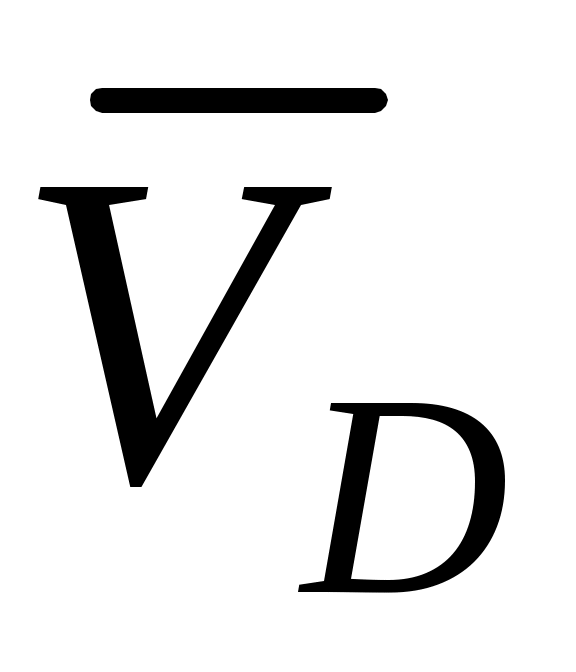 ; эти скорости потребуются при вычислении слагаемых в (1). Так как система имеет одну степень свободы, то ; эти скорости потребуются при вычислении слагаемых в (1). Так как система имеет одну степень свободы, то 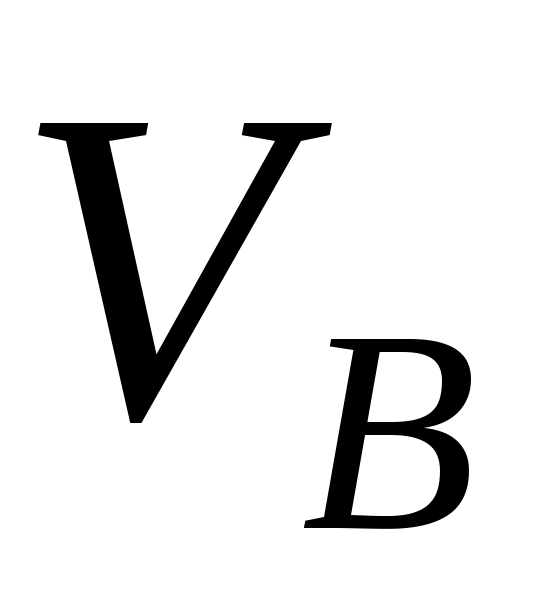 и и 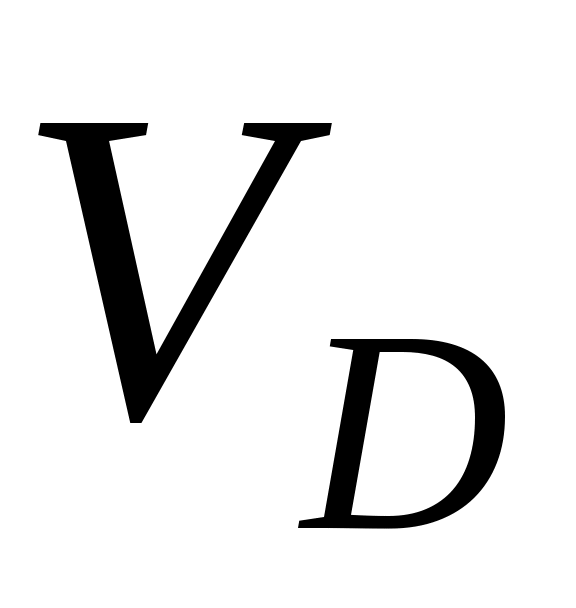 можно выразить через 1. Ход расчетов такой же, как в задаче К4. можно выразить через 1. Ход расчетов такой же, как в задаче К4.
4. Кинематическая часть задачи. Все вычисления и построения векторов проводятся для заданного положения механизма (механизм не перемещается в новое положение), так как возможные перемещения – бесконечно малые.
Сначала найдем и изобразим на рисунке скорость точки A (направление вектора скорости 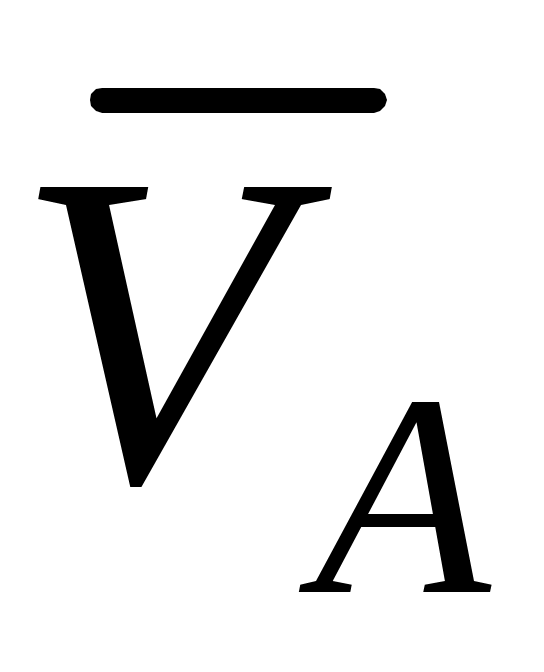 определяется направлением угловой скорости определяется направлением угловой скорости 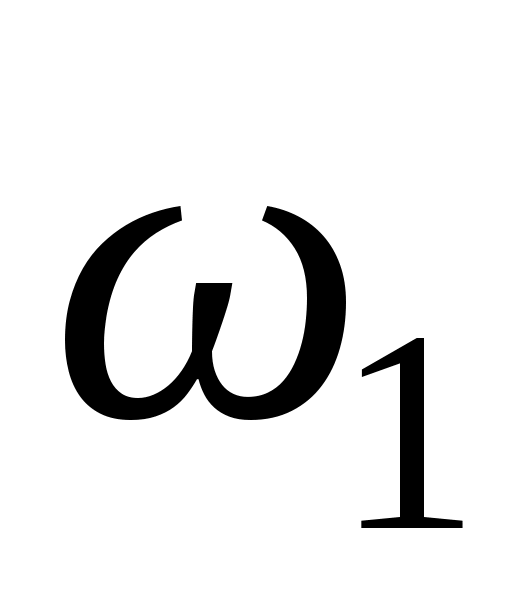 ): ):
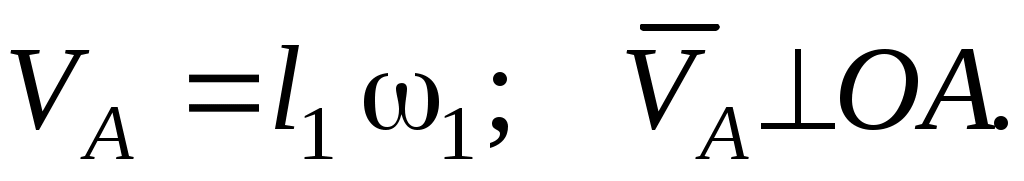
Определим и изобразим на рисунке скорость точки D. Скорость 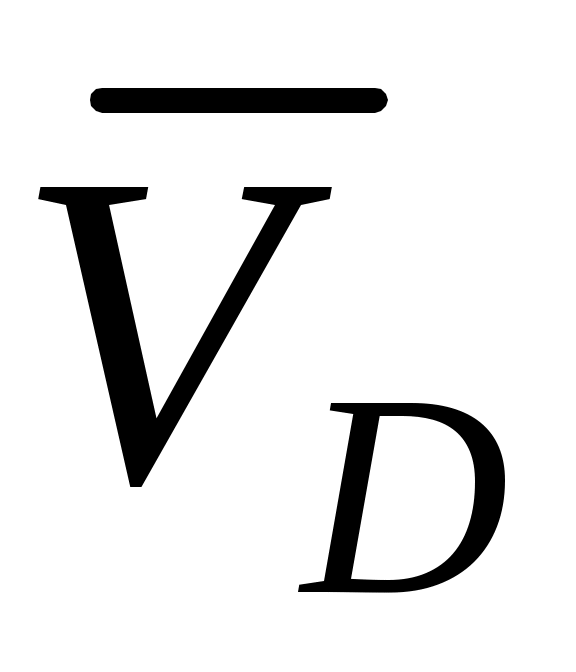 – вдоль направляющих ползуна D. По теореме о проекциях скоростей точек абсолютно твердого тела, проекции скоростей – вдоль направляющих ползуна D. По теореме о проекциях скоростей точек абсолютно твердого тела, проекции скоростей 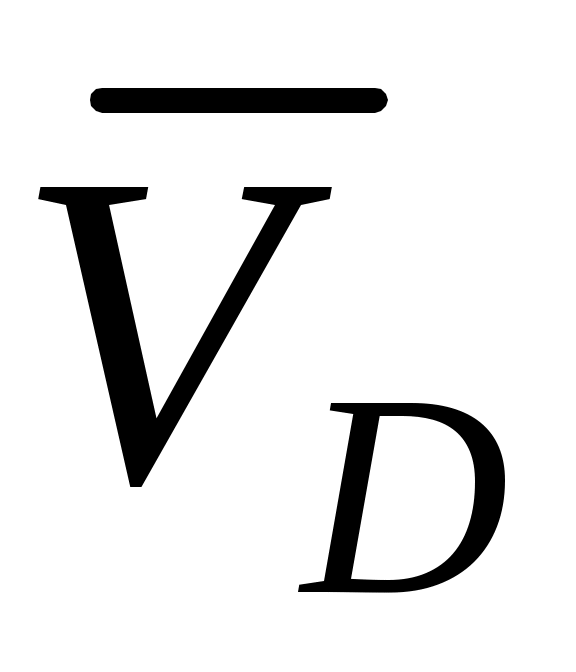 и и 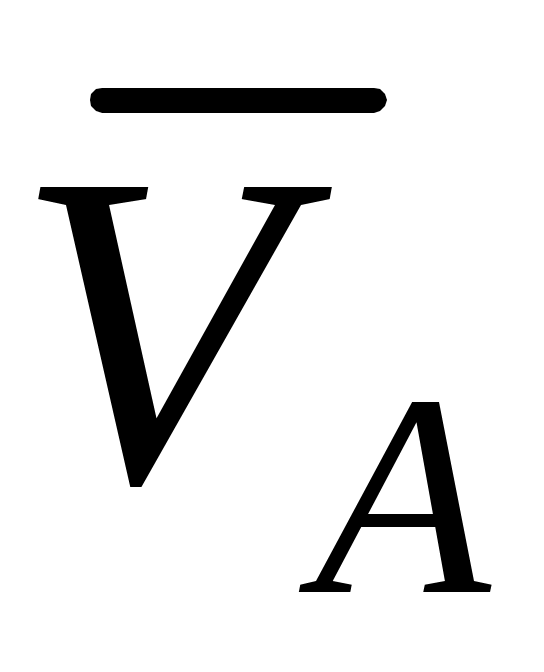 на прямую ADалгебраически равны (имеют одинаковые модули и знаки): на прямую ADалгебраически равны (имеют одинаковые модули и знаки):
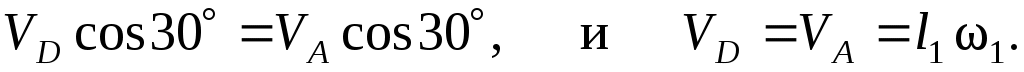 (2) (2)
Чтобы определить скорость точки 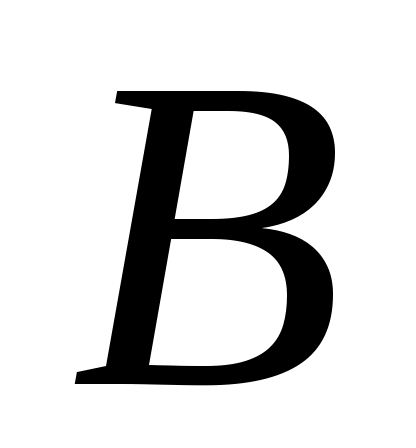 , найдем сначала скорость точки , найдем сначала скорость точки 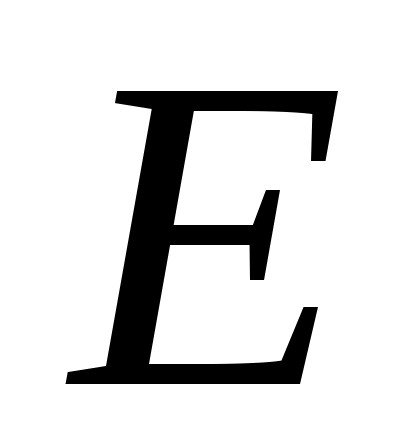 . Для этого построим мгновенный центр скоростей С2стержня 2. Он находится на пересечении перпендикуляров к векторам . Для этого построим мгновенный центр скоростей С2стержня 2. Он находится на пересечении перпендикуляров к векторам 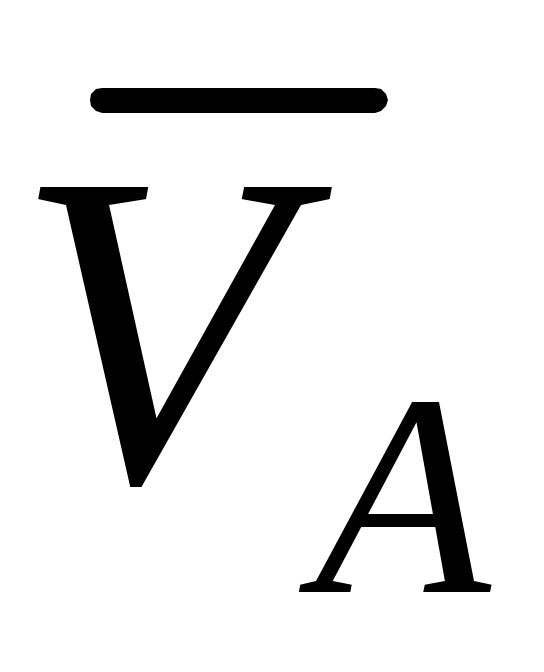 и и 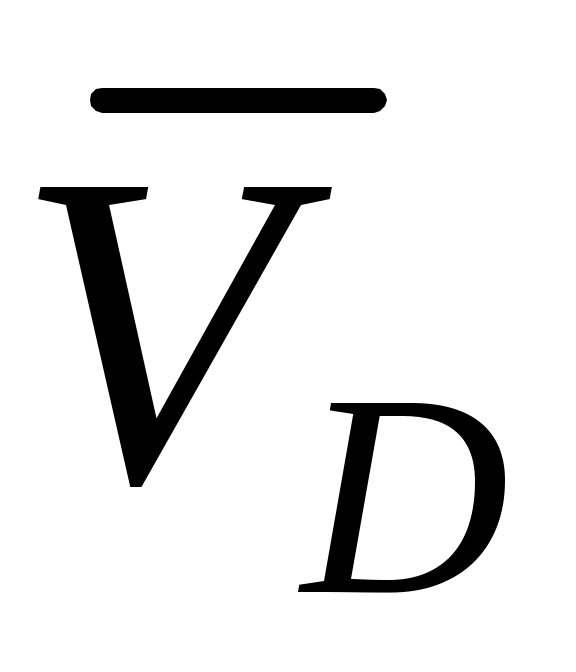 , восставленных из точек А и D.Покажем направление мгновенного поворота стержня 2 (вокруг С2),учитывая направление , восставленных из точек А и D.Покажем направление мгновенного поворота стержня 2 (вокруг С2),учитывая направление 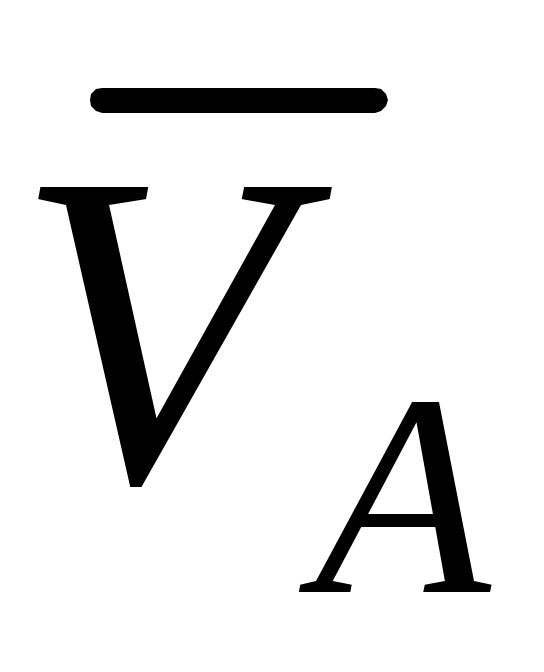 или или 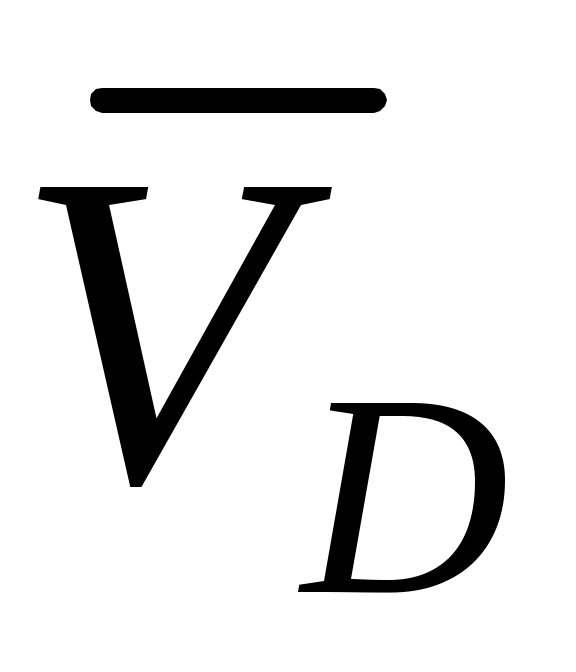 . Так как . Так как 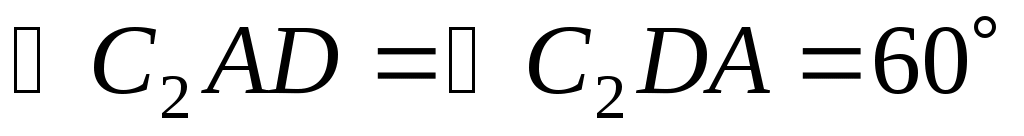 , то , то 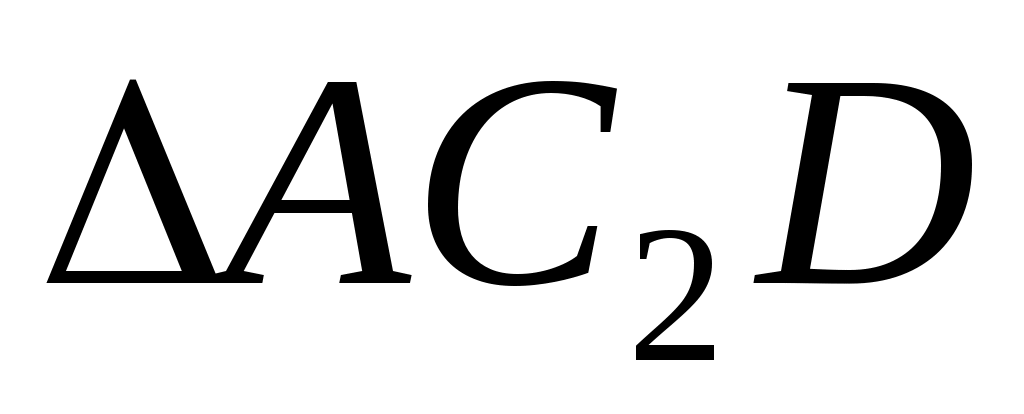 – равносторонний и С2Е в нем высота, поскольку АЕ = ED. Тогда скорость – равносторонний и С2Е в нем высота, поскольку АЕ = ED. Тогда скорость 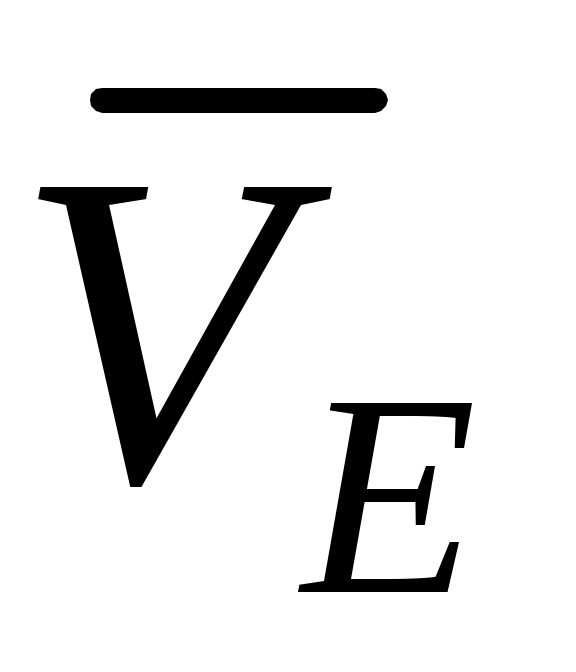 , перпендикулярная С2Е,будет направлена по прямой ЕА (при изображении , перпендикулярная С2Е,будет направлена по прямой ЕА (при изображении 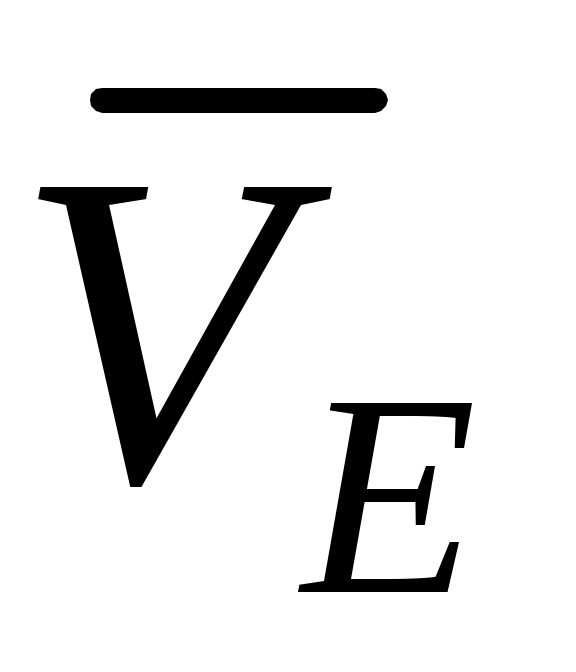 учитываем направление мгновенного поворота стержня 2). учитываем направление мгновенного поворота стержня 2).
Воспользовавшись опять теоремой о проекциях скоростей точек E и A на прямую EA, получим
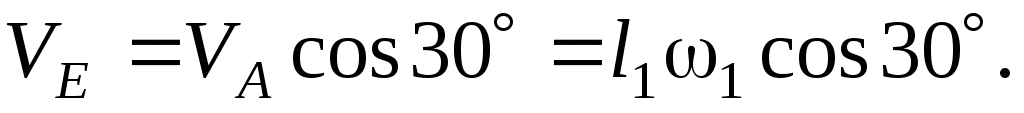
Значение скорости 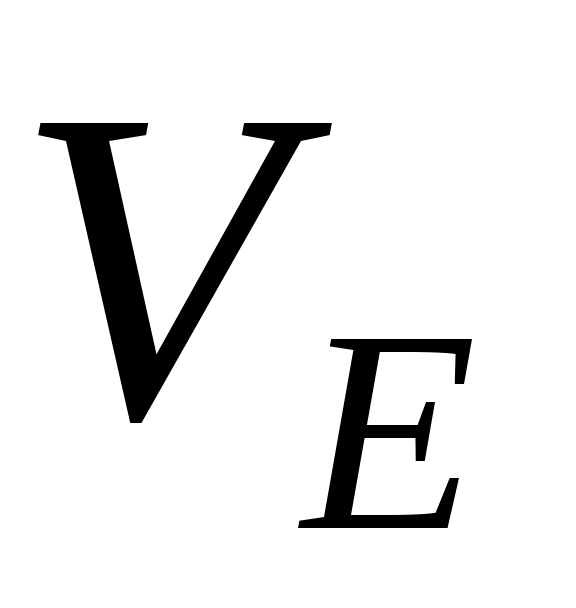 можно найти и другим способом, составив пропорцию можно найти и другим способом, составив пропорцию
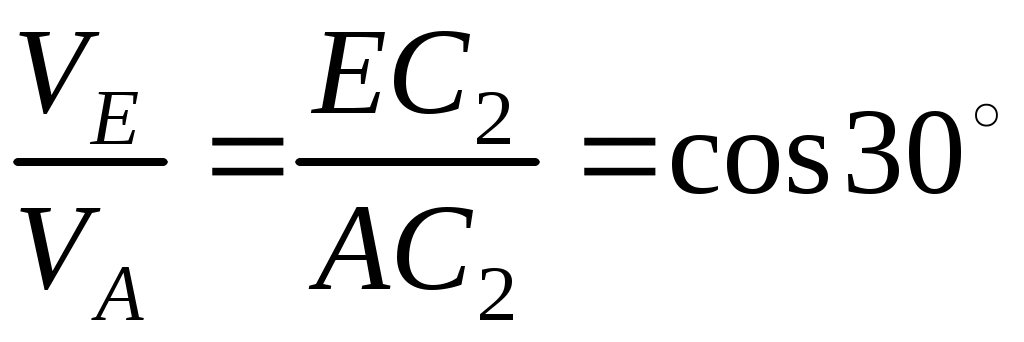 . .
Находим 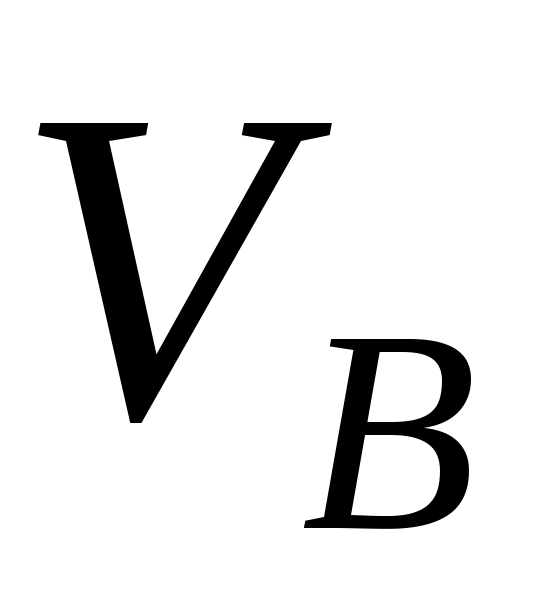 , применив еще раз теорему о проекциях скоростей , применив еще раз теорему о проекциях скоростей 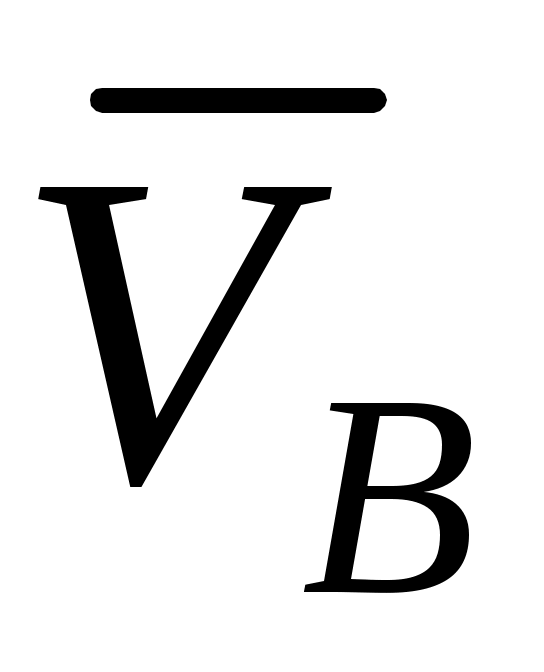 и и 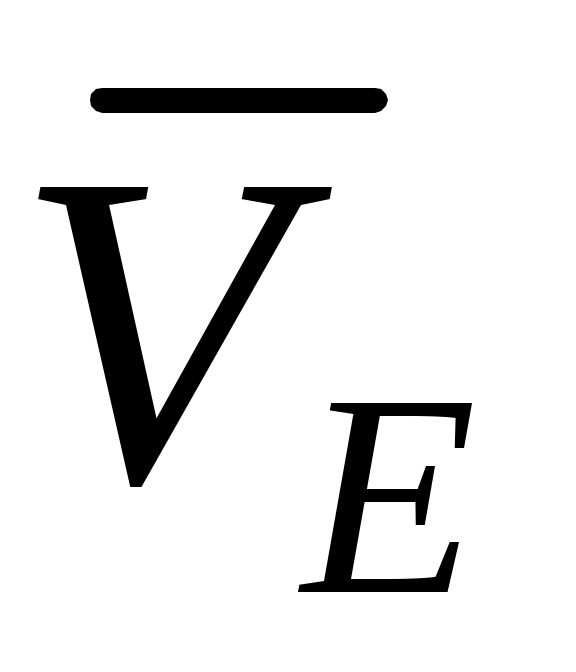 на прямую BE и учитывая, что на прямую BE и учитывая, что 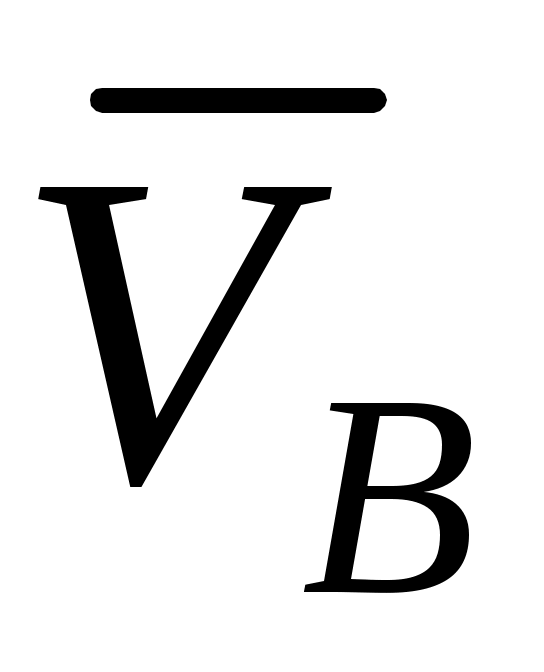 параллельна направляющим ползуна B. параллельна направляющим ползуна B.
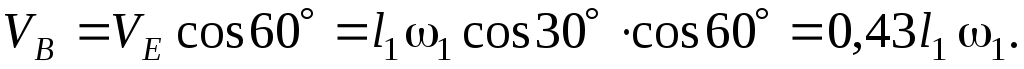
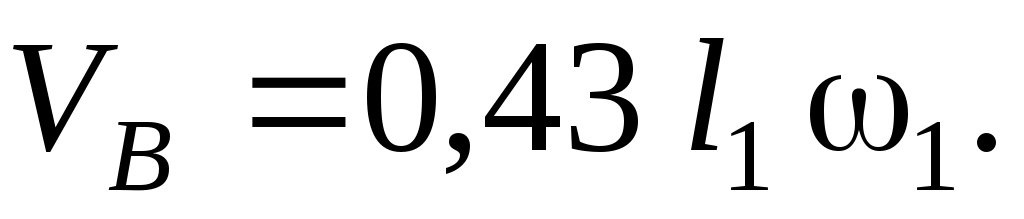 (3) (3)
Изображаем 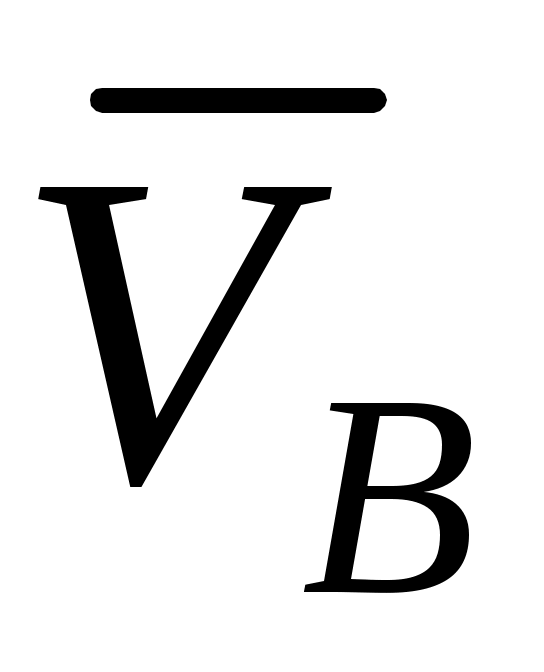 на рисунке. на рисунке.
5. Составим уравнение (1) для показанных на рисунке сил и скоростей.
Мощность силы  : : 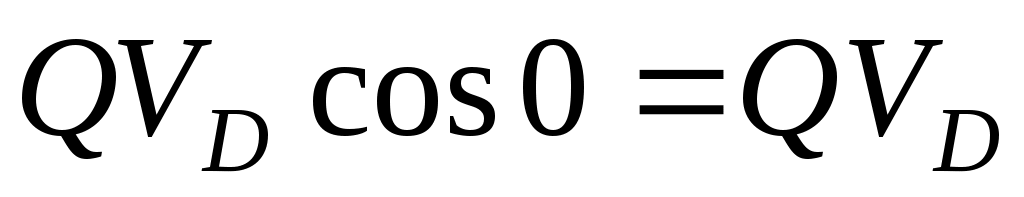 . .
Мощность силы 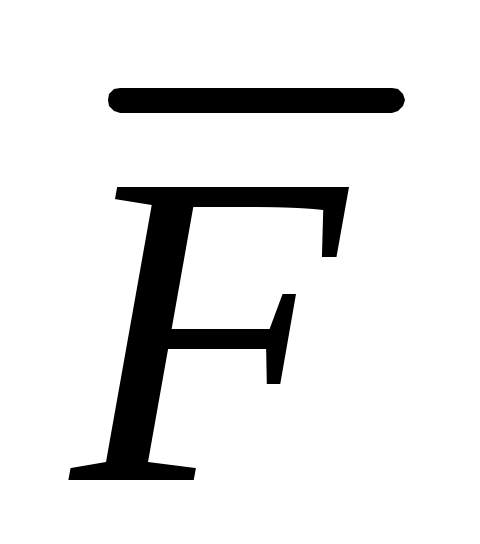 : : 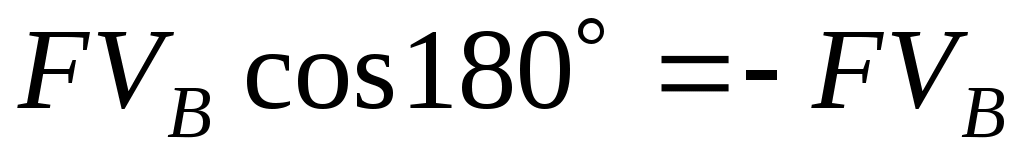 . .
Мощность пары сил: 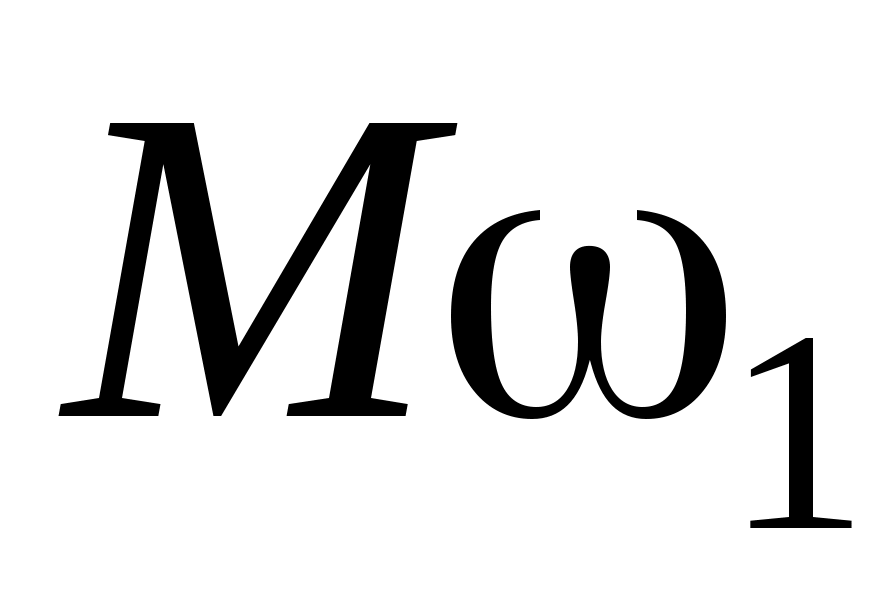 , так как элементарная работа пары (см. задачу Д3) , так как элементарная работа пары (см. задачу Д3) 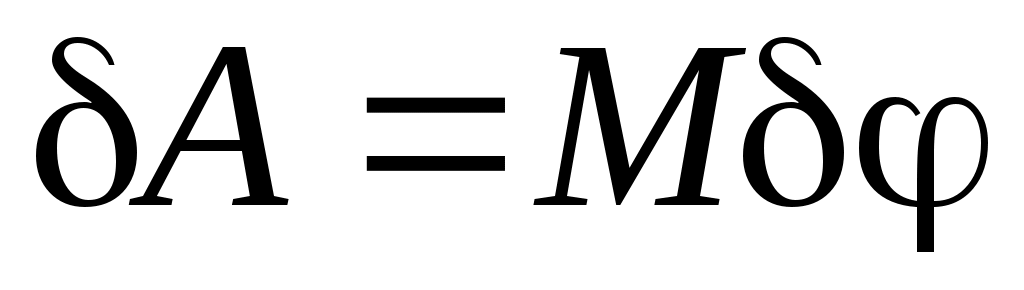 , а мощность равна , а мощность равна 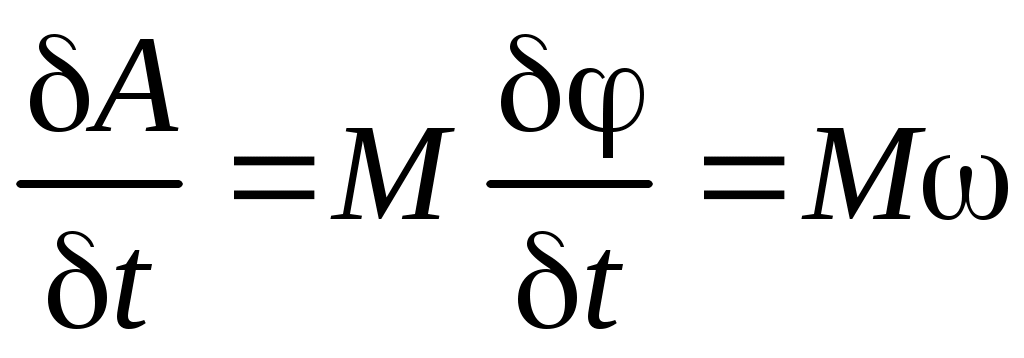 . .
В итоге, уравнение (1) принимает вид
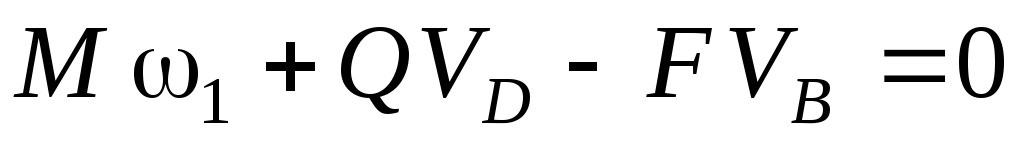 . .
Заменяя здесь 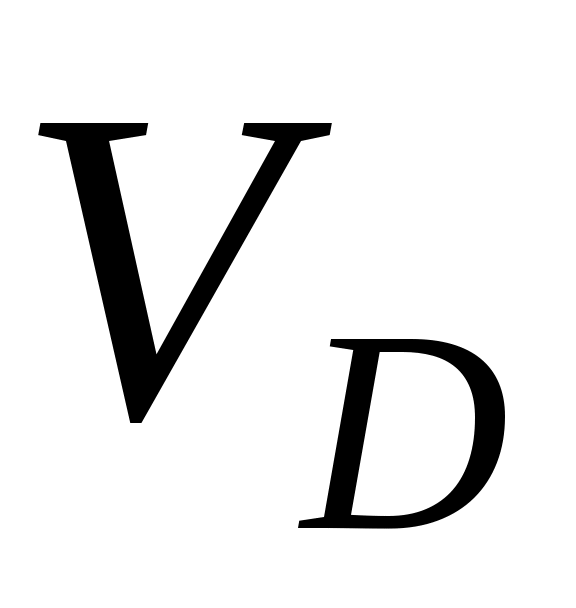 и и 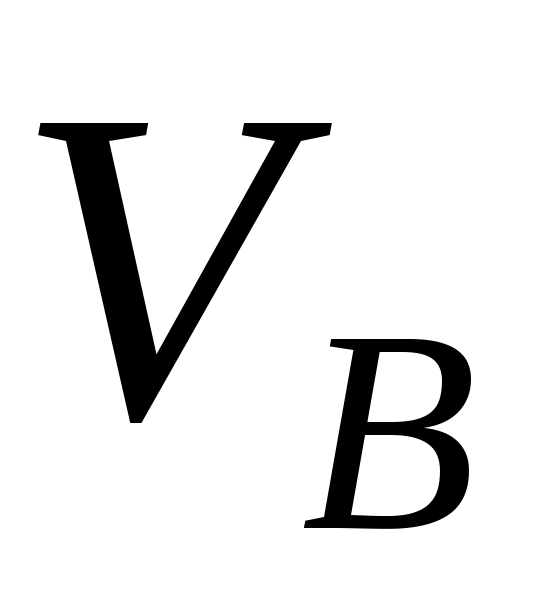 их значениями (2) и (3) и вынося их значениями (2) и (3) и вынося 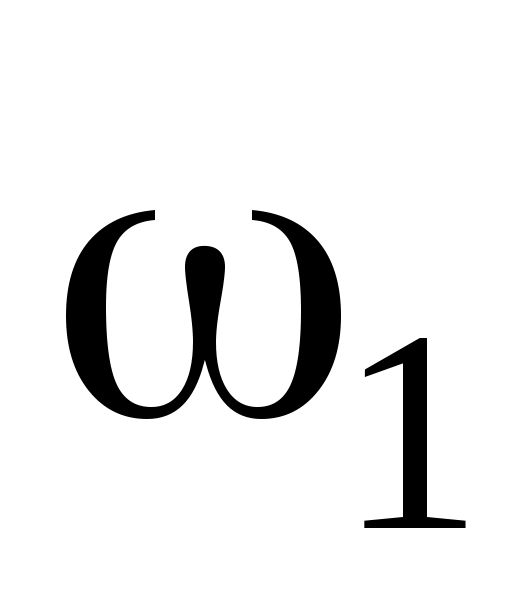 за скобки, получаем за скобки, получаем
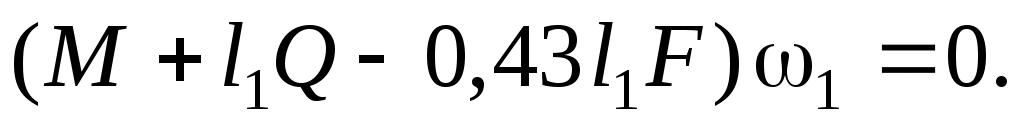 (4) (4)
Так как равенство (4) выполняется при любой возможной угловой скорости 1, то
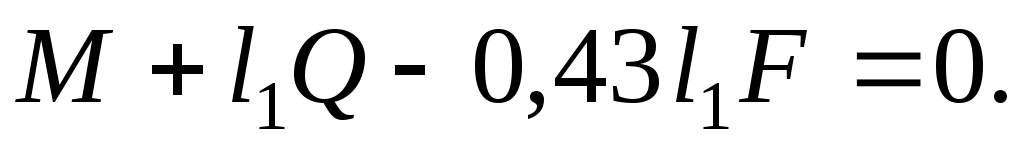 (5) (5)
Из уравнения (5) находим значение силы упругости 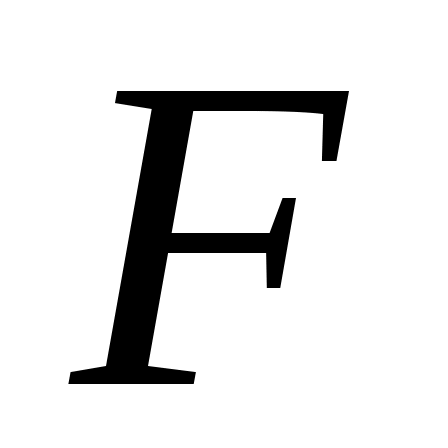 и определяем деформацию пружины и определяем деформацию пружины 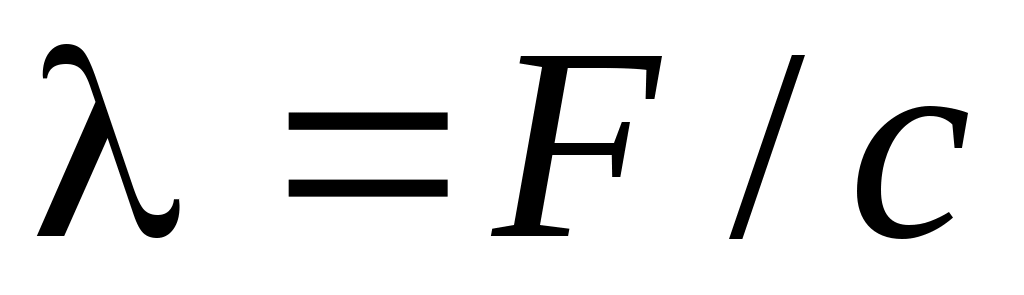 . .
Ответ: = 13,5 см. Знак указывает, что пружина, как и предполагалось, растянута.
Задача Д6
(тема: “Принцип Даламбера для механической системы”)
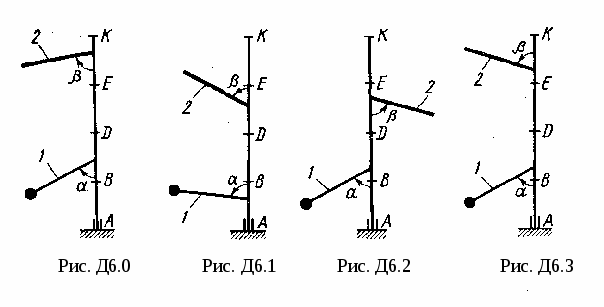
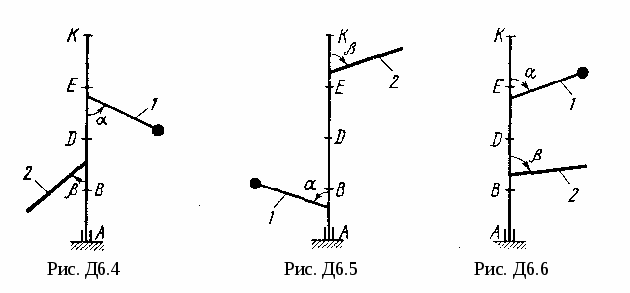
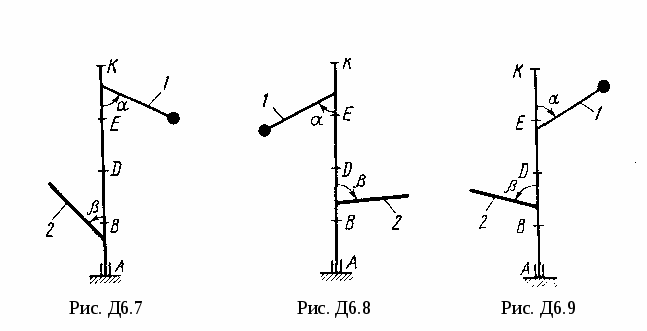
Вертикальный вал 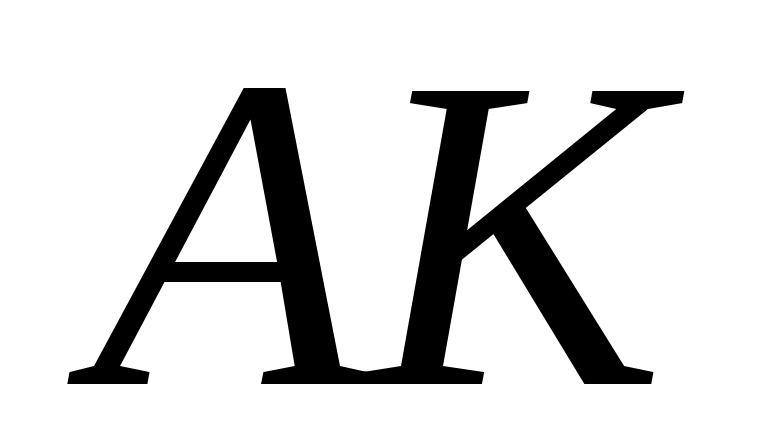 (рис. Д6.0-Д6.9, табл. Д6), вращается с постоянной угловой скоростью (рис. Д6.0-Д6.9, табл. Д6), вращается с постоянной угловой скоростью 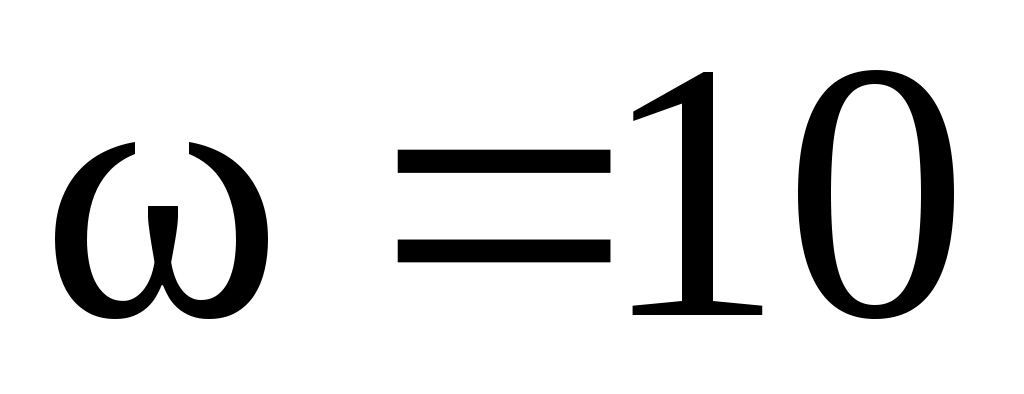 с-1. Вал имеет две опоры: подпятник в точке А и цилиндрический подшипник в точке, указанной в табл. Д6 ( с-1. Вал имеет две опоры: подпятник в точке А и цилиндрический подшипник в точке, указанной в табл. Д6 (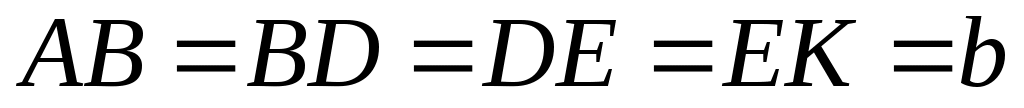 ). К валу жестко прикреплены невесомый стержень 1 длиной ). К валу жестко прикреплены невесомый стержень 1 длиной 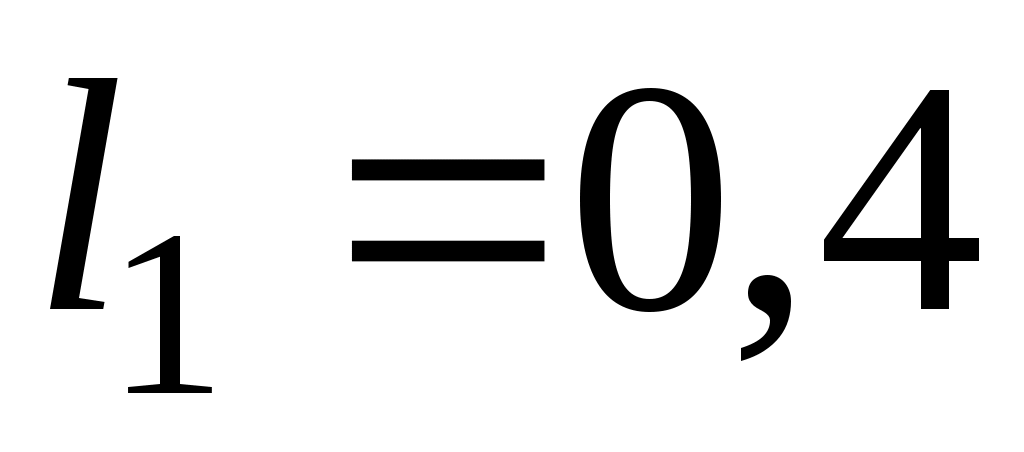 м с точечной массой м с точечной массой 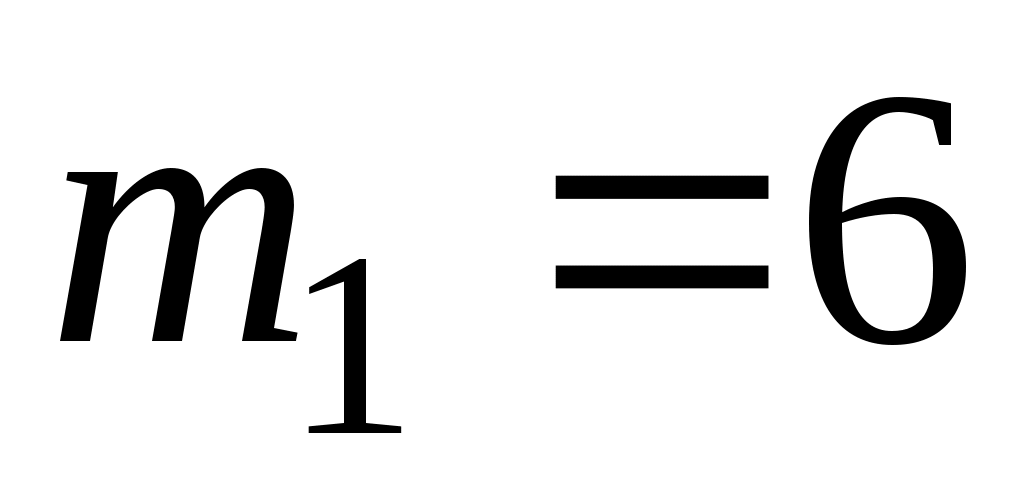 кг на конце и однородный стержень 2 длиной кг на конце и однородный стержень 2 длиной 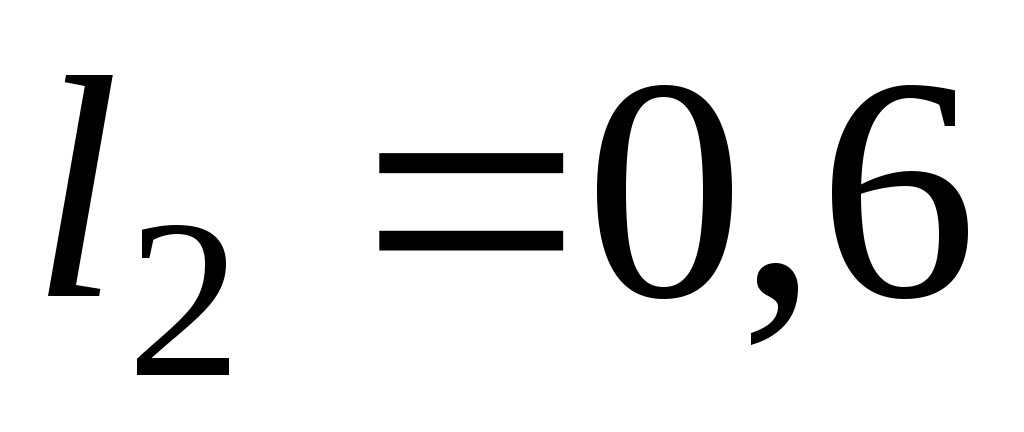 м, имеющий массу м, имеющий массу 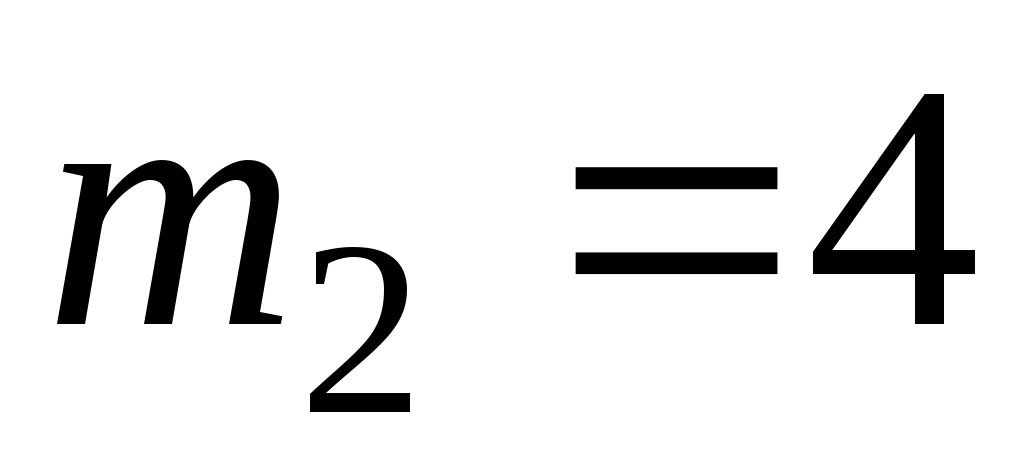 кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу и углы α и β указаны в таблице. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу и углы α и β указаны в таблице. Пренебрегая весом вала, определить реакции подпятника и подшипника. При окончательных подсчетах принять 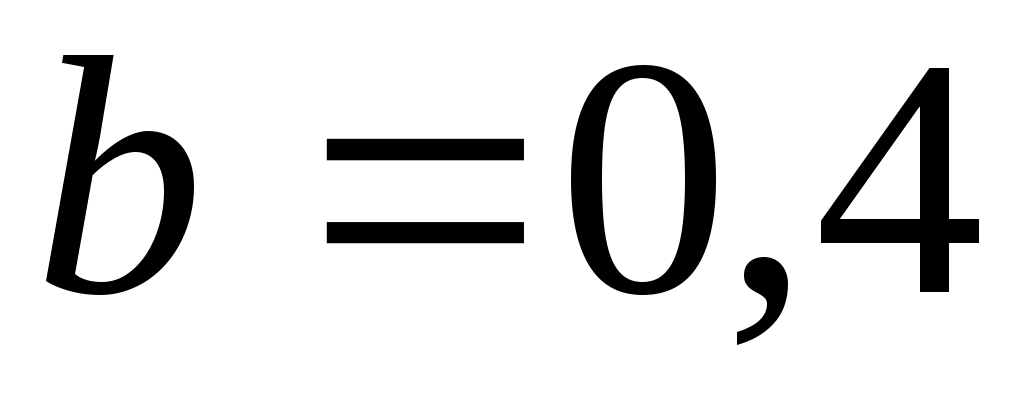 м. м.
Перед выполнением задания прочтите по учебнику тему: «Принцип Даламбера». Ответьте на вопросы:
Сформулируйте принцип Даламбера для точки.
Как определяется модуль и направление силы инерции для точки? В каких случаях сила инерции равна нулю?
Сформулируйте принцип Даламбера для системы.
Чему равны главный вектор и главный момент сил инерции системы?
Запишите уравнения равновесия произвольной системы сил и плоской системы сил в координатной форме (вспомнив соответствующие уравнения статики).
(краткие сведения из теории)
Принцип Даламбера для точки. Рассмотрим дифференциальное уравнение движения точки в инерциальной системе отсчета в векторной форме:
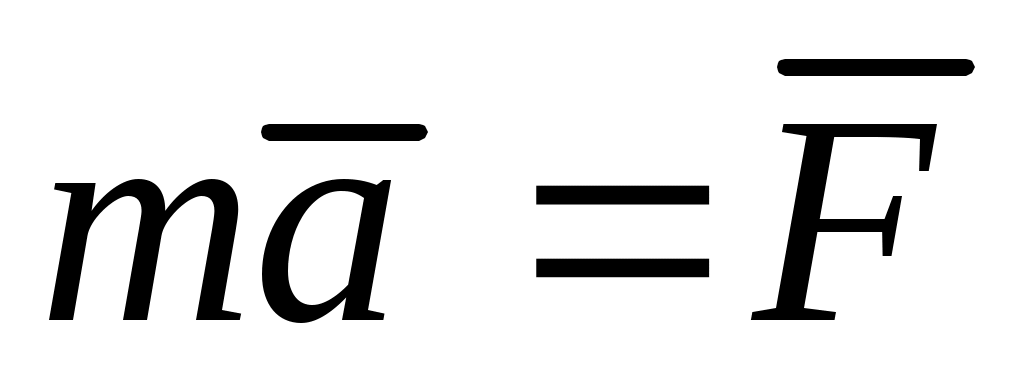 , (1) , (1)
где 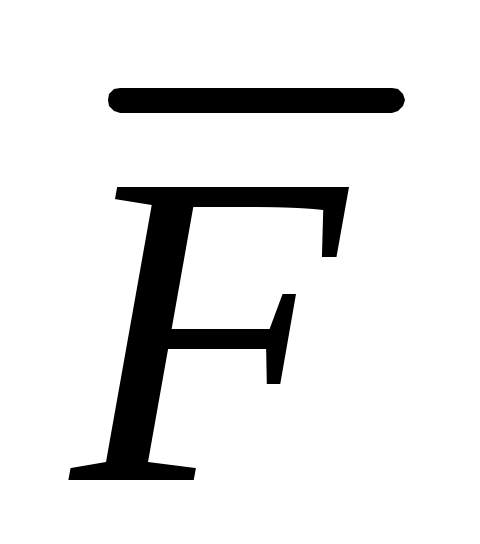 – векторная сумма всех сил, действующих на точку (активных и реакций связей). Перенесем вектор – векторная сумма всех сил, действующих на точку (активных и реакций связей). Перенесем вектор 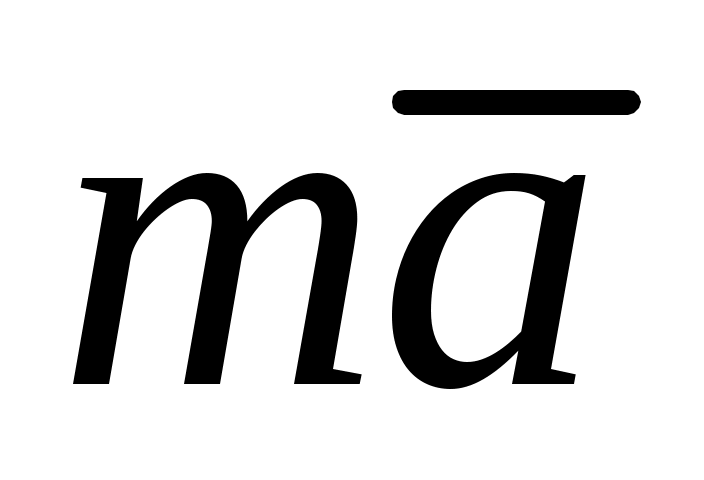 в правую часть уравнения (1): в правую часть уравнения (1): 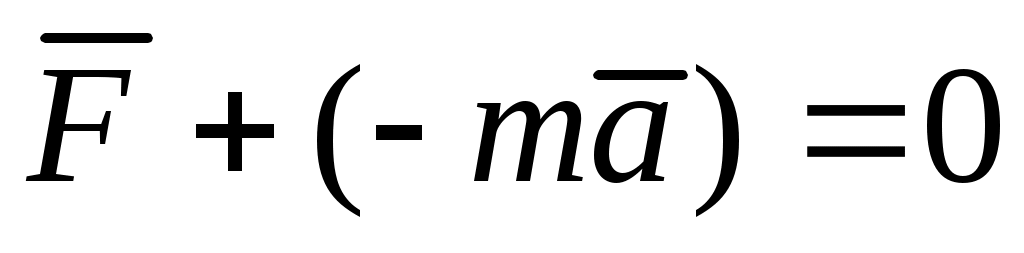 ; обозначим ; обозначим 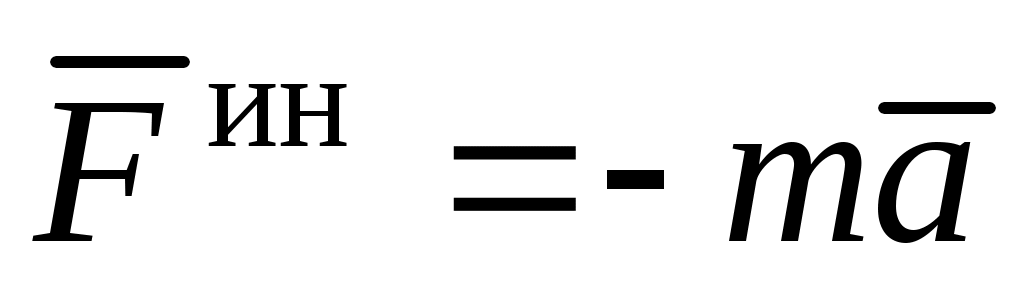 ; тогда получим уравнение ; тогда получим уравнение
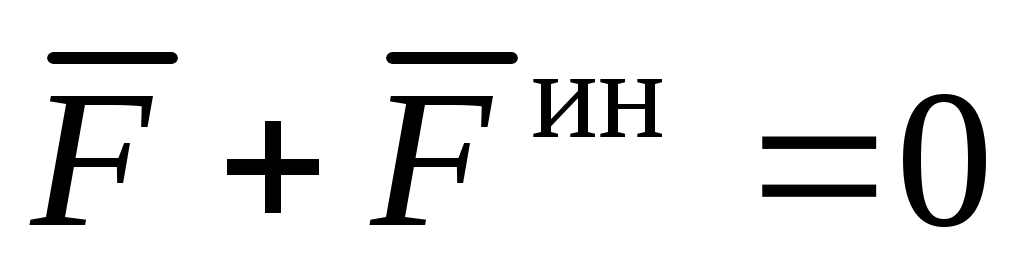 , (2) , (2)
где
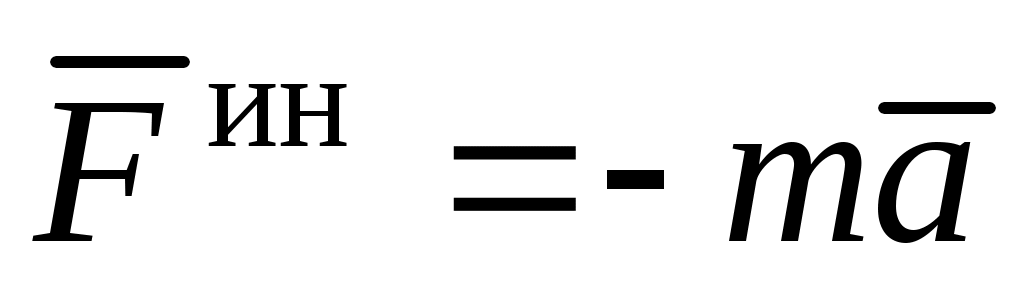 ; (3) ; (3)
эта величина называется силой инерции точки.
Уравнение (2) по форме соответствует уравнению равновесия сил в векторной форме. В этом и состоит принцип Даламбера для точки: если к приложенным к точке силам добавить силу инерции (3), то полученная система сил (активных, реакций связей и сил инерции) будет уравновешенной и задачу динамики можно решать, применив методы статики.
Такой метод решения задач динамики называется методом кинетостатики.
|
Сила инерции точки 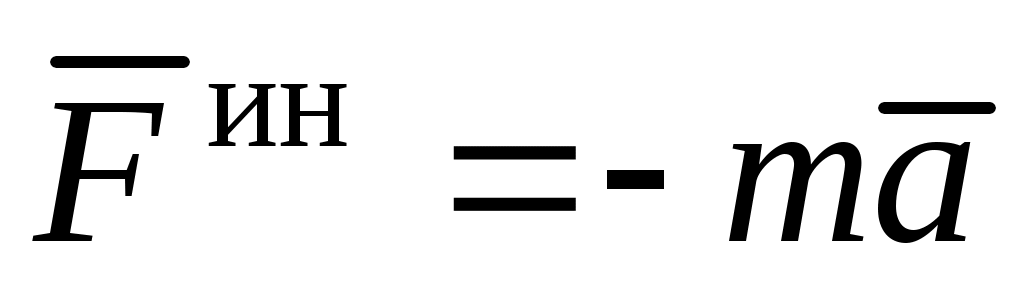 (см. (3)). Модуль силы инерции точки равен (см. (3)). Модуль силы инерции точки равен 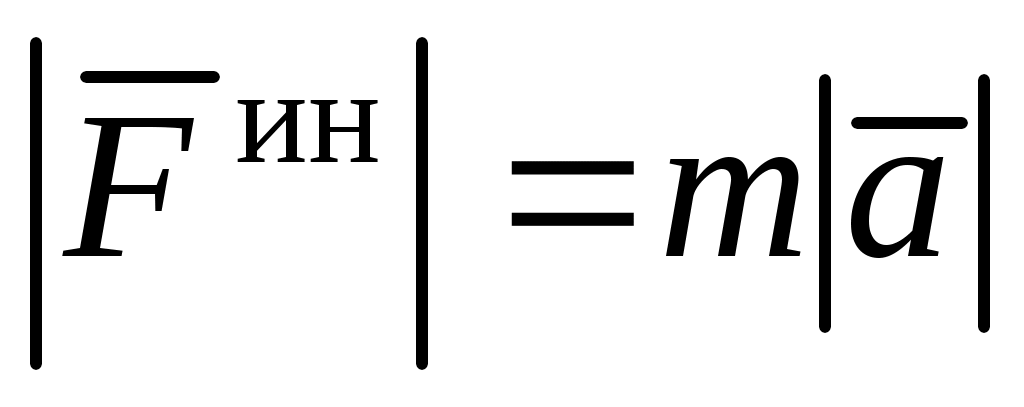 ; направлена сила инерции ; направлена сила инерции 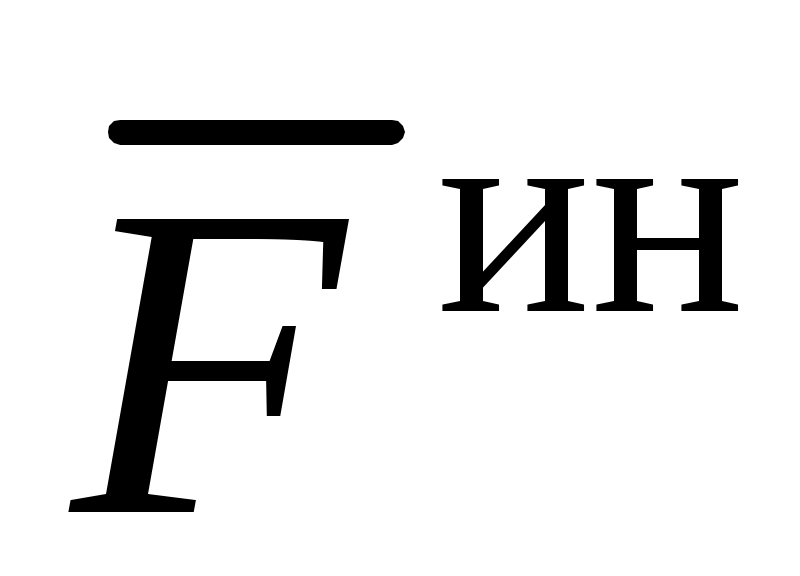 в сторону, противоположную абсолютному ускорению точки в сторону, противоположную абсолютному ускорению точки  . Поэтому для построения . Поэтому для построения 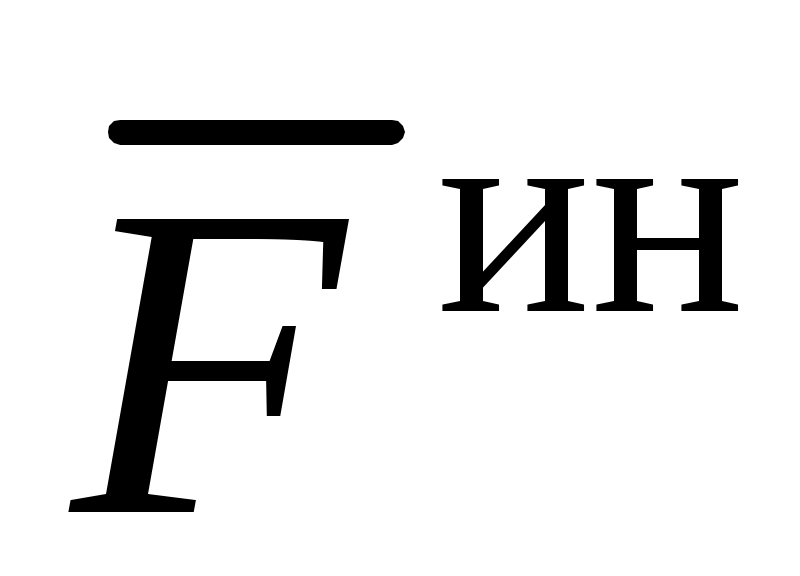 на рисунке следует сначала построить вектор на рисунке следует сначала построить вектор  (или его составляющие, например, (или его составляющие, например, 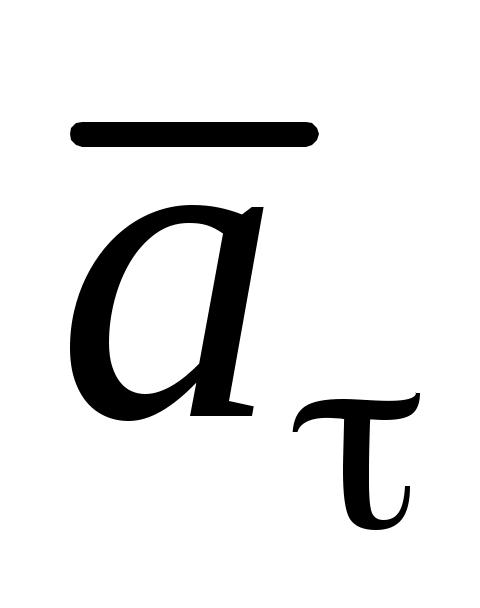 и и 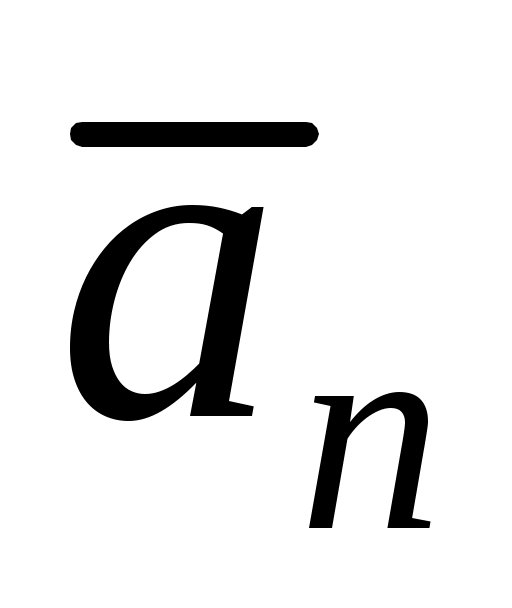 ), и затем построить ), и затем построить 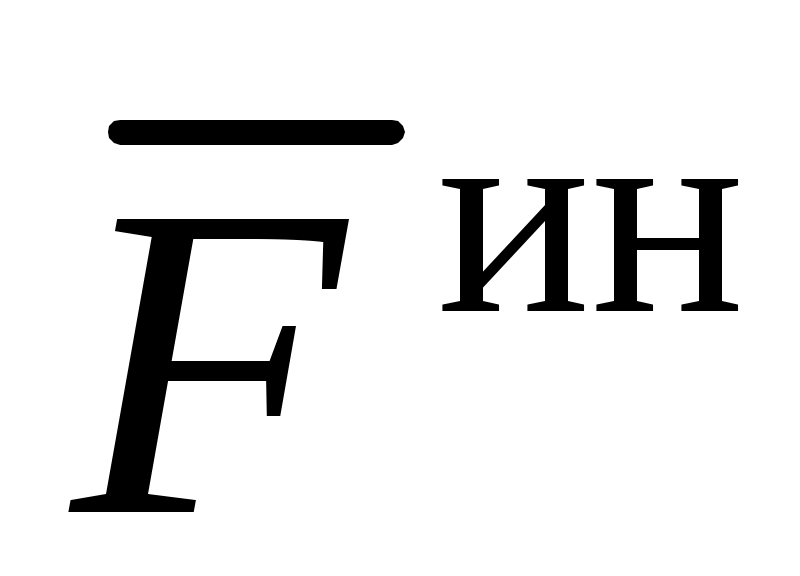 в сторону, противоположную вектору в сторону, противоположную вектору  (или (или 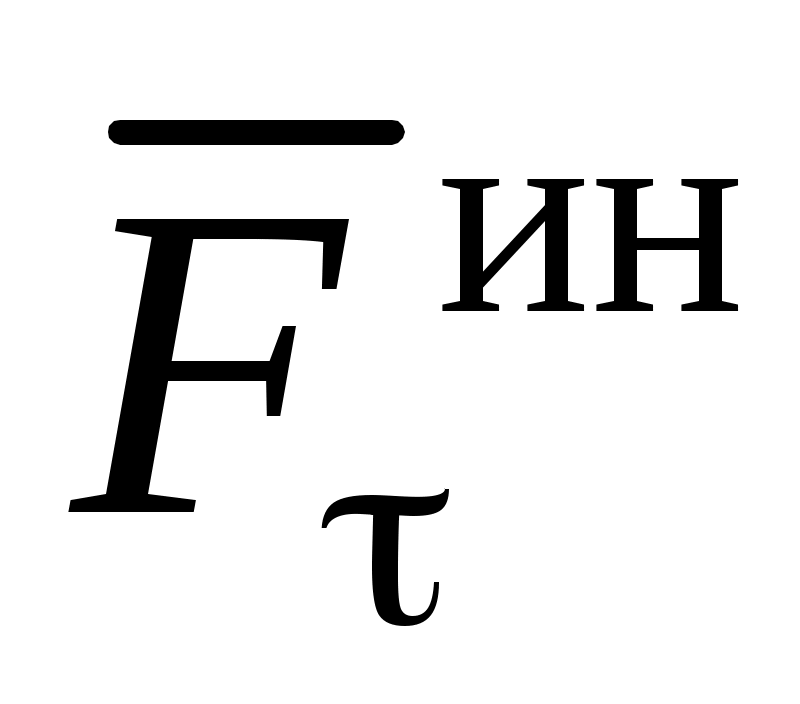 и и 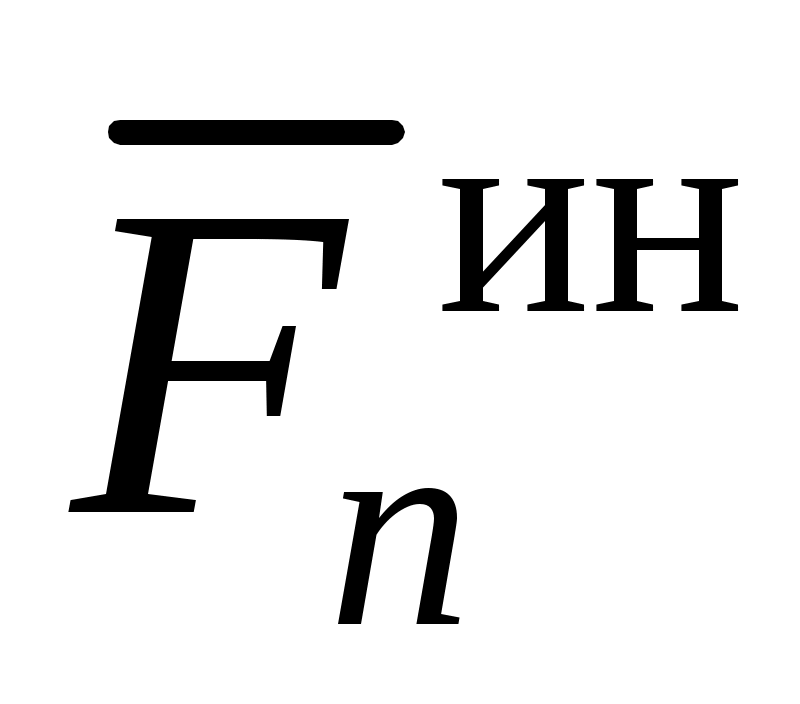 в стороны, противоположные в стороны, противоположные 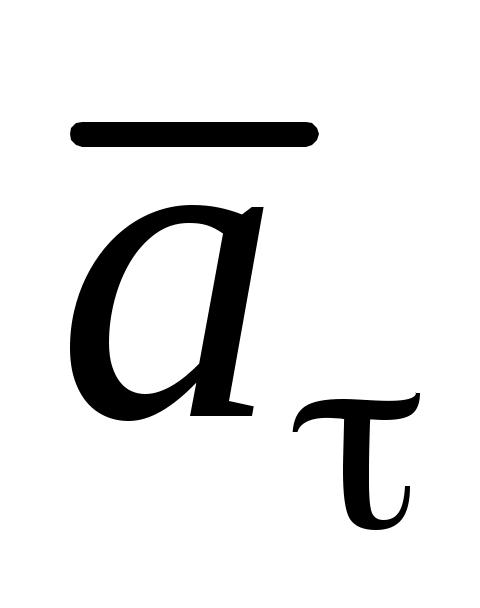 и и 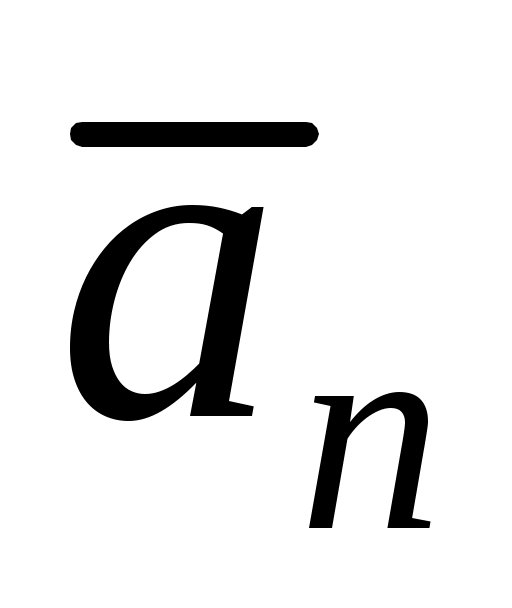 , соответственно). , соответственно).
Принцип Даламбера для системы. Применим описанный выше принцип Даламбера к каждой точке системы. К силам, действующим на каждую точку (внешним и внутренним), добавляется сила инерции (3). Получаем систему сил (внешних, внутренних и сил инерции) для всех точек системы.
Принцип Даламбера для системы формулируется следующим образом: если к внешним силам (активным и реакциям связей), действующим на каждую точку системы, добавить силу инерции (3), то полученная система сил будет уравновешенной и для нее справедливы уравнения статики.
Уравнения равновесия сил (внешних (активных и реакций связей) и сил инерции) в векторной форме:
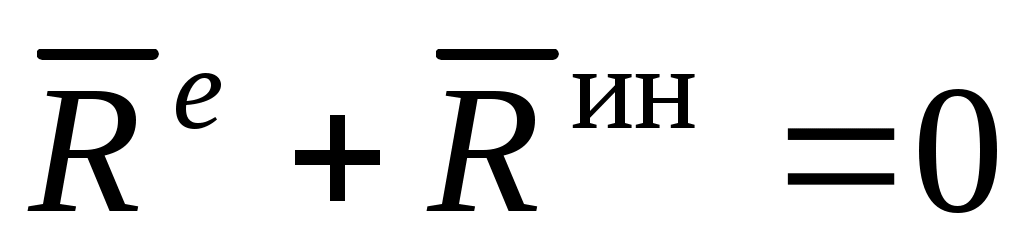 ; ;
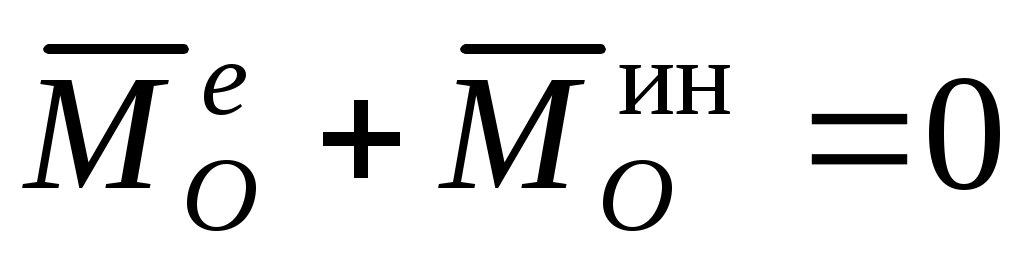 , ,
где 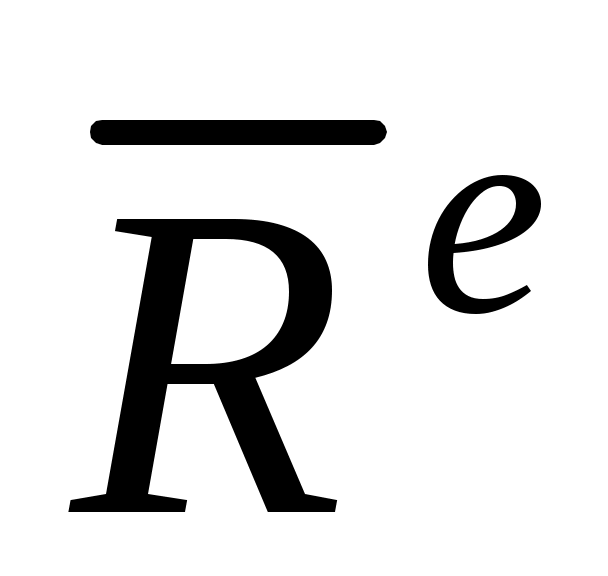 , , 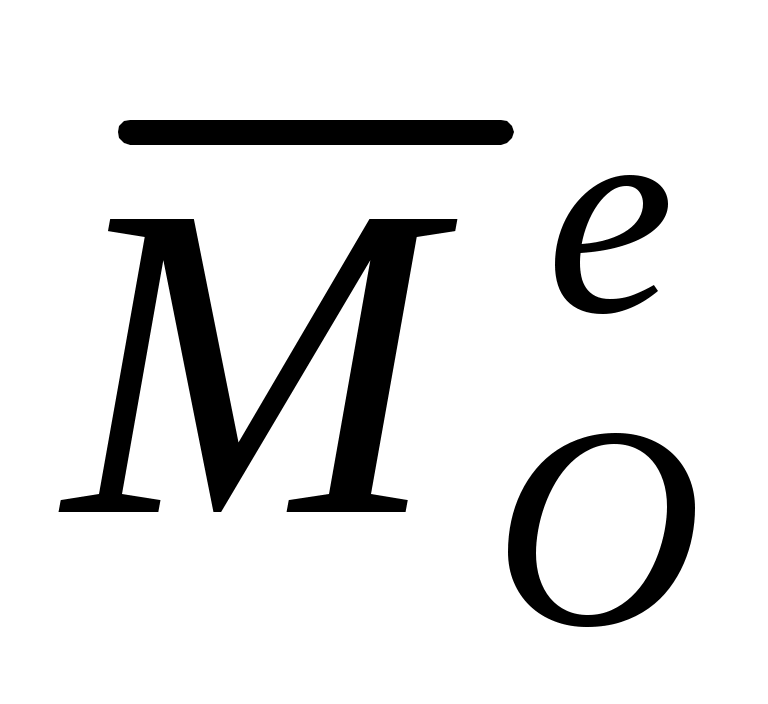 – главный вектор и главный момент относительно произвольного центра O внешних сил (активных и реакций связей); – главный вектор и главный момент относительно произвольного центра O внешних сил (активных и реакций связей); 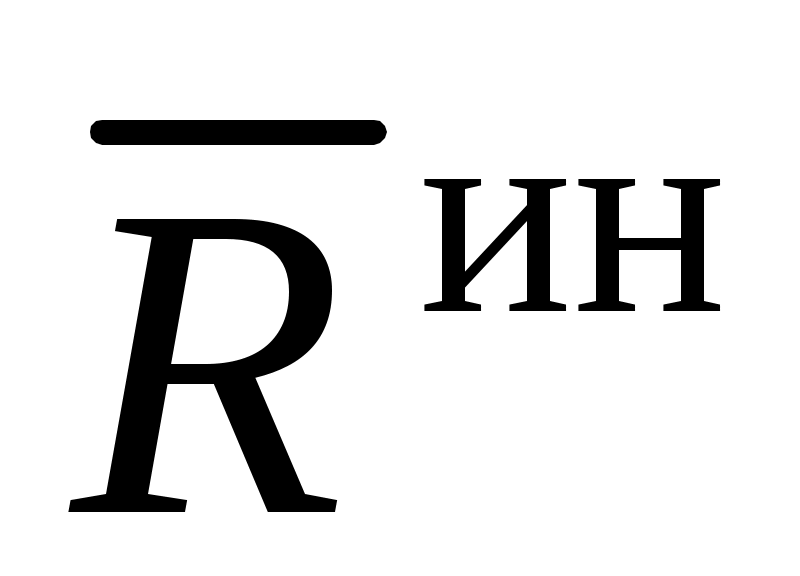 , , 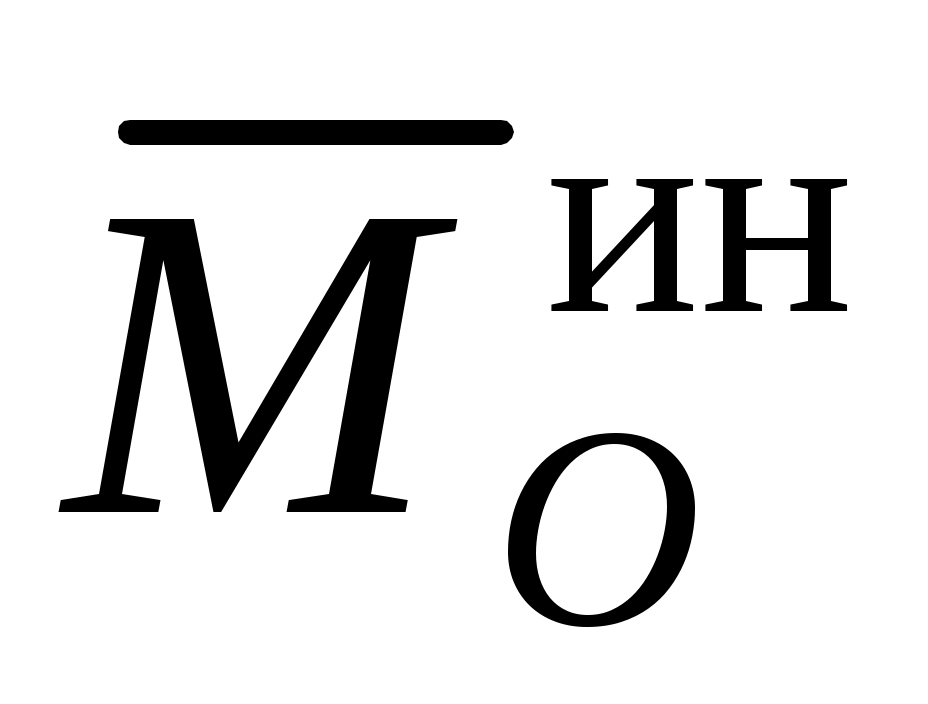 – главный вектор и главный момент относительно произвольного центра O сил инерции. В алгебраической (координатной) форме уравнения равновесия записываются различным образом, в зависимости от типа получившейся системы сил (произвольная система сил, плоская система сил и т. д., см. раздел “Статика”). – главный вектор и главный момент относительно произвольного центра O сил инерции. В алгебраической (координатной) форме уравнения равновесия записываются различным образом, в зависимости от типа получившейся системы сил (произвольная система сил, плоская система сил и т. д., см. раздел “Статика”).
Главный вектор сил инерции не зависит от центра приведения и может быть вычислен заранее:
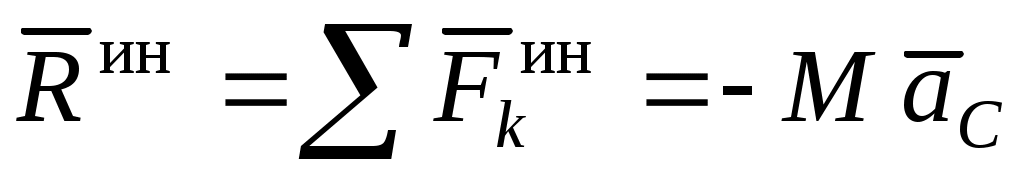 , ,
где M – масса тела (системы), 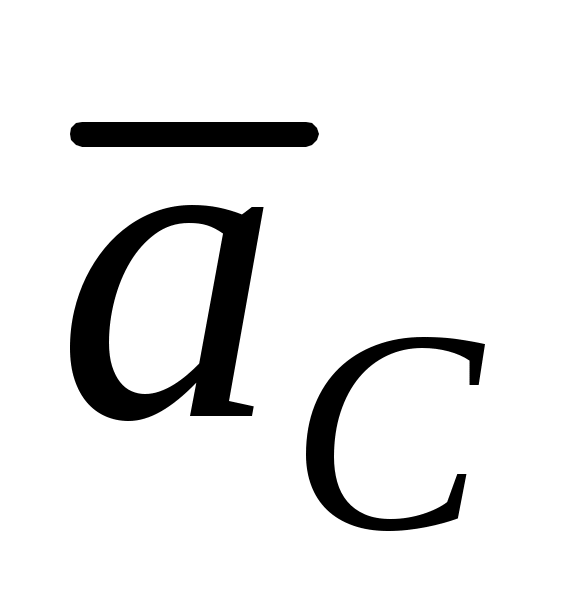 – абсолютное ускорение центра масс тела (системы). Главный вектор не обязательно приложен в центре масс (так как центр приведения – произвольная точка). – абсолютное ускорение центра масс тела (системы). Главный вектор не обязательно приложен в центре масс (так как центр приведения – произвольная точка).
Главный момент сил инерции относительно центра приведения O:
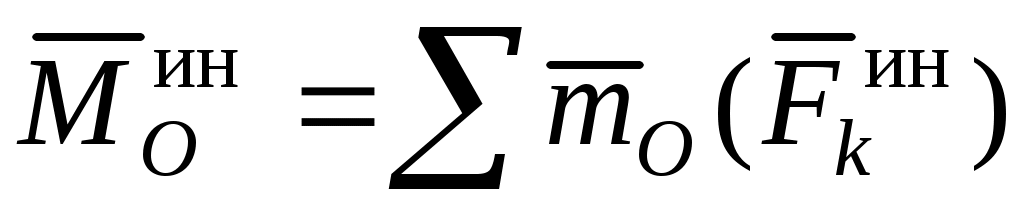 . .
Главный момент зависит от центра приведения O и заранее может быть вычислен только в некоторых частных случаях (для некоторых видов движения тела и различных центров приведения).
|
|
Рис. Д6.4
Рис. Д6.5
Рис. Д6.6
Рис. Д6.0
Рис. Д6.1
Рис. Д6.2
Рис. Д6.3
|
Рис. Д6.7
Рис. Д6.8
Рис. Д6.9
|
|
|
|
 Скачать 1.07 Mb.
Скачать 1.07 Mb.



