Методическое пособие с задачами - Динамика. Методическое пособие для студентов очнозаочной формы обучения Издание второе, исправленное и дополненное Направления (специальности)

Название	Методическое пособие для студентов очнозаочной формы обучения Издание второе, исправленное и дополненное Направления (специальности)
Дата	18.08.2021
Размер	1.07 Mb.
Формат файла
Имя файла	Методическое пособие с задачами - Динамика.doc
Тип	Методическое пособие #227221
страница	2 из 6

1 2 3 4 5 6

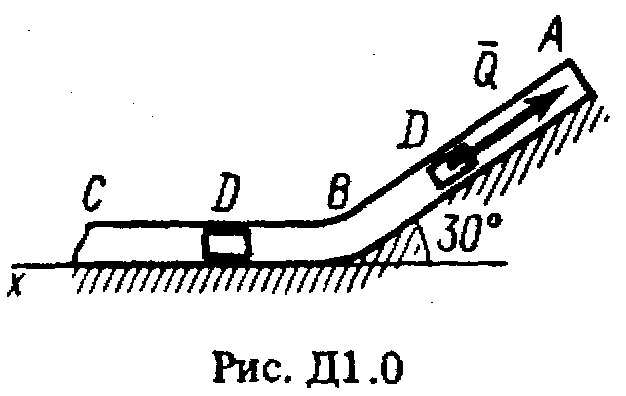
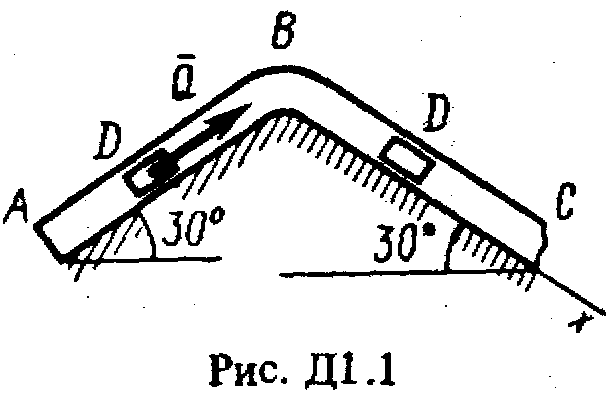
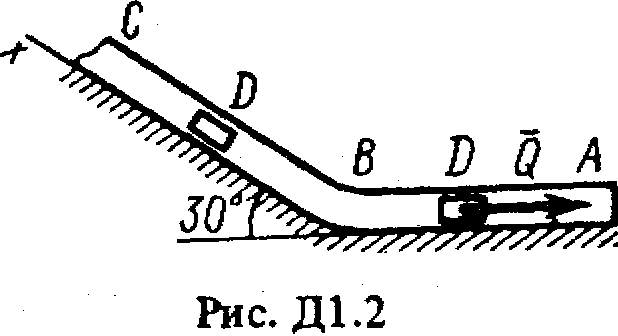
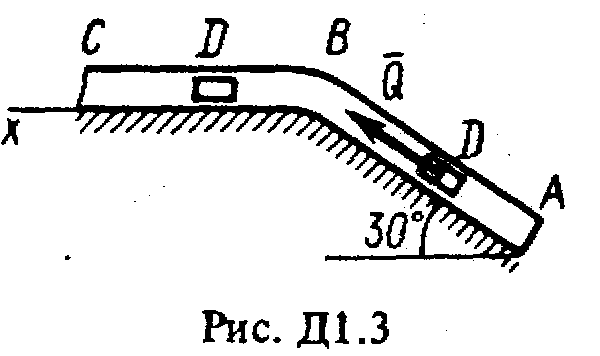
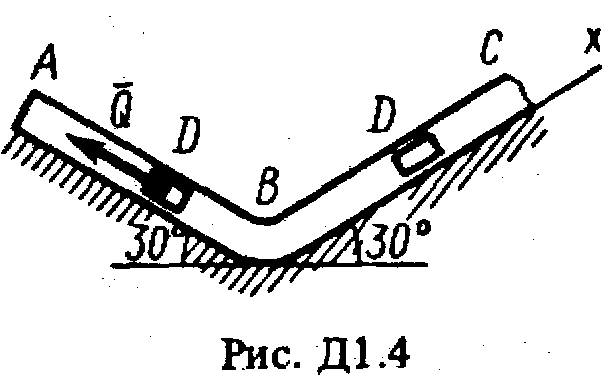
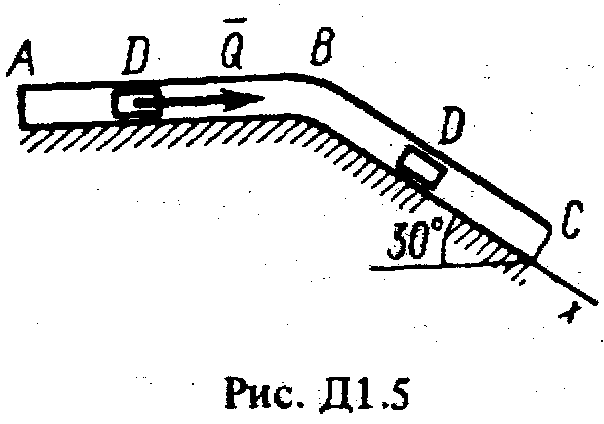
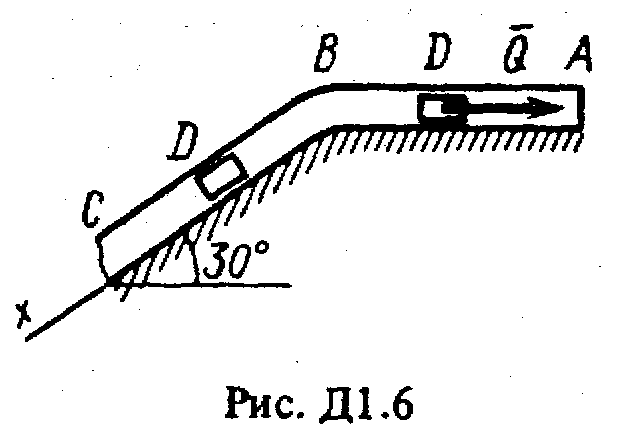
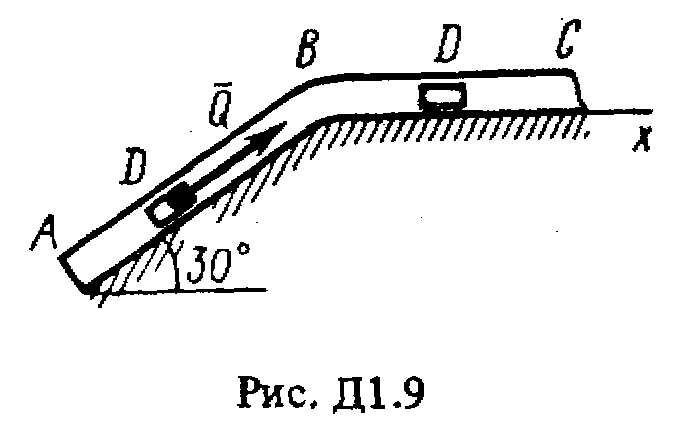
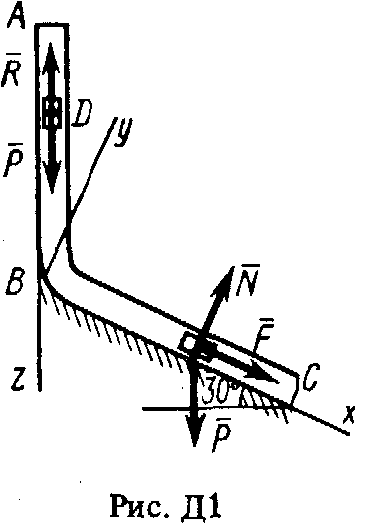
ОСНОВНОЙ

Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа, 2002, 416с.
Никитин Н.Н. Курс теоретической механики. – М.: Высшая школа, 1990, 607с.
Яблонский А.А., Никифорова В.М. Курс теоретической механики. – СПб.: Лань, 2002, 764с.
Мещерский И.В. Задачи по теоретической механике. – СПб.: Лань, 2002, 448с.
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. – СПб.: Лань, 1995, 669 c.

ДОПОЛНИТЕЛЬНЫЙ

Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. – СПб.:Лань, 2002, 729с.
Старжинский В.М. Теоретическая механика. – М.: Наука, 1980, 464с.
Яблонский А.А., Норейко С.С. Курс теории колебаний. – М.: Высшая школа, 1975, 248с.
Бутенин Н.В., Фуфаев Н.А. Введение в аналитическую механику. – М.: Наука, 1991, 255с.
Веселовский И.Н. Очерки по истории теоретической механики. – М.: Высшая школа, 1974, 287с.

ДИНАМИКА
Динамика изучает движение материальных точек и механических систем с учетом сил, которые влияют на это движение.

Задача Д1 (тема: “Динамика точки”)

Груз D массой т, получив в точке А начальную скорость ₀, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0-Д1.9, табл. Д1). На участке АВ на груз кроме силы тяжести действуют постоянная сила

(ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости

груза (направлена против движения).

Таблица Д1

Номер условия	m, кг	₀, м/с	Q, H	R, H	l, м	t₁, с	F_x,H
0	2,4	12	5	0,8²	1,5	-	4sin(4t)
1	2	20	6	0,4	-	2,5	-5 cos(4t)
2	8	10	16	0,5²	4	-	6t²
3	1,8	24	5	0,3	-	2	-2 cos(2t)
4	6	15	12	0,6²	5	-	-5sin(2t)
5	4,5	22	9	0,5	-	3	3t
6	4	12	10	0,8²	2,5	-	6 cos(4t)
7	1,6	18	4	0,4	-	2	-3sin(4t)
8	4,8	10	10	0,2²	4	-	4 cos(2t)
9	3	22	9	0,5	-	3	4sin(2t)

В точке В груз, не изменяя значения своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действует переменная сила

, проекция которой F_x на ось х задана в таблице.

Считая груз материальной точкой и зная расстояние АВ = l или время t₁ движения груза от точки А до точки В, найти закон движения груза на участке ВС, т.е. x=f(t), где х = BD. Трением груза о трубу пренебречь.

Указания. Задача Д1 - на интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке АВ, учтя начальные условия. Затем, зная время движения на участке АВ или его длину, определить, какую скорость будет иметь груз в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая, что в этот момент времени t = 0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти в уравнении к переменному х, учтя, что

Перед выполнением задания прочтите по учебнику тему: «Динамика материальной точки».

Динамика точки (краткие сведения из теории)
Второй закон динамики точки в инерциальной системе отсчета:

, (1)

где m – масса точки,

– абсолютное ускорение точки,

– векторная сумма сил, действующих на точку (равнодействующая). Уравнение (1) – это дифференциальное уравнение движения точки в векторной форме. Спроектировав (1) на оси декартовой системы координат, получаем систему дифференциальных уравнений движения точки в координатной форме:

, (2)

где

и т.д.

Первая задача динамики точки: заданы уравнения движения точки в координатной форме (см. задачу К1)

; (3)

найти силу

, действующую на точку. Решение: получив дифференциальные уравнения (2), дифференцируем заданные функции (3), подставляем в (2), находим

.

Вторая задача динамики точки (основная): задана сила

, действующая на точку; найти кинематические уравнения движения (3) точки. Решение: составив уравнение (1) и спроектировав его на оси, получим уравнения (2). Добавив начальные условия (при

)

проинтегрируем (2) и найдем (3).

Пример Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой т действуют сила тяжести и сила сопротивления

; расстояние от точки А, где  = ₀, до точки В равно l. На наклонном участке ВС на груз действуют сила тяжести и переменная сила F = F (t), заданная в ньютонах.

Дано: т = 2 кг, R = ²,

где  = 0,4 кг/м, ₀ = 5 м/с,

l = 2,5 м, f_х= 16 sin (4t).
Определить: х = f (t) - закон движения груза на участке ВС.

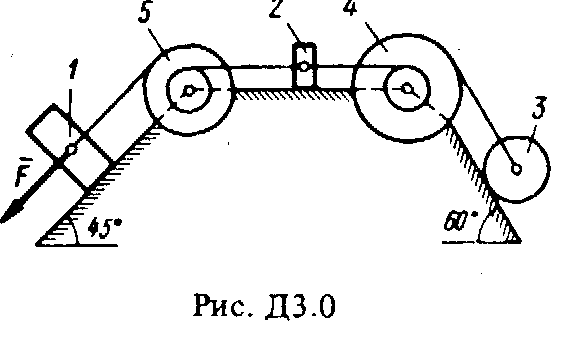
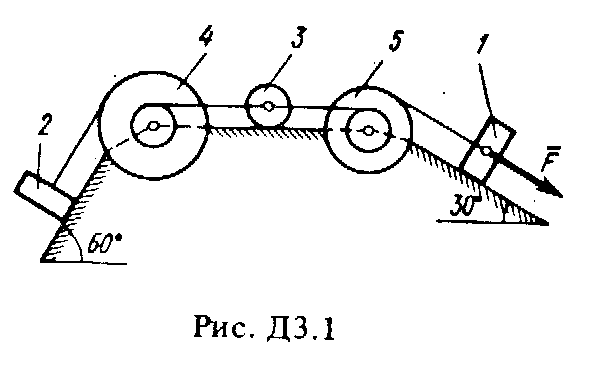
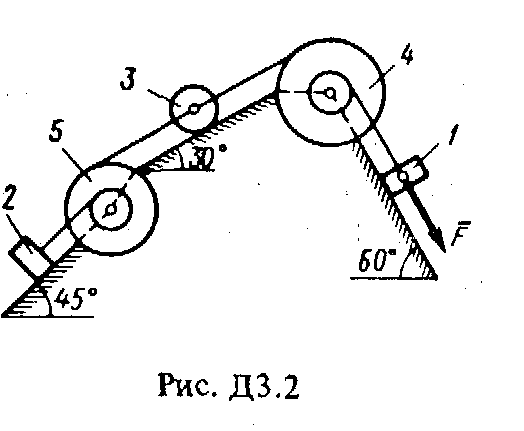
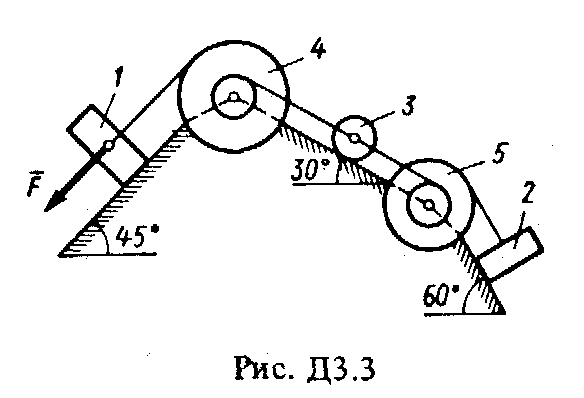
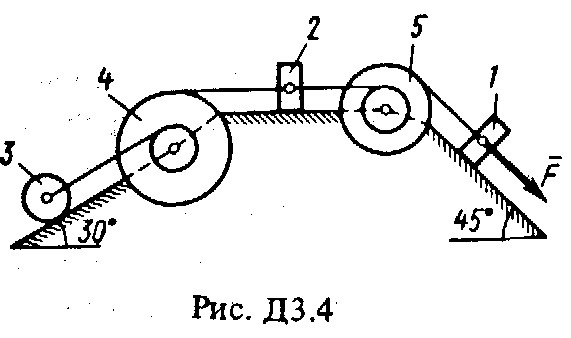
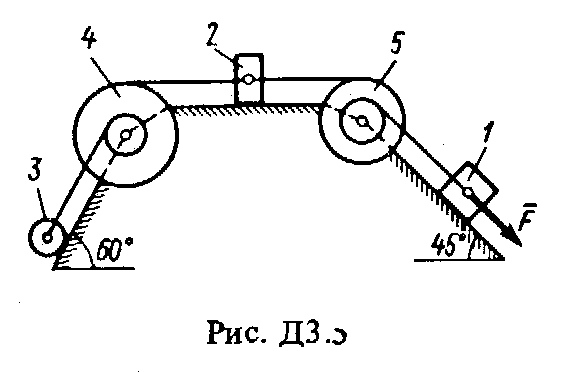
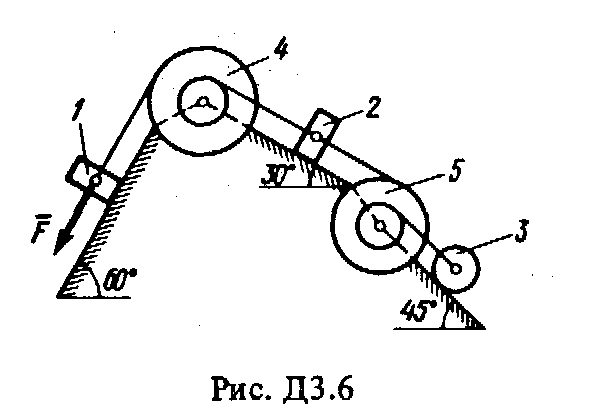
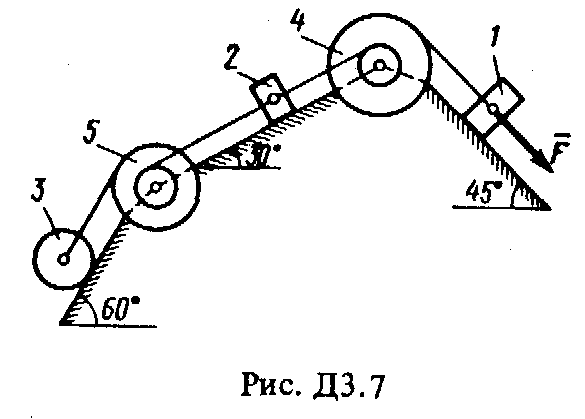
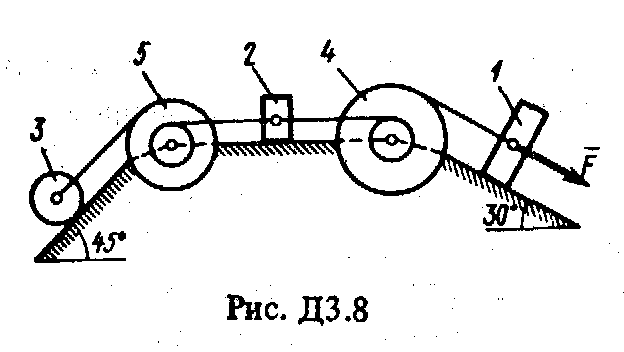
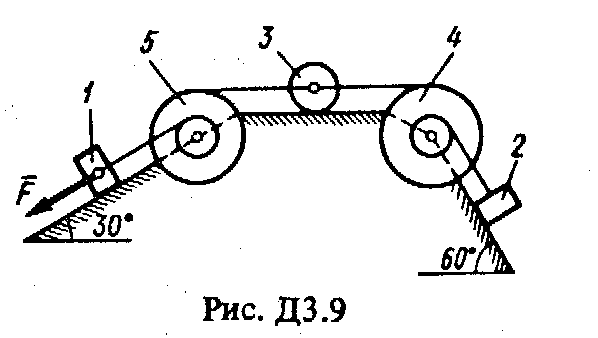
Решение. 1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы

Проводим ось Az и составляем дифференциальное уравнение движения груза в проекции на эту ось:

(1)

Далее находим: Р_z = Р = mg, R_z = -R = -²; подчеркиваем, Что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что _z = , получим

(2)

Введем для сокращения записей обозначения

(3)

где при подсчете принято g  10 м/с². Тогда уравнение (2) можно представить в виде

(4)

Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим

(5)

По начальным условиям при z = 0  = ₀, что дает С₁ =

, и из равенства (5) находим

(6)

Полагая в равенстве (6) z = l= 2,5 м и заменяя k и п их значениями (3), определим скорость _B груза в точке В (₀ = 5 м/с, число е = 2,7) :

(7)

2. Теперь рассмотрим движение груза на участке ВС; найденная скорость _B будет для движения на этом участке начальной скоростью (₀ = _B). Изображаем груз (в произвольном положении) и действующие на него силы

Проведем из точки В ось Вх и составим дифференциальное уравнение движения груза в проекции на эту ось:

(8)

Так как Р_х = Р sin 30° = 0,5 mg, N_x= 0, F_x = 16 sin (4t), то уравнение (8) примет вид

(9)

Разделив обе части равенства на т = 2 кг и полагая опять g  10 м/с², получим

(10)

Умножая обе части уравнения (10) на dt и интегрируя, найдем

(11)

Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t = 0. Тогда при t = 0

, где _B дается равенством (7). Подставляя эти величины в (11), получим

C₂ = _B + 2 cos 0 = 6,4 + 2 = 8,4.

При найденном значении C₂ , уравнение (11) дает

(12)

Умножая здесь обе части на dt и снова интегрируя, найдем

(13)

Так как при t = 0 х = 0, то С₃ = 0, и искомый закон движения груза будет

х = 2,5t² + 8,4t - 0,5 sin (4t), (14)

где х - в метрах, t - в секундах.
Задача Д3

(тема: “Теорема об изменении кинетической энергии системы”)
Механическая система состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R₄ = 0,3 м, r₄ = 0,1 м, R₅ = 0,2 м, r₅ = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу) (рис. Д3.0 – Д3.9, табл. Д3). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям.

Под действием силы F = f (s), зависящей от перемещения точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивлений, равные соответственно M₄ и М₅.

Определить значение искомой величины в тот момент времени, когда перемещение точки приложения силы