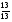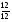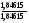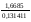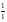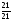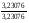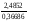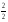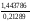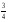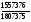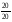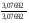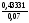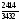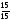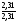Методологические основы моделирования
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
4.Однородные графы. Мера неоднородности. Граф G называется однородным k-связным, если, его вершинная связность æ(G) = k и все степени вершин di = k. Такие графы обладают наибольшей связностью, а следовательно и живучестью при прочих равных условиях. В практике связи встречается большое разнообразие структур, которые выделяются по типам, например, древовидные, радиально-узловые, кольцевые, сотовые, решетчатые, алмазные, k-связные, полносвязные и т.д. Каждая из этих структур имеет свои достоинства и недостатки и в большей или меньшей степени приспособлена для выполнения возложенных функций. Вместе с тем сети связи должны быть приспособлены действовать в условиях активного деструктивного воздействия и обладать наибольшей устойчивостью (живучестью), которая в значительной степени зависит от характеристик связности графа, отображающего эту сеть. Поскольку свойства связности для сетей связи является определяющим то представляет интерес, в какой мере связность у различных структур при заданных m и n отличается от оптимальной, получаемой по рассмотренным алгоритмам, реализующим максимальную однородность графов. Для определения степени неоднородности графа введем меру, аналогичную дисперсии при рассмотрении случайных величин: 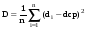 (1) (1)Где: 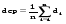 . .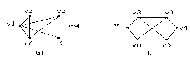 Рис.5. Пример неоднородного (G1 ) и однородного(G2) 3-х-связного графов. Например, для графовG1 и G2 на рис.2.5 с m=9 и n=6 у графа G1dcp = 3; D = 1,67; связность λ=1; для графа у графа G2di = dcp = 3; D = 0; λ=3. Для типовых и преобразованных по алгоритму синтеза оптимальных структур сравнительные данные приведены в таблице. В числителе для типовых, в знаменателе – для преобразованных с таким же числом вершин n и ребер m. Таблица 1.
В таблице в качестве показателей связности использовались: реберная связность λ(G), количество независимых остовных деревьев Тн, количество остовных деревьев Т. Количество независимых остовных деревьев определяется как Тн=m/(n-1) и изменяется от 1 до n/2, количество остовных деревьев изменяется от 1 до достаточно широких пределов и определяется по известной методике, реберная связность изменяется в пределах от 1 до n-1 для полносвязного графа. Как видно из таблицы, при переходе от типовых структур к структурам, синтезированным по оптимальным алгоритмам такие показатели, как количество независимых остовных деревьев и реберная связность не изменяются, за исключением λ(G) для алмазной структуры. Изменяются два показателя- количество остовных деревьев и мера неоднородности, т.е. только они являются чувствительными к изменению структуры, однако вычисление количества остовных деревьев является достаточно громоздкой процедурой, а вычисление дисперсии- простой. При этом увеличение числа остовных деревьев соответствует уменьшению дисперсии. В связи с отмеченными свойствами показателей возникает вопрос об условиях применения того или иного показателя. Кроме того, поскольку желательно получить общие рекомендации для произвольных структур, то необходимо, чтобы число вершин и ребер у всех графов было одинаковым, а менялась только степень неоднородности. Это позволяет глубоко исследовать зависимость связности сетей от степени их неоднородности. Задача генерирования графов с различной степенью неоднородности заключается в разбиении числа 2m на суммы из n членов, каждый из которых равен степени i-ой вершины di(i=1,2…n) при этом dimax ≤n-1, поскольку граф простой, а dimin ≥1, поскольку граф связен. Как отмечалось ранее последовательность П={d1, d2, ..,dn } во- первых должна быть графической, во- вторых упорядочена так, чтобы n-1≥d1≥d2…..≥dn≥1 (1) Возьмем в качестве примера граф, у которого число вершин n=12, число ребер m=36. Наибольшим разнообразием обладает множество, в котором наибольшее число членов отличаются друг от друга. В нашем примере n членов могут принимать значение от 1 до n-1, стало быть два члена одинаковы и находятся в средине вариационного ряда (1) Наименьшим разнообразием обладает последовательность, у которой все степени равны друг другу: diср=dcр=2m/n=const (2) Уменьшение разнообразия неоднородности производится так, чтобы уменьшалось отличие степеней от среднего значения. Наибольшим отличием обладают крайние члены вариационного ряда (1). Поэтому суть алгоритма заключается в добавлении единицы к минимальной степени и вычитание единицы из максимальной до тех пор, пока не будет достигнуто равенство dimin= dimax= dcр. Перечень последовательностей Пi для n=12 и m=36 приведен в таблице. Каждая из последовательностей проверяется на графичность, после чего по этой последовательности строится граф по одному из приведенных ранее алгоритмов ℓ-процедуры. Таблица 2.
Пошаговое выполнение ℓ-процедуры с максимальным ведущим элементам для последовательности П(1)= 11, 10, 9, 8, 7, 6, 6, 5, 4, 3, 2, 1 приведено в таблице 2, а примеры построения по такой же процедуре графов для последовательностей Пi для i=1,7,8 и 16 приведены на рис.6. i=1 i=16 i=7 i=8 Рис.6. Графы последовательностей Пi i=1,7,8 и 16 Поскольку при построении графов на каждом шаге возможны варианты в выборе последующих вершин, то в таблице приведено общее теоретическое число вариантов возможных перестановок вершин с заданными степенями и реальное число вариантов с учетом особенностей алгоритма построения и ограничений на графичность последовательностей. Для каждой из конкретных реализаций графы по последовательностям Пii=1,16 вычислены такие показатели связности как число остовных деревьев и мера неоднородности. Следует заметить, что все рассматриваемые до сих пор графы являются детерминированными, точно также как и показатели: - число остовных деревьев и мера неоднородности также использовались для детерминированных графов. Применение меры неоднородности для случайных графов не вызывает затруднений- более того эта мера, как указывалось ранее, является аналогом дисперсии при описании случайных величин. Подсчет числа остовных деревьев возможен только для конкретных реализаций и эту меру можно обобщать на случай стохастических графов путем усреднения по реализациям. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||