Методологические основы моделирования

• Название: Методологические основы моделирования
• Анкор: sobrannye_lektsii_1_2.docx
• Дата: 07.03.2018
• Размер: 2.94 Mb.
• Имя файла: sobrannye_lektsii_1_2.docx
• Тип: Лекция; #16341
• страница: 17 из 19

Лекция 18.

МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТНО-ВРЕМЕННЫХ ХАРАКТЕРИСТИК СТОХАСТИЧЕСКОЙ СЕТИ.
Прежде чем перейти к рассмотрению способов определения вероятностно-временных характеристик представленного стохастической сетью случайного процесса, докажем существенное свойство эквивалентной функции.

Теорема 1

Стохастическая сеть, соответствующая стационарному случайному процессу имеет эквивалентную функцию, голоморфную при Re s >0.

Доказательство.

Рассмотрим стохастическую сеть произвольной структуры (рис.11).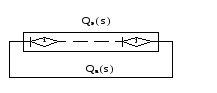



Рис. 11

На рис.11 Q_э(s) - эквивалентная функция стохастической сети; Q_a(s)=1/Q_э(s) - дополнительная дуга, соединяющая сток j c источником i.

Функция Q_э(s) определяется из топологического уравнения Мейсона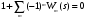

, (21)

где W_m(s) - эквивалентные функции петель m-го порядка, определяемые как произведение эквивалентных функций w_i(s)m не связанных между собой петель первого порядка, то есть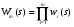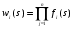

;

; -

- эквивалентная функция i-й петли первого порядка;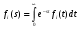

,

- преобразование Лапласа функции плотности распределения вероятностей времени свершенияi-го элементарного процесса. Исходя из свойств преобразований Лапласа, функция f_i(s) является голоморфной.

С учетом (21), эквивалентная функция Q_э(s) для сети произвольной структуры имеет вид: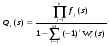

, (22)

где k – количество функций f_i(s) в прямой цепи стохастической сети; M – максимальный порядок петель данной стохастической сети.

Несложно видеть, что производная функции (22)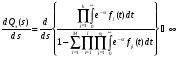

,

существует в окрестности каждого полюса s₀ и не изменяет своего знака в области определения, а значит Q_э(s) является голоморфной. Теорема доказана.

Доказанное свойство голоморфности эквивалентной функции обусловливает правомочность следующих двух основных подходов к определению вероятностно-временных характеристик представленного стохастической сетью случайного процесса.

1.Метод двухмоментной аппроксимации.

Особенностями этого метода является:

1. 
   Придание вероятностного смысла эквивалентной функции стохастической сети: Q(s) – вероятность того, что процесс передачи сообщений по системе связи будет завершен успешно до случайного момента времени старения этих сообщений.
   
2. 
   Принятие ограничений на вид функции распределения времени старения передаваемой информацииZ(t).
   

В общем случае, вероятность того, что случайное время передачи t_П, распределенное по закону H(t), будет меньше случайного времени старения информации t_c, распределенное по закону Z(t) равна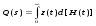

. (23)

При использовании преобразования Лапласа - Стилтьеса

Z(t)= 1 – exp[-t/ t_c],

а параметр преобразования s = 1/t_cимеет смысл интенсивности старения передаваемой информации. Отсюда, вероятность своевременной передачи сообщений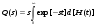



и является, по существу, характеристической функцией, позволяющей определить k-е начальные моменты случайного времени реализации стохастической сети по формуле: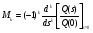

. (24)

Отсюда среднее время передачи сообщения, определяемое как начальный момент первого порядка равно: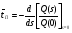



а дисперсия времени передачи D[t_П], определяемая как второй центральный момент, вычисляется по формуле: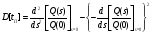

.

Вычисление математического ожидания t_Пи дисперсии D[t_П] позволяет приближенно определить функцию распределения времени передачи как неполную гамма – функцию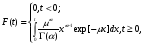

(25)

где 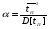, 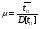- параметры формы и масштаба, соответственно.

Таким образом, реальная функция распределения времени передачи была аппроксимирована неполной гамма - функцией, с параметрами, определяемыми из эквивалентной функции стохастической сети, что и дало название этому методу. Следует заметить, что если исследователю априорно известен закон распределения, наиболее полно характеризующий исследуемый процесс, то аналогичным образом можно выполнить аппроксимацию этим законом реальной функции распределения.

Описанный метод позволяет получать достаточно точные результаты при моделировании систем массового обслуживания и обуславливает его широкое использование специалистами для моделирования систем связи общего назначения. Однако при моделировании систем связи ВМФ, из-за несоответствия закона старения передаваемой информации реальному, применение метода двухмоментной аппроксимации может привести к существенным ошибкам. Поэтому для получения более точных результатов моделирования и при решении исследовательских задач необходимо использовать второй подход.

2.Метод обращения.

В отличие от первого, второй подход к определению вероятностно-временных характеристик систем связи не предусматривает ограничений на вид закона распределения времени старения передаваемой информации. Поэтому, эквивалентная функция стохастической сети рассматривается не как вероятность своевременной передачи, а как изображение исследуемого процесса доставки сообщений по Лапласу. Действительно, функция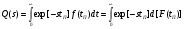

, (26)

является классическим представлением интегрального преобразования Лапласа функции–оригинала f(t_П) - функции плотности вероятностей времени t_П. В свою очередь, определение изображений подпроцессов исследуемого процесса передачи и сам алгоритм формирования эквивалентной функции является типичным для операционного исчисления методом, широко применяемым для исследования сложных функций. Что касается параметра s, то в данном случае он представляет собой не интенсивность старения передаваемой информации, а является комплексной переменной:

s =  + jy, - < y < +.

Таким образом, интеграл (26) является преобразованием Лапласа, ставящим в соответствие каждой функции (оригиналу) f(t_П), t_П> 0, единственную функцию Q(s) (изображение) комплексной переменной, причем для существования изображений необходима сходимость этого интеграла. Отсюда вытекает первый важный шаг анализа – проверка сходимости интеграла Лапласа. Напомним, что признаком абсолютной и равномерной сходимости (26) является существование предела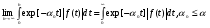



и аналитичность функции Q(s), приRe(s) = ₀ Точная нижняя грань _a действительных чисел ₀,для которых выполняется это условие называется абсциссой абсолютной сходимости преобразования Лапласа. При этом в полуплоскости Re(s)₀ изображение Q(s), определяемое из стохастической сети с использованием уравнения Мейсона, как было доказано выше, является голоморфной (однозначной аналитической) функцией. Областью определения функции Q(s) является полнаяs-плоскость, за исключением особых точек, расположенных слева от прямой =_a.

После проверки сходимости интеграла Лапласа, следует второй шаг, состоящий в переходе из пространства изображений в пространство оригиналов, т.е. осуществление обратного преобразования Лапласа, основанного на теореме обращения (см. Преобразования Лапласа).

Достаточными условиями существования обратного преобразования являются:

• 
  Если Q(s) аналитична для _a и имеет порядок меньше –1, то обратное преобразование Лапласа L^-1[Q(s)] существует; оно непрерывно для всех t>0 и f(t) асимптотически сходится к функции exp[_at] при t с абсцисой абсолютной сходимости _a, а при t  0 L^-1[Q(s)]  0;
  
• 
  Если Q(s)=[Q_i(s), i=1,n], при (s_i, i=1,n)аналитичной относительно каждого s_i, равна нулю при s_i=0, i=1,n и Q_i(s) = L[f_i(t)] (_ai,i=1,n), то L^-1[Q(s)] существует и соответствующее преобразование Лапласа имеет абсциссу абсолютной сходимости.
  

Задача определения оригинала f(t), соответствующего эквивалентной функции стохастической сети Q(s) является достаточно сложной и для ее решения используются способ контурного интегрирования и методы разложения Q(s) (с целью упрощения ее вида), с последующим почленным переходом в пространство оригиналов.

Способ контурного интегрирования подразумевает полное определение функции Q(s) для всех значений комплексной переменной s=α+jy, -, а поэтому его использование зачастую весьма трудоемко и на практике применяется достаточно редко.

Значительно упростить процедуру обращения (перехода от Q(s) к f(t)) позволяют методы разложения, причем в зависимости от вида эквивалентной функции используются различные разложения. Рассмотрим их более подробно.

1. 
   Эквивалентная функция Q(s) является рациональной алгебраической функцией.
   

Разложение Хевисайда.

В этом, самом распространенном случае, эквивалентная функция представляется в виде отношения двух многочленов f(s) иφ(s), степеней m и n соответственно, т.е.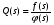

, deg[f(s)]=m; deg[φ(s)]=n; n>m

где deg[*] – степень соответствующего многочлена.

Условие n>m позволяет использовать теорему о вычетах и при

φ(s) = a₀(s - s₁)(s - s₂)…(s – s_i)…(s - s_n), s_i s_i+1 , i = 1,n;

представить эквивалентную функцию в виде суммы: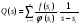

,

где φ’(si) –значение производной многочлена знаменателя в точке s_i. А значит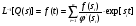

.

В случае кратных корней, т.е. если

φ(s) = a₀(s - s₁)^a₁ (s - s₂)^a₂ …(s – s_i)^a_i … (s - s_n)^a_n , s_i s_i+1 , i = 1,n;

оригинал определяется по формуле: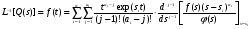

.

Если φ(s) имеет комплексно сопряженные корни s = αjy, то пары членов, соответствующих этим корням можно преобразовать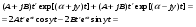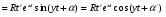



,

гдеR = 2A²+B²; = -arctg[A/B]; ^ = arctg[B/A]. При этом, если A, B, R, и^ - являются действительными, то и L^-1[Q(s)] = f(t) является действительной функцией.

3.Разложение на простые дроби.

В этом случае эквивалентная функция Q(s) = f(s)/φ(s) представляется в виде суммы n элементарных дробей (n = deg[f(s)]), соответствующих корням s_iкратности a_iмногочлена φ(s):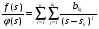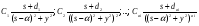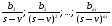

.


.

где C_ai, d_ai– коэффициенты, определяемые в соответствии с пунктом 1).

Если корни s_iявляются комплексными, то каждой паре комплексно-сопряженных корней s = φjyсоответствует a_i простых дробей

Коэффициенты b_kj определяются путем:

При этом, если f(s) и φ (s) не имеют совпадающих корней, то каждому действительному корню s_i = v уравнения φ (s)=0 соответствует a_iпростых дробей

1. 
   умножением обеих частей на φ (s) и последовательным дифференцированием полученных равенств.
   
2. 
   умножением обеих частей последнего равенства на φ (s) и приравниванием коэффициентов при одинаковых степенях s в обеих частях полученного равенства;
   

Эквивалентная функция представляет собой сложную или неявнозначную функцию

В этом, достаточно редко встречающемся случае, эквивалентную функцию раскладывают в сходящийся ряд, для каждого члена которого определяется обратное преобразование Лапласа, а оригинал (искомая функция плотности) определяется как сумма полученных частных оригиналов. Метод разложения в ряды опирается на следующую теорему.

Теорема.

Пусть Q(s) можно представить в полуплоскости Re(s)  в виде ряда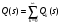

,

гдеQ_k(s) =L[f_k(s)] (_a, k=1,2,…). Пусть далее все интегралы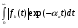



существуют и сходится ряд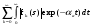

.

Тогда ряд 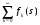сходится абсолютно к функции f(t) почти для всех t и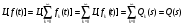

, при α>α_а.

Наиболее часто получается разложение эквивалентной функции Q(s) в ряд по отрицательным степеням s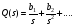

.

Если этот ряд сходится при |s| > 0, то при t > 0 искомая плотность вероятностей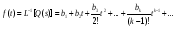

.

Заметим, что иногда для представления Q(s) в виде сходящегося ряда приходится использовать разложение Лорана.

В том случае, когда применение описанных методов разложения затруднительно целесообразно использовать разложение в асимптотические ряды [5].

А) Асимптотическое разложение изображения.

Пусть Q(s) = L[f(t)] и оригинал f(t) может быть разложен в окрестности точки t= 0 в абсолютно сходящийся ряд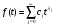

,____j

Тогда Q(s) имеет при s асимптотическое разложение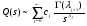

.

Б) Асимптотическое разложение оригинала.

Если Q(s) = L[f(t)], (>_a) и выполняются следующие условия:

1. 
   Q(s) имеет лишь изолированные особые точки – полюсы и алгебраические точки разветвления;
   
2. 
   Q(s) в полуплоскости Re(s) < 0 стремится к нулю при |s| ;
   
3. 
   Число особых точек s =s_k с наибольшей действительной частью конечно (k = 1,l) и разложение Q(s) в окрестности каждой такой точки задается рядом
   

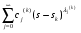,N_k^_^_^_j 

то оригинал f(t) имеет при t  асимптотическое разложение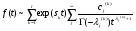

.

После определения функции плотности распределения вероятностей времени передачиf(t)=L^-1 [Q(s)] одним из описанных выше методов можно определить:

функцию распределения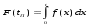

(27)

среднее время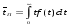

(28)

и дисперсию времени передачи сообщений по системе связи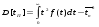

. (29)

Таким образом, мы ознакомились с двумя наиболее известными подходами к определению вероятностно – временных характеристик процесса функционирования систем связи. Следует отметить, что применение того, или иного подхода определяется целью исследования и требованиями к точности определения характеристик этого процесса. Как показал опыт, наиболее распространенным является первый подход, однако из-за известных ограничений более предпочтительным является второй. При его использовании следует учитывать, что эквивалентная функция стохастической сети, как правило, представима в дробно – рациональном виде с действительными корнями многочлена знаменателя. Это определяет преимущественное использование разложения Хевисайда для упрощения эквивалентной функции и определения оригинала при решении практических задач по оценке эффективности функционирования систем связи

Так как целью исследования реальных систем является определение не только вероятности и времени передачи информации по системе связи, но и ее устойчивости, то представляется достаточно интересным определение основных характеристик процесса функционирования системы связи и ее элементов.