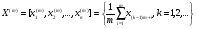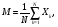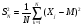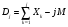Методологические основы моделирования
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
Лекция 15 Введение во фракталы Английские военные топографы еще до войны заметили, что длина побережья Великобритании зависит от длины линейки, которой ее измеряют. Аналогичная зависимость определяет длину некоторых рек, побережье многих островов, путь, проходимый частицей при броуновском движении, и многое другое. В качестве наглядного примера можно привести так называемый «остров Коха». На рис. 5.5 показано, как можно построить такую фигуру. 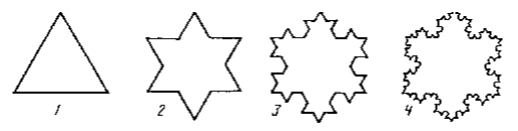 Рис. 5.5. Схема построения острова Коха На первом шаге берем обычный равносторонний треугольник (рис. 5.5). Потом на каждой стороне достраиваем по треугольнику, сторона которого в три, а значит, площадь в девять раз меньше, чем у исходного треугольника и так далее. То, что получится после бесконечного количества таких шагов, называется островом Коха. При этом длина его побережья бесконечна, поскольку на втором шаге периметр фигуры увеличится в 4/3 раза, на третьем - еще в 4/3 и т. д. Это происходит потому, что каждый отрезок мы заменили ломаной, длина которой в 4/3 раза больше. Таким образом, периметр данной фигуры p 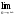 4/3n . При этом с помощью формул геометрической прогрессии можно убедиться, что площадь острова Коха конечна. 4/3n . При этом с помощью формул геометрической прогрессии можно убедиться, что площадь острова Коха конечна. Теперь представим себе, что мы решили измерить периметр острова Коха, пользуясь линейкой определенной длины. При этом мы, конечно, будем заменять сложную изрезанную береговую линию ломаной со звеньями, не меньшими, чем наша линейка, как это всегда делают географы. Измеренный периметр будет зависеть от длины линейки. Это кажется совершенно неожиданным. Но действительно, чем меньше длина линейки, тем больше измеренная длина побережья. Остров Коха обладает еще одной интересной особенностью. Допустим, что мы фотографируем этот остров в океане из космоса. Мы можем фотографировать с любым увеличением, но часть побережья будет тем меньше, чем больше увеличение и мелкие детали в крупном масштабе, естественно, будут теряться. Типичная картина, которую мы увидим, показана на рис. 5.6. В крупном масштабе видим большой зубец и несколько маленьких. Увеличим маленький зубчик. То есть, по существу, увеличим маленький прямоугольник до размеров первоначального. Опять выделим маленький прямоугольник, опять увеличим и опять увидим то же самое и так до бесконечности. Это свойство, выглядеть в любом, сколь угодно мелком масштабе примерно одинаково, называется масштабной инвариантностью, а множества, которые им обладают - фракталами. Можно спросить, как же характеризовать фракталы, если размеры становятся какими-то зыбкими, ненадежными и начинают зависеть от размеров линейки? 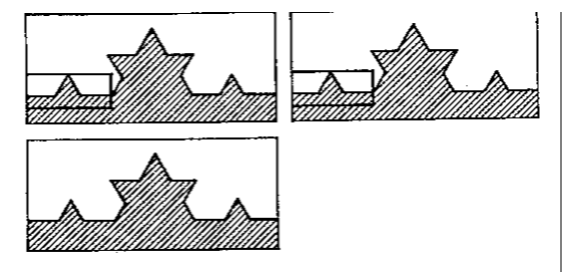 Рис. 5.6. Пример фрактальной масштабной инвариантности На это математики могут ответить просто и остроумно: «Важна не сама длина, а то, как она зависит от размеров линейки, т. е. важно некое число, называемое фрактальной размерностью». Для отрезка размерность равна 1, для квадрата - 2, для куба - 3. Для фракталов размерность - дробное число. Отсюда и само название «фрактал», происходящее от английского «fractal» - дробный, неполный, частичный. Например, для острова Коха оно лежит между 1 и 2 - полоса в двумерном пространстве, т. е. уже не обычная кривая, но еще не плоскость (дробная размерность). 5.2.2. Самоподобные (фрактальные) случайные процессы Представленный пример фрактала (кривая Коха) относится к классу детерминированных фракталов, т. е. когда объект непосредственно составляется из своих малых копий. В теории телетрафика для описания поведения величины нагрузки в сетях связи с пакетной коммутацией применяется класс случайных (стохастических) фракталов. В этом случае свойство самоподобия (масштабной инвариантности) наблюдается лишь «в среднем», т. е. подобными являются не сами отсчеты сигнала, а, например, его КФ или ПРВ в разных временных масштабах. Три характерные особенности самоподобных процессов выражены в медленном убывании дисперсии, долгосрочной зависимости и флуктуационном характере спектра мощности таких процессов. Рассмотрим дискретную случайную последовательность отсчетов: Xxi,i=1,2,...}, где xi- СВ с заданным законом распределения. Будем предполагать, что все рассматриваемые СП имеют ограниченную ковариацию B(xi,xi),и следовательно дисперсию xiB(xi,xi).СП будет обладать свойством самоподобия, если агрегированный процесс m-го порядка
будет иметь КФ r(m)(k)совпадающую с КФ r(k)исходного СП для любых m. При выполнении данного условия можно утверждать, что дисперсия агрегированного процесса X(m)убывает согласно выражению
т. е. дисперсия агрегированных процессов – средних выборок – уменьшается медленнее, чем величина, обратная размеру выборки. В результате в самоподобных процессах имеет место явление долгосрочной зависимости, которое приводит к расходимости КФ процесса:
Наконец энергетический спектр самоподобных процессов описывается выражением
Собственно эти соотношения и определяют название самоподобного процесса: корреляционные свойства такого процесса, усредненного на различных временных интервалах, остаются неизменными. Важнейшим параметром, характеризующим «степень» самоподобия СП, является параметр Хёрста. Для выборочного случайного набора Xj (j1,...,Nможно определить выборочное среднее
выборочную дисперсию
и интегральное отклонение
Определим изменчивость СП на интервале N как неубывающую функцию длины интервала
Хёрстом было показано, что для большинства естественных процессов при больших значениях N выполняется соотношение 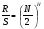 или иначе
Величина H получила название параметра Хёрста и лежит в интервале 0.5 1.0 H << . Для процессов, не обладающих свойством самоподобия, H =0.5. Для самоподобных процессов с долгосрочной зависимостью этот параметр изменяется в пределах 0.7…0.9. Параметр β, который был введен выше для задания асимптотических свойств характеристик самоподобных СП, может быть выражен через параметр Хёрста: 22H. Степень самоподобия процесса можно оценить другим способом: параметр Херста можно определить путем построения графика отношения log(RN/SN) в зависимости от logN/2при разных N и вычислить величину H как тангенс угла наклона полученной линии. Следует заметить, что полученное множество точек не будут лежать на одной линии, поэтому их следует аппроксимировать линией, например, по методу наименьших квадратов. Данная методика определения параметра Херста получила название R/S-метод. R/S-метод дает лишь приближенное значение показателя Херста, поэтому для его вычисления целесообразно пользоваться несколькими методиками и сравнения полученных результатов. Рассмотрим метод определения величины H на основе периодограммного анализа. Для самоподобного СП Xxiвычисляется периодограмма 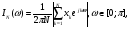 где N - количество отсчетов временного ряда. Учитывая, что самоподобие влияет на характер спектра S(), должен получаться график зависимости спектральной плотности вида IN()12H, при0. Из последнего выражения следует, что множество случайных точек (log[IN];log()) будет располагаться линейно с коэффициентом наклона линии 1-2 H . На практике для вычисления оценки должны использоваться только нижние 10% частот, т. к. описанное выше поведение справедливо только для области частот, близких к нулю. Основным недостатком данного метода является большой объем вычислений при построении оценки показателя Херста. 5.3. Модели систем массового обслуживания Допущения о пуассоновском характере потока заявок и о показательном распределении времени обслуживания позволяют применить в теории массового обслуживания аппарат марковских СП. Процесс, протекающий в физической системе, называется марковским (или процессом без последействия), если для каждого момента времени вероятность любого состояния системы в будущем p(t0∆ t)зависит только от состояния системы в настоящий момент pt0и не зависит от того, каким образом система пришла в это состояние. Рассмотрим СМО с конечным дискретным множеством состояний (рис. 5.9). Определим состояние xkкак состояние СМО, соответствующее наличию в данный момент k занятых каналов. При этом система может изменять свое состояние xkдискретно в соответствующие дискретные моменты времени ti. При поступлении на вход СМО одной заявки система изменяет свое состояние с xkна xk1, а при уходе одной заявки из системы и соответствующем освобождении одного канала - с xkна xk1.  Рис. 5.9. Диаграмма состояний и переходов СМО Типичным примером СМО является телекоммуникационная система с несколькими обслуживающими серверами. Заявка, поступающая на вход такой СМО, может быть либо обслужена, либо поставлена в очередь, либо получить отказ в обслуживании. В связи с этим СМО делятся на два основных типа: а) СМО с отказами; б) СМО с ожиданием. В системах с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, немедленно получает отказ, покидает систему и в дальнейшем процессе обслуживания не участвует. В системах с ожиданием заявка, заставшая все каналы занятыми, не покидает систему, а становится в очередь и ожидает, пока не освободится какой-нибудь канал. Лекция 16. СУЩНОСТЬ И СОДЕРЖАНИЕ МЕТОДА ТПСС Для исследования систем с обратной связью в радиотехнике нашли широкое применение сигнальные и потоковые графы, методы исследования которых были разработаны С.Мэзоном еще в 1953 году. А. Присткер и В. Харп применили теорию потоковых графов к исследованию временных процессов. Так как процесс передачи потоков сообщений по сетям связи является случайным временным процессом, то академиком Захаровым Г.П. был предложен, а его учениками успешно использован для анализа систем связи общего назначения метод топологического преобразования стохастических сетей (ТПСС). Суть метода заключается в том, что исследуется не система, а целевой процесс, который она реализует. Этот сложный процесс декомпозируется на элементарные процессы, каждый из которых характеризуется функцией распределения или средним и дисперсией времени его выполнения. Логика и последовательность выполнения процессов определяется двухполюсной сетью, состоящей из входного, промежуточных и выходного узлов (вершин), при этом ребрам соответствует набор элементарных процессов, а вершинам (узлам) условия их выполнения. Каждый узел выполняет две функции – входную, определяющую условие выполнения узла и выходную, определяющую какие из операций, следующих за узлом, будут выполняться. Входной узел сети выполняет только выходную функцию, а выходной только входную. Для каждого из ребер определяется функция передачи – условная характеристическая функция, являющаяся преобразованием Лапласа функции плотности распределения вероятностей времени свершения элементарного процесса. Далее осуществляется топологическое преобразование стохастической сети по правилу Мэйсона. При этом топологическим инвариантом является свойство связности сети. Поскольку входная и выходная вершины двухполюсной сети (графа) являются связными, то топологическое преобразование приводит к получению эквивалентной функции, сохраняющей в своей структуре параметры распределения и логику взаимодействия элементарных случайных процессов. Получение эквивалентной функции позволяет известными методами определить первые моменты случайного времени выполнения целевого процесса либо произвести ее обратное преобразование по Лапласу (определить ее оригинал в пространстве изображений Лапласа), результатом которого является функция плотности вероятностей времени выполнения этого процесса. Таким образом, сущность метода ТПСС состоит в представлении анализируемого процесса в виде стохастической сети, замене множества элементарных ветвей сети одной эквивалентной и последующим определением эквивалентной функции сети, начальных моментов и функции распределения случайного времени ее реализации, т.е. реализации анализируемого процесса. Из сущности метода ТПСС следует, что для его применения необходимо правильное, не искажающее физического смысла представление анализируемого процесса функционирования системы связи или ее элемента стохастической сетью. Поэтому изучение метода начнем со знакомства с элементами стохастических сетей. 1. Стохастические сети и их элементы Под стохастической сетью пронимается совокупность взаимоувязанных узлов (вершин) и ветвей, соединение которых соответствует алгоритму функционирования исследуемой системы. При этом сеть реализуется, если будет выполнено некоторое подмножество ветвей, время реализации которых выбирается в соответствии с вероятностным распределением. Как следует из определения, стохастическая сеть состоит из вершин (узлов) и ветвей. Вершина стохастической сетихарактеризуется вероятностью его реализации и может быть интерпретирован как состояние системы. Поскольку стохастическая сеть является двухполюсной, то ее вершины подразделяются на входную, выходную и промежуточные (внутренние). Каждая промежуточная вершина сети состоит из входной (приемной) и выходной (распределительной) частей, отображающих те, или иные логические операции. В настоящее время используются 3 вида входных («И», «ИЛИ» и «Иск.ИЛИ») и 2 выходных («детерминированный» и «вероятностный») частей вершин. Графическое представление различных типов вершин показано в табл.1. Таблица1.
Входная часть вершины определяет условие (логическую операцию), при котором она может быть выполнена. Выходная часть определяет совокупность условий, определяющих возможность выполнения данной вершины. Другими словами выходная функция показывает, все ли исходящие из вершины ветви должны быть выполнены, или только одна из них. Рассмотрим указанные типы вершин более подробно. «Исключающее ИЛИ» - предусматривает реализацию вершины при выполнении любой ветви, входящей в данную вершину. При этом, одна и только одна ветвь может быть реализована в заданный момент времени. «Включающее ИЛИ» – реализация любой ветви, входящей в вершину приводит к ее реализации. Временем ее реализации является минимальное время свершения подпроцессов, соответствующих любой из входящих ветвей. «И» – данная вершина будет реализована только тогда, когда все входящие в нее ветви реализуются. Время реализации такой вершины соответствует максимальному времени свершения подпроцессов, соответствующих всем входящим ветвям. «Детерминированный выход» - в случае реализации вершины, используются все исходящие из нее ветви. Все ветви начинающиеся от этой вершины реализуются с вероятностью равной единице. «Вероятностный выход»- при реализации вершины, в лучшем случае используется одна исходящая ветвь. В зависимости от вида входной и выходной частей вершины ей присваивается соответствующее наименование. При этом, на первое место ставится вид выхода, а на второе – вид входа. Например, детерминированная вершины «И», вероятностная вершина «Включающее ИЛИ» и т.д. Очевидно, что с использованием перечисленных видов вершин можно достаточно точно описать алгоритмы и процессы функционирования различных средств связи, процессы принятия решений, обучения и т.п. Следующим элементом стохастической сети является ветвь, интерпретируемая как переход из одного состояния в другое и характеризующаяся:
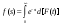 . .Следует заметить, что в качестве второй характеристики ветви может быть использована производящая функция моментов, характеристическая функция или любое другое интегральное преобразование. Выбор и использование в дальнейшем именно преобразования Лапласа обусловлено ясностью физического смысла, а также полнотой разработки математического аппарата этого раздела операционного исчисления. 2. Понятие эквивалентной функции стохастической сети Рассмотрим сеть G = (N,A). Вершины данной сети образуют множество N, а ветви - множество A. Пусть время реализации ветви aij, соединяющей i и j вершины есть случайная величина tij. Понятно, что ветвь aij может быть реализована только в том случае, если будет выполнена вершина i. Следовательно, необходимо знать условную вероятность (в дискретном случае) или плотность распределения (в непрерывном случае) случайной величины tijпри условии, что вершина i выполнена. Положим fij(t) - условная вероятность или плотность распределения времени реализации ветви aij , а преобразование Лапласа, совпадающее с характеристической функцией случайной величины tij определяется как 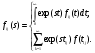 Обозначим pij– вероятность того, что ветвь aij будет реализована при условии выполнении вергшиныi. Тогда: для представленного стохастической сетью случайного процесса эквивалентная функция Qij(s) определяется по формуле Qij(s) = pijfij(s). (15) То есть ф(15) ставит в соответствие исходной стохастической сети Gэквивалентную ей сеть G ‘, которая характеризуется всего одним параметром – эквивалентной функцией Qij(s), (рис.1).  Рис. 1 Рассмотрим 3 базовые структуры стохастических сетей в предположении независимости случайных величин, преобразования Лапласа функций плотности вероятностей которых характеризуют соответствующие ветви сети. При рассмотрении будем полагать, что указанными случайными величинами являются случайные времена реализации ветвей стохастической сети. |