Методологические основы моделирования

• Название: Методологические основы моделирования
• Анкор: sobrannye_lektsii_1_2.docx
• Дата: 07.03.2018
• Размер: 2.94 Mb.
• Имя файла: sobrannye_lektsii_1_2.docx
• Тип: Лекция; #16341
• страница: 16 из 19

Последовательное соединение ветвей стохастической сети.

Рассмотрим фрагмент стохастической сети (рис.2), ветви которой характеризуются эквивалентными функциями Q_ij(s) и Q_jk(s).



Рис. 2

По существу фрагмент соответствует случайному процессу, состоящему из двух последовательно протекающих подпроцессов, каждый из которых реализуется за некоторое случайное время. Пусть времена реализации равны t_ij и t_jk. Тогда, суммарное время реализации будет равно

t_ = t_ij + t_jk.

В свою очередь, преобразование Лапласа функции плотности вероятностей времениt_ равно произведению преобразований соответствующих функций плотности, т.е.

F_ik(s) = f_ij(s)f_jk(s),

а вероятность совместной реализации этих двух подпроцессовp_ik = p_ijp_jk.

ОтсюдаQ_(s) = Q_ik(s) = p_ijf_ij(s)p_jkf_jk(s) = Q_ij(s)Q_jk(s).

То есть, последовательное соединенные ветви сохраняют связность входной и выходной вершин сети. Поэтому последовательное соединение ветвей топологически эквивалентно одной ветви, а «след» от их объединения остается в формуле эквивалентной функции. Это справедливо и для n последовательно соединенных ветвей.

Несложно видеть, что стохастическая сеть, состоящая из n последовательно соединенных ветвей имеет эквивалентную функцию вида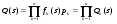

(16)

и значит эквивалентная функция стохастической сети, состоящей из последовательно соединенных ветвей равна произведению эквивалентных функций этих ветвей.

Параллельное соединение ветвей стохастической сети.

Рассмотрим стохастическую сеть (рис.3), состоящую из двух параллельных ветвей, характеризующихся вероятностями их выбора p_aи p_b, а также преобразованиями Лапласа функций плотности f_a(s) и f_b(s) вероятностей времен их реализации.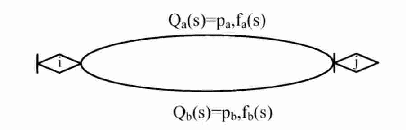



Рис. 3

Определим эквивалентную функцию Q_ij(s) этой стохастической сети.

По определению эквивалентной функции Q_ij(s) = p_ijf_ij(s).

При этом,p_ij = p_a+p_bи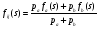

.

Поэтому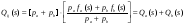

.

Следовательно, если стохастическая сеть состоит из n параллельно соединенных ветвей, то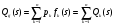

. (17)

Таким образом, эквивалентная функция стохастической сети, состоящей из параллельно соединенных ветвей равна сумме эквивалентных функций этих ветвей.

Петли.

Связная замкнутая последовательность ориентированных ветвей стохастической сети, каждая вершина которых является общей ровно для двух ветвей или ветви, соединяющие вершину саму с собой, называется петлей.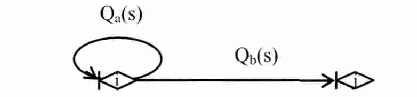



Рис. 4

Рассмотрим стохастическую сеть (рис.4), состоящую из ветвей a и b. Реализация ветви a приводит к повторной реализации i-го узла, а реализация второй – к реализации j-го исходящего узла сети.

Ветви характеризуются соответствующими эквивалентными функциями Q_a(s) и Q_b(s). Определим эквивалентную функцию стохастической сети указанного вида.

Для определения эквивалентной функции представим исходную сеть в виде бесконечной последовательности параллельных цепей, каждая из которых состоит из последовательно соединенных ветвей (рис.5).

В этом случае эквивалентными функциями цепей сети (рис.5) являются: Q_b(s), Q_b(s)Q_a(s), Q_b(s) Q_a²(s), Q_b(s) Q_a³(s),…, Q_b(s) Q_aⁿ(s),... Отсюда, эквивалентная функция стохастической сети равна

Q_ij (s) = Q_b(s) + Q_b(s)Q_a(s) + Q_b(s) Q_a²(s) + Q_b(s) Q_a³(s)+…+Q_b(s) Q_aⁿ(s)+… =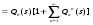

.

Заметим, что выражение в скобках является биномиальным рядом, сходящимся к [1 – Q_a(s)]^-1. Следовательно, окончательная формула эквивалентной функции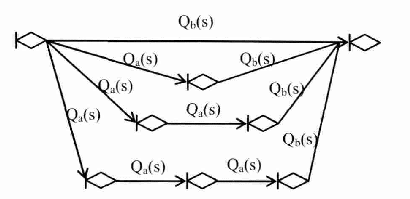



Рис. 5

стохастической сети (рис.4) имеет вид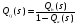

. (18)

Таким образом, мы познакомились с понятием эквивалентной функции стохастической сети, преобразующей исходную сеть, содержащую сколь угодно большое число ветвей к эквивалентной стохастической сети, состоящей из одной ветви. Для получения эквивалентной функции, необходимо представить анализируемый процесс в виде стохастической сети с последующей поэтапной заменой подмножеств ее ветвей эквивалентными, путем использования рассмотренных базовых структур и соответствующих им эквивалентных функций. С целью обобщения приведенных результатовВ дальнейшем рассмотрим основные виды стохастических сетей и основные правила получения для них эквивалентных функций.
Лекция 17.

ВИДЫ СТОХАСТИЧЕСКИХ СЕТЕЙ И ИХ ТИПОВЫЕ СТРУКТУРЫ

Прежде чем приступить к рассмотрению видов стохастических сетей отметим один достаточно очевидный факт. Он состоит в том, что одному и тому же физическому процессу может соответствовать множество адекватных моделей, отличающихся друг от друга степенью детализации анализируемого процесса. Конкретный выбор модели и степень детализации определяется целями и задачами исследования, а также наличием на этапе постановки задачи исходных данных и их полнотой. То есть, входящие в состав стохастической сети элементы могут быть заведомо «не равноправными» и одни ветви могут представлять элементарные (неделимые) случайные процессы, в то время как другие представляют сложные, состоящие из многих элементарных, случайные процессы.

Именно этот факт и приводит к необходимости деления стохастических сетей напростые и сложные.

1. 
   Простые стохастические сети.
   

Стохастическая сеть, состоящая из ветвей описывающих элементарные физические процессы и логических узлов (вершин) одного типа называется простой стохастической сетью.

Как следует из определения, данный вид сетей является достаточно широким. Однако на практике наибольшее применение нашли сети, содержащие логические вероятностные вершины «Исключающее ИЛИ». Это обусловлено тем, что в этом случае стохастическая сеть точно совпадает с определением алгоритма, в котором ветви соответствуют операторам действия, а промежуточные вершины условным операторам. Использование узлов других типов в простых стохастических сетях весьма ограниченно, так как моделирование реального случайного процесса при помощи только логического «И» или «Включающего ИЛИ» затруднительно и приводит, как правило, к сетям, содержащим одновременно несколько типов вершин и не соответствующим данному выше определению.

Очевидно, что целью моделирования процесса функционирования системы связи или ее элементов является получение аналитических выражений для вычисления значений показателей качества и эффективности. Это становится возможным только после определения эквивалентной функции, имеющей физический смысл вероятности реализации исследуемого процесса за время меньшее некоторого времени наступления катастрофы в системе. Под катастрофой понимается такое событие, что система перестает отвечать требованиям к качеству (эффективности) реализуемого ею целевого процесса. При этом поток наступления катастроф является пуассоновским (см. производящие и характеристические функции). Так как целевым процессом, при моделировании систем связи является процесс передачи (доставки) потоков сообщений, то катастрофой в этом случае является факт старения сообщений за время их передачи (доставки) по системе связи.

Понятно, что если сеть состоит из малого числа ветвей и в целом может быть преобразована к одной из базовых структур, то задача определения эквивалентной функции не вызывает никаких трудностей. Однако на практике приходится иметь дело с сетями, сведение которых к базовым достаточно сложно. Примером такой сети является простая стохастическая сеть, содержащая множество контуров (составных петель). Для изучения сетей данного типа введем понятия замкнутой стохастической сети и пели k-го порядка. Предварительно заметим, что петлей первого порядка принято называть петли, не содержащие других петель и позволяющие достичь каждый узел петли из любого другого.

Петлей k-го порядка называется множество k не связанных между собой петель первого порядка.

Эквивалентная функция петли k-го порядка определяется как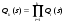

,

где Q_i(s) – эквивалентная функцияi-й петли первого порядка, определяемая как произведение эквивалентных функций ветвей, входящих в эту петлю.

Замкнутой стохастической сетью называется сеть, в которой каждая ветвь принадлежит, по крайней мере, одной петле.

Определение эквивалентной функции стохастической сети, по сути, преобразует исходную сеть в замкнутую. Это позволяет использовать для определения эквивалентной функции исходной сети топологическое уравнение Мейсона для замкнутых графов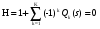

(19)

здесь K – максимальный порядок петель, входящих в стохастическую сеть.

Анализ уравнения показывает, что в него входит и эквивалентная функция исходной стохастической сети, как замыкающая ветвь, образующая петлю первого порядка. Для пояснения рассмотрим сеть рис.6.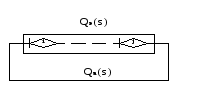



Рис. 6

Данная сеть содержит одну петлю первого порядка с эквивалентной функцией Q(s) = Q_a(s)Q_э(s). Из уравнения Мейсона: 1 - Q_a(s)Q_э(s) = 0 или Q_э(s)= Q_а^-1(s). Важность этого результата состоит в том, что если в топологическом уравнении Q_a(s) заменить на Q_э^-1(s) и решить его относительно Q_э(s), то будет получена искомая эквивалентная функция стохастической сети.

В качестве примера рассмотрим стохастическую сеть рис.7 [17].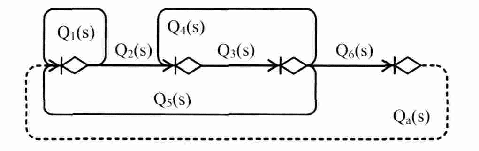



Рис. 7

Чтобы определить эквивалентную функцию Q(s) данной стохастической сети необходимо:

1. 
   Замкнуть стохастическую сеть фиктивной ветвью, исходящей из последнего (выходного) узла и входящей в первый (входящий) узел. На рис.7 эта ветвь показана пунктиром и характеризуется функцией Q_a(s).
   
2. 
   Определить все петли k-го порядка:
   

петлипервогопорядка:

Q₁(s); Q₃(s)Q₄(s); Q₂(s)Q₃(s)Q₅(s); иQ₂(s)Q₃(s)Q₆(s)Q_a(s);

петля второго порядка:

Q₁(s)Q₃(s)Q₄(s).

3. 
   С использованием топологического уравнения определить эквивалентную функцию сети.
   

Помня, что Q(s) = [Q_а(s)]^-1из топологического уравнения получаем

H=1-Q₁(s)-Q₃(s)Q₄(s)-Q₂(s)Q₃(s)Q₅(s)-Q₂(s)Q₃(s)Q₆(s)Q^-1(s)+ Q₁(s)Q₃(s)Q₄(s)=0.

Отсюда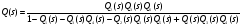

.

Искомая эквивалентная функция найдена.

При определении эквивалентной функции мы полагали, что случайные времена реализации ветвей являются независимыми. В противном случае, необходимо обусловить преобразование Лапласа той ветви, для которой время ее реализации является зависимым, то есть [17]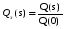



Таким образом, если имеется простая стохастическая сеть, состоящая из параллельных, последовательных цепей и петель, то при помощи топологического уравнения и использования базовых структур она может быть преобразована в эквивалентную сеть, содержащую единственную ветвь, характеризуемую эквивалентной функцией сети.

Сложные стохастические сети.

Стохастическая сеть, состоящая из ветвей, представляющих в данной сети сложные (композиционные) процессы и/или содержащая различные типы логических узлов (вершин) называется сложной.

Как следует из определения, возможны следующие виды сложных стохастических сетей:

• 
  сеть содержит узлы одного типа, но ветви представляют композиционные случайные процессы. Сложные стохастические сети данного вида называются укрупненными и находят наиболее широкое применение;
  
• 
  сеть содержит несколько типов вершин, предусматривающих реализацию различных логических операций. При этом, ветви представляют элементарные (неделимые) процессы. Такие сети называются смешанными;
  
• 
  сеть содержит несколько типов вершин, а ветви представляют композиционные процессы. Сети данного вида будем называть укрупненными смешанными сетями.
  

Основной особенностью укрупненных сетей является то, что их ветви характеризуются эквивалентными функциями, полученными, как правило, из простых стохастических сетей. Поэтому для получения эквивалентной функции укрупненной стохастической сети используются те же правила, что и для простых сетей. Это позволяет говорить о вложенности разрабатываемых моделей и дает возможность проведения поэтапного (поэлементного) анализа исследуемой системы и процесса ее функционирования. Поэтапность моделирования может существенно облегчить и решение задач синтеза системы по показателям, определяемым из эквивалентной функции. Кроме того, это позволяет анализировать качество функционирования системы связи с точки зрения системы управления силами и оружием. Более подробно эти вопросы будут рассматриваться в другом разделе.

Если анализируемый процесс представлен в виде смешанной стохастической сети, безусловное использование изложенного выше подхода, для определения эквивалентной функции, не является правомочным. Поэтому, на первом этапе анализа сети производится преобразование узлов «Включающее ИЛИ» и «И» в узлы типа «Исключающее ИЛИ». А затем, используя выше приведенные правила определяют эквивалентную функцию стохастической сети. То же касается и укрупненных смешанных сетей. Так как указанное преобразование узлов является общим для двух видов сложных сетей, то рассмотрим его более подробно.

Преобразование узлов «И» и «Включающее ИЛИ» производится на основе следующих утверждений:

1. 
   Все узлы работают так, как если бы в один момент времени реализовалась одна и только одна входящая в узел ветвь и только одна ветвь являлась исходящей. Это означает, что при последовательном соединении ветвей вид узла не оказывает влияния на эквивалентную функцию;
   
2. 
   Понятие петли применяется только для узлов «Исключающее ИЛИ». Это обусловлено тем, что петля реализуется только после прямой ветви и исключает возможность их одновременной реализации, предусматриваемой логической операцией «И». Однако, по той же причине, в общем случае, узел «Включающее ИЛИ» может быть заменен на узел «Исключающее ИЛИ»;
   
3. 
   Множество взаимно исключающих путей стохастической сети является счетным.
   

С учетом перечисленных утверждений рассмотрим стохастическую сеть, содержащую узлы типа «И», (рис.8).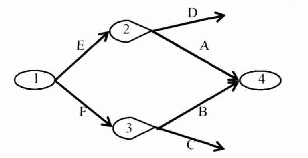



Рис. 8

Узел 4 будет реализован только в том случае, когда будут реализованы узлы 1, 2 и3, а также ветви E, F, A и B. Положим, что вероятности реализации узлов 1,2 и 3 соответственно равны 1, а вероятности выбора ветвей равны: p_A; p_B; p_D = 1- p_A, p_C = 1 - p_B; p_E = p_F =1. При этом, случайные времена реализации ветвей составляют: t_A; t_B; t_C; t_D; t_E = t_F = 0.

Отсюда, вероятность реализации узла 4, а значит и сети в целом:

P_AB = p_Ap_B ,

а время ее реализации определяется из условия

t_p= max(t_A, t_B) = .

Полагая, что ветви A и B имеют эквивалентные функции Q_A(s) и Q_B(s), с использованием теоремы упреждения (см. свойства преобразований Лапласа [5]) получим эквивалентную функцию сети (рис.8)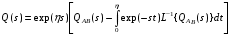

, (20)

Где: символ L^-1{*} соответствуетоперации обратного интегрального преобразования;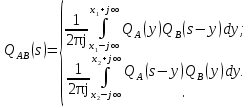


Результат ф(20) позволяет поставить в соответствие узлу «И» узел «Исключающее ИЛИ» и может быть обобщен на любое число входящих в узел «И» ветвей.

В частном случае, когда время реализации ветвей А и В характеризуются экспоненциальным законом распределения, т.е.



эквивалентная функция сети (рис. 8) имеет вид: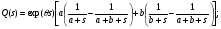



где: a=1/t_A; b=1/t_B; ϴ=1/(a+b).

Рассмотрим теперь стохастическую сеть, содержащую узел «Включающее ИЛИ» (рис.9) и определим времена и вероятности реализации взаимно исключающих ветвей:

1. 
   Вероятность реализации только ветви A, входящей в узел 4 равна
   

P_A = p_A –p_AB = p_A - p_Ap_B,

а время ее реализации равно t_A;

2. 
   Вероятность реализации только ветви B, входящей в узел 4 равна
   

P_B = p_B –p_AB = p_B - p_Ap_B,

а время ее реализации равно t_B;

3. 
   Вероятность совместной реализации ветвей A и B равна
   

P_AB = p_AB = p_Ap_B,

а время реализации составляет t_p= min(t_A, t_B).

Тогда, стохастическая сеть, эквивалентная исходной (рис.9) примет вид (рис.10).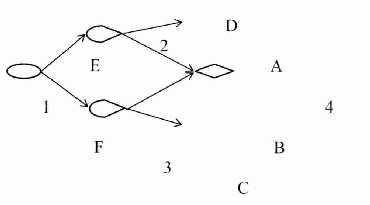



Рис. 9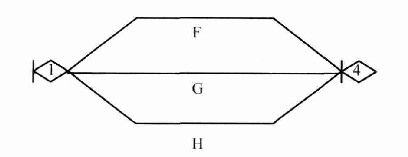


Рис. 10

Ветви стохастической сети (рис.10) имеют эквивалентные функции:

Q_F(s) = Q_A(s) – Q_A(s)Q_B(s);

Q_G(s) = Q_B(s) – Q_A(s)Q_B(s);

Q_H(s) = Q_A(s)Q_B(s)exp{-s},

а значит эквивалентная функция сети в целом имеет вид (см.ф.17)

Q(s) = Q_A(s) + Q_B(s) – Q_AВ(s)],

где:t_p= min(t_A, t_B);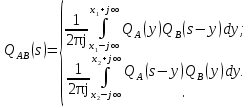




Комплексные интегралы в правой части распространяются вдоль вертикальных прямых в комплексной плоскости. При этом в первом интеграле точку х₁ на вещественной оси и комплексную точку s следует взить настолько далеко вправо, чтобы для точки y, перемещающейся вдоль вертикальной прямой, соединяющей точки (х₁-∞) и (х₁+∞), соблюдались два условия: чтобы у оставалась в полуплоскости сходимости изображения L{Q_A(s)}, и чтобы s-yоставалось в полуплоскости сходимости изображения L{Q_В(s)}. То же относится и ко второму интегралу.

В частном случае, когда время реализации ветвей А и В характеризуются экспоненциальным законом распределения, т.е.



эквивалентная функция сети (рис. 9) имеет вид: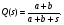



Таким образом, при наличии в стохастической сети различных видов узлов их необходимо преобразовать в узлы «Исключающее ИЛИ», составить эквивалентную стохастическую сеть, а затем определить ее эквивалентную функцию.