Методологические основы моделирования
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
Зависимость разведзащищённости от степени неоднородности сетейКоличественная мера неоднородности, механизм получения графических последовательностей с различной степенью неоднородности и алгоритмы построения эталонных графов по этим последовательностям рассмотрены ранее. Множество графических степенных последовательностей Пi вместе с соответствующими характеристиками приведены в таблице2. Полученные результаты исследования приведены на рис.10. и на первый взгляд, кажутся неожиданными и даже противоестественными, поскольку однородные структуры распознаются с большей вероятностью, чем неоднородные при одинаковой вероятности обнаружения ребра. i=1 i=16 i=7 i=8 Рис.9. Графы последовательностей 1,7,8 и 16 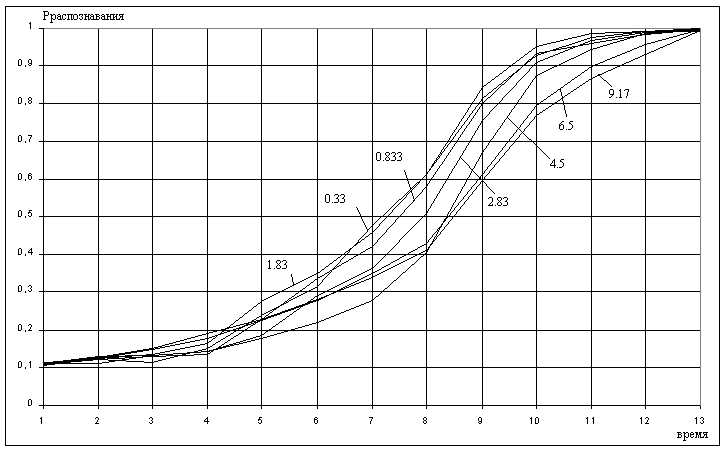 Рис.10. Графики зависимости вероятности распознавания от времени и от дисперсии степени вершин Причина этого заключается в том, что алгоритм распознавания изоморфности прекращает работу, как только одна из реализаций случайного розыгрыша становится изоморфной или изоморфно вкладывается в граф-эталон . Однако, с уменьшением степени неоднородности графа возрастает число автоморфизмов графа, т.е. число изоморфизмов графа на себя. Теоретически число вариантов построения графа определяется числом групп с одинаковыми степенями вершин и числом таких вершин, входящих в группу: 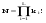 , , 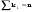 , 1≤ L ≤ n , 1≤ L ≤ nгде N- число вариантов построения графа; n- число вершин графа; L- число групп вершин с одинаковыми степенями; ki- число вершин в группе. При L=N , т.е. когда количество различимых групп равно количеству различимых вершин, (все вершины имеют разные степени) существует всего один вариант построения графа. При L=1, N=n!. Реальное число вариантов ограничивается особенностями алгоритма построения графа по заданной графической последовательности. Максимальное число вариантов получается когда di=6. Покажем пример подсчета числа вариантов для последовательности с наибольшим числом вариантов. vi1 2 3 4 5 6 7 8 9 10 11 12 di 6 6 6 6 6 6 6 6 6 6 6 6 П16 Первую вершину можно выбрать 12 способами, далее нужно выбрать 6 вершин из оставшихся 11. Это можно сделать 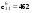 , таким образом первый шаг можно выполнить 12.462=5444 способами. , таким образом первый шаг можно выполнить 12.462=5444 способами.Второй шаг: vi8 9 10 11 12 2 3 4 5 6 7 1 di 6 6 6 6 6 5 5 5 5 5 5 0 Первую вершину можно выбрать 5 способами, порядок следующих 4х, имеющих степень 6 не играет роли. 6, 7-ю вершину со степенью 5 можно выбрать одним из 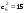 способов, таким образом второй шаг можно сделать 15х5 =75 способами. способов, таким образом второй шаг можно сделать 15х5 =75 способами.Третий шаг: vi9 10 11 12 4 5 6 7 2 3 1 8 di 5 5 5 5 5 5 5 5 4 4 0 0 Первую вершину можно выбрать 8-ю способами, вторую группу вершин (5) можно выбрать 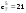 способом, таким образом третий шаг можно выполнить 8х21=168 способами. способом, таким образом третий шаг можно выполнить 8х21=168 способами.Четвертый шаг: vi6 7 10 11 12 4 5 2 3 1 8 9 di 5 5 4 4 4 4 4 4 4 0 0 0 Первую вершину можно выбрать 2-мя способами, вторую группу вершин (со степенью di =4) можно выбрать 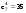 способами, таким образом четвертый шаг можно выполнить 2х35=70 способами. способами, таким образом четвертый шаг можно выполнить 2х35=70 способами.Пятый шаг: vi7 5 2 3 10 11 12 4 1 8 9 6 di 4 4 4 4 3 3 3 3 0 0 0 0 Первую вершину можно выбрать 4-мя способами, вторую группу вершин (со степенью di =3) можно выбрать 4 способами, таким образом четвертый шаг можно выполнить 4х4=16 способами. Шестой шаг: vi5 2 3 11 12 4 10 1 8 9 6 7 di 3 3 3 3 3 3 0 0 0 0 0 0 Первую вершину можно выбрать 6-ю способами, вторую группу вершин (со степенью di =3) можно выбрать 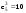 способами, таким образом шестой шаг можно выполнить 6х10=60 способами. способами, таким образом шестой шаг можно выполнить 6х10=60 способами.Седьмой шаг: vi12 4 10 2 3 11 1 8 9 6 7 5 di 3 3 2 2 2 2 0 0 0 0 0 0 Первую вершину можно выбрать 2-мя способами, вторую группу вершин (со степенью di =2) можно выбрать 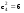 способами, таким образом седьмой шаг можно выполнить 6х2=12 способами. способами, таким образом седьмой шаг можно выполнить 6х2=12 способами.Восьмой шаг: vi4 3 11 10 2 1 8 9 6 7 5 12 di 2 2 2 1 1 0 0 0 0 0 0 0 Первую вершину можно выбрать 3-мя способами, восьмой шаг может быть выполнен 3 способами. Девятый шаг: vi3 11 10 2 1 8 9 6 7 5 12 4 di 1 1 1 1 0 0 0 0 0 0 0 0 Первую вершину можно выбрать 4-мя способами, девятый шаг также может быть выполнен 4-мя способами. Десятый шаг: vi10 2 3 4 5 6 7 1 8 9 11 12 di 1 1 0 0 0 0 0 0 0 0 0 0 Десятый шаг –соединение 10 и 2 вершины, можно выполнить 2-мя способами, однако, поскольку графы не ориентированы, то порядок соединения не играет роли, поэтому число вариантов 10-го шага –1. Общее число вариантов равно сумме вариантов на каждом шаге, таким образом для последовательности П16 существует 5953 изоморфных графа. Число вариантов для других последовательностей показано в таблице 1. Изоморфность графов проверялось по ходу их построения. Таким образом, графики на рис.3 необходимо интерпретировать как вероятность распознавания хотя бы одного из изоморфных графов, построенных по графической последовательности, обладающей заданной степенью неоднородности. Вероятность распознавания конкретной структуры Ркс по полученной вероятности распознавания типовой структуры Ртс, можно получить из следующего соотношения: РТС=1-(1-РКС)N, откуда 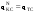 , или , или 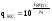 , или , или 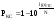 . Графки для пересчета РТС в РКС в зависимости от числа вариантов показаны на рис.11. . Графки для пересчета РТС в РКС в зависимости от числа вариантов показаны на рис.11.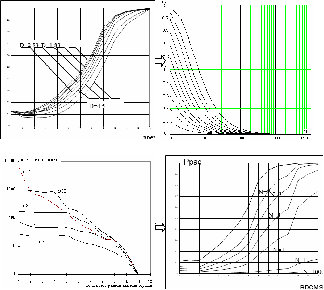 Рис. 11. Графики нахождения вероятности распознавания конкретной структуры При N=1, соответственно lgN=0, РТС = РКС . для того, чтобы получить значение РКС , необходимо иметь с графика рис.3 значение РТС , определить из таблицы №1 значение N и по этим двум параметрам с графики рис.4 снять значение РКС. 5. Синтез сетей связи, оптимальных по показателям структурной устойчивости и разведзащищенности. Традиционно считается, что показатели устойчивости и разведзащищенности систем( сетей )связи в принципе являются антагонистическими, т.е. увеличение одного приводит к снижению другого и наоборот. Именно поэтому синтез сетей связи производят, как правило, по одному из этих двух показателей, а на другой накладывают допустимые ограничения. Такой подход вполне правомерен тогда, когда скрываются отдельные объекты, элементы сети связи. В тех случаях, когда объектом скрытия является конкретная информационная сеть, предназначенная для обеспечения решения конкретной оперативно- тактической задачи, а основными путями скрытия являются унификация сигналов радиосвязи и структур сетей, возможна другая подстановка задачи и ее решения, когда оба показателя можно улучшать одновременно. В основе этого решения лежит создание однородных k- связных сетей, которые, как показано ранее, обладают и наибольшей устойчивостью и наибольшей разведзащищенностью.  Полученные зависимости структурной разведзащищенности от степени неоднородности для одинаковых значений весовых коэффициентов ребер приведены на рис.12. Полученные зависимости структурной разведзащищенности от степени неоднородности для одинаковых значений весовых коэффициентов ребер приведены на рис.12.Рис. 12 . Графики зависимости показателей структурной живучести и разведзащищенности от степени неоднородности сети. Следует еще раз обратить внимание на то, что под распознаванием состава и структуры сети имеется в виду распознавание состава сети и установление кто, с кем , какими каналами связан, а не только то, что сеть состоит из 12 корреспондентов и имеет сотовую структуру. Различие между понятиями типовой и конкретной структуре были подробно установлены на основе понятия автоморфизма. Естественно возникает вопросы, что же при этом теряется, ухудшается, за счет чего это происходит, какова цена решения, при каких ограничениях и допущениях возможна реализация такого решения. Во-первых, чтобы разведзащищенность не снижалось, предполагается, что интенсивность исходящих потоков остается неизменной при переходе к k- связным структурам. Во-вторых это означает, что если раньше был один канал с пропускной способностью С, то теперь она делится на k частей, что может привести к уменьшению времени доставки сообщений, либо число каналов увеличивается в k-раз, что увеличивает стоимость. Во-третьих, это требует перехода к пакетным радиосетям, что приводит к развитию алгоритмов управления потоками на сетях, а это открывает широкую дорогу для проведения дальнейших исследований. Лекция 13. МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ Случайная величина позволяет представить поведение изменяющегося случайным образом сигнала в определенный момент времени. Однако при проектировании целого ряда систем связи важно учитывать изменение случайных сигналов не только по уровню, но и по времени. В качестве моделей случайных сигналов и помех, позволяющих отразить их динамические характеристики, используются случайные процессы (СП), представляющие собой случайные функции времени. При этом конкретный вид, который принимает СП в отдельном эксперименте, называется реализацией СП [4, 6]. 3.1. Моделирование марковских случайных процессов Во многих радиотехнических приложениях СВ (х1, х2, ..., хn) связаны со значениями непрерывного процесса х(t) в моменты времени t1, t2, ..., tn, т.е. х1 = х(t1), х2 = х(t2), ..., хn =  х(tn). В этом случае упорядоченная система непрерывных СВ х1, х2, ..., хn (рис.3.1) называется случайной последовательностью, которую можно также интерпретировать как реализацию СП в данном опыте [5]. х(tn). В этом случае упорядоченная система непрерывных СВ х1, х2, ..., хn (рис.3.1) называется случайной последовательностью, которую можно также интерпретировать как реализацию СП в данном опыте [5].Простейшее вероятностное описание СП соответствует независимым СВ х1, х2, ..., хn, тогда совместная ПРВ w(х1, х2, ..., хn) = 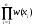 . Однако последовательность независимых СВ представляет собой ММ довольно узкого класса реальных процессов. Действительно с помощью СП с независимыми значениями невозможно дать описание "гладких", коррелированных помех или медленно изменяющихся параметров полезных сигналов, например, координат радиолокационных целей. Поэтому во многих задачах необходимо использовать модели СП с зависимыми значениями. В общем случае совместная ПРВ таких СП определяется по формуле . Однако последовательность независимых СВ представляет собой ММ довольно узкого класса реальных процессов. Действительно с помощью СП с независимыми значениями невозможно дать описание "гладких", коррелированных помех или медленно изменяющихся параметров полезных сигналов, например, координат радиолокационных целей. Поэтому во многих задачах необходимо использовать модели СП с зависимыми значениями. В общем случае совместная ПРВ таких СП определяется по формуле w(х1, х2, ..., хn) = w(х1) w(х2/х1) w(х3/х1, х2) ... w(хn/х1, х2, ..., хn-1). w(х1, х2, ..., хn) = w(х1) w(х2/х1) w(х3/х1, х2) ... w(хn/х1, х2, ..., хn-1).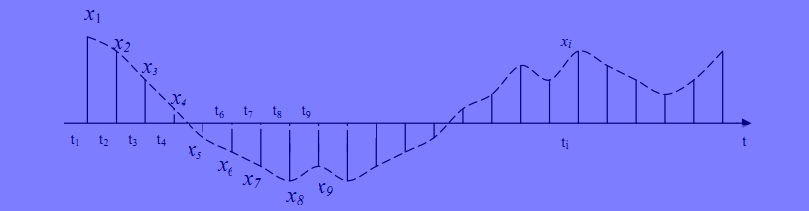 Рис.3.1 Случайная последовательность Математические трудности применения этой формулы для вероятностных расчетов быстро нарастают с увеличением n. В связи с этим необходимо из всех возможных СП с зависимыми значениями выделить класс СП, имеющих относительно простое математическое описание. Очевидно, наиболее простые соотношения для ПРВ получатся, если положить w(хi/х1, х2, ..., хi-1) = w(хi/ хi-1). (3.1) Это равенство означает, что условная ПРВ и, следовательно, любые другие вероятностные характеристики СП до момента времени ti являются функциями только значения хi-1, принятого СП в предшествующий момент времени. Случайные последовательности, удовлетворяющие (3.1), называются марковскими по имени русского математика А.А.Маркова, разработавшего основы теории таких СП. Марковская последовательность называется однородной, если условные ПРВ w(хi/хi-1), называемые ПРВ перехода, не зависят от i. Марковская последовательность называется стационарной, если она однородна и все состояния хi имеют одну и ту же безусловную ПРВ w(х). При моделировании марковских СП для формирования на ЭВМ случайных чисел с заданным законом распределения могут быть использованы методы, рассмотренные выше. В более общем случае рассматриваются N-связные марковские процессы, т.е. N взаимосвязанных между собой процессов х1(t), …, хn(t), в совокупности обладающих марковскими свойствами [1, 4, 11]. Эти процессы характеризуются условной ПРВ перехода, которая имеет вид: w(х1, n, …, хN, n, tn׀х1,n-1, …, хN, n-1, tn-1) = w0(х1, n, …, хN, n, х1, n-1, …, хN, n-1, tn, tn-1). Моделирование N-связных марковских процессов по заданной условной ПРВ перехода в принципе не отличается от моделирования рассмотренных выше одномерных (простейших) марковских процессов, однако получение N-связных дискретных реализаций с ростом N усложняется. Другим обобщением одномерных марковских процессов являются одномерные марковские процессы N-го порядка, отличающиеся от простейших марковских процессов тем, что ПРВ перехода в очередное состояние зависит не от одного, а от N предшествующих состояний. Стохастическое уравнение хi = φ(хi-N, хi-N+1, …, хi-2, хi-1, ξi) при соответствующих начальных условиях порождает марковский процесс N-го порядка, который можно рассматривать как компоненту N-связного марковского процесса, поэтому моделирование марковских процессов N-го порядка может быть сведено к моделированию N-связных марковских процессов. Выше шла речь о моделировании марковских процессов общего вида: на характеристики процессов не накладывалось других ограничений, кроме указанных выше. Распространенными являются марковские процессы, которые удовлетворяют дополнительны условиям, чаще всего, условию нормальности распределения, стационарности (однородности), а также условию нормальности и стационарности одновременно. В этих случаях моделирование марковских процессов упрощается. Действительно, у стационарных марковских СП ПРВ перехода вида w(хn, tn׀хn-1, tn-1, …, х1, t1) = w(хn, tn׀хn-1, tn-1) = w0(хn, хn-1, tn, tn-1), w(х1, n, ..., хN, n, tn׀х1, n-1, …, хN, n-1, tn-1) = w0(х1, n, …, хN, n, х1, n-1, …, хN, n-1, tn, tn-1) зависит лишь от разности ∆tn = tn - tn-1. Это упрощает процесс моделирования (в особенности для одномерных марковских процессов), так как уменьшается число аргументов функции w0(хn, хn-1, tn, tn-1), которую требуется хранить в памяти ЭВМ при моделировании. Как уже отмечалось, наиболее полное описание стационарных СП дает многомерная ПРВ. Однако этот подход требует большого количества информации. Для описания негауссовских СП используются различные преобразования гауссовских процессов и марковские процессы. Реальные СП можно с требуемой точностью аппроксимировать многомерными марковскими процессами [44]. Действительно [1, 38], любой СП, спектральная плотность которого является дробно-рациональной функцией частоты, является компонентой многомерного марковского процесса. 3.2. Разностные и дифференциальные стохастические уравнения Одним из достоинств марковских процессов является возможность их описания с помощью стохастических ДУ. Для этого вводится понятие формирующей динамической системы. При этом СП характеризуется параметрами линейных или нелинейных фильтров, на вход которых подается белый гауссовский шум или другое известное возмущение [32]. Так как любая динамическая система может быть описана ДУ, то и СП на ее выходе так же  может быть описан стохастическим ДУ соответствующего порядка. может быть описан стохастическим ДУ соответствующего порядка.Модели СП в виде стохастических ДУ обладают рядом положительных свойств. Прежде всего, в отличие от других методов описания СП (например, с помощью ПРВ или моментных функций), они непосредственно определяют способ генерации его реализаций, для осуществления которого можно вполне успешно использовать аналоговые вычислительные устройства или соответствующие программы для ЭВМ. Использование стохастических ДУ в форме уравнений состояния позволяют синтезировать алгоритмы оптимальной обработки и генерации для широкого класса сигналов и помех [16, 32, 44]. Для большинства реальных СП используется модель в виде ДУ, линейных относительно входных воздействий типа белого шума 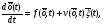 где 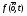 - векторная и - векторная и 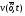 - матричная функции векторного аргумента [16, 44]; - матричная функции векторного аргумента [16, 44]; 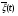 - белый гауссовский шум с нулевым математическим ожиданием и заданной корреляционной функцией (КФ). Задавая различные функции - белый гауссовский шум с нулевым математическим ожиданием и заданной корреляционной функцией (КФ). Задавая различные функции 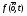 и и 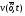 в уравнении (3.2), можно получить СП с различными статистическими характеристиками. Так, если в уравнении (3.2), можно получить СП с различными статистическими характеристиками. Так, если 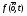 - линейная функция, а - линейная функция, а 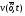 не зависит от не зависит от 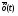 , то уравнение (3.2) будет определять гауссовский СП. В работах [16, 38] приведены связи между функциями , то уравнение (3.2) будет определять гауссовский СП. В работах [16, 38] приведены связи между функциями 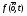 , , 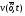 и соответствующими статистическими характеристиками (ПРВ, КФ). и соответствующими статистическими характеристиками (ПРВ, КФ).Следует отметить, что задача синтеза марковской модели СП, т.е. определение функций 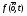 и и 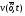 по заданным статистическим характеристикам, не всегда имеет одно решение. Здесь возникает вопрос о единственности решения. Если заданы статистические характеристики моделируемого процесса в форме функций распределения, то можно указать несколько уравнений различных типов, порождающих процессы с такими характеристиками. В случае нелинейных моделей это является неизбежным следствием ограниченности исходных сведений о процессе. Если единственное решение задачи синтеза отсутствует, то при выборе уравнения, которое будет заложено в основу функционирования какого-либо устройства, можно учитывать соображения сложности, экономичности и так далее. На практике число эквивалентных, с точки зрения статистических характеристик, уравнений обычно не велико (не более трех, четырех), и из них всегда можно выбрать единственное [32]. по заданным статистическим характеристикам, не всегда имеет одно решение. Здесь возникает вопрос о единственности решения. Если заданы статистические характеристики моделируемого процесса в форме функций распределения, то можно указать несколько уравнений различных типов, порождающих процессы с такими характеристиками. В случае нелинейных моделей это является неизбежным следствием ограниченности исходных сведений о процессе. Если единственное решение задачи синтеза отсутствует, то при выборе уравнения, которое будет заложено в основу функционирования какого-либо устройства, можно учитывать соображения сложности, экономичности и так далее. На практике число эквивалентных, с точки зрения статистических характеристик, уравнений обычно не велико (не более трех, четырех), и из них всегда можно выбрать единственное [32]. В последнее время, в связи с широким использованием цифровых устройств в радиотехнических системах для статистического описания сигналов и помех используют случайные последовательности, которые могут быть заданы разностными стохастическими уравнениями 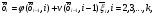 (3.3) (3.3)где 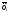 - состояние системы в момент времени ti; - состояние системы в момент времени ti; 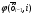 - векторная функция; - векторная функция; 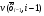 - матричная функция; - матричная функция; 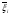 - последовательность СВ [32, 33]. Если в качестве возбуждающей последовательности - последовательность СВ [32, 33]. Если в качестве возбуждающей последовательности 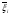 использовать дискретный белый шум, то уравнение (3.3) будет определять марковскую последовательность. использовать дискретный белый шум, то уравнение (3.3) будет определять марковскую последовательность.При использовании стохастических уравнений (3.1), (3.3) в качестве моделей случайных сигналов и помех возникают задачи анализа и синтеза [38]. Первая из них заключается в определении статистических характеристик (в первую очередь ПРВ и КФ) СП или случайной последовательности по заданным функциям f, v и φ по заданным статистическим характеристикам. Для непрерывных СП обе эти задачи решены для достаточно большого числа частных случаев [8, 16, 23]. При этом анализ выполняется на основе решения уравнения Фоккера-Планка-Колмогорова [44]. Для случайных последовательностей эти задачи до конца решены лишь для случая линейной функции 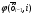 и независящей от и независящей от 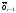 функции v [5]. Кроме того, в работах [32, 38, 44] рассмотрено решение задачи синтеза и для нелинейной функции. Однако при этом накладываются ограничения на вид ПРВ. Отсутствие конструктивных решений задачи синтеза, применительно к разностному уравнению (3.3), не позволяет получить ММ случайных последовательностей с заданными статистическими свойствами. функции v [5]. Кроме того, в работах [32, 38, 44] рассмотрено решение задачи синтеза и для нелинейной функции. Однако при этом накладываются ограничения на вид ПРВ. Отсутствие конструктивных решений задачи синтеза, применительно к разностному уравнению (3.3), не позволяет получить ММ случайных последовательностей с заданными статистическими свойствами. |
