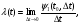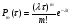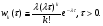Методологические основы моделирования
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
Лекция 14 МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПОТОКОВ И СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ Системы массового обслуживания ( СМО) отражают процессы функционирования многих современных сложных систем. Теория массового обслуживания получила свое первоначальное развитие благодаря запросам телефонии при изучении процесса загрузки телефонной станции. Примеры СМО: телефонные станции, билетные кассы, системы организации транспорта (грузоперевозки, поток автомобилей через мост) и т. п. Каждая такая система состоит из некоторого количества обслуживающих единиц: «каналов» обслуживания (например, линии связи). Работа любой СМО состоит в обработке (обслуживании) поступающего на нее потока требований или заявок. Заявки поступают одна за другой в случайные моменты времени. Обслуживание поступившей заявки продолжается какое-то время, после чего канал освобождается и может принимать следующую заявку. Каждая СМО, в зависимости от числа каналов и их производительности, обладает некоторой пропускной способностью, позволяющей ей более или менее успешно справляться с потоком заявок. Под пропускной способностью в узком смысле слова обычно понимают среднее число заявок, которое система может обслужить в единицу времени. Случайный характер потока заявок приводит либо к отказам, либо к образованию очередей. На случайности, связанные с характером потока заявок, накладывается еще случайное время обслуживания отдельных заявок в каналах СМО. Таким образом, предметом теории массового обслуживания является установление зависимостей между характером потока заявок, производительностью отдельных каналов, числом каналов и показателями эффективности обслуживания. 5.1. Модели случайных потоков 5.1.1. Виды потоков и способы их задания В теории массового обслуживания вводится в рассмотрение модель потока событий. Потоком событий называется последовательность событий, следующих одно за другим в случайные моменты времени t1,t2,...,tk,...(рис. 5.1). Потоки событий, происходящих в случайные моменты времени t1,t2 >t1 ,...,tn >tn−1,...,являются специфичным классом СП. Они используются в качестве ММ при исследовании СМО, в задачах приема импульсных сигналов, в задачах надежности и др. На рис. 5.1 изображена одна реализация потока событий. При этом в качестве событий могут быть, например, заявки на входе СМО и заявки на выходе СМО. 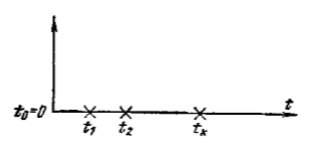 Рис. 5.1. Поток событий 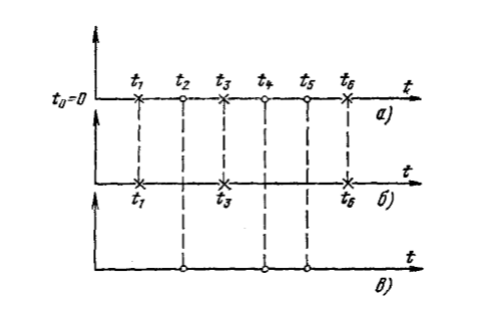 Рис. 5.2. Неоднородный поток событий а – составной неоднородный поток; б, в – составляющие однородные потоки Потоки заявок могут быть однородными и неоднородными. В неоднородном потоке события, образующие поток, могут относиться к различным типам. Схематично неоднородный поток событий может быть изображен в виде рис. 5.2, где кружочками и крестиками изображаются однородные потоки событий. Возможны различные эквивалентные способы задания случайных потоков. Наиболее общим способом представления характеристик потоков является задание многомерной ПРВ интервалов между моментами наступления событий w(1,...,n), гдеtktk,t00. При таком задании случайных потоков моделирование сводится к формированию на ЭВМ реализаций случайных чисел 1,2,...,nс законом распределения w(1,...,n). Случайные потоки общего вида редко встречаются в приложениях. Обычно рассматриваются более узкие модели, например, потоки с ограниченным последействием, у которых интервалы 1,...,nмежду событиями статистически независимы в совокупности, т. е.
Эти потоки задаются последовательностью одномерных законов распределения wk,k1,2,... Поток называется регулярным, если события следуют одно за другим через строго определенные промежутки времени. В реальных СМО поток заявок обычно является случайным. Такие потоки характеризуются следующими тремя свойствами.
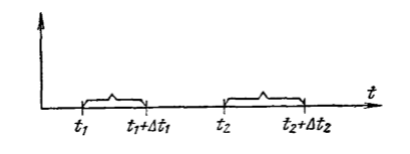 Рис. 5.3. Интервалы времени для определения последействия потока
5.1.2. Простейший поток Если поток событий обладает тремя названными свойствами, то он называется простейшим ( или стационарным пуассоновским) потоком. Простейший поток играет среди потоков событий особую роль, до некоторой степени близкую к роли нормального закона среди других законов распределения. Можно доказать, что при суммировании (взаимном наложении) большого числа ординарных, стационарных потоков с последействием получается поток близкий к простейшему. Пусть имеется ряд независимых потоков 1,2,...,n, имеющих одинаковое распределение. «Суммирование» потоков состоит в том, что все моменты появления событий переносятся на одну и ту же ось времени Ot. Рассмотрим на оси Ot два неперекрывающихся отрезка (рис. 5.3). Каждая из точек, попадающих в эти отрезки, случайным образом может оказаться принадлежащей тому или иному потоку, и по мере увеличения n удельный вес точек, принадлежащих одному и тому же потоку ( и, значит, зависимых), уменьшается, а остальные точки принадлежат разным потокам и появляются на отрезках независимо друг от друга. При увеличении n суммарный поток будет терять последействие и приближаться к простейшему. На практике достаточно сложить 4-5 потоков, чтобы получить поток, достаточно близкий к простейшему. Важной характеристикой является интенсивность потока, определяемая как предел
где 1t0,∆ t)— вероятность того, что на интервале (t0,t0∆ tпоявятся одна или более заявок. Для стационарного потока его интенсивность не зависит от времениλ (t ) =λ и равна среднему числу событий в единицу времени. Рассмотрим на оси Ot простейший поток событий. Выделим произвольный участок времени длиной τ. Число точек m, попадающих на участок τ, распределено по закону Пуассона
В частности, вероятность того, что не произойдет ни одного события Pexp; вероятность появления ровно одного события P1e. Важной характеристикой потока является закон распределения случайного интервала T между соседними событиями. Функция распределения FPTдля простейшего потока находится следующим образом: 1FPT=P0expиF(1exp,0. Дифференцируя F (τ) , найдем ПРВ интервалов между событиями простейшего потока:
Математическое ожидание интервала T, распределенного по показательному закону mM1/, а дисперсия DD1/2. Следует заметить, что кроме характеристик входного потока заявок, режим работы СМО зависит еще от характеристик производительности самой системы: числа каналов n и быстродействия каждого канала. Одной из важнейших величин, связанных с системой, является время обслуживания одной заявки T об . Рассмотрим СВTоб и обозначим Fобtее функцию распределения: FобtPTобt, а wобt)F об(t- ПРВ. Для практики особый интерес представляет случай, когда величина об T имеет показательное распределение wобt)µeµt,t0, где параметр µ=1/mtоб называетсяинтенсивностьюобслуживания.Как известно параметр λ имеет смысл «плотности потока заявок». Аналогично, величину µ можно характеризовать как «плотность потока освобождений» занятого канала. Представим себе канал, непрерывно занятый (бесперебойно снабжаемый заявками); тогда очевидно, в этом канале будет иметь место простейший поток освобождений с плотностью µ. 5.1.3. Потоки с ограниченным последействием Рассмотрим ординарный стационарный поток однородных событий с последействием. Такой поток называется потоком Пальма, если промежутки времени 1,2,...,между последовательными событиями представляют собой независимые СВ, подчиняющиеся в общем случае закону распределения, отличающемуся от (5.4). Потоки Пальма часто получаются в виде выходных потоков СМО. Если на какую-либо СМО поступает поток заявок, то он этой системой разделяется на два: поток обслуженных заявок и поток необслуженных заявок, который, в свою очередь, поступает на какую-либо другую СМО. Теорема Пальма: пусть на СМО поступает поток заявок типа Пальма, причем заявка, заставшая все каналы занятыми, получает отказ (не обслуживается); если при этом время обслуживания имеет показательный закон распределения, то поток необслуженных заявок также является потоком Пальма. В частности, если входной поток заявок будет простейшим, то поток необслуженных заявок, не будучи простейшим, будет все же иметь ограниченное последействие. Потоки, у которых w1w,определяются единственным законом распределения w,и называются рекуррентными (стационарными) потоками. Потоки с ограниченным последействием, у которых 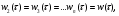 , называются рекуррентными потоками с запаздыванием. Они задаются двумя законами распределения w1и w. Здесь wхарактеризует ПРВ временного интервала между i-й и i1-й заявками. , называются рекуррентными потоками с запаздыванием. Они задаются двумя законами распределения w1и w. Здесь wхарактеризует ПРВ временного интервала между i-й и i1-й заявками. Рассмотрим моделирование потоков с ограниченным последействием. Для получения реализаций последовательности моментов наступления событий tk,k1,2,...,достаточно сформировать последовательность реализаций k,k1,2,..., СВ с заданными законами распределения wkсоответственно и вычислить моменты наступления событий: tktk1k. Моделирование рекуррентных потоков упрощается еще и тем, что СВk имеют одинаковый закон распределения. 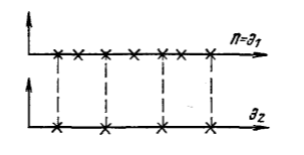 Рис. 5.4. Получение потока Эрланга путем просеивания простейшего потока Пример потоков с ограниченным последействием – потоки Эрланга, которые образуются «просеиванием» простейшего потока (рис. 5.4). Если в простейшем потоке выбросить каждую вторую точку, то оставшиеся точки образуют поток, называемый потоком Эрланга первого порядка (Э1). Такой поток является потоком Пальма, поскольку величины 1,2,...,, получаются суммированием независимых интервалов. Вообще, потоком Эрланга k-го порядка Эkназывается поток, получаемый из простейшего, если сохранить каждую k1)-ую точку, а остальные выбросить. Найдем закон распределения промежутка времени τ между соседними событиями в потоке Эрланга k-го порядка (Эk ). Рассмотрим на оси Ot простейший поток с интервалами 1,2,... Величина τ представляет собой сумму k1независимых СВ 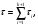 где 1,2,...,k1- независимые СВ с экспоненциальным распределением. Обозначим wkПРВ величины τ для потока (Эk ). Произведение wkdесть вероятность того, что величина τ примет значение между τ и τ+∆τ. Следовательно, последняя точка промежутка τ должна попасть на элементарный участок (τ и τ+∆τ), а предыдущие k точек простейшего потока – на участок (0, τ). Вероятность первого события равна P1∆∆; вероятность второго события 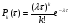 . Перемножая эти вероятности, получим . Перемножая эти вероятности, получим 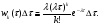 При ∆τ→ 0 находим точное равенство для ПРВ интервалов времени для потока Эрланга k-го порядка
Заметим, что математическое ожидание 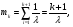 а дисперсия интервалов между событиями в потоке Эрланга Dkk12. Интенсивность Λk потока Эрланга k-го порядка а дисперсия интервалов между событиями в потоке Эрланга Dkk12. Интенсивность Λk потока Эрланга k-го порядка 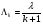 . Таким образом, при увеличении порядка увеличиваются математическое ожидание и дисперсия промежутка времени между событиями, а интенсивность потока падает. . Таким образом, при увеличении порядка увеличиваются математическое ожидание и дисперсия промежутка времени между событиями, а интенсивность потока падает. Рассмотрим, как будут изменяться характеристики потока Эрланга при увеличении k, если его интенсивность будет сохраняться постоянной. Пронормируем величину τ так, чтобы ее математическое ожидание (и, следовательно, интенсивность потока) оставались неизменными. Для этого изменим масштаб по оси времени и вместо τ рассмотрим величину 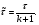 Назовем такой поток нормированным потоком Эрланга k-го порядка. ПРВ интервала 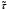 между событиями между событиями 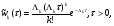 гдеkk1. Математическое 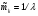 величины величины 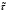 , распределенной по закону , распределенной по закону 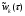 , не зависит от k. Дисперсия интервала , не зависит от k. Дисперсия интервала 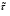 между событиями между событиями 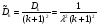 неограниченно убывает с возрастанием k. Это означает, что при неограниченном увеличении k нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными 1/λ. Это свойство потоков Эрланга дает возможность, задаваясь различными k, получать любую степень последействия: от полного отсутствия (k0 ) до жесткой функциональной связи между моментами появления событий (k =∞). неограниченно убывает с возрастанием k. Это означает, что при неограниченном увеличении k нормированный поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными 1/λ. Это свойство потоков Эрланга дает возможность, задаваясь различными k, получать любую степень последействия: от полного отсутствия (k0 ) до жесткой функциональной связи между моментами появления событий (k =∞).5.1.4. Нормальный поток событий Поток Пальма, для которого интервалы времени τ распределены по нормальному закону 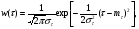 называется нормальным потоком [21]. Следует заметить, что понятие нормального потока можно рассматривать только как приближенное. Дело в том, что при нормальном законе распределения СВ изменяется в интервале (−∞,+∞) а интервал между событиями - положительная СВ, изменяющаяся в интервале (0, ∞). Однако интервал практически возможных значений СВ, распределенной по нормальному закону, равен (m3,m3). Таким образом, при условии m3можно сказать, что вероятность отрицательных значений СВ практически равна нулю, так как она меньше 0,003 (правило «трех сигм»). Именно для этого можно использовать нормальный закон распределения. В пределе, при 0, нормальный закон распределения переходит в регулярный. Рассмотрим связь потока Эрланга с нормальным потоком. ПРВ СВ τ, равной интервалу между заявками в потоке Эрланга, определяется по формуле (5.5). Функция распределения получается интегрированием 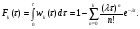 Для функции 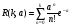 составлены специальные таблицы. При больших значениях параметра a (a20) для вычисления Rk,aможно использовать таблицы значений нормальной функции распределения: 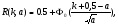 , где 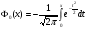 - интегралвероятностей. - интегралвероятностей. 5.2. Самоподобные (фрактальные) модели случайных потоков Рассмотренные пуассоновские модели потоков, когда ПРВ имеет показательный вид и входной поток обладает свойством марковости (см. главу 3), оказываются неадекватными при анализе трафика в сетях пакетной коммутации таких как Ethernet, Internet, Telnet и др. В подобных сетях обнаруживается долгосрочная зависимость или самоподобие. На интуитивном уровне это означает, что число событий на заданном временном интервале может зависеть от числа событий, поступивших в весьма отдаленные от него интервалы времени. При этом часто процесс носит «пачечный» характер. Проведенные в последние годы исследования показали, что поведение потока данных в таких сетях связи хорошо описывается с помощью моделей, основанных на теории фракталов. |