Методологические основы моделирования
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
Теорема 5. Упорядоченная пара (а,в) является парой связности для вершин u и v графа G тогда и только тогда, когда существует а вершинно- непересекающихся (u-v) путей, и в реберно- непересекающихся (u-v) путей не имеющих общих ребер с а предыдущими путями и, кроме того, наибольшие возможные числа таких путей равны именно а и в. На графе рис.27. между вершинами S и t существуют, как было показано ранее, 5 реберно – независимых путей: 1st = < e1, e8 ,e19> 2st = < e3, e10 ,e23> 3st = < e5, e14> 4st = < e2, e9 ,e15, e17 ,e21> 5st = < e4, e11 ,e22, e18 > При этом, первые три пути являются и вершинно- независимыми, проходящими через вершины {v5, v6, v7 }, которые составляют минимальное сечение по вершинам, т.е. определяют вершинную связность графа æ(G). Это означает, что в данном случае λ(G)=5, æ(G) =3 и упорядоченные пары (0, λ), (æ, 0) являются парами связностей для вершин S и t (v1и v11). Построим функцую связности для вершин s и t :
0 1 2 3 Рис.29. Функция связности σ (s,t) Координаты функции связности для вершин (s,t) показывают, сколько вершин и ребер нужно изъять, чтобы нарушить связность между этими вершинами. Всего таких пар æ + 1, в нашем примере их 4. Так, из рис.1.28. видно, что при сохранившихся вершинах {v5, v6, v7}, необходимо нарушить все ist путей (i=1,5). При удалении одной из трех вершин, необходимо нарушить 4 пути, при удалении 2 вершин –3 пути, а при удалении всех 3х вершин автоматически нарушается все 5 реберно – независимых путей. Теорема 6: В каждом графе наибольшее число реберно- непересекающихся реберных разрезов, разделяющих две вершины u и v, равно наименьшему числу ребер простого пути, соединяющего u и v, т.е. равно расстоянию (выраженному через минимальное число ребер) между этими вершинами, т.е. d(u,v). Например на графе рис.28 наибольшее число реберно- непересекающихся разрезов между вершинами S(v1 ) и t(v11) равно 2,т.к минимальный путь (цепь), состоит из 2х ребер е5 и е14 (3st = Такими сечениями являются: S1= < e1 ,e2 ,e3 ,e4 ,e5> и S2= < e14 ,e19 ,e21 ,e22 ,e23> Все остальные сечения будут содержать одно из ребер е5 или е14 . Способы перечисления путей и сечений изложены ранее. И так имея набор всех путей между произвольными вершинами, не представляет особого труда отобрать из них вершинно- и реберно- пересекающиеся и провести структурный анализ как глобальной, так и локальной связности. Проще всего анализ начать с выявления мостов и точек сочленения. Выявление точек сочленения и мостов производится по одному алгоритму: 1.i=1, n (для мостов j=1, m). 2.Удалить вершину vi (ребро еj). 3.Проверить связность графа. 4.Если нет, то vi (еj) точка сочленения (мост) выполнить 5, иначе выполнить пункт 6. 5.Подсчитать точки сочленения (мосты). 6.Восстановить вершину vi (ребро еj). 7.Вывод результатов. Простейший способ устранения точек сочленения и мостов заключает в том, что в компонентах связности G1 и G2 графа G, полученных после удаления точки сочленения (моста), определяют вершины dimin(G1) и dimin(G2) и соединяют их ребром. Поскольку в алгоритме поиска точек сочленения (мостов) встречается процедура проверки связности, то необходимо выбрать алгоритм проверки связности, работающий наиболее эффективно. Кроме того этот алгоритм будет встречаться и при изучении других вопросов, поэтому остановимся на нем несколько подробнее. Одним из наиболее экономичных (быстрых) алгоритмов определения связности является алгоритм Уоршелла. Алгоритм Уоршелла (Warshall) предназначен для определения связности графов. Он преобразует матрицу смежности А(ij) в матрицу наличия прямых или транзитных путей соответствующим переписыванием матрицы А(ij), поэтому говорят, что алгоритм работает “на месте”. Каждая вершина обрабатывается один раз, поэтому задача решается за один проход. Достоинством алгоритма является достаточно высокая скорость работы, недостатком - отсутствие контроля числа транзитов в пути, если для этого не принять специальных мер. Число транзитов может измениться от 0 до n-1. Результирующая матрица показывает, есть ли путь между произвольными вершинами исходного графа. Суть алгоритма Уоршелла заключается в следующем. Задается исходный граф G, размерностью nxn. Алгоритм строит последовательность таких графов, что Gi≤ Gi+1 , т.е. граф Gi является подграфом Gi+1 , а исходный граф G = G0 , 0≤ i ≤ n-1. Граф Gi (i ≥ 1) получается из графа Gi-1 после обработки вершины i в графе Gi-1. Обработка вершины i в графе Gi-1 включает добавление новых ребер в Gi-1 следующим образом. Пусть в графе Gi-1 присутствуют ребра Таким образом, описание алгоритма можно представлять следующим образом. 1.Ввести матрицу смежности графа A(i, j) 2.Положить i =1 до n 3.Положить j =1 до n 4.Если элемент матрицы смежности a( i, j ) равен нулю то перейти к 8 5.Положить k =1 до n 6.a( j, k ) = a( j, k ) or a( i, k ) 7.Положить k = k+1, если k <= n, то перейти к 5 8.Положить j = j+1, если j<= n, то прейти к 3 9.Положить i = i+1, если i<= n то перейти к 2 10.Результирующую матрицу проверить на полную связность. Работу алгоритма Уоршелла рассмотрим на примере: G0 G1 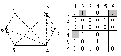 i=1 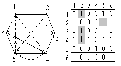 G1 G2 G1 G2i=2 G2 G3 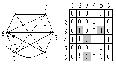 i=3 <6, 2><6,5> G3 G4 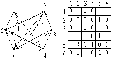 i=4 i=4 < 4, 5 >;< 4, 6 > < 5, 4 >; < 5, 6 > G4G5 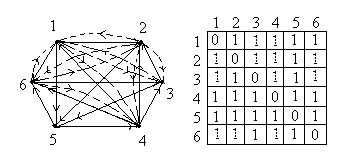 i=5 < 5, 4 >;< 5, 6 > < 4, 5 >;< 6, 5 > < 1, 6 > ;< 2, 1> ;<2,3>; <2,4>;<2,5>;< 2, 6>;<3,1>;<3,2>;<3,4>;<3,5>;<3,6>; <6,1>;<6,2>; <6,3>; <6,4>;<6,5> 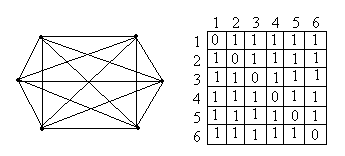 G5G6 При i = 5 получен полносвязный ориентированный граф, эквивалентныйнеориентированному. Ребра Ребра Ребра Добавляемые ребра На этом работа алгоритма заканчивается. Лекция 11 СИНТЕЗ СЕТЕЙ С МАКСИМАЛЬНОЙ СВЯЗНОСТЬЮ 1. Степенная последовательность вершин графа При синтезе сетей связи с заданными свойствами важное значение имеют показатели степеней вершин. Степенной последовательностью называют список степеней вершин графа. Чаще всего этот список задают в виде упорядоченного (вариационного ) ряда по мере убывания или возрастания степеней. Свойства графов связаны со свойствами степенных последовательностей как минимум на уровне необходимых условий. Так, чтобы графы были изоморфными, необходимым условиям является равенство степенных рядов, чтобы граф был максимально связен, необходимо равенство степеней или максимум однородности степеней и т.д. таким образом, свойства степенных последовательностей во многом определяют свойства графов, и по заданным степенным последовательностям иногда удается синтезировать графы с заданными свойствами. Прежде всего возникает вопрос- по всякой ли конечной последовательности целых чисел d1, d2,…,dn можно построить граф. Последовательность целых чисел называют графической, если можно построить такой граф, чтобы члены последовательности были степенями вершин. Чтобы последовательность была графической, она должна быть сжимаемой. Степенную последовательность называют правильной если выполняются два условия: n-1≥ d1≥d2….≥dn; 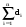 - четное число. - четное число.Проверку последовательности на сжимаемость проведем вместе с алгоритмом построения графа на примере. Пусть задана последовательность чисел, удовлетворяющая условию k1≥ k1≥….≥kn П1=5 ; 4; 3; 3; 2; 1. Последовательность сжимается путем выполнения следующих операций: из k1 вычитается k1 ; из k2; k3; k3;…; kk+1; вычитается 1 полагается k1 = 0; из оставшихся чисел формируется новая последовательность k1 ≥ k2 ≥….≥ kn; сжатие производится до тех пор, пока все числа не станут равными нулю, или появятся отрицательные. k1; k2; k3; k4 ; k5; k6 k1; k2; k3; k4 k2; k3 5; 4; 3; 3; 2; 1 3; 2; 2; 1 1; 1 3; 2; 2; 1; 0 1; 1; 0 0 v1; v2; v3; v4; v5; v6 v2; v3; v4 v3; v4 Последовательность сжимаемая, значит графическая, граф состоит из 6 вершин со степенями кi = di . Первый шаг сжатия последовательности является первым шагом построения графа, т.е. из вершины k1 проводятся k1=5ребер в вершины v2; v3; v4; v5; v6.(Ребра показаны сплошными линиями). Второй шаг сжатия последовательности является вторым шагом построения графа. Из вершины v2 с k1 =3 проводятся 3 ребра в вершины v3; v4; v5.(Ребра показаны пунктирными линиями). Третий шаг –из вершины v3 проводятся ребро в v4 граф со степенным рядом вершин d:{5;4;3;3;2;1} построен.(ребро V3V4 показана штрих-пунктирной).  Рис. 1. Граф G1 (П1) Пусть теперь последовательность имеет вид: П2 = 5; 4; 4; 3; 2; 2 Первый шаг – ведущая вершина v1(5) соединяется с вершинами v2; v3; v4; v5; v6, степенная последовательность принимает вид : 0 3 3 2 1 1 Второй шаг- ведущая вершина v2(3) соединяется с вершинами v3; v4; v5, сжимаемая последовательность принимает вид: 0 0 2 1 0 1. Третий шаг- ведущая вершина v3 соединяется с вершинами v4; v6 , конец.  Рис. 2. Граф G2(П2) Для последовательностей П1, П2 выполняется одно из необходимых условий изоморфного вхождения графа G1(П1) в граф G2(П2), а именно П2≥ П1, т.е. 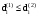 . В данном случае этого условия достаточно, чтобы граф G1 вкладывался в граф G2. Графы будут изоморфны, если удалить ребро v3v6, в этом случае совпадут и последовательности П1 и П2. Однако в общем случае этого условия не достаточно. . В данном случае этого условия достаточно, чтобы граф G1 вкладывался в граф G2. Графы будут изоморфны, если удалить ребро v3v6, в этом случае совпадут и последовательности П1 и П2. Однако в общем случае этого условия не достаточно.Изложенный способ построения графа по заданной степенной последовательности называют ℓ- процедурой, а вершину k1 на каждом шаге- ведущей вершиной. 2. Алгоритм синтеза графов с максимальной связностью В зависимости от выбора ведущей вершины ℓ- процедура может строить различные реализации графов, в том числе и с заданными свойствами. Так с помощью ℓ- процедуры можно построить такую реализацию графа, у которой реберная связность (G) будет максимальной. Основанием для этого служит теорема Д. Уэла: каждая правильная графическая степенная последовательность имеет реализацию, число реберной связности которой (G)=dn. Такая реализация строится ℓ- процедурой, на каждом шаге которой ведущей является вершина с минимальной степенью. Пример. Задана последовательность: П3= 5 4 4 3 2 2. Построить граф с максимальной реберной связностью 1шаг- ведущая вершина v6(2) соединяется с v1 и v3, последовательность принимает вид: 4 3 4 3 2 0; 2шаг- ведущая вершина v5(2) соединяется с вершинами v1,v3, последовательность принимает вид: 3 3 3 3 0 0; 3-ий шаг- ведущая вершина v1(3) соединяется с вершинами v2, v3 и v4, последовательность принимает вид : 0 2 2 0 0; 4-ый шаг- ведущая вершина v2(2) соединяется с v3, v4, последовательность принимает вид 0 0 1 1 0 0; 5-ый шаг- соединяются вершины v3 и v4, конец. 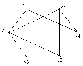 Рис.3. Граф G3(П3). Полученный граф G3(П3) изоморфен графу G2(П2) . Изоморфность доказывается равенством последовательностей П2 = П3( необходимое условие) и наличием гамильтоновых циклов: С2 = v1 v6 v3 v4 v2 v5 v1 C3 = v1 v5 v3 v4 v2 v6 v1 , которые совпадают при подстановке v5→v6 и наоборот, т.е. при перенумерации вершин v5 и v6 любого из графов (достаточное условие). 3. Алгоритмы синтеза графов с максимальной связностью при заданном числе вершин и ребер. Рассмотрены случаи построения графов, в том числе и с максимальной реберной связностью, когда заданы степенные последовательности вершин. Однако чаще задача формализуется другим образом. Задано: n – число вершин графа и m –число ребер, которые нужно распределить на вершинах графа таким образом, чтобы граф обладал наибольшей реберной связностью. Харари показал, а Свами привел подробную процедуру построения графа Hk,n, который является k-связным и содержит ровно m=[kn/2] ребер. Процедура заключается в том, что в графе Hk,n между i-й и j-ой вершинами ребра прокладываются по следующим правилам: I-случай k=2r-четно: тогда H2r,n строится на вершинах v0,v1,…,vn-1 и две вершины vi и vjсмежны, если i-r ≤ j ≤ i+r . II-случай k =2r+1: n- четно: тогда H2r+1,n получается из графа H2r,n введением ребер, соединяющих вершины vi и vjдля i=0,1,2,…,n/2 и j=i+n/2(modn). III-случай k=2r+1: n-нечетно, тогда H2r+1,n получается из графа H2r,n введением ребер, соединяющих вершины vi и vjдля i=0,1,2,…,(n-1)/2 и j=i+(n+1).2(mod n). Блок –схема алгоритма, реализующего процедуру Свами-Хараи приведена на рис.4. Процедура работает при соблюдении равенства m=[k.n/2] с учетом выполнения требования 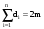 . В этом ограничение процедуры. . В этом ограничение процедуры.При произвольном m и n и естественном ограничении 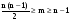 хорошо работает алгоритм Колесникова-Федорова. хорошо работает алгоритм Колесникова-Федорова.Суть его заключается в следующем. Для синтеза оптимальной структуры ее граф строят путем набора различных последовательных структур в виде независимых остовных деревьев или поддеревьев. При этом каждая новая последовательная структура для повышения равномерности распределения значений степеней вершин должна начинаться с другой вершины и порядок чередования вершин следует менять. Элементы матрицы смежности, отображающие эти последовательные структуры, размещаются параллельно главной диагонали, состоят из одной или двух поддиагоналей и содержат n-1 или менее элементов. Метод работает при любом соотношении m и n. Тонким моментом алгоритма является выбор вершины перехода на очередную диагональ, поскольку его иногда не удается формализовать, но реализовать эвристически просто из-за наглядности “ручной” реализации. 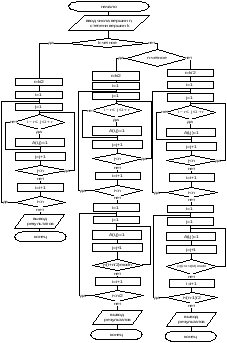 Оба алгоритма дают одинаковые результаты, когда k = 2m/n – целое число. Для исключения эвристических решений, когда k = 2m/n – не целое число, метод может быть усовершенствован и существенно упрощен путем переноса процесса оптимизации из области формирования последовательных структур в область формирования оптимальных (рациональных) степенных последовательностей вершин синтезируемого графа. Оба алгоритма дают одинаковые результаты, когда k = 2m/n – целое число. Для исключения эвристических решений, когда k = 2m/n – не целое число, метод может быть усовершенствован и существенно упрощен путем переноса процесса оптимизации из области формирования последовательных структур в область формирования оптимальных (рациональных) степенных последовательностей вершин синтезируемого графа.Рис.4. Блок-схема алгоритма, реализующего процедуру Свами-Харари. При этом требование максимальной равномерности степеней вершин и равномерного распределения оставшихся ребер удовлетворяется следующим образом. Определяется минимальная степень вершин dimin=[2m/n] в остатке получается 1≤ r ≤ n-1 вершин, это значит, что n-r вершин имеют степень dimin, а r- вершин имеют степень dimах= dimin+1. Причем порядок распределения вершин с разными степенями должен быть также максимально равномерным. При этом , если r Естественно, что количество оставшихся вершин должно быть четным (каждое ребро содержит 2 вершины), а получаемая последовательность - графической. Далее по полученной степенной последовательности строится граф максимальной связности с использованием ℓ-процедуры [1 ]. Пример. Дано n=4, m=5 построить граф максимальной связности. Решение Определим k= dimin = (2m /n)+r = 2.5/4 =2+2(mod4). dimax = dimin +1=3 Определим степенную последовательность- это П1= {2;3;2;3} или П2 = {3;2;3;2}. С помощью ℓ-процедуры строим граф по П1: 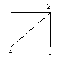 2 3 2 3 1. Соединяем 1 со 2-ой и 4-ой вершин 0 2 2 2 2. Соединяем 2-ой со 3-й и 4-й вершин 0 0 1 1 3. Соединяем 3-ю и 4-ю вершин 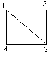 Построим граф по П2: Построим граф по П2:3 2 3 2 1. Соединяем 2-ю с 1-й и 3-й вершин 2 0 2 2 2. Соединяем 1-ой с 3-й и 4-й вершин 0 0 1 1 3. Соединяем 3-ю и 4-ю вершин Графы изоморфны, граф G2(П2) получается из графа G1(П1) поворотом на 90 ο против часовой стрелки вокруг центра симметрии с помощью подстановки 1 2 3 4 t = 4 1 2 3 Как и следовало ожидать, оба графа имеют максимальное ( при заданных m и n ) число остовных деревьев- 8. |
