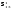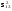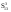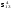Методологические основы моделирования
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
Напомним, что матрицей смежности А=||aij|| помеченного графа G(V,E) с n вершинами называется (nxn)- матрица, в которой аij =1 , если вершина viсмежна с вершиной vj и аij=0 в противном случае. Если граф не является связным, то путем соответствующей нумерации вершин матрицу смежности можно представить блочной матрицей диагонального вида, в которой каждый блок соответствует одной из компонент связности, например: 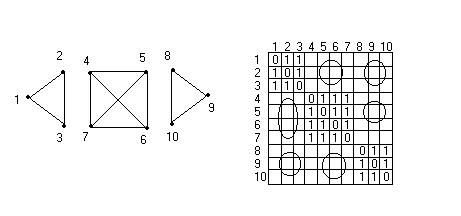 Рис.20. Граф с тремя компонентами и его блочная матрица смежности Поскольку компоненты и в матрице смежности не имеют общих элементов, то каждую из них можно рассматривать отдельно. С помощью матриц смежности, используя различные алгебры, можно определить наличие путей различной длины между произвольными вершинами, количество таких путей и перечисление таких путей. Если использовать булеву алгебру, то элемент anij показывает, есть ли между вершинами vi и vj путь, длиной меньше или равной n ребер. При этом о значении диагональных элементов матрицы договариваются заранее исходя из сущности решаемой задачи
Графы G1 и G2, соответствующие матрицам смежности А1 и А2 приведены на рис.21; 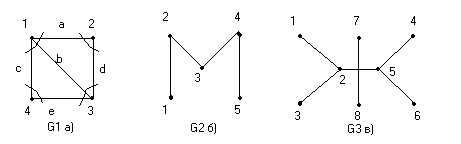 Рис.21. Графы G1 , G2 и G3 Граф G1 после возведения его матрицы смежности А1 в квадрат становиться полносявзным, т.е. каждая его вершина связана со всеми остальными либо одним ребром в соответствии с матрицей А1 , либо путем, состоящим из двух ребер в соответствии с матрицей А21 . Появляющиеся петли при вершинах, соответствующие диагональным элементам , можно принимать или не принимать во внимание, в зависимости от решаемой задачи. При возведении матрицы А2 в квадрат в графе G2 появляются дополнительные связи между вершинами v1 иv3 (v3 и v1), v2 и v4 (v4и v2 ), v3 и v5 ( v5 и v3) и граф G2 принимает вид, как показано на рис.22; 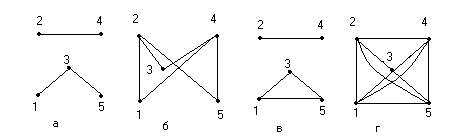 А) 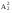 ; б) ; б) 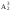 ; в) ; в)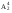 ; г) ; г) 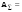 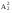 U U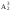 U U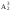 Рис.22.Механизм появления новых связей при возведении в степень {2,3,4}матрицы А2. При возведении матрицы А32 = А22 х А1 появляются новые пути из тех ребер, связывающие вершины v1 иv2 ; v1 иv4 и.т.д произведя сложение матриц по правилам булевой алгебры, получим : АΣ = А2U А22U А32U А42 0 1 1 1 1 1 0 1 1 1 АΣ = 1 1 0 1 1 1 1 1 0 1 1 1 1 1 0 Граф, соответствующий этой матрице, без учета петель является полносвязным и показан на рис.22. В матрицах А2 со степенью меньше 4 элементы а15 = а51 = 0. Поэтому m = 4 является минимальной степенью, при возведении в которую элементы матрицы Аm содержат только положительные элементы. В этом случае все вершины являются достижимыми из любой вершины путем, состоящим из не более чем m ребер (дуг) . Граф G и соответствующая ему матрица смежности А называются примитивными, а m – индексом примитивности. На рис.21 в граф G3 не является примитивным, поскольку из его вершин 7 и 8 нет ребер , связывающих их с другими вершинами. Для определения количества путей различной длины применяют возведение в степень матрицы смежности по правилам обычной алгебры . Так, при возведении в квадрат матрицы А1, соответствующей графу G1 на рис.21а получим :
На главной диагонали стоят степени вершин . Из вершины v1 в v2 есть один путь из двух ребер е2 е4 ; в вершину v3 – два пути е1 е4 и е3 е5; в вершину v4- е2 е5 . Эти пути можно определить только визуально из графа, по матрице же можно определить только их количество. Для перечисления путей применяют так называемые структурные матрицы и одну из равновидностей булевой алгебры. Структурная матрица в определяется таким образом: bij, если вершины vi и vj соединены ребрам и i < j В = 1, если i = j bij, если вершины vi и vj соединены ребром, но i>j 0 в остальных случаях алгебра такова: 1 U 1 = 1 ; 1.0 = 0.1=0 ; 1 U 0 = 0 U 1=1 ā .а=0 ; а U а = а ;а Uав = а ; 1 U а =1 для графа G1 рис 31а структурная матрица примет вид :
Для удобства заполнения матрицы В2 записываем i-ю строку, под ней j-й столбец и производим умножение строки на столбец по изложенным правилам. 1 а в с В211= 1 ā 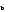 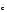 = 1*1U а* ā U в* = 1*1U а* ā U в*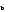 Uс * Uс *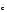 = 1 = 1 1 а в с В212= а 1 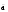 0= 1*aU а 1U в 0= 1*aU а 1U в 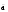 U с 0 = aUв U с 0 = aUв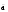 1 а в с В213= в d 1 ē = 1*вU а dU в Uс ē = вUаdU с ē 1 а в с В214= с 0 е 1 = сU а 0UвеU с = сUве Для того, чтобы перечислить одно, двух и трехзвенные пути, необходимо умножить матрицу В2хВ1 т.е. В3= В2хВ. Получим, например, первую стоку матрицы В3
= 1U ā b 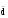 U a U a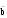 d UbceUcb ē = 1 d UbceUcb ē = 1
=a U a b 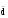 U b U b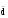 U U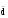 c ē = a U b c ē = a U b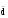 U c ē U c ē 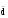
= b U ad U b U ad U c ē U c ē = b U ad U c ē
= c UbeUade
= ā b U d U ā 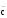 e e
= ā U c 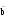 d U de U ā be d U de U ā be
= 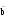 c Uc ā c Uc ā 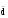 U e U U e U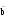 c cматрица В3 имеет вид:
Дальнейшее возведение в степень матрицы смежности не дает новых путей (только циклы), а алгоритм определения базисных циклов был рассмотрен ранее. В каждой из клеток (n-1) степени структурной матрицы представлены все пути, ведущие из вершины vi в вершину vj. Каждую из клеток в связи с этим можно представить отдельной матрицей путей Мst строкам которой соответствуют пути, а столбцам –дуги, входящие в эти пути. Например, для клетки 13 матрица путей примет вид:
k13 = 113U213U313 = b U ad U c ē . Перечисление путей Мst из произвольной вершины s в произвольную вершину t может быть получено из структурной матрицы В раскрытием определителя подматрицы Вts, получаемого из структурной матрицы В вычергиванием s-го столбца и t –й строки: Мst = detвts = | вts | 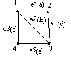 1 a b c a b c 1 a b c a b cв= a 1 d o ;в13= 1 d o b d 1 e o e 1 c o e 1 a b c k13=|в13| = 1 d O =а d OU b c UO = ad U b Ucе o e 1 e 1 e 1 Для вершин v1 и v3 таких независимых путей 3 – это b(e2) Uad(e1e4) Uce(e3e5), для вершин v2 и v3 таких пути два :d(e4) U a b (e1e2). Это является следствием того, что степень вершины d(V4) = 2 , поэтому и число независимых путей в нее и из нее не может превышать этого числа. И вообще число независимых путей из одной вершины в другую не может превышать минимальную степень одной из них. В наших примерах : d(v1) = 3; d(v2) = 2; d(v3) = 3; поэтому между v1 и v3 может быть не более трех независимых путей, а между v2 и v3 не более двух . В множестве путей М23 пути ab и асе содержат общее ребро а, поэтому они не могут быть независимыми. Множество путей между двумя произвольными вершинами связано с понятием “сечение”, которое является более общим случаем понятия “разрез”. Напомним, что разрез – это минимальное число ребер, удаление которых разбивает граф на два связанных подграфа. Сечением называется минимальное число ребер или вершин, удаление которых делает две вершины графа vs и vt несвязными. Для того, чтобы сделать две вершины vs и vtнесвязными, нужно либо нарушить все пути Мst, связывающие эти вершины, либо хотя бы одно из сечений st ε Sst , где Sst – множество сечений между вершинами vs и vt. Между множеством путей Мst и множеством сечений Sst , а также множеством базисных разрезов существуют однозначные взаимосвязи. Множество сечений Sst можно получить из дизъюнктивно-нормальной формы записи множества путей Мst , заменив знаки конъюнкции на знаки дизъюнкции и наоборот, используя булеву алгебру. Поскольку в булевой алгебре 1 U 1 = 1, то а.а = а; а U а = а; 1.а = а; 1 U а = 1; а(а U в) = а; а Uав = а; а. ā = 0; а U ā =1. Например, М13 = b U ad Uce → S13 = b.(a U d).(c U e). Здесь U и (.) –знаки дизъюнкции и конъюнкции. Скобки удобнее раскрывать последовательно. b(a U d) = (b a U b d) ( b a U b d )( cU e ) = a b c U b c d U a b e U b d e = S13 Аналогично из перечисления сечений Sst можно получить выражение для перечисления множества путей Мst, произведя замену знаков дизъюнкций и конъюнкций. S13 =a b c U b c d U a b e U b d e → М13 = ( a U b U c).(b U c U d).(a U b U c ).(b U d U c).(a U b U c).(b U c U d)= abUadUacU b UcbUcdU c = (adU b U c) посколку a Uab = a такие пары скобок дает: (a U b U e)(b U d U e) = abUadUacU b UbdUbcUacUbcU e = adU b U e окончательно получим: (adU b U c)(adU b U e) = ad UabdUabeUabdU b U be U cad Uce = b U ad Uce = М13 .Запишем полученное множество сечений 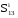 в форме матрицы : в форме матрицы :
Запишем также матрицу базисных разрезов относительно остовного дерева{e1 , e2 , e3}, полученную ранее
Из соотношения матриц сечений и базисных разрезов видно, что: S113 = S1 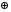 S2 S2 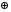 S3 = S4 S3 = S4S213 = S2 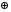 S3 = S5 S3 = S5S313 = S1 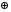 S2 = S6 S2 = S6S413 = S2 = S2 Таким образом, каждое сечение является линейнной комбинацией базисных разрезов. Запишем полученные разрезы в одну матрицу.
Как видно из графа G1 на рис.21а, матрица охватывает все возможные разрезы этого графа. Множество сечений Sst является подмножеством всех возможных сечений. Таким образом, нами рассмотрены способы определения по матрице смежности или структурной матрице наличия путей, их количества и перечисления путей между произвольными вершинами графа. На основе логическной формы записи множества путей рассмотрен способ получения сечений и установлена взаимосвязь между множеством сечений и базисным множеством разрезов. Как видно из графа G1 на рис.1.21а, матрица охватывает все возможные разрезы этого графа. Множество сечений Sst является подмножеством всех возможных сечений. Таким образом, нами рассмотрены способы определения по матрице смежности или структурной матрице наличия путей, их количества и перечисления путей между произвольными вершинами графа. 2. Связность Это свойство графов является ключевым при исследовании сетей связи и прежде всего при оценках устойчивости сетей ( систем ) связи и определении качества связи. Применительно к сетям связи связность характеризуется наличием каналов связи между заданными узлами, их количеством и качественными характеристиками, способностью обеспечивать передачу заданных потоков сообщений с заданными требованиями к качеству связи в условиях различных воздействий противника на узлы и каналы связи. Для исследования различных характеристик сети на графах вводится неструктурная информация в виде весовых коэффициентов, но и изучение только структурных свойств графов, характеризующих, их связность имеет существенное значение. Весь предыдущий материал по теории графов является минимальной необходимой базой для исследования сетей связи, анализа заданных сетей и синтеза сетей с заданными свойствами. Напомним, что граф называется связным, если из любой вершины vi в любую другую вершину vj существует путь( маршрут). При этом некоторые вершины и ребра могут быть особенными. Так, вершина, удаление которой увеличивает число компонент графа называется точкой сочленения. Ребро с аналогичным свойством называется мостом. Неразделимым называется связный, непустой не имеющий точек сочленения граф. Блок графа- это его максимальный неразделимый подграф. Полносвязный блок называют кликой. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

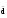 Ua
Ua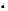
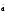
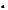
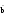 d
d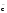
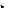 d
d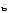 c
c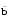 d
d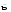 U ā c ē
U ā c ē