Методологические основы моделирования
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
|
Раздел 2. МОДЕЛИ И МЕТОДЫ ИССЛЕДОВАНИЯ СТРУКТУРНЫХ СВОЙСТВ СЕТЕЙ СВЯЗИ ОРИЕНТИРОВАННЫЕ И НЕОРИЕНТИРОВАННЫЕ ВЗВЕШЕННЫЕ ГРАФЫ, ИХ ВИДЫ, СВОЙСТВА И МЕТОДЫ ФОРМАЛЬНОГО ОПИСАНИЯ. 1. Виды и свойства графов. Граф – множество V (vertex) вершин и набор E (edge) пар вершин-множество ребер. Пары могут быть упорядоченными и неупорядоченными. Граф обозначается через G(V , E). Неупорядоченная пара вершин называется ребром, упорядоченная – дугой. Граф, содержащий только ребра называется неориентированным, содержащий только дуги – ориентированным, содержащий и ребра и дуги – смешанным. Дуга или ребро могут начинаться и заканчиваться в одной вершине. Такая дуга (ребро) называется петлей. Некоторые вершины могут соединяться более чем одним ребром, или дугой одного направления. В этом случае они называются кратными. Иногда рассматривают только графы, не содержащие петель и кратных ребер. Граф, не содержащий петель, но допускающий кратные ребра, называют мультиграфом, а граф содержащий петли и кратные ребра, называют псевдографом графом. Графы без петель и кратных ребер называют обыкновенными. В дальнейшем мы эти понятия различать не будем, если это не вызывает недоразумений. Обычно граф представляется диаграммой, которую и называют графом, т.е. графическим изображением введенного понятия G (V, E) , где: V- множество вершин; E – множество ребер. G1( V , E ) G2 ( V , E ) Рис.1. Помеченный G1 и непомеченный G2 смешанные графы. Вершины, соединенные ребром или дугой называют смежными. Ребро (дуга) и любая из его вершин называются инцидентными. Если два различных ребра инцидентны одной и той же вершине, то они называются смежными. Например, вершины v1v2 , v2v3 ,v1v4смежны, вершина v3 инцидентна ребру e4 и дуге е5 , а ребра е1 и е2, инцидентные вершине v2 – смежны. Граф называется помеченным (или перенумерованным), если его вершины отличаются одна от другой какими либо пометками, например v1,v2,…,v6. Так, на рис.1. граф G1 (V , E) – помеченный граф, а граф G2(V , E) - нет. В теории графов граф рассматривается как некоторый комбинаторный объект, в котором не учитываются такие свойства конкретных графов, как природа вершин и ребер, их относительное расположение, кривизна линий, размеры графа ит.д. Метки вводятся лишь для того, чтобы можно было математически представить различные графы теми или иными способами. Один из способов представления, а именно графический, был рассмотрен ранее, рассмотрим другие способы. Матрицей смежности A=|| aij|| , соответствующей графу G (V, E) , называют матрицу, у которой элемент aij равен 1 (или числу ребер), если между вершиной viи vjсуществует ребро (или несколько) и aij =0 , если между вершинами vi и vj нет ребер. Пример графа G(V, E) и его матрицы смежности приведен на рис.2. А= Рис.2. Граф G(V, E) и соответствующая ему матрица смежности A=||aij|| Размерность матрицы смежности равна nn , где n=|V|, т.е. n равно числу элементов во множестве вершин V={vi}. В матрице инцидентности B=||bij|| граф G(V,E) ,bij=1,если вершина viявляется начальной для ребра ej, bij= -1 ,если вершина vi является конечной для ребра ej и bij=0 в противном случае, т.е. 1, если vi  V – начальная вершина для еi; V – начальная вершина для еi;Bij= -1, если vi  V – конечная вершина для еj; V – конечная вершина для еj;0 - в противном случае. 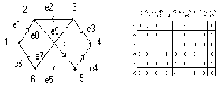 В = Рис.1.3. Граф G(V, E) и его матрица инцидентности. Иногда встречаются термины: “матрица смежностей”, “инцидентностей”, “инциденций”, которые употребляются несколько реже. Если граф неориентированный, то в матрице инцидентности элементы bij принимает значение '' 1 '' , если вершина vi и ребро ej инцидентны и '' 0 '' в противном случае. Пример: 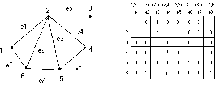 В = Рис.1.4.Неориентированный граф и его матрица инцидентности. Размерность матрицы инцидентности B[n х m] , где n=|V| - число элементов множества V={vi}, т.е. число вершин, m-число ребер. Здесь для ребер введены обозначения: e k= Для ориентированного ребра (дуги )ek это означает, что оно начинается в вершине i и заканчивается в вершине j . Для неориентированного ребра ek= В верхних частях таблиц инцидентности графов на рис 1.3 и 1.4 дуги и ребра графов ek заданы списками. Такие списки однозначно определяют граф. Форма представления графов списками ребер (дуг ) особенно удобна, когда размерность матрицы B[n x m ] велика, а число ребер ek мало. Граф на рис.1.3 задается списком ребер G(V,E):<1,2>;<2,1>;<3,4>;<4,5>;<5,6>;<6,1>;<6,3>;<1,4>;<2,5> граф на рис.1.4. задается также <1,2>;<2,6>; <2,5>; <2,4>; <2,3>; <4,5>; <6,5>; <1,6>. Матрица смежности A представляет из себя множество размерностью VV, каждый элемент которого aij может принимать значение 0 или 1 . Этим самым между элементом ai (из i-ой строки) и элементом aj (из j-го столбца) устанавливается бинарное отношение R (relation). Применительно к теории графов отношение ai R ajозначает, что вершина ai соединяется ребром с вершиной aj . Для неориентированных ребер отношение взаимно однозначно, для ориентированных только в том случае , если между вершинами есть дуги противоположной направленности . В связи с этим различают прямое и обратное отображение для каждой вершины. Это позволяет задать граф с помощью отображения R и R-1 где R- список вершин в которые отображается данная вершина , а R-1 список вершин, которые отображаются в данную вершину. Пусть задан граф G(X ,F) на рис.5 тогда: F(x1)={x2}:F-1(x1)={x5} F(x2)={x5}:F-1(x2)={x1,x3} 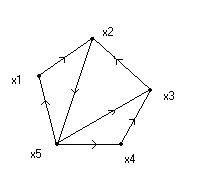 F(x3)={x2}:F-1(x3)={x4,x5} F(x4)={x3}:F-1(x4)={x5} F(x5)={x1,x3,x4}:F-1(x5)={x2} Рис.5. Способ задания обыкновенного ориентированного графа G(X, F) с помощью прямого и обратного отображения. Для неориентированных графов пользуются списком смежности. Рис.6. Способ задания неориентированного графа списком смежности. В списке смежности определяется сколько и какие вершины смежны данной вершине. Для неориентированного графа число ребер, инцидентных данной вершине называют степенью вершины Vi графа G и обозначают di, или d(vi). Если граф G (без петель ) имеет n вершин и m ребер, то вершина Vi называется изолированной, если di =0 и концевой или висячей, если di =1. Граф, у которого все вершины имеют одинаковые степени (равные k) называется регулярным степени k, или гомогенным.  А б в г Рис.7. Регулярные графы степени k=2,3,4,5 При k = n-1 регулярный граф становится полным, т.е. таким, у которого каждая вершина соединена со всеми другими равно одним ребром. Графы на рис. 7.а, б, в и г регулярные, со степени k=2,3,4 и 5. В ориентированном графе G для каждой вершины Vi определяется полу степень исхода и захода как количество дуг, исходящих из вершины Vi и заходящих в нее. Полустепени исхода и захода численно равны мощности множеств прямого и обратного отображений Viвершин. Так для графа на рис 5 |F(x1)|=1 ; |F-1(x1)|=1 ; |F(x2)|=1; |F-1(x2)|=2 ….,|F(x5)|=3 ; |F-1(x5)|=1. Часто для характеристики вершин ориентированных графов по аналогии с комплексными числами используют составную степень di , записываемую одним числом. Число разбивается на две половины, каждая из которых состоит из одной (для n 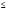 9), двух (n 9), двух (n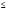 99), трех(n 99), трех(n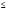 999) и.т.д позиций, где количество позиций определяется ближайшим большим целым числом к десятичному логарифму количества вершин (n) в графе. Например: 999) и.т.д позиций, где количество позиций определяется ближайшим большим целым числом к десятичному логарифму количества вершин (n) в графе. Например: d1=21 d2=04 d3=21 d4=11 d5=32 d6=21 Рис.1.8. Ориентированный граф и составные степени его вершин. Для графа с числом вершин 99 n 10 составная степень имеет вид aiakbjbe; где: ai, ak-десятки и единицы числа полустепени исхода,bj, be – десятки и единицы числа полустепени захода.Пусть d5 = 2236 . Это означает, что из 5-ой вершины исходит 22 дуги и заходит 36.d163 = 217613 означает , что из 163-й вершины исходит 217 дуг и заходит 613 ит.д. 2. Изоморфность графов Для графов, как и для других геометрических фигур, существует отношение эквивалентности. Если для геометрических фигур устанавливаются отношение равенства, подобия, конгруэнтности, то для графов аналогом таких отношений является понятие изоморфности (изоморфного вложения, наличие изоморфной части двух графов), отражающее степень совпадения структурных свойств двух графов. При этом геометрические размеры, формы представления не играют роли. Два графа G(X ,F) и H(Y, P) называются изоморфными, если существует взаимно однозначное соответствие между множествами вершин X , Y и множествами ребер F, P , сохраняющее отношение смежности (инцидентности). Другими словами , если вершинам xi , xj в графе G соответствуют вершины yk , ye в графе H, то ребро (дуга) в G(X , F), имеющие концевые вершины xiи xj , должно соответствовать ребру в H(Y , P) , имеющему концевые вершины yk, ye и наоборот . На рис.1.9. приведены два изоморфных графа G(X ,F) и H(Y , P) а)G (X , F ) б) H ( Y , P ) Рис.1.9.(а,б). Графы G , H – изоморфны. Оба графа имеют по 6 вершин , 9 ребер .Степени вершин у всех ребер одинаковы k = 3. Изоморфизм графов устанавливается подстановкой: t = x1 x2 x3 x4 x5 x6 y1 y4 y2 y5 y3 y6 Запишем оба графа в виде списков смежности:
и проверим справедливость подстановки для ребер. F(x1) это следует из подстановки: t = x1 , x2 , x6 y1 , y4,y6 ; F(x2) что следует из подстановки: t = x2 , x1, x3 , x5 y4 , y1,y2 , y3 Этих проверок достаточно, поскольку остальные строки в списке смежности идентичны, т.е. индексам 2,4,6 у вершин графа G(X, F) , соответствуют 4,5,6 у вершин графа H(V, P), а индексам 1,3,5 у вершин графа G , соответствуют индексы 1,2,3. Таким образом, графы G(X, F) и H(Y, P) изоморфны. Как видно из примера, необходимым условиям изоморфности является равенство числа вершин (n), ребер (m), степеней (полустепеней исхода и захода) вершин, которые ставятся в соответствие друг другу. Понятие изоморфности позволяет распространять некоторые очевидные свойства одного графа на другой. Так граф H(Y ,P) на рис.1.9 является двудольным , т.е. таким графом, множество вершин которого Y можно разбить на два непересекающихся подмножества Y' и Y'' (т.е. Y=Y'U Y'',Y' 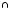 Y''= Y''= ) так , что каждое ребро соединяет некоторую вершину из Y' с некоторой вершиной Y''. ) так , что каждое ребро соединяет некоторую вершину из Y' с некоторой вершиной Y''.В рассматриваемом примере для графа H(Y, P) такими подмножествами являются Y'={y1,y2,y3}, Y''={y3,y4,y5} В графе G(X , F) им соответствуют подмножества: X'= { x1 ,x3, x5 }, и X'' ={ x2 ,x4, x6 } поэтому граф G(X, F) также является двудольным. Кроме того , графы G(X , F) и H(Y , P) являются полными двудольными поскольку каждая из вершин одного подмножества соединяется с каждой вершиной другого подмножества, что хорошо видно как из графического представления, так и из представления графов списками смежности. Под двудольным графом часто понимают граф, в котором заранее заданна определенное количество вершин V' и V'' (доли). Распространим теперь некоторые вполне очевидные свойства графа G(X,F) на граф H(Y,P). Автоморфизмом графа называют изоморфное отображение графа на себя. Граф G(X,F) на рис.9а обладает несколькими автоморфизмами . Например , если вращать граф по часовой стрелке , то циклические подстановки дают 6 изоморфных графов 1 2 3 4 5 6 2 3 4 5 6 1 3 4 5 6 1 2 4 5 6 1 2 3 5 6 1 2 3 4 6 1 2 3 4 5 1 2 3 4 5 6 Кроме этих преобразований циклического характера можно произвести вращение графа G(X,F) вокруг ребер 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 6 5 4 3 2 3 2 1 6 5 3 5 4 3 2 1 6 Как видно из подстановок для ребер, вокруг которых осуществляется поворот на 180 подстановки вершин являются тождественными т.е. у ребра <1,4> вершина 1 отображается в 1 , вершина 4 – в 4 и.т.д. Прежде чем рассмотреть автоморфизмы графа H(Y,P) введем понятия маршрута, цепи, цикла. Последовательность ребер Замкнутая (простая) цепь называется (простым) циклом. Число ребер пути называется длиной пути. Число ребер цикла – длиной цикла. Ребро графа G называется циклическим, если в графе существуют цикл, содержащий это ребро. В противном случае ребро называется нециклическим. Граф называется связным, если любая пара его вершин соединена маршрутом. Простой цикл, содержащий все вершины графа, называется гамильтоновым. Например, цикл В графе H(Y ,P) ему соответствует цикл: Перерисовав граф H(Y ,P) , так, чтобы гамильтонов цикл был в явном виде, получим изображение как показано на рис.10. 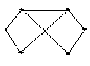 Рис.10. Преобразованный граф H(Y,P) Циклическую подстановку можно записать в виде: y1 y4 y2 y5 y3 y6 4 2 5 3 6 1 2 5 3 6 1 4 5 3 6 1 4 2 3 6 1 4 2 5 6 1 4 2 5 3 1 4 2 5 3 6 Вращение преобразованного графа H(Y,P) вокруг ребер 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 3 2 6 5 4 3 2 1 5 4 6 2 1 3 3 4 5 Очевидно, кроме этих автоморфизмов существуют еще как минимум два очевидных для исходного графа H(Y,P)(рис 9б) Это вращение (поворот на 180)вокруг ребра Это подстановки: 1 2 3 4 5 6 1 2 3 4 5 6 4 5 6 1 2 3 3 2 1 6 5 4 Этим преобразованиям графа H(Y,P) соответствуют графические изображения на рис.11. 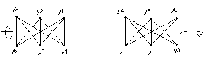 y1 y2 Рис.11. Автоморфизмы вращение графа H(Y,P) Все варианты графов, получаемые с помощью описанных подстановок, являются изоморфными и получаются соответствующей перенумерацией вершин, а в матрице смежности соответствующей перестановкой строк и столбцов. Лекция 7 ОРИЕНТИРОВАННЫЕ И НЕОРИЕНТИРОВАННЫЕ ВЗВЕШЕННЫЕ ГРАФЫ, ИХ ВИДЫ, СВОЙСТВА И МЕТОДЫ ФОРМАЛЬНОГО ОПИСАНИЯ. 1. Подграфы и дополнения Подграфом G′(V′,E′) графа G(V,E) называется граф с множеством вершин V′V и множеством ребер (дуг) Е′Е, каждое из которых инцидентно только вершинам viV′. Подграфом G′(V′,E′), порожденным подмножеством V′V называется граф с множеством вершин V′ и набором ребер (дуг) E′, состоящий из всех ребер (дуг) графа G′, которые соединяют вершины из V′. Остовный подграф G′(V,E′) содержит все вершины G и некоторый набор его ребер (дуг) Е′Е. 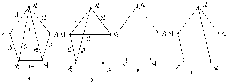 Рис.12. Граф и его подграфы: а) граф G; б) подграфы г) остовный подграф. Граф G′(V,E′) называется дополнением простого графа G(V,E), если ребро 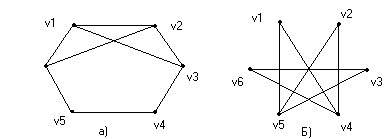 Рис.13. а) граф G; б) граф G , дополняющий графа (до полного графа) 2. Деревья, разрезы, циклы При исследовании сетей военной связи особое место занимают вопросы связности, ее нарушения и восстановления, синтеза структур с максимальной связностью, зависимости связности от структуры графа, выявление узких мест и условий, необходимых (достаточных) для ее нарушения. Непосредственное отношение к этим вопросам имеют такие понятия теории графов как деревья, разрезы, циклы. Граф называется ациклическим, если он не содержит циклов. Деревом Т графа G называется ациклический связный подграф графа G. Остовом графа G называют дерево Т графа G, содержащее все вершины графа G. Связный подграф дерева Т называется поддеревом. Кодерево Т* остова Т графа G является подграфом графа G, содержащим все вершины графа и только те ребра G, которые не входят в Т.  Ребра остова Т называются ветями Т, а ребра соответствующего кодерева Т*- хордами. Ребра остова Т называются ветями Т, а ребра соответствующего кодерева Т*- хордами.Рис.14. Граф, его деревья, остовы, кодеревья. а)- граф G; б)-дерево графа G; в,г)- остовные деревья графа G; д,е)-кодеревья к деревьям; г) и в) соответственно. Нетрудно видеть, что остовное дерево Т содержит n-1 ребер и является минимально связным графом, состоящим из n вершин. Удаление любого ребра приводит к нарушению связности и образованию 2х связных компонент дерева. k- деревом называется ациклический граф, состоящий из k компонент. Если k- дерево является остовным подграфом графа G, то оно называется остовным k-деревом G; k- дерево содержит n-k ребер. Лесом графа G называется остовное k- дерево графа G, где k- число компонент в G. Ко- лес Т* леса Т графа G –это остовный подграф графа G, содержащий те ребра G, которые не входят в Т. 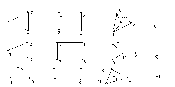 Рис.15. Лес и ко-лес. а)-граф; б)-лес; в)- ко-лес. Если граф содержит n вершин, m ребер и состоит из k- компонент, то ранг графа, обозначаемый через (G), определяется выражением: (G)= n- k, а цикломатическое число, обозначается как (G) и определяется выражением (G) = m – n + k. Из выражений для (G) и (G) следует, что (G) + (G) = m. Рассмотрим граф на рис.15а: k= 3; n = 11; m = 13, отсюда (G) = 11-3 = 8; (G) = 13- 11+3 =5. Базисным циклом графа G относительно хорды остова Т называется цикл, состоящий из ветвей дерева Т и одной из хорд Сi. Как отмечалось ранее, множество ветвей дерева Т содержит n-1 ветвь, множество хорд- m-n+1 ребер соответственно и множество всех циклов равно m-n+1. Множество С1, С2,…, Сm-n+1 циклов графа G относительно хорд Сi остова Т называется базисным множеством циклов графа G относительно Т. Отличительной особенностью базисного цикла Сi является то, что он содержит только одну хорду Сi, которая ни в каких других базисных циклах относительно данного остовного дерева Т не встречается.  Рис.16. Граф, остов и базисные циклы. а)- граф G; б)- остов; в;г;д и е)-базисные циклы 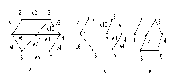 Разрезающим множеством графа S называется такое минимальное множество ребер, удаление которых делает граф G-S несвязным. Минимальность понимается в том смысле, что любое подмножество S′ S не делает граф G несвязным. Разрезающим множеством графа S называется такое минимальное множество ребер, удаление которых делает граф G-S несвязным. Минимальность понимается в том смысле, что любое подмножество S′ S не делает граф G несвязным.Рис.17. Разрезающие множество графа. а)- графG; б)- G-S1; S1 = {e2, e9, e7, e5}; в)- G-S2; S2= { e2, e9, e7}. Пусть V = V1∪ V2 , V1∩ V2= Ø, т.е. V1 и V2 два непересекающихся множества, а вместе содержат все вершины графа. Тогда множество S всех таких ребер, которые имеют одну вершину в V1, а другую в V2, называется разрезом графа G. Отличительной особенностью разреза является то, что множество вершин V1 и V2 определяются изначально, а сам разрез содержит(является пересечением) несколько реберно- непересекающихся разрезающих множеств. Если графы, образованные на множествах вершин V1 и V2 связные, то разрез S= 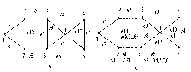 Рис.18. Граф и его разрез.а)-Граф; б)- V1={1,2,7}, разрез S={e2,e6}, множество V2={3,4,5,6,8}.Пусть Т- остов связного графа G, а вi ветвь Т. При удалении ветви из дерева он разделяется на две компоненты Т1, Т2 которые являются деревьями из множеств V1 и V2, а V = V1 V2 , V1∩ V2= Ø. Кроме того Т1и Т2являются остовами графов G1 и G2 , порожденных на множествах вершин V1 и V2. Разрез S= < V1 , V2> является разрезающим множеством графа G. Это разрезающее множество называется базисным множеством графа G по отношению к ветви вi остова Т графа G. Множество всех n-1 базисных разрезающих множеств по отношению к n-1 ветви остова Т связного графа G называется базисным множеством разрезающих множеств графа по отношению к остову Т. Разрезающее множество содержит ровно одну ветвь дерева Т, все остальные его ребра являются хордами. Для установления взаимосвязи между разрезающими множествами, циклами, деревьями и кодеровьями рассмотрим пример. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
     № № | | Т1⊏ | Т2⊐ | Т3⊓ | Т4⊔ | Т5 | Т6 | Т7 | Т8 |
| 1 | Остовы | е1е3е5 | е1е4е5 | е1е3е4 | е3е4е5 | е1е2е3 | е2е4е5 | е2е3е4 | е1е2е5 |
| 2 | Кодеревья | е1е2 | е2е3 | е2е5 | е1е2 | е4е5 | е1е3 | е1е5 | е3е4 |
| 3 | Базисные циклы | е1е3е4е5 | е1е3е4е5 | е1е3е4е5 | е1е3е4е5 | е1е2е4 | е2е3е5 | е1е4е4 | е2е3е5 |
| 4 | Базисные разрезающие множество | е1е4 е2е3е4 е2е4е5 | е1е2е3 е2е3е4 е3е5 | е1е2е3 е3е5 е2е4е5 | е1е2е3 е1е2е5 е1е4 | е1е4 е2е4е5 е3е5 | е1е4 е2е3е4 е2е4е5 | е1е2е5 е3е5 е1е4 | е1е4 е2е3е4 е3е5 |
| 5 | Независимые базисные разрезы | е1е4 | е1е2е3 | е3е5 | е1е2е5 | е2е4е5 | е2е3е4 | | |
| 6 | Независимые цикли | е1е3е4е5 для остовов Т1-Т4 и е1е3е4 и е2е4е5 для Т5-Т8 | |||||||
Лекция 8
ВЗАИМОСВЯЗЬ МАТРИЦ ГРАФОВ
Все введенные ранее понятия, такие как цикл, разрезающее множество, разрез, остовное дерево, кодерево можно представлять набором ребер в виде матрицы-строки, включающей эти ребра.
Если ребро есть, то ставится 1, если нет, то нуль. Совокупность таких матриц-строк, называемых векторами, вместе с определенными над ними алгебраическими операциями умножения и сложения, называют векторным пространством. Через понятие векторного пространства устанавливаются взаимосвязи между матрицами, введенными ранее. Во всех случаях элементами матриц являются нули и единицы.
При изучении взаимосвязей между этими матрицами будем использовать булеву алгебру со сложением по модулю 2.
В этой алгебре : 0·0 = 0; 0·1 = 0; 1·0 = 0; 1·1 = 1; 10 = 1;01= 1;11= 0.
В тех случаях, когда будут использоваться другие алгебры, это будет специально оговариваться.
Все примеры приведены для рассмотренного ранее графа на рис.1.19.
1. Матрица циклов и ее связь с матрицей инцидентности.
Циклы графов, пронумерованные определенным порядком, можно представить матрицей циклов С.
| | | е1 | е2 | е3 | е4 | е5 |
| | С1 | 1 | 1 | 0 | 1 | 0 |
| С= | С2 | 0 | 1 | 1 | 0 | 1 |
| | С3 | 1 | 0 | 1 | 1 | 1 |
Матрица циклов имеет m столбцов(по числу ребер ) и количество строк, равное числу циклов (m-n+1).
Матрицу циклов называют еще цикломатической матрицей.
Строку матрицы С: называют также циклическим вектором графа G. Как видно из матрицы циклов, вектор С3 = С1 С2 =11010 01101 = 10111, является линейной комбинацией векторов С1 и С2.
Это означает . что из множества всех циклических векторов можно выделить базисные, по отношению к определенному остовному дереву.
Пусть это дерево состоит из ребер {e1, e2 ,e3 }, тогда хордами будут ребра е4 и е5 . Вспомним , что базисный цикл состоит из одной хорды и ветвей остовного дерева. Переставим столбцы матрицы циклов так, чтобы первым строкам и столбцам соответствовали хорды остовного дерева:
| | | е4 | е5 | е1 | е2 | е3 |
| Сf= | е4 | 1 | 0 | 1 | 1 | 0 |
| | е5 | 0 | 1 | 0 | 1 | 1 |
I Сft
Таким образом, базисная матрица циклов Сf является подматрицей матрицы циклов C и включает только циклы, определяемые хордами выбранного остовного дерева.
Эту матрицу можно записать в виде :Сf= [ I | Cft ], где I – единичная матрица хорд, а элементами матрицы Cft являются ветви выбранного остовного дерева, по отношению к которому определены базисные циклы.
Кроме того, матрицу Сf можно представить состоящей из двух блоков Cf = (С11 С12) , где С11= I , С12= Cft.
Запишем матрицу инцидентности графа G, переставив столбцы, как и у базисной матрицы циклов:
| | | е4 | е5 | е1 | е2 | е3 |
| | V1 | 0 | 0 | 1 | 1 | 1 |
| A= | V2 | 1 | 0 | 1 | 0 | 0 |
| | V3 | 1 | 1 | 0 | 1 | 0 |
| | V4 | 0 | 1 | 0 | 0 | 1 |
Так как ранг матрицы инцидентности равен n-1 , где n- число вершин, то можно выделить неособенную матрицу в правом верхнем углу А12 размерностью (n-1)х(n-1), состоящую из ветвей остовного дерева( так же ранга n-1) и представить матрицу инцидентности А в виде блочной матрицы:
| А= | А11 | А12 | , где | А11= | 0 | 0 | | 1 | 1 | 1 |
| | | 1 | 0 | ; А12= | 1 | 0 | 0 | |||
| А21 | А22 | 1 | 1 | | 0 | 1 | 0 |
А21=| 0 1 | A22= | 0 0 1 |
Матрица А11 представляет кодерево, состоящее из хорд е4 и е5 , матрица А12 представляет дерево по отношению к которому определяются базисные циклы.
Матрицы А21 и А22 линейно зависят от А11 и А12 , выражаются через них в виде суммы элементов строк по модулю 2, что легко проверяется непосредственным сложением. Доказано , что А . С' = 0.
В наших новых обозначениях это выражение можно переписать следующим образом :
А11 А12 I
А21 А22 C12 =0
Проверим его непосредственно для графа G:
0 0 1 1 1 1 0 00
А11 А12 I 1 0 1 0 1 0 1 00
А∙С = А21 А22 C12 = 1 1 0 1 0 х 1 0 = 00 =0.
0 1 0 0 1 1 1 00
0 1 00
Из этого же выражения следует , что :
А11 .I + A12 . C′12 = 0
Поскольку матрица А12 неособенная то :
С12= А12-1 . А11 , т.ематрицу циклов ( транспонированную) можно получить из матрицы инцидентности представив ее в виде блоков, состоящих из подматрицы дерева и подматрицы кодерева, т.е. из ветвей остовного дерева и хорд кодерева.
Рассмотрим пример для нашего графа :
1 1 1 1 0
А12 = 1 0 0 |A12| =-1 х = -1 =1
0 1 0 0 1
Определитель А12 вычислен путем разложения его по элементам третьего столбца, с учетом применения алгебры по модулю 2.
Для обращения матрицы существуют стандартные процедуры (напримерmathcad), но мы воспользуемся классическим методом.
а1а2 а3 в2с3-в3с2 а3с2-а2с3 а1в3-а3в2
А= в1 в2 в3; А-1= 1/ |A|в3с1-в1с3 а1с3-а3с1 а3в1-а1в3
с1 с2 с3 в1с2-в2с1 а2с1-а1с2 а1в2-а2в1
подставив в выражение элементы матрицы А12, получим,
0 1 0 1 1 1
А12-1 = 0 0 1 ; проверим А12. А12-1 = 1 0 0 х
1 1 1 0 1 0
0 1 0 1 0 0
х 0 0 1 = 0 1 0
1 1 1 0 0 1
найдем траспонированную матрицу С′12
0 1 0 0 0 1 0
С′12= А12-1 . А11= 0 0 1 . 1 0 = 1 1
1 1 1 1 1 0 1
1 1 0
откудаС12= 0 1 1 .
Присоединив слева единичную матрицу, получим матрицу базисных циклов:
1 0 1 1 0
Сf= ( I / C12)=
0 1 0 1 1
Таким образом, задавшись остовным деревом, из матрицы инциденций можно получить матрицу базисных циклов.
Однако, проще это делать “ вручную”:
Пусть остовное дерево включает ветви е1, е2, е3, а хорды кодеревы е4 и е5. Добавляя к дереву хорду е4получаем цикл е2е3е4, добавляя хорду е5, получаем цикл е1е2е5. Получив циклы, записываем их в матрицу циклов.
| | e1 | e2 | e3 | e4 | e5 |
| Сf = | 1 | 1 | 0 | 1 | 0 |
| | 0 | 1 | 1 | 0 | 1 |
Поскольку остовное дерево все равно необходимо набирать вручную при вводе в ЭВМ, то и матрицу циклов можно сразу набрать вручную, так как при добавлении одной (очередной) хорды получается ровно один (очередной) базовой цикл.

