Методологические основы моделирования

• Название: Методологические основы моделирования
• Анкор: sobrannye_lektsii_1_2.docx
• Дата: 07.03.2018
• Размер: 2.94 Mb.
• Имя файла: sobrannye_lektsii_1_2.docx
• Тип: Лекция; #16341
• страница: 7 из 19

Рис.23. Граф и его блоки. а) граф G, б,в,г,д)- блоки графа G₁ ,G₂ ,G₃ , G₄. v₁ иv₂ – точки сочленения, в) –мост G₂ (ребро 1 v₂>). г) и д) – клики G₃ иG₄

Вершинной связностью æ(G) называют наименьшее число вершин, удаление которых приводит к несвязному (пустому) графу.

Реберной связностью λ(G) называют минимальное число ребер, удаление которых приводит к несвязному или тривиальному графу. Другими словами, λ(G)- это число ребер в разрезе с минимальным числом ребер. Для ее определения достаточно рассмотреть базисное множество разрезов.

Смешанная связность σ(G)- минимальное число вершин и ребер, удаление которых приводит к несвязному графу.

Для характеристики смешанной связности σ (G) используют понятие пары связности, под которой понимают упорядоченную пару(a,b) , таких целых неотрицательных чисел, что найдется множество, содержащее а вершин и b ребер, удаление которых делает граф несвязным, и не найдется множества с а-1 вершинами и в ребрами или а вершинами и b-1 ребрами, обладающего этим же свойством. Так, пары (æ,0) и (0, λ)являются парами связностей. Эта функция называется функцией связности графа G.

Вершинная связность важна при оценке живучести в условиях воздействия оружия противника на узлы связи, реберная – при оценке помехозащишености сети, смешанная при воздействии средств РЭБ (помех и оружия) на сети (системы) связи.

Важное значение при изучении связности имеет степень вершин d(v_i) и минимальная степень вершин графа δ(G).

Доказано, что для любого графа выполняются:

æ(G) ≤ λ(G) ≤ δ (G)

кроме того, показано, что ограничения накладываемые на λ, δ и æ нельзя улучшить.

Если же граф G имеет n вершин и δ (G) ≥ [n / 2] ,то λ(G) = δ(G) и наибольшая связность графа равна [2m / n], если m ≥ n-1 .

Рис.24. Граф, для которого æ(G) = 2{v₁ и v₂ или v₇ и v₈},

λ(G) = 3 { 1v₇>,2v₇>,2v₈>}, σ (G)= 2 {v₂ и 1,v₇>} или {v₇ и 2,v₈>}.
С точки зрения воздействия противника это означает, что для нарушения связности сети необходимо:

-уничтожить узлы v₁ и v₃;

-уничтожить узлы v₇ и v₈;

-подавить каналы или уничтожить линии связи, соответствующие на модели ребрам 1v₇>, 2v₇>, 2v₈>;

-уничтожить узел v₂ и подавить 1v₇>;

-уничтожить узел v₇ и подавить 2v₈>.

Пары связности графа: (0,3); (1,1); (2,0)функция связности показана на рис.25.

σ(æ)
3
2
1
0	1	2		æ

Рис.25. Функция связности F(æ) графа G

Граф называется k- вершинно-связным, если æ(G) ≥ k и k реберно- связным, если λ(G) ≥ k .

Связность графа достаточно жестко коррелируется с числом вершинно и реберно непересекающихся путей, разрезами точками сочления и сечениями по ребрам и вершинам (разделяющими множествами). Рассмотрим эти вопросы более подробно.

Под сечением по вершинам (разделяющим множеством) понимается множество вершин, удаление которых приводит к несвязному графу.

Таким образом, вершинная связность æ(G) является минимальным сечением по вершинам ( разделяющим множеством).

Так на рис.26. сечением по вершинам (разделяющим множеством), может быть множество {v₁, v₂, v₇, v₈}, состоящее из двух минимальных сечений множеств {v₁, v₂} и { v₇, v₈}, определяющих вершинную связность графа.

Пусть u и v- две различные вершины связного графа. u и v, называются вершино- пересекающимися, если у них нет общих вершин, отличных от u и v, и реберно- пересекающимся, если у них нет общих ребер. Множество S вершин, ребер, или ребер и вершин разделяет u и v, если u и v принадлежат различным компонентам графа G-S.

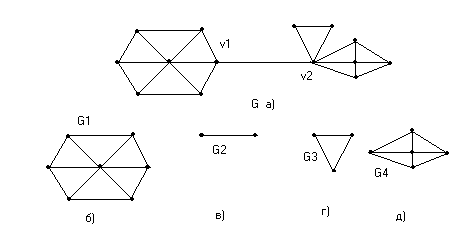
G₁G₂
Рис.26. Граф G(V,E) и разделяющее множество вершин и ребер S.

На рис.1.26. приведен граф G, разделяющее множество S={v₁, v₂, v₇, v₈ и ребра, показанные пунктиром}, и граф G-S содержащий две компоненты G₁ и G₂ с вершинами {v₃, v₄, v₅, v₆} и {v₉, v₁₀, v₁₁, v₁₂} и ребрами, показаными сплошными линиями.

В разделенных компонентах графа G, например G₁ и G₂ рассматривают три пары объектов:

выделенные вершины u и v , например u = v₅; v = v₁₀ ;

произвольные вершины u и v , например, v_i ЄV₁и v_jЄ V₂, где V₁={ v_3, v_4, v_5, v_6,} , V₁={ v_9, v_10, v_11, v_12,}.

два множества вершин V₁ и V₂.

Это разделение можно произвести, удаляя вершины, ребра или вершины и ребра, т.е. тремя способами.

Таким образом, между связностью графа и числом непересекающихся путей в зависимости от способов выделения вершин и разделяющего их множества существуют 9 вариантов взаимозависимостей.

Кроме того, если рассматривать результаты отдельно для ориентированных и неориентированных графов, то их 18.

Все эти варианты Харари выделил в класс теорем Менгера.

Рассмотрим их без доказательства и проиллюстрируем на примерах только основные из них.

Теорема 1. Наименьшее число вершин, разделяющих две несмежные вершины s и t , равно наибольшему числу вершинно- непересекающихся простых (s-t) путей).

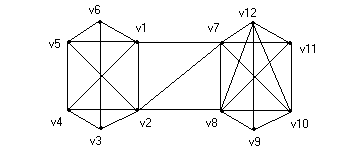
Так на рис.38 для вершин s = v₁ , t = v₁₁ наименьшее число вершин, которые их разделяют 3. Это { v_5, v_6, v₇}.

Вершинно – непересекающихся путей также 3. Это один из путей, ведущих из вершины s в t через узлы v₅ , v₆ , v₇;



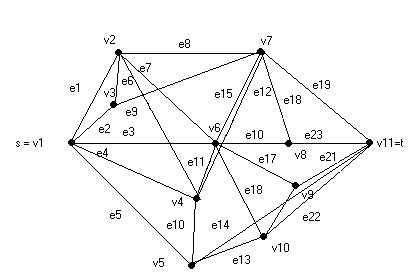
Рис.27.Граф для иллюстрации класса теорем Менгера.

Пять реберно- непересекающихся путей, приведены ниже:

¹_st= 1,e₈,e₁₉> = 1,v₂,v₇,v₁₁>

²_st= 3,e₁₀,e₂₃> = 1,v₆,v₈,v₁₁>вершинно- непересекающиеся пути

³_st= 5,e₁₄> = 1,v₅,v₁₁>
⁴_st =e₂,e₉,e₁₅,e₁₇,e₂₁>= < v₁,v₃,v₇,v₆,v₉,v₁₁>вершинно- зависимые

⁵_st=4,e₁₁,e₁₈,e₂₂>=1,v₄,v₆,v₁₀,v₁₁>пути
Для реберно- непересекающихся путей ⁴_st , ⁵_st существуют общие с ¹_st, ²_st вершины v₆ и v₇.

Общие для путей вершины обведены пунктиром.

Теорема 2. Граф k- связен тогда и только тогда, когда любая пара вершин соединена по крайней мере kвершинно- непересекающимися путями.

Связь между теоремами 1 и 2 устанавливается, если ввести понятие локальной связности.

Локальной связностью æ(u, v) двух несмежных вершин, u и v графа G называется наименьшее число вершин, удаление которых разделяет u и v .

В этом случае для произвольных вершин u и v справедливо равенство æ(u, v) = ₀(u,v), где ₀(u,v)- наибольшее число вершинно-непересекающихся путей, соединяющих u и v.

Для неполных графов G соотношение, связывающее теоремы 1 и 2 имеет вид: æ(G) = min æ(u, v), где минимум берется по всем парам несмежных вершин u и v.

Для полного графа это равенство справедливо всегда.

Возьмем произвольные несмежные вершины u = v₁ и v = v₇. (рис.27.)

Определим ₀(u,v) :

u = v₁ v₂ v₇= v; u = v₁ v₃ v₇= v; u = v₁ v₆ v₇= v; u = v₁ v₄ v₇= v; u = v₁ v₅ v₁₁ v₇= v ₀(u,v) = 5, это вполне очевидно, поскольку из вершины u, исходит только 5 ребер к независимым вершинам;

F(u) = { v₂, v₃, v₄, v₅,v₆}, степень d(u)=5.

Пусть теперь u = v₃ , v = v₄. Определим ₀(u,v);

u = v₃ v₂ v₄= v; u = v₃ v₁ v₄= v; u = v₃ v₇ v₄= v ₀(u,v)= 3

Это тоже ожидаемый результат, поскольку степень вершины d(v₃) = 3, следовательновершинно-независимых путей, исходящих из нее, не может быть более трех.

Вершина v₄ имеет степень d(v₄) = 5 и поэтому не накладывает ограничений .

Возьмем в качестве несмежных вершины с минимальными степенями.

Это вершины u = v₃ и v = v₈ и определим ₀(u,v);

u = v₃ v₇ v₈= v; u = v₃ v₆ v₈= v; u = v₃ v₁ v₅ v₁₁ v₈ = v

Вершина v₃ имеет степень d(v₃)=3 и связана с вершинами {v₁ v₆ v₇}; v = v₈ также имеет степень d(v₈)=3 и связана с вершинами v₆ , v₇ ,v₁₁.

Вершины v₆ и v₇ являются смежными и для v = v₈ .

Для того, чтобы эти вершины были связаны тремя независимыми путями, необходимо, чтобы вершина v₁, смежная с вершиной v₃ и вершина v₁₁, смежная с v₈ были связаны вершинно-независимыми путям.

Такой путь есть v₁ , v₅ ,v₁₁ , причем вершина v₅ не входит в первые два пути.

Для двух несмежных вершин с минимальными степенями получено ₀(u,v), равное наибольшему числу вершинно- независимых путей 3.

Следуя теореме 2, можно заключить, что граф на рис.27. является 3- связным (вершинно), т.е. æ(G) = min æ(u, v)= 3 ,и кроме того показано, что æ(G) ≤ δ(G) = min d(v_i)=3; в данном случае имеет место равенство.

Таким образом, соотношение æ(G) = min æ(u, v), связывающее теоремы 1 и 2, кроме того устанавливает зависимость между глобальными æ(G) и локальными æ(u, v) характеристиками вершинной связности.

Следует обратить внимание на то, что во-первых необязательно минимальное число независимых путей находится между вершинами с минимальными степенями и во-вторых, задача определения минимального локального показателя связности, а следовательно и связности не является тривиальной.

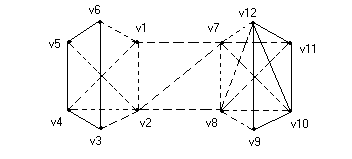
Рассмотрим пример на рис.28, где показаны два изоморфных графов G₁, G₂



G₁ G₂


Рис.28. Графы G₁ и G₂ для иллюстрации сложного случая определения æ(G) и min æ(u, v).

Изоморфность проверяется подстановкой:
t = 1 2 3 4 5 6 7 8 9 10 11 12

1 5 3 4 2 6 7 11 9 10 8 12
Каждая из вершин, кроме v₃ и v₁₀, имеет степень 3, а вершины v₃ иv₁₀ имеют степень 4.

Вместе с тем , вершины v₃ и v₁₀ являются точками сочленения, а ребро 3 и v₁₀> - мостом, так что вершинная и реберная связности равны 1, т.е. æ(G) =λ(G)= 1, кроме того σ(G)= 1. При этом пара связности (а,в) равна(1,0) или (0,1), т.е. необходимо удалить либо одну вершину(v₃ или v₁₀) или одно ребро 3v₁₀>.

Теорема 3. Для любых двух вершин графа наибольшее число реберно – непересекающихся путей, соединяющих их, равно наименьшему числу ребер, разделяющих эти вершины.

Из рис.27. видно, что вершины s и t можно разделить , удалив 5 ребер и не меньше, и что наибольшее число непересекающихся по ребрам (s – t) путей равно 5.

Проиллюстрируем это.

Из вершины s = v₁ исходит ровно 5 ребер E₁= { e₁, e₂, e₃, e₄, e₅}. В вершину t = v₁₁ заходят ровно 5 ребер E₂= { e₁₉, e₂₃, e₂₁, e₂₂, е₁₄ }.

Между вершинами s и t существуют следующие реберно- независимые пути, включающие ребра множества Е₁, в качестве начальных и ребра множества Е₂ в качестве конечных.

^1st = e₁ e₈ e₁₉

²_st = e₃ e₁₀ e₂₃

³_st = e₅ e₁₄

⁴_st= e₂e₉e₁₅e₁₇e₂₁

⁵_st = e₄e₁₁ e₁₈ e₂₂

Е₁Е₂
Множества Е₁ и Е₂ обведены пунктирными линиями. Остальные ребра путей ⁱ_st (i =1, 5) также являются различными.

В пути ¹_st ребро е₈ можно заменить ребрами е₇е₁₅, т.е. между множествами Е₁ и Е₂ существует более 5 реберно- независимых путей, поэтому наименьшее число ребер, определяющих число реберно- непересекающихся путей в данном случае определяется минимальной степенью вершин s и t .

В данном случае обе они равны 5, следовательно вершины s и t можно разделить, удалив 5 ребер и наибольшее число непересекающихся по ребрам (s – t ) путей также равно 5, что подтверждает правильность теоремы 3.

Поиск и определение реберно–независимых путей важен прирешения задачи оценки вероятности передачи сообщений, следующих в потоке заданной интенсивности, за время не более требуемого в условиях подавления каналов радиосвязи помехами.

Теорема 4. Для любых двух непересекающихся непустых множеств вершин V₁ и V₂ наибольшее число вершинно- непересекающихся путей, соединяющих V₁ и V₂ равно наименьшему числу вершин, разделяющих V₁ и V₂ , при условии, что ни одна из вершин множества V₁ не должна быть смежной с вершинами множества V₂ .

На рис 38 условиям теоремы 4 соответствуют множества;

V₁= {v₁, v₂, v₃, v₄}

V₂= {v₈, v₉, v₁₀, v₁₁}

Множество V₃= {v₅, v₆, v₇ }, разделяющее множества V₁ и V₂,включает три вершины, через которые проходят три вершинно- независимых пути, соединяющих вершины множеств V₁ и V₂, и других вершинно – независимых путей нет.

Возьмем в качестве другого примера V₁= {v₂, v₃, v₆, v₇}, которому по условиям теоремы 4 может соответствовать только множество V₂= {v₅}.

Множество V₃ , разделяющее множества V₁ и V₂, включает 6 вершин V₃= {v₁, v₄, v₆, v₉, v₁₀,v₁₁}однако, минимальное число вершин, которое разделяет множества V₁ и V₂ –это множество вершин, смежных с v₅ {v₁,v₄,v₁₀,v₁₁}содержит 4 вершины, следовательно и число вершинно-независимых путей из множества V₁ в V₂ равно 4.

Определение числа вершинно-независимых путей важно при моделировании поведения сети в условиях огневого воздействия противника на узлы связи.

С помощью теорем 1- 4 устанавливаются два понятия связности – вершинная æ(G) и реберная λ(G), а также определяются их взаимозависимости, т.е. каждый граф можно характеризовать парой связностей, точно также можно ввести понятие ‘’ пары связностей’’ для двух выделенных вершин u и v .

Следующая теорема устанавливает количественные зависимости между составляющими введенного понятия смешанной связности σ(G).