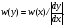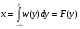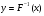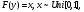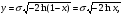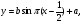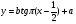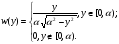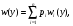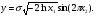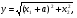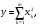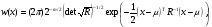Методологические основы моделирования
 Скачать 2.94 Mb. Скачать 2.94 Mb.
|
Лекция 3 ОСНОВНЫЕ ЭТАПЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СИСТЕМ И ПРОЦЕССОВ 1.Основные этапы математического моделирования Первым этапом математического моделирования является постановка задачи, определение объекта и целей исследования, задание критериев(признаков) изучения объектов и управления ими. Неправильная или неполная постановка задачи может свести на нет результаты всех последующих этапов. Вторым этапом моделирования является выбор типа математической модели, что является важнейшим моментом, определяющим направление всегоисследования. Обычно последовательно строится несколько моделей.Сравнение результатов их исследования с реальностью позволяет установитьнаилучшую из них. На этапе выбора типа атематической модели при помощианализа данных поискового эксперимента устанавливаются: линейность илинелинейность, динамичность или статичность, стационарность илинестационарность, а также степень детерминированности исследуемого объектаили процесса.Процесс выбора математической модели объекта заканчивается еепредварительным контролем, который также является первым шагом на путик исследованию модели. При этом осуществляются следующие видыконтроля (проверки): размерностей; порядков; характера зависимостей;экстремальных ситуаций; граничных условий; математической замкнутости;физического смысла; устойчивости модели. Контроль размерностей сводится к проверке выполнения правила,согласно которому приравниваться и складываться могут только величиныодинаковой размерности. Контроль порядков величин направлен на упрощение модели. При этом пределяются порядки складываемых величин и явно малозначительныеслагаемые отбрасываются. Анализ характера зависимостей сводится к проверке направления искорости изменения одних величин при изменении других. Направления искорость, вытекающие из ММ, должны соответствовать физическому смыслузадачи. Анализ экстремальных ситуаций сводится к проверке наглядного смысла решения при приближении параметров модели к нулю или бесконечности. Контроль граничных условий состоит в том, что проверяетсясоответствие ММграничным условиям, вытекающим из смысла задачи. Приэтом проверяется, действительно ли граничные условия поставлены и учтеныпри построении искомой функции и что эта функция на самом делеудовлетворяет таким условиям. Анализ математической замкнутости сводится к проверке того, что ММдает однозначное решение. Анализ физического смысла сводится к проверке физическогосодержания промежуточных соотношений, используемых при построении ММ. Проверка устойчивости модели состоит в проверке того, чтоварьирование исходных данных в рамках имеющихся данных о реальномобъекте не приведет к существенному изменению решения. 2. Понятие о вычислительном эксперименте В настоящее время основным способом исследования ММ и проверки еекачественных показателей служит вычислительный эксперимент. Вычислительным экспериментом называется методология и технологияисследований, основанные на применении прикладной математики и ЭВМ кактехнической базы при использовании ММ. Вычислительный экспериментосновывается на создании ММ изучаемых объектов, которые формируютсяс помощью некоторой особой математической структуры, способной отражатьсвойства объекта, проявляемые им в различных экспериментальных условиях, ивключает в себя следующие этапы. 1. Для исследуемого объекта строится модель, обычно сначала физическая,фиксирующая разделение всех действующих в рассматриваемом явлениифакторов на главные и второстепенные, которые на данном этапе исследованияотбрасываются; одновременно формулируются допущения и условияприменимости модели, границы, в которых будут справедливы полученныерезультаты; модель записывается в математических, терминах, как правило,в виде дифференциальных или интегро-дифференциальных уравнений;создание ММ проводится специалистами, хорошо знающими данную областьестествознания или техники, а также математиками, представляющими себевозможности решения математической задачи. 2. Разрабатывается метод решения сформулированной математическойзадачи. Эта задача представляется в виде совокупности алгебраическихформул, по которым должны вестись вычисления и условия, показывающиепоследовательность применения этих формул; набор этих формул и условийносит название вычислительного алгоритма. Вычислительный экспериментимеет многовариантный характер, так как решения поставленных задач частозависят от многочисленных входных параметров. Тем не менее, каждыйконкретный расчет в вычислительном эксперименте проводится прификсированных значениях всех параметров. Между тем в результате такогоэксперимента часто ставится задача определения оптимального наборапараметров. Поэтому при создании оптимальной установки приходитсяпроводить большое число расчетов однотипных вариантов задачи,отличающихся значением некоторых параметров. В связи с этим приорганизации вычислительного эксперимента можно использовать эффективные численные методы. 3. Разрабатываются алгоритм и программа решения задачи на ЭВМ.Программирование решений определяется теперь не только искусством иопытом исполнителя, а перерастает в самостоятельную науку со своимипринципиальными подходами. 4. Проведение расчетов на ЭВМ. Результат получается в виде некоторойцифровой информации, которую далее необходимо будет расшифровать.Точность информации определяется при вычислительном экспериментедостоверностью модели, положенной в основу эксперимента, правильностьюалгоритмов и программ (проводятся предварительные «тестовые» испытания). 5. Обработка результатов расчетов, их анализ и выводы. На этом этапемогут возникнуть необходимость уточнения ММ (усложнения или, наоборот,упрощения), предложения по созданию упрощенных инженерных способоврешения и формул, дающих возможности получить необходимую информациюболее простым способом. Вычислительный эксперимент приобретает исключительное значение в техслучаях, когда натурные эксперименты и построение физической моделиоказываются невозможными. Особенно ярко можно проиллюстрироватьзначение вычислительного эксперимента при исследовании влияния городскойзастройки на параметры распространения радиосигнала. В связис интенсивным развитием систем мобильной связи данная задача в настоящеевремя является особенно актуальной. С целью снижения затрат при частотно-территориальном планировании производится оптимизация частотно-территориального плана с учетом таких факторов как рельеф местности,конфигурация городской застройки, атмосферные воздействия. Кроме этого,с учетом динамичности развития города необходимо постоянное уточнениесоответствующих моделей. То, что принято называть уровнем сигнала (средняянапряженность электромагнитного поля) представляет собой результатсложного взаимодействия физических процессов, протекающих прираспространении сигнала: прохождение сигнала сквозь здания и сооружения;воздействие на сигнал помех искусственного и естественного происхождения;атмосферная рефракция сигнала; отражения сигнала от зданий и от земнойповерхности; потери энергии сигнала в осадках и др. В данном случаеокружающую среду можно исследовать, строя соответствующую ММ, котораядолжна позволять предсказывать уровень сигнала при заданной конфигурациизастройки, рельефе местности, погодных условиях и т. п. Масштабы средыраспространения сигнала настолько грандиозны, что эксперимент даже в одномкаком-то регионе требует существенных затрат. Таким образом, глобальный эксперимент по исследованиюраспространения сигнала возможен, но не натурный, а вычислительный,проводящий исследования не реальной системы (окружающей среды), а ее ММ. В науке и технике известно немало областей, в которых вычислительныйэксперимент оказывается единственно возможным при исследовании сложныхсистем. Пригодность ММ для решения задач исследования характеризуется тем,в какой степени она обладает так называемыми целевыми свойствами,основными из которых являются адекватность, устойчивость ичувствительность. 3.Оценка свойств моделей Оценка адекватности В общем случае под адекватностью понимают степень соответствиямодели тому реальному явлению или объекту, для описания которого онастроится. Вместе с тем, создаваемая модель ориентирована, как правило, наисследование определенного подмножества свойств этого объекта. Поэтомуможно считать, что адекватность модели определяется степенью еесоответствия не столько реальному объекту, сколько целям исследования.В наибольшей степени это утверждение справедливо относительно моделейпроектируемых систем (т. е. в ситуациях, когда реальная система вообще несуществует). Тем не менее, во многих случаях полезно иметь формальноеподтверждение (или обоснование) адекватности разработанной модели. Одиниз наиболее распространенных способов такого обоснования – использованиеметодов математической статистики [6, 7, 39]. Суть этих методов заключаетсяв проверке выдвинутой гипотезы (в данном случае - об адекватности модели)на основе некоторых статистических критериев. При этом следует заметить,что при проверке гипотез методами математической статистики необходимоиметь в виду, что статистические критерии не могут доказать ни однойгипотезы - они могут лишь указать на отсутствие опровержения. Итак, каким же образом можно оценить адекватность разработанноймодели реально существующей системе? Процедура оценки основана на сравнении измерений на реальной системеи результатов экспериментов на модели и может проводиться различнымиспособами. Наиболее распространенные из них: – по средним значениям откликов модели и системы; – по дисперсиям отклонений откликов модели от среднего значенияоткликов системы; – по максимальному значению относительных отклонений откликовмодели от откликов системы. Названные способы оценки достаточно близки между собой, по сути,поэтому ограничимся рассмотрением первого из них. При этом способепроверяется гипотеза о близости среднего значения наблюдаемой переменнойY среднему значению отклика реальной системы Y* . В результате N опытов на реальной системе получают множествозначений (выборку) Y* . Выполнив M N экспериментов на модели, такжеполучают множество значений наблюдаемой переменной Y . Затем вычисляются оценки математического ожидания и дисперсииоткликов модели и системы, после чего выдвигается гипотеза о близостисредних значений величин Y* и Y (в статистическом смысле). Основой дляпроверки гипотезы является t -статистика (распределение Стьюдента). Ее значение, вычисленное по результатам испытаний, сравниваетсяс критическим значением kp t , взятым из справочной таблицы. Есливыполняется неравенство n kp t <t , то гипотеза принимается. Необходимо ещераз подчеркнуть, что статистические методы применимы только в том случае,если оценивается адекватность модели существующей системе. На проектируемой системе провести измерения, естественно, не представляетсявозможным. Единственный способ преодолеть это препятствие заключаетсяв том, чтобы принять в качестве эталонного объекта концептуальную модельпроектируемой системы. Тогда оценка адекватности программнореализованной модели заключается в проверке того, насколько корректно онаотражает концептуальную модель. Оценка устойчивости При проверке адекватности модели как существующей, так ипроектируемой системы реально может быть использовано лишь ограниченное подмножество всех возможных значений входных параметров (рабочейнагрузки и внешней среды). В связи с этим для обоснования достоверностиполучаемых результатов моделирования большое значение имеет проверкаустойчивости модели. В теории моделирования это понятие трактуетсяследующим образом. Устойчивость модели - это ее способность сохранять адекватность приисследовании эффективности системы на всем возможном диапазоне рабочейнагрузки, а также при внесении изменений в конфигурацию системы. Каким образом может быть оценена устойчивость модели? Универсальнойпроцедуры проверки устойчивости модели не существует. Разработчиквынужден прибегать к методам «для данного случая», частичным тестам издравому смыслу. Часто полезна апостериорная проверка. Она состоитв сравнении результатов моделирования и результатов измерений на системепосле внесения в нее изменений. Если результаты моделирования приемлемы,уверенность в устойчивости модели возрастает. В общем случае можно утверждать, что чем ближе структура моделиструктуре системы и чем выше степень детализации, тем устойчивее модель. Устойчивость результатов моделирования может быть также оценена методамиматематической статистики. Здесь уместно вспомнить основную задачуматематической статистики, которая заключается в том, чтобы проверитьгипотезу относительно свойств некоторого множества элементов, называемогогенеральной совокупностью, оценивая свойства какого-либо подмножествагенеральной совокупности (тоесть выборки). В генеральной совокупностиисследователя обычно интересует некоторый признак, который обусловленслучайностью и может иметь качественный или количественный характер.В данном случае именно устойчивость результатов моделирования можнорассматривать как признак, подлежащий оценке. Для проверки гипотезыоб устойчивости результатов может быть использован критерий Уилкоксона,который служит для проверки того, относятся ли две выборки к одной и той жегенеральной совокупности (т. е. обладают ли они одним и тем жестатистическим признаком). Например, в двух партиях некоторойпродукции измеряется определенный признак и требуется проверить гипотезуо том, что этот признак имеет в обеих партиях одинаковое распределение;другими словами, необходимо убедиться, что технологический процесс отпартии к партии изменяется несущественно. При статистической оценкеустойчивости модели соответствующая гипотеза может быть сформулированаследующим образом: при изменении входной (рабочей) нагрузки илиструктуры ММ закон распределения результатов моделирования остается неизменным. Оценка чувствительности Очевидно, что устойчивость является положительным свойством модели.Однако если изменение входных воздействий или параметров модели(в некотором заданном диапазоне) не отражается на значениях выходныхпараметров, то польза от такой модели невелика. В связи с этим возникаетзадача оценивания чувствительности модели к изменению параметров рабочейнагрузки и внутренних параметров самой системы.Такую оценку проводят по каждому параметру модели в отдельности.Основана она на том, что обычно диапазон возможных изменений параметраизвестен. Данные, полученные при оценке чувствительности модели, могутбыть использованы, в частности, при планировании экспериментов: большеевнимание должно уделяться тем параметрам, по которым модель являетсяболее чувствительной. Роль, которую играет математическое моделирование, безусловно, зависитот характера рассматриваемой задачи, мастерства экспериментатора,располагаемого времени и отпущенных средств, а также от выбранной модели. Необходимо постоянно иметь в виду первоначальную задачу. Самаяраспространенная ошибка связана с тем, что теряется из виду основная цель. Другой ошибкой является переход к моделированию при отсутствиидостаточного количества данных о поведении системы в прошлом. Известен метод последовательного решения задачи,состоящий из следующих этапов: 1) формулировка задачи; 2) накопление экспериментальных данных (в том числе, анализ возможныхошибок в системе регистрации данных, а в некоторых случаях разработка новойсистемы регистрации, которая будет давать соответствующие данные); 3) определение влияния рабочих параметров системы или процесса (анализслучайных колебаний процесса с целью выяснения статистической зависимостирезультатов от соответствующих параметров); 4) составление методики эксперимента (например, изменение параметровс целью определения фактического воздействия на результат); 5) уменьшение числа «рабочих» параметров (оставление лишь тех параметров,к изменению которых результаты наиболее чувствительны); 6) выяснение ограничений, свойственных методу. Одной из основных ошибок при математическом моделировании являетсястремление к искажению реальных условий, т. е. условий, наблюдаемыхв естественной или технической системе. Эти искажения часто делаются для того,чтобы воспользоваться определенной, уже созданной для другой цели моделью. Такой порядок неразумен, даже если он кажется целесообразным. В отличие оттаких типовых методов, как, например, методы линейного программирования,математическое моделирование требует применения довольно утомительныхопераций, поскольку в данном случае необходимо выводить специальныематематические уравнения, адекватно описывающие рассматриваемую реальнуюсистему. Задача экспериментатора не ограничивается построением модели. Послеразработки модели в нее необходимо ввести определенную информацию, чтобыпроверить, насколько приближаются воспроизводимые ею данные к ранеезарегистрированным экспериментальным данным, которые соответствуют введеннойинформации. Лишь в том случае, когда воспроизводимые данные достаточно близкик исходной информации, можно будет гарантировать определенный успех прииспользовании модели для экспериментирования. Лекция 4.
Под моделированием случайной величины (СВ) ξ принято понимать процесс получения на ЭВМ ее выборочных значений ξ1,…, ξN. Величины ξ1,…, ξN статистически независимы и имеют одинаковое распределение вероятностей, совпадающее с распределением СВ ξ. Практически любая задача статистического моделирования содержит в качестве самостоятельного этапа получение реализаций СВ с заданными законами распределения. Исходным материалом для формирования на ЭВМ СВ с различными законами распределения служат равномерно распределенные в интервале (0, 1) случайные числа, которые вырабатываются на ЭВМ программным датчиком случайных чисел. Программы для получения псевдослучайных величин ξ с равномерным законом распределения входят в математическое обеспечение современных ЭВМ. Рассматриваются основные методы моделирования СВ, применяемые при моделировании систем связи, такие как методы нелинейного преобразования, суперпозиции, Неймана, кусочной аппроксимации. Рассмотрим сначала общие приемы получения СВ с заданным законом распределения из равномерно распределенных случайных чисел.
2.1. Метод нелинейного преобразования, обратного функции распределения Задачи моделирования случайных процессов, имеющих место в системах передачи и обработки сигналов, часто приводят к необходимости получения СВ с негауссовским законом распределения. Наиболее эффективным аналитическим методом получения негауссовских СВ является метод монотонного нелинейного преобразования (метод обратных функций). Найдем закон распределения величины y полученной нелинейным преобразованием 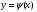 непрерывной СВ x (рис. 2.1). Будем считать, что существует взаимно однозначное преобразование непрерывной СВ x (рис. 2.1). Будем считать, что существует взаимно однозначное преобразование 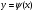 . Обратное преобразование обозначим . Обратное преобразование обозначим  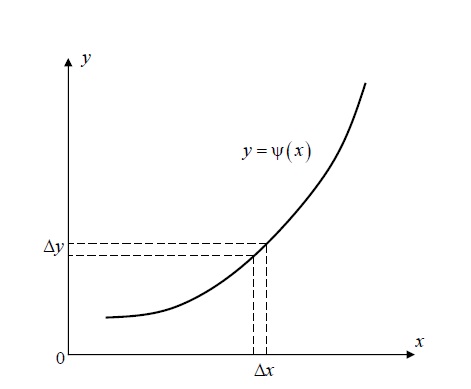 Рис. 1. Функциональное преобразование случайной величины Из рис. 1 видно, что всегда, когда СВ x попадает в интервал 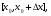 СВ y попадает в интервал СВ y попадает в интервал 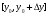 . Поэтому выполняется равенство . Поэтому выполняется равенство 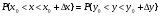 , откуда следует, что , откуда следует, что 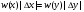 и при и при 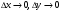 получаем соотношение получаем соотношение
Рассмотрим типичный пример получения СВ с заданным законом распределения из СВ с равномерным распределением. Пусть задана СВ x с равномерным законом распределения w(x)=1, x∈[0, 1], необходимо получить случайное число y с заданным законом распределения w(y), которому соответствует некоторое нелинейное преобразование, например, 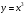 . Далее по формуле (1) получаем плотность вероятности . Далее по формуле (1) получаем плотность вероятности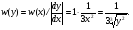 Теперь решим обратную задачу: найдем вид преобразования ψ(x) по заданной плотности распределения 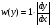 , y = ψ(x) . Для этого проинтегрируем левую и правую части (1) , y = ψ(x) . Для этого проинтегрируем левую и правую части (1)
откуда находим функцию распределения F ( y), тогда СВ y можно найти с помощью преобразования y = ψ(x). Описанный выше метод моделирования называется методом обратных функций. Для моделирования СВ с заданной функцией распределения необходимо осуществить нелинейное преобразование вида
Формула (3) означает решение уравнения
где 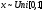 означает, что СВ x имеет равномерное распределение на отрезке [0, 1]. означает, что СВ x имеет равномерное распределение на отрезке [0, 1].Комбинируя формулы (2) и (3), можно по реализации СВ x с произвольной функцией распределения моделировать величины с требуемойфункцией распределения F(y). Моделирующий алгоритм дает суперпозициянелинейных преобразований (2) и (3): 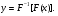 Получим с помощью метода обратных функций моделирующие алгоритмы для ряда распределений, используемых при моделировании случайных процессов и полей. Рассмотрим СВ с рэлеевским законом распределения. В этом случае плотность распределения вероятностей (ПРВ), функция распределения, среднее значение и дисперсия имеют соответственно вид: 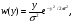 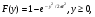 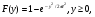 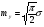 , ,  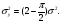 где σ — параметр рэлеевского распределения. При этом СВ y можно получить решая уравнение (4), откуда получаем:
где x - равномерно распределенная в интервале [0, 1] СВ (переход от ln(1− x) к ln x в последней формуле основан на том, что СВ 1− x и x имеют здесь одинаковые законы распределения). Аналогично, для получения СВ, описывающей интервалы времени между соседними заявками, поступающими на вход телекоммуникационной системы и имеющей показательный закон распределения 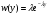 , , 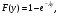 y ≥ 0 , y ≥ 0 ,решая уравнение F ( y) = x , т.е. 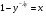 , находим обратную функцию , находим обратную функцию 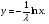 Таким образом, показательную СВ y можно сформировать из равномерной СВ x с помощью функционального преобразования Таким образом, показательную СВ y можно сформировать из равномерной СВ x с помощью функционального преобразования 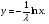 Путём преобразований
можно сформировать СВ, распределенные соответственно по закону арксинуса 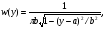  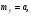 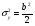 и закону Коши 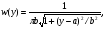 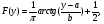 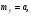 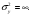 Используя свойство симметрии тригонометрических функций, нетрудно убедиться, что закон распределения СВ у, формируемых согласно алгоритмам (6), не изменится, если аргумент π(x −1/ 2) у тригонометрических функций заменить аргументом 2 π x . Рассмотрим СВ y , имеющую ПРВ: 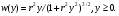 Соответствующая функция распределения 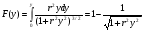 Уравнение (2) в данном случае примет вид 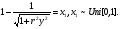 Находя отсюда y , получим 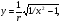 где 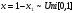 , r > 0. , r > 0.Рассмотрим моделирование СВ с плотностью
Интегрируя формулу (2.7), получим для функции распределения выражение 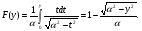 Отсюда получаем уравнение 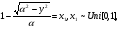 из которого следует моделирующий алгоритм 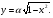 К сожалению, не всегда существуют элементарные преобразования для получения СВ с заданным законом распределения из равномерно распределенных СВ. В частности, у СВ с нормальным распределением функция, обратная функции распределения, не выражается через элементарные функции. В подобных случаях для формирования СВ с заданным распределением используются различные аппроксимации функции 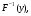 , а также другие подходы к решению задачи моделирования. , а также другие подходы к решению задачи моделирования.2.2. Метод суперпозиции Рассмотрим дискретную СВ y, принимающую n значений akс вероятностями p1,…,pn. Эта величина задается рядом распределения 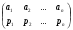 , , 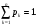 Обычно используют следующий алгоритм моделирования. Отрезок [0, 1] разбивают на n последовательных отрезков 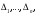 длины которых равны соответственно вероятностям длины которых равны соответственно вероятностям 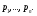 . Разыгрывается значение величины x∈[0,1] с равномерным распределением и далее принимается, . Разыгрывается значение величины x∈[0,1] с равномерным распределением и далее принимается, 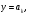 если если 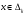 Этот алгоритм применим и для дискретных СВ, принимающих бесконечное множество значений. Для моделирования СВ с плотностью распределения вида
где 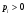 , , 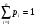 удобен метод суперпозиции. Моделирование осуществляется в два этапа. Сначала разыгрывается реализация дискретной СВ, принимающей значения 1, 2, . . ., n с вероятностями pk. После получения значения k , моделируется СВ с ПРВ удобен метод суперпозиции. Моделирование осуществляется в два этапа. Сначала разыгрывается реализация дискретной СВ, принимающей значения 1, 2, . . ., n с вероятностями pk. После получения значения k , моделируется СВ с ПРВ 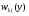 . Ее значение и принимается в качестве y . . Ее значение и принимается в качестве y .Модели вида (8) называются смесями распределений 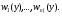 Описанный алгоритм по существу воспроизводит реальный физический механизм появления смесей распределений. Сумма в формуле (8) может содержать большое число слагаемых. Описанный алгоритм по существу воспроизводит реальный физический механизм появления смесей распределений. Сумма в формуле (8) может содержать большое число слагаемых. Рассмотрим пример применения метода суперпозиции. Пусть требуется промоделировать СВ с ПРВ вида 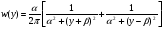 Лекция 5. 2.3. Некоторые специальные методы моделирования случайных величин Для моделирования СВ с заданным законом распределения можно использовать и другие свойства преобразований случайных чисел. Например, путем суммирования большого числа (12) случайных чисел xiс равномерным законом распределения в интервале (0, 1) можно получить СВy , ПРВ которой близка к нормальной ПРВ N (0, 1): 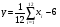 Известно также, что распределение произведения двух независимых СВ, одна из которых имеет рэлеевское распределение, а другая распределена по закону арксинуса (2.6) с нулевым средним значением и дисперсией, равной 1/2, является нормальным. Это позволяет формировать нормальную СВ путем следующего преобразования системы двух независимых равномерно распределенных в интервале (0, 1) случайных чисел x1 иx2:
Параметры получаемой этим способом нормальной СВ будут (0, σ2 ). Из этихже чисел можно получить еще одну нормальную СВ 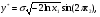 некоррелированную (а значит и независимую) с СВy . Для моделирования СВ с некоторыми законами распределения иногда удобно использовать преобразования нормально распределенных случайных чисел. Например, СВ с рэлеевским и показательным законами распределения можно получить путем преобразования системы двух независимых нормальных случайных чисел x1 иx2 спараметрами(0, σ2 ) в виде
соответственно. При этом для рэлеевского распределения параметр σ будетсовпадать спараметром σ исходного нормального распределения, а дляпоказательного распределения параметр λ связан с параметром σ исходногонормального распределения соотношением λ= 0.5σ2. Алгоритмы 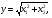 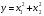 основаны на известных свойствахпреобразований нормальных СВ. Немного изменив эти алгоритмы, можномоделировать СВ с другими распространенными законами распределения. основаны на известных свойствахпреобразований нормальных СВ. Немного изменив эти алгоритмы, можномоделировать СВ с другими распространенными законами распределения.Полагая
получим соответственно СВ с законом распределения Райса 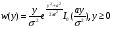 и СВ с законом распределения χ2 с m степенями свободы 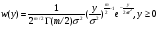 где I0(x)- модифицированная функция Бесселя нулевого порядка; Г(х)-гамма-функция. 2.3.1. Метод Неймана Для моделирования СВ, возможные значения которых не выходят запределы некоторого ограниченного интервала (a, b), а также СВ, законраспределения которых можно аппроксимировать усеченными, достаточноуниверсальным является метод Неймана, состоящий в следующем. С помощью датчика равномерно распределённых в интервале (0, 1) случайных чисел независимо выбираются пары чисел 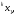 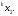 Из нихформируются преобразованные пары Из нихформируются преобразованные пары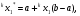 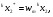 где (a, b) - интервал возможных значений СВy с заданной ПРВ w(y); 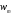 -максимальное значение ПРВ w(y). В качестве реализации СВ берется число -максимальное значение ПРВ w(y). В качестве реализации СВ берется число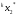 из тех пар ( из тех пар (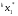 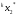 ), для которых выполняется неравенство ), для которых выполняется неравенство 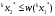 . .Пары, не удовлетворяющие этому неравенству, отбрасываются. Можнолегко убедиться в справедливости такого метода моделирования СВ.Действительно, пары случайных чисел( 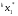 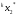 ),можно рассматривать каккоординаты случайных точек плоскости, равномерно распределенных вдольосей y и w(y) внутри прямоугольника aa'b'b(рис. 2). ),можно рассматривать каккоординаты случайных точек плоскости, равномерно распределенных вдольосей y и w(y) внутри прямоугольника aa'b'b(рис. 2).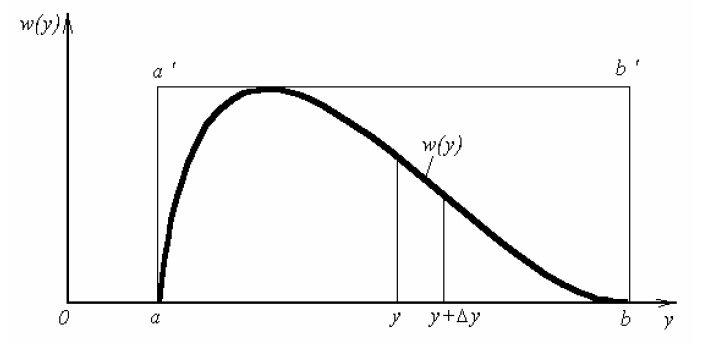 Рис. 2.2. Усеченная кривая плотности вероятности Пары( 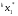 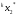 ), удовлетворяющие условию неравенства, представляютсобой координатыслучайных точек плоскости, равномерно распределенныхвдоль осей y и w( y) внутри тойчасти прямоугольника aa'b'b, котораярасположена под кривой w( y). Вероятность того, чтослучайная точкаплоскости, находящаяся под кривой w( y), окажется в элементарной полосес основанием ( y, y + Δy) пропорциональна w( y), а вероятность попаданияточки под кривую w( y) по условию равна единице, что и требуется. ), удовлетворяющие условию неравенства, представляютсобой координатыслучайных точек плоскости, равномерно распределенныхвдоль осей y и w( y) внутри тойчасти прямоугольника aa'b'b, котораярасположена под кривой w( y). Вероятность того, чтослучайная точкаплоскости, находящаяся под кривой w( y), окажется в элементарной полосес основанием ( y, y + Δy) пропорциональна w( y), а вероятность попаданияточки под кривую w( y) по условию равна единице, что и требуется.3.2. Метод кусочной аппроксимации Существуют различные приближенные приемы моделирования СВ:численноерешение уравнения x = F (y) относительно y при использованииметода нелинейного преобразования, обратного функции распределения;замена непрерывных распределений соответствующими дискретнымираспределениями, для которых можно указать достаточно простыемоделирующие алгоритмы и другие приёмы. Среди них универсальным инаиболее простым является метод кусочной аппроксимации. Сущность этого метода состоит в следующем. Пусть требуется получитьСВy с функцией плотности w( y). Предположим, что область возможныхзначений СВy ограничена интервалом (a, b) (неограниченное распределениеможно приближенно заменить ограниченным). Разобьем интервал (a, b) на nдостаточно малых интервалов (am,am+1), m=0,...,n−1,a0 =a,an=b, так, чтобы распределение заданной СВ в пределах этих интервалов можно былодовольно точно аппроксимировать каким-нибудь простым распределением(рис. 3), например, равномерным, трапецеидальным и т. д. В дальнейшем рассмотрим кусочную аппроксимацию равномерным распределением. 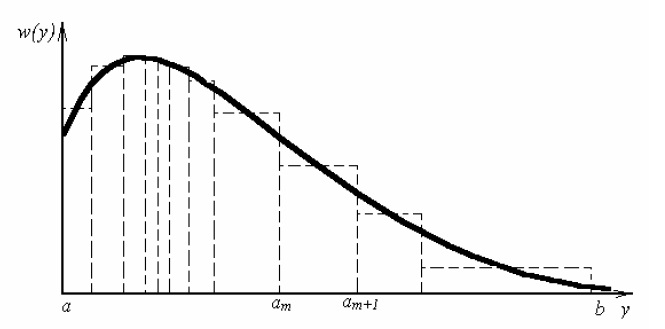 Пусть Pm - вероятность попадания СВy в каждый из интервалов (am,am+1). Получатьреализации величины y с кусочно-равномерным распределением можно, очевидно, в соответствии со следующей схемой преобразования случайных чисел: 1) случайным образом с вероятностью Pmвыбирается интервал (am,am+1); 2) формируется реализация 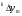 СВ,равномерно распределенной в интервале СВ,равномерно распределенной в интервале 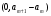 ; 3) искомаяреализация ; 3) искомаяреализация 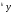 получается по формуле получается по формуле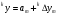 Случайный выбор интервала (am,am+1) с вероятностью Pmозначает, по существу, моделирование дискретной СВ, принимающей n значений am, m = 0, . . . , n −1, x0 =0, xn =, с вероятностью Pmкаждое, что можно сделать достаточно просто. Интервал (0, 1) разбивается на n интервалов (xm,xm+1), m = 0, . . . , n −1, x0 =0, xn =1, длиной (xm+1−xm)=Pmкаждый. Из датчика случайных, равномерно распределенных в интервале (0, 1) чисел выбирается некоторая реализация 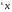 . Путем последовательного сравнения . Путем последовательного сравнения 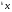 с xmопределяется тот интервал (xm,xm+1), в котором находится с xmопределяется тот интервал (xm,xm+1), в котором находится 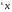 . . B основу этого процесса положен очевидный факт: вероятность попаданияравномерно распределенной в интервале (0, 1) СВ в некоторый подынтервал(xm,xm+1)равна длине этого подынтервала. Рассмотренный выше процесспредставляет интерес не только как составной элемент метода кусочнойаппроксимации, он широко используется в качестве алгоритма длямоделирования дискретных СВ и случайных событий. Для моделирования СВ методом кусочной аппроксимации наиболее удобно при машиннойреализации выбирать вероятности попадания во все интервалы (am,am+1)одинаковыми Pm=1/n,ачислоnтаким,чтоn=2N,гдеN- целое число, меньше или равное количествудвоичных разрядов чисел,вырабатываемых датчиком случайных чисел. В этом случае величины amдолжны быть выбраны таким образом, чтобы выполнялось равенство 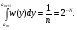 При равенстве вероятностей Pm для случайного выбора индекса m можноиспользовать первые N разрядов числа, извлекаемого из датчика равномернораспределенных случайных чисел. Используя рассмотренный прием, приходим к следующему способупреобразования равномерно распределенных случайных чисел в случайныечисла с заданным законом распределения. Из датчика равномернораспределенных в интервале (0, 1) случайных чисел извлекается парареализаций 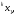 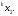 Первые Первые 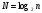 разрядов числа разрядов числа 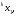 используются длянахождения адресов ячеек, в которых хранятся величины am,am+1, a затем поформуле используются длянахождения адресов ячеек, в которых хранятся величины am,am+1, a затем поформуле 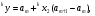 получается реализация получается реализация 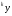 СВy с заданнымзаконом распределения. Такой алгоритм является довольно экономичным поколичеству требуемых операций, которое не зависит от числа n , т. е. не зависитот точностикусочной аппроксимации. Однако с увеличением точностиаппроксимации возрастает количество ячеек памяти, требуемое для хранениявеличин am, m = 0,… , n , что является недостатком рассмотренного метода прибольших значениях n . СВy с заданнымзаконом распределения. Такой алгоритм является довольно экономичным поколичеству требуемых операций, которое не зависит от числа n , т. е. не зависитот точностикусочной аппроксимации. Однако с увеличением точностиаппроксимации возрастает количество ячеек памяти, требуемое для хранениявеличин am, m = 0,… , n , что является недостатком рассмотренного метода прибольших значениях n .2.4. Моделирование векторных случайных величин Рассмотрим моделирование непрерывной векторной СВ 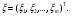 Ее полное описание задается совместной ПРВ Ее полное описание задается совместной ПРВ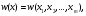 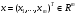 , где T – символтранспонирования. , где T – символтранспонирования.Стандартный метод моделирования векторных СВ основан на представлении w(x) в виде произведения
частной (маргинальной) ПРВ величины ξ1и условных ПРВ ξkпри условии,что 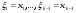 . Из формулы (17) следует, что вектор ξ, можетмоделироваться покомпонентно: сначала величина ξ1с ПРВ . Из формулы (17) следует, что вектор ξ, можетмоделироваться покомпонентно: сначала величина ξ1с ПРВ 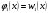 ,далее - ξ2по ПРВ ,далее - ξ2по ПРВ 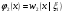 , потом - ξ3как величина с ПРВ , потом - ξ3как величина с ПРВ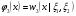 и т. д. Последней моделируется m-я компонента ξm,имеющая ПРВ и т. д. Последней моделируется m-я компонента ξm,имеющая ПРВ 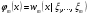 . Стандартныйметод требуетопределенной вычислительной работы, связанной с нахождением условных ичастных ПРВкомпонент. После вычисления ПРВ каждая компонентамоделируется как скалярная величина методами, изложенными выше. . Стандартныйметод требуетопределенной вычислительной работы, связанной с нахождением условных ичастных ПРВкомпонент. После вычисления ПРВ каждая компонентамоделируется как скалярная величина методами, изложенными выше.Рассмотрим подробнее процесс моделирования многомерногонормального распределения. Случайный вектор 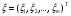 имеетневырожденное m-мерное нормальное распределение, если его ПРВ имеет вид имеетневырожденное m-мерное нормальное распределение, если его ПРВ имеет вид
где µµ1,...,µm)T - математическое ожидание ξ; R=[ρij]- заданная симметрическая положительно определенная m× m -матрицаx-µTR1x-µ- квадратичная форма переменных x− µ с матрицей BR1. Матрица 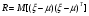 является ковариационной матрицей вектора ξ; обратная ей матрица B часто называется матрицей точности. Распределение (2.18) полностью описывается двумя параметрами: вектором µ и матрицей R. Далее используется краткое обозначение ξ N(µ, R). является ковариационной матрицей вектора ξ; обратная ей матрица B часто называется матрицей точности. Распределение (2.18) полностью описывается двумя параметрами: вектором µ и матрицей R. Далее используется краткое обозначение ξ N(µ, R). Если математическое ожидание равно нулю, а корреляционная матрица R равна единичной матрице I, т. е. ξ N(0,I, то распределение называется стандартным нормальным распределением. Стандартное распределение легко моделируется. Для этого нужно положить все компоненты ξ равными независимым реализациям СВξ N(0,1 ). В общем случае распределение (18) моделируется с помощью линейного преобразования xAxµ,xN0,I. Здесь m× m -матрица A=[aij] определяется разложением ковариационной матрицы R в произведение двух треугольных матриц
В уравнении (19) будем считать A нижней треугольной матрицей: 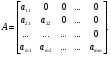 В этом случае явный вид коэффициентов ij a определяют следующие уравнения: 1 1 a111,ak1k1a1,k2,...,m, (20) l k1 akjaij a akl j1 ,l2,...,k1, (21) ll 2 k1 akkkk akj.(22) j1 После определения a11 вычисление элементов A осуществляется пo строкам: сначала по формуле (20) вычисляется первый элемент ak1k-й строки, далее по формуле (21) находятся последующие элементы ak2,...,ak,k1. Диагональный элемент вычисляется с помощью уравнения (22). После вычисления диагонального элемента осуществляется переход на следующую, (k+1)-юстроку. Плохая обусловленность (вырожденность) матрицы A требует проверки на каждой строке условия akk*,k2,...,m, означающего линейную зависимость k-й компоненты вектора ξ. Здесь ε* - малое число. Если это условие выполняется, то нужно положить akk0, длина k-й строки L(k) совпадает с длиной предыдущей. Индекс l принимает значения 2,3,...,L(k) его предельное значение L (k) - переменно. Число L (k)является счетчиком числа линейно независимых элементов последовательности ,...,. Присвоение L(k)последующего значения Lk1)Lk1осуществляется лишь при условии akk*. После расчета последней m-й строки значение L(m) равно рангу матрицы R. 2.5. Заключительные замечания Существует довольно большое количество методов моделирования СВ. В данном разделе были изложены некоторые из них. При этом преследовалась цель привести примеры алгоритмов для моделирования СВ с распространенными законами распределения. Рассмотрим краткую сравнительную характеристику различных методов моделирования СВ и некоторые рекомендации для выбора того или иного подхода для решения конкретных задач. В тех случаях, когда требуется высокая точность воспроизведения законов распределения СВ, целесообразно использовать методы моделирования, не обладающие методической погрешностью. К ним относятся описанные в пп. 2.2, 2.3 алгоритмы получения СВ (5), (6), (15), (16). Погрешностью таких алгоритмов часто можно пренебречь, так как она определяется лишь погрешностью выполнения на ЭВМ необходимых нелинейных преобразований и отклонением закона распределения исходных случайных чисел от равномерного. Примером систем, при моделировании которых может потребоваться высокая точность воспроизведения законов распределения СВ, являются системы приёма цифровых радиосигналов с низкой вероятностью ошибки(порядка10–4…10–6). Другим достоинством указанных алгоритмов является простота подготовительной работы, так как преобразования равномерного закона в требуемый закон распределения даются в виде готовых аналитических зависимостей. Такие алгоритмы, кроме того, позволяют легко изменять форму закона распределения в процессе моделирования СВ. Например, изменение ПРВ семейства Райса, сводится к изменению по соответствующему закону только параметров a и σ в алгоритме (16). Основным недостатком этих алгоритмов является сравнительно низкое быстродействие, так как выполнение на ЭВМ нелинейных преобразований часто требует довольно большого количества элементарных операций. B задачах, не предъявляющих высоких требований к качеству СВ, для сокращения количества элементарных операций рекомендуется использовать более экономичные приближённые методы (п. 2.3). Лекция 6 |