Физика лекции Юнусова (1). Минимальный курс физики. Составлен доц. Юнусовым Н. Б

• Название: Минимальный курс физики. Составлен доц. Юнусовым Н. Б
• Дата: 18.04.2023
• Размер: 3.72 Mb.
• Имя файла: Физика лекции Юнусова (1).doc
• Тип: Закон; #1071701
• страница: 2 из 19

Закон сохранения механической энер­гии: в инерциальной системе отсчета полная механическая энергия замкнутой системы час­тиц, в которой действуют только консервативные силы, сохраня­ется:

E = Е_КИН+ Е_ПОТ= const.

Сохраняется именно полная механическая энергия, в то время как кинетическая и потенци­альная энергии по отдельности могут меняться. В основе закона сохранения механической энергии лежит свойство однородности времени, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора начала отсчета времени. Например, потенциальная энергия поднятого на некоторую высоту тела не меняется с течением времени. Если бы это было не так, то можно было бы поднять тело, дождаться момента, когда его энергия увеличится, и заставить тело совершить работу. Мы получили бы вечный двигатель, работающий за счет разности энергий: возросшей с течением времени и затраченной на подъем тела.

Закон сохранения импульса: в инерциаль­ной системе отсчета импульс замкнутой системы частиц остается постоянным как по величи­не, так и по направлению,т.е. .

Действительно, из уравнения движения следует для замкнутой системы ( ), что импульс системы остается постоянным.

При этом импульсы отдельных частей систе­мы могут меняться. У незамкнутой системы может сохраняться не сам импульс, а его про­екция на то направление, по которому сумма проекций действующих сил равна нулю. В основе закона сохранения импульса лежит свойство однородности пространства, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора положения начала координат. Если бы пространство было неоднородным, т.е. точки пространства были бы неэквивалентны, то при движении свободного тела эта неэквивалентность проявилась бы в изменении импульса (появлении ускорения).

С помощью законов сохранения можно, не решая уравнений динамики, сделать во многих случаях ряд заключений о свойствах процессов, не вникая в их детальное рассмотрение.

Законы сохранения представляют собой об­щие фундаментальные принципы и отражают свойства пространства и времени.
1.4. МЕХАНИКА ТВЕРДОГО ТЕЛА.
Кинетическая энергия вращения. Момент инерции материальной точки и тела относительно неподвижной оси.

Пусть материальная точка массой m движется вокруг некоторой оси по окружности радиуса r со скоростью υ. Тогда кинетическую энергию точки с учетом связи линейной и угловой скоростей υ=ω·r можно записать так:

, где величина J=m·r² называется моментом инерции материальной точки.

Моментом инерции тела относительно оси называется сумма моментов инерции эле­ментов (материальных точек), из которых состо­ит тело: .

Момент инерции сплошного тела определя­ют интегрированием по всему объему (по всем материальным точкам): .

Если тело имеет плотность ρ, то последнее равенство можно представить в виде:

, где учтено, что d т= ρ·dV.

Момент инерции сплошного цилиндра мас­сой ти радиуса основания R относительно оси, проходящей через центр масс цилиндра па­раллельно его образующей, рассчитанный по этой формуле, равен: .

Для сплошного шара массой ти радиуса Rмомент инерции относительно оси, проходящей через центр масс шара, равен: .

Момент инерции для стержня длиной ℓ и массой т относительно оси, проходящей через центр масс стержня перпендикулярно ему, : .

Момент инерции J тела характеризует, с одной стороны, инертные свойства тела при вращательном движе­нии, а с другой стороны, распределение вещества в пространстве относительно оси. Момент инерции, так же как и масса тела, является ад­дитивной величиной.

Если известен момент инерции J_oтела от­носительно оси, проходящей через центр масс тела, то можно найти его момент инер­ции относительно любой другой параллельной ей оси: J = J₀ + m·d², где d – расстояние между осями.

Последнее равенство выражает теорему Штейнера: момент инерции относительно любой оси вра­щения равен моменту инерции относительно параллельной оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния центра масс тела от оси вращения.

Из теоремы Штейнера очевидно, что всег­да J>J₀, т.е. минимальное значение момента инерции до­стигается для оси, проходящей через центр масс.

Единицей момента инерции в системе СИ служит 1 кг·м².

Если тело катится, то кинетическая энергия такого тела определяется поступательным движением тела как целого и вращением относительно движущейся оси:

.
Момент импульса. Момент силы.

Основной характеристикой вращательного движения точки является момент импульса. Моментом импульса (или угловым мо­ментом) материальной частицы относительно точкиО называется векторная величина , где – радиус-вектор, определяющий положе­ние частицы относительно точки О, –импульс частицы. Модуль этой величины равен L = r·p·sina. Вектор направлен перпендикулярно плос­кости, в которой лежат радиус-вектор и импульс так, что они ( , и ) образуют правовинтовую тройку, аналогичную тройке векторов _. Проекция вектора на произвольную ось Z , проходящую через точку О, называется момен­том импульса относительно этой оси: . С учетом того, что , можно записать для момента импульса . Если поставить вертикально детскую игрушку – юлу – и отпустить, то она падает. Если же ее предварительно раскрутить, то она уже не падает. Т.о., у вращающегося тела появляется новое свойство, которое и характеризует момент импульса .

Рассмотрим частицу, вращающуюся вокруг некоторой оси под действием силы , ле­жащей в плоскости, перпендикулярной оси вра­щения, и приложенной к частице в точке с радиус-вектором . Аналогично моменту импульса опреде­ляется и момент силы относительно точки О: и относительно осиZ: .

Вектор характеризует способность силы вращать частицу вокруг точки О. Поэтому момент силы называют также вращающим момен­том.

Единицей момента импульса в СИ является 1кг·м²/с, а момента силы 1 Н·м.
Динамика твердого тела

Пусть на материальную точку действует сила . Умножим векторно правую и левую части уравнения движения этой точки на радиус-вектор точки приложения силы: .

Так как и , то заменяя, получим основное урав­нение динамики вращательного движе­ния материальной точки: .

Это уравнение легко обобщить на твердое тело, если под и понимать суммарный момент импульсов частиц , из которых состоит тело, и суммарный момент сил, , действующих на эти частицы. Приведем различные формы записи этого уравнения при неизменном моменте инерции (J=const):

.

Формально все соотношения, описывающие динамику вращательного движения, можно по­лучить из соответствующих соотношений дина­мики поступательного движения материальной точки, если в последних заменить массу тела на момент инерции, силу – на момент силы, им­пульс точки – на момент импульса тела, а ли­нейные скорость и ускорение – на угловые ско­рость и ускорение.

Из основного уравнения динамики для вращательного движения для замкнутой системы ( ) следует закон сохранения момента импульса: в инерциальной системе отсчета момент им­пульса замкнутой системы частиц остается по­стоянным как по величине, так и по направле­нию,т.е. .

В основе закона сохранения момента импульса лежит свойство изотропности (равноправности всех направлений) пространства, которое проявляется в том, что физические свойства и законы движения замкнутой системы не зависят от выбора направлений осей координат инерциальных систем отсчета..
1.5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА.

В конце 19 века было показано, что классическая механика не применима к описанию движения тел с очень большими, близкими к скорости света, скоростями. Это позволяет делать теория, созданная А.Эйнштейном.

Специальная теория относительности (СТО) или по другому релятивистская динамика опирается на два постулата:

Первый постулат (принцип относительности): все законы физики имеют одинаковую форму во всех инерциальных системах отсчета (ИСО).

В 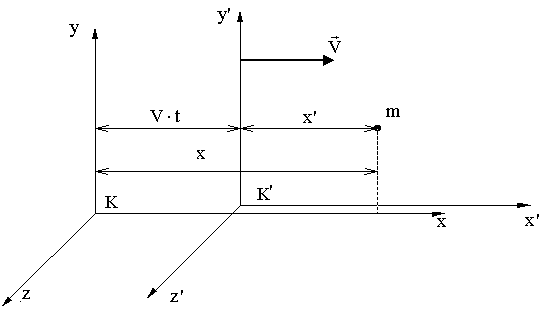торой постулат (постоянство скорости света): свет распространяется в пустом пространстве со скоростью с = 3·10⁸ м/с, не зави­сящей от скорости движения источника или наблюдателя.
Пусть система отсчета Kявляется неподвижной, а система K’ движется относи­тельно нее вдоль оси x со скоростью υ.

Уравнения преобразования координат и времени для т. m при переходе от одной ИСО к другой, полученные Лоренцем, имеют вид:


Следствия из преобразований Лоренца.

1. Сокращение длины. Пусть вдоль оси x’ в движущейся системе отсчетаK’ лежит стержень длины ℓ_o (это собственная длина или длина предмета (стержня) в той системе отсчета, в которой он покоится). Тогда ℓ – длина стержня относительно неподвижной системы отсчета K– равна :

Таким образом, движущийся предмет кажется наблюдателю более коротким, чем покоящий­ся. Сокращение происходит только в направле­нии относительного движения и становится за­метным лишь при υ, близкой к скорости света в вакууме с.

2. Замедление времени. ,

где Δt₀ – собственное время, т.е. промежу­ток времени в системе, где часы покоятся, Δt соответствует промежутку времени в системе, относительно которой часы движутся, причем Δt > Δt₀. Таким образом, движущиеся часы идут медленнее покоящихся.

3. Относительность одновременности. События, одновременные в одной ИСО, оказываются неодновременными по отношению к другой ИСО.

4. Релятивистские формулы преобразо­вания скоростей (закон сложения скоростей) получаются дифференцированием по времени преобразований Лоренца:

;

;

.

Здесь и_х , и_у , u_z , u’_x, u’_yи и'_г— проекции скорости движущейся частицы на оси неподвижной и по­движной систем отсчета, соответственно. Отсюда следует, что скорость света, равная u’_x = с относительно системы отсчета K’, и относительно Kбудет равнаи_х = с.

Физические величины, которые не меняются при переходе от одной инерциальной системы к другой, называются инвариантами теории относительности. К инвариантам, например, относятся скорость света в вакууме, масса и электрический заряд частицы, пространственно-временной интервал .

А. Эйнштейн показал, что закон природы – основное уравнение динамики – будет инвариантен к преобразованиям Лоренца, если импульс тела будет иметь вид: .

Из этой формулы видно, что тело, обладающее массой, не может двигаться со скоростью, большей или равной скорости света с . Из этой же формулы следует, что со скоростью света может двигаться, обладая конечным импульсом, только безмассовая частица (m=0). Это, например, фотон.

Основное уравнение динамики в СТО принимает, т.о., вид:

.

Если сила совершает работу, разгоняя тело от нулевой скорости до некоторой релятивистской скорости , то эта работа целиком идет на создание кинетической энергии, т.е.: . Вычисление интеграла приводит к выражению: .

Если истолковывать как полную энергию тела, то отсюда следует, что когда тело покоит­ся и его кинетическая энергия равна нулю, оно тем не менее обладает энергией т_·с². В соот­ветствии с этим т_·с²называют энергией покоя тела : Е₀ = m·c². Это знаменитая формула Эйнштейна, говорящая о том, что масса тела является не только мерой инертно­сти или мерой гравитационного действия, но и мерой энергосодержания тела. Используя выражения для импульса и энергии тела можно получить еще одно часто используемое выражение для полной энергии тела:

.

Согласно СТО, пространство и время являются относительными, зависят друг от друга, образуя единый 4-х мерный пространственно-временной континуум.

Несколько позже в общей теории относительности А. Эйнштейн показал, что на пространство и время влияет тяготение, а именно, вблизи очень массивных тел пространство искривляется, а время замедляется.

1.6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ

Д вижение, которое повторяется через равные промежутки времени, называется колебатель­ным. Промежуток времени T, по истечение кото­рого движение повторяется, называется перио­дом колебания. В моменты времени tи t + Т частица имеет одно и то же положение и одну и ту же скорость. Величина ν, обратная периоду, называется частотой: ν = 1/Т. Она определяет, сколько раз в секунду повто­ряется движение, и измеряется в герцах(Гц). Круговой (циклической) частотой называ­ется величина ω = 2πv.

Свободные (собственные) колебания – колебания, происходящие без внешних воздей­ствий за счет первоначально полученной телом энергии. Рассмотрим горизонтальный пружинный маятник жесткостью k и массой m, помещенный в среду с коэффициентом сопротивления r, на который вдоль оси х действует переменная внешняя сила F(t), изменяющаяся со временем, например, по гармоническому закону F(t) = F₀ ·cosΩt с некоторой частотой Ω .

Уравнение движения маятника:

(1), где сила упругости F_УПР пропорциональна смещению х, а сила трения (сопротивления) F_ТР среды – скорости υ=dx/dt. Перепишем (1) по другому:

(2),

где введены обозначения

Проанализируем уравнение (2).