|
|
Физика лекции Юнусова (1). Минимальный курс физики. Составлен доц. Юнусовым Н. Б
Свободные гармонические незатухающие колебания.
 Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид: Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид:
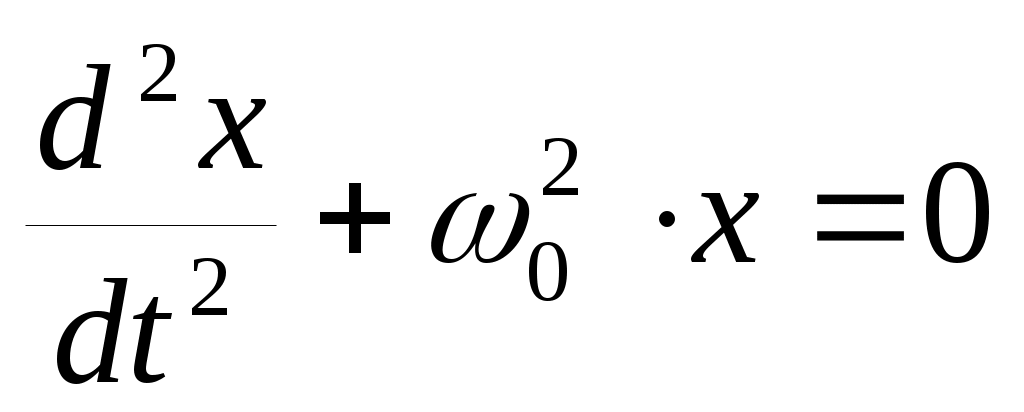 (3). (3).
Его решением является гармоническая функция: 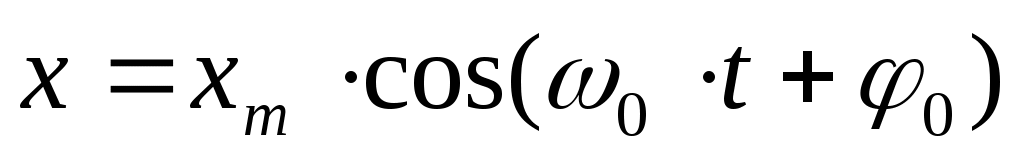 (4), (4),
в чем легко убедиться, подставив (4) в (3).
В (4) xm , ω0 и φ0 – постоянные величины. xm– амплитуда – величина, указывающая максимальное значение координаты х при отклонении от положения равновесия, ω0 – собственная частота, аргумент косинуса 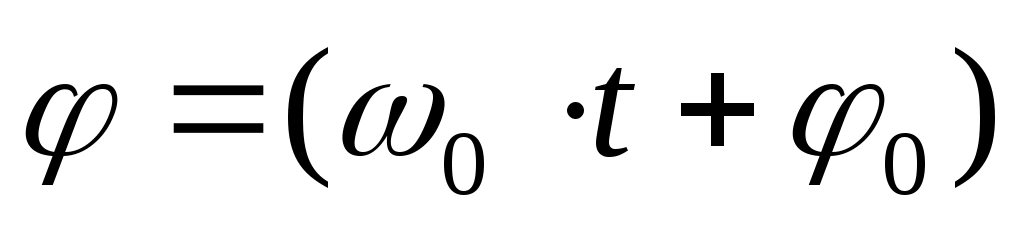 носит название фазы колебания; φ0 — начальная фаза колебания (в момент t= 0). носит название фазы колебания; φ0 — начальная фаза колебания (в момент t= 0).
Частота колебаний зависит только от свойств колеблющейся системы, но не от амплитуды, а амплитуда и начальная фаза колебаний определяются начальными условиями ее движения, выводящими систему из состояния покоя.
Скорость колеблющейся частицы равна: 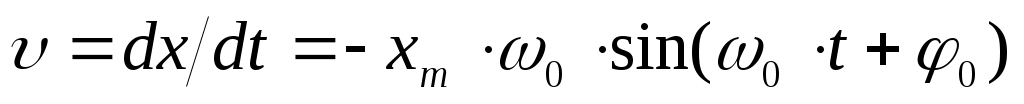 (5). (5).
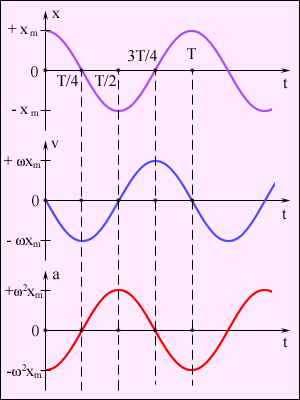
Ускорение частицы при таком движении: 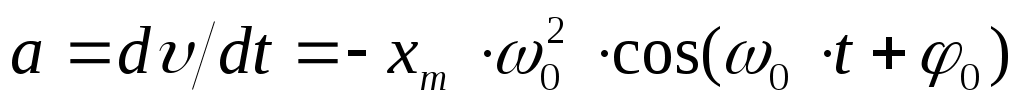 (6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0=0. (6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ0=0.
Складывая кинетическую энергию с потенциальной, найдем полную энергию частицы, колеблющейся под действием упругой силы:
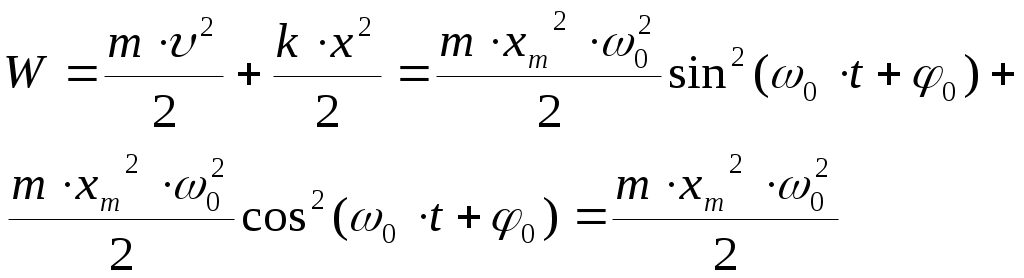 (7). (7).
Т.о., полная энергия пропорциональна квадрату амплитуды колебаний. Кинетическая и потенциальная энергии изменяются со временем, как sin2(ω0·t+φ0) и cos2(ω0·t+φ0) , так что когда одна из них увеличивается, другая – уменьшается, т.е. процесс колебаний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Средние за период колебания значения потенциальной и кинетической энергии одинаковы и равны W/2. Т.о., если на тело действует сила, пропорциональная величине смещения частицы х и направленная в сторону, противоположную этому смещению (таковы, например, упругая сила, F=– k·x , действующая на пружинный маятник, или сила тяжести, действующая на математический или физический маятники), то оно совершает т.н. гармонические колебания (движение совершается по закону синуса или косинуса).
Примечание: В механике обычно рассматривают колебания : – математического маятника с периодом 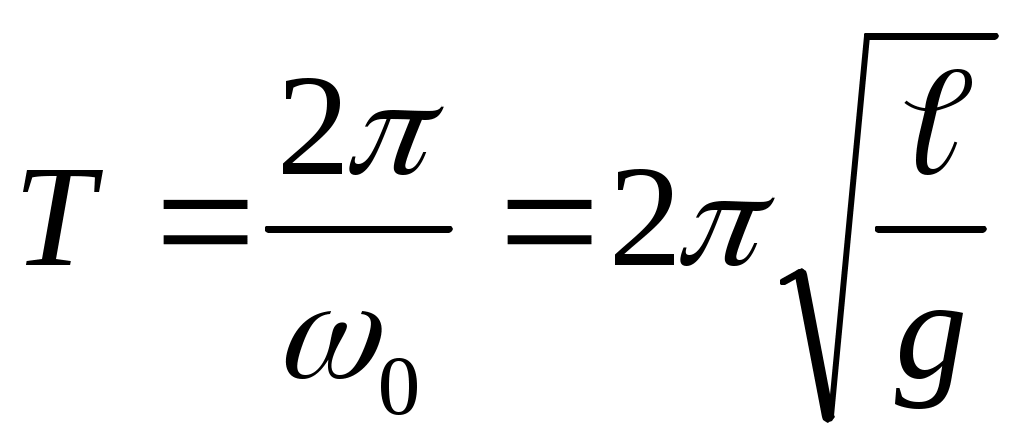 , где ℓ–длина маятника; , где ℓ–длина маятника;
– физического маятника с периодом 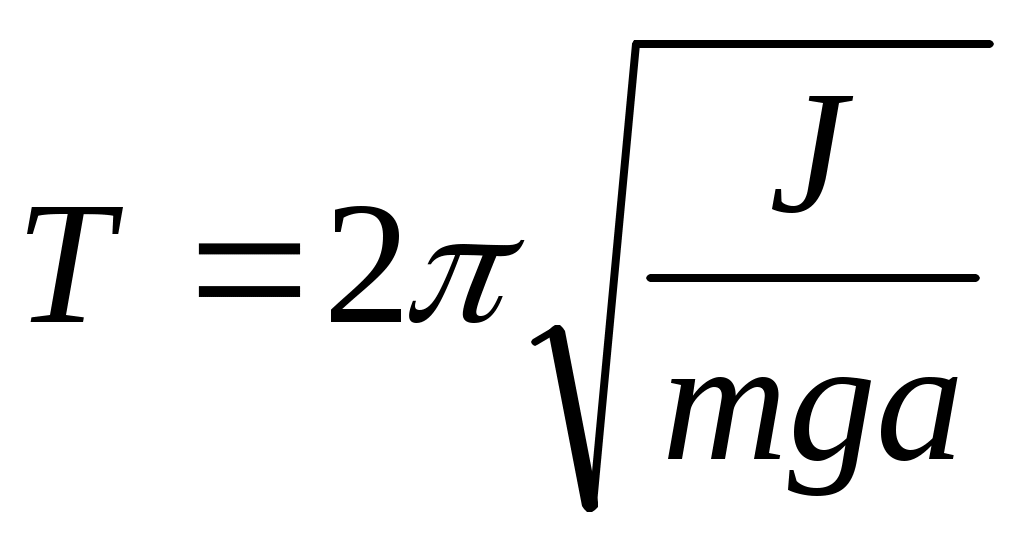 , где J–момент инерции маятника, a–расстояние от точки подвеса маятника до его центра масс; , где J–момент инерции маятника, a–расстояние от точки подвеса маятника до его центра масс;
– пружинного маятника с периодом 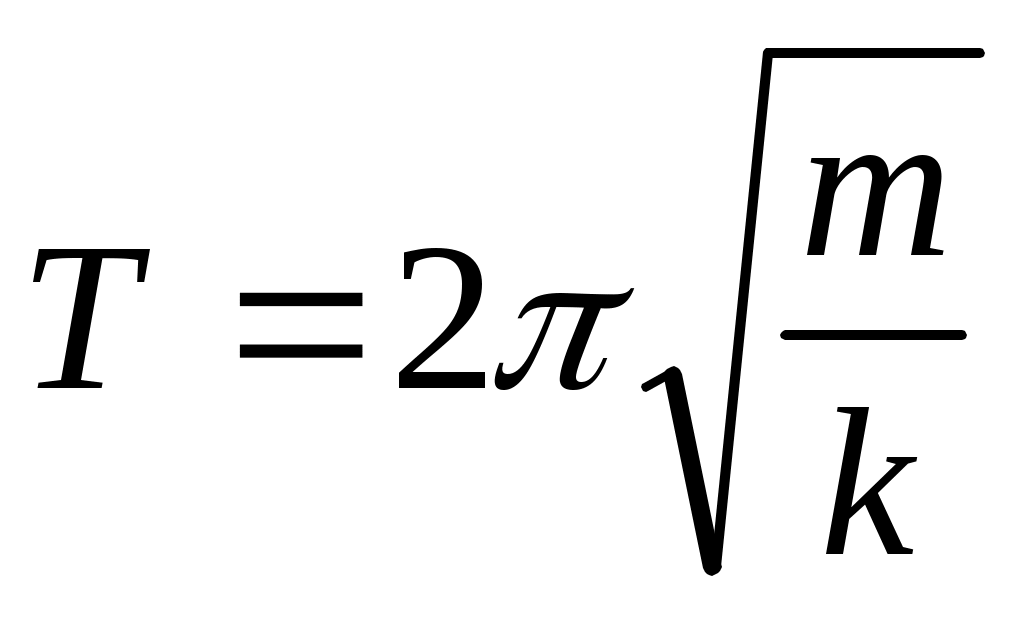 , где k–жесткость пружины. , где k–жесткость пружины.
2. Свободные затухающие колебания
При наличии силы трения (r ≠0) и отсутствии внешней периодической силы (F0 =0) уравнение движения имеет вид: 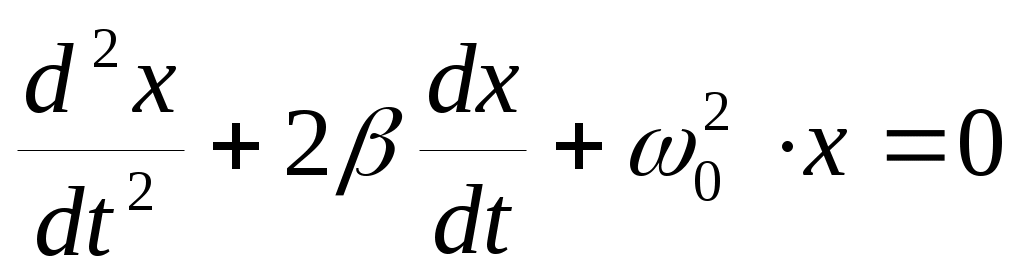 (8), (8),
г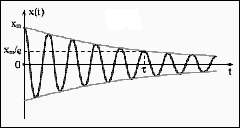
де β называется коэффициентом затухания колебаний. В случае слабого затухания (β – мало) решением такого дифференциального уравнения является функция : 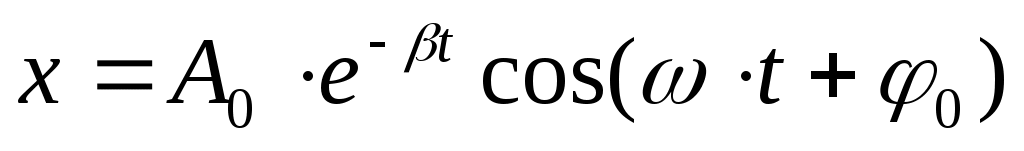 (9). В этом можно убедиться прямой подстановкой (9) в уравнение (8). (9). В этом можно убедиться прямой подстановкой (9) в уравнение (8). 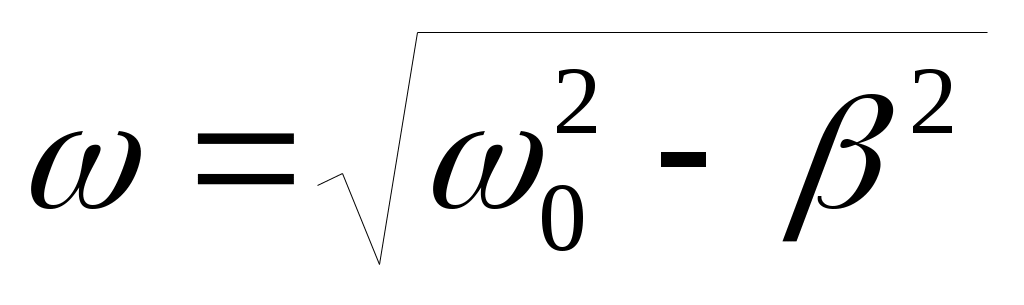 – частота колебаний системы с затуханием. A=A0·e-βt – амплитуда затухающих колебаний. – частота колебаний системы с затуханием. A=A0·e-βt – амплитуда затухающих колебаний.
Таким образом, амплитуда колебаний убывает по экспоненциальному закону. Вместе с амплитудой убывает также и энергия колебаний W, т.к. W
A2.
Степень убывания амплитуды определяется коэффициентом затухания β. Время τ=1/β, за которое амплитуда колебаний уменьшается в е=2.7183 раз, называют постоянной времени затухания колебаний.
Скорость уменьшения амплитуды за период характеризует величина θ, называемая логарифмическим декрементом затухания. По определению:
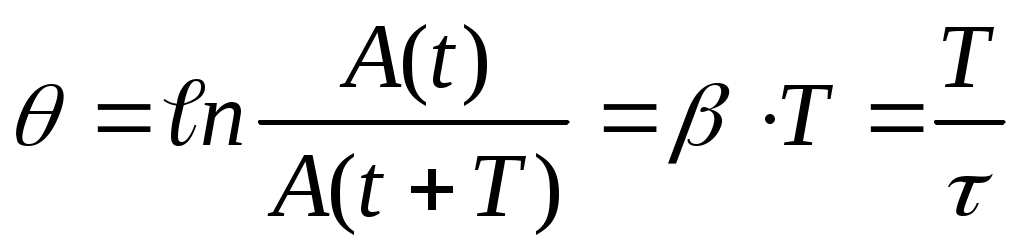 (10). (10).
Скорость убывания энергии в системе с затуханием характеризует добротность Q:
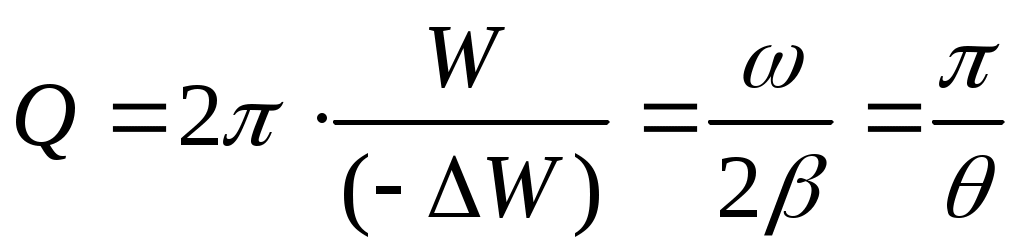 (11), (11),
где W – энергия, запасенная в системе, (–ΔW)– энергия, теряемая системой за период. Добротность показывает, во сколько раз энергия, запасенная в системе, больше энергии, теряемой за период. Добротность в (11) выражена через параметры системы и логарифмический декремент затухания θ, с учетом того, что W
A2.
В случае сильного затухания (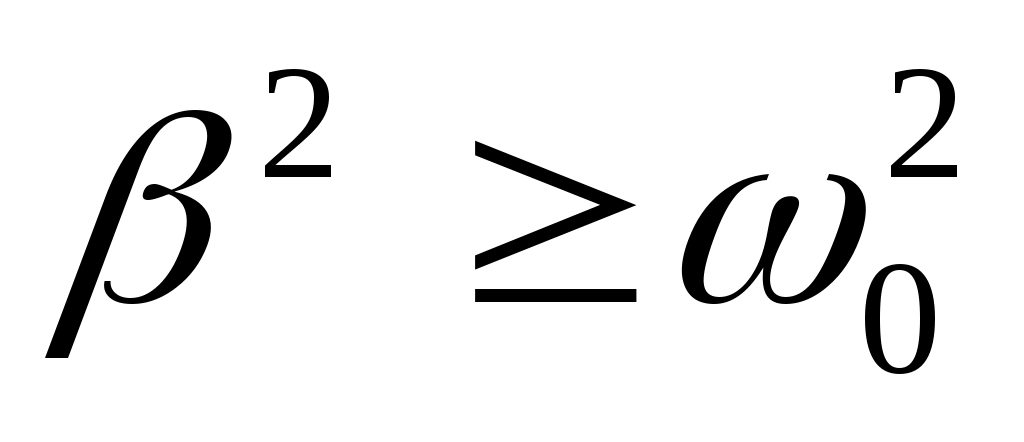 ) колебательный процесс не развивается: система, выведенная из состояния равновесия и предоставленная самой себе, просто медленно возвращается к нему. Это т.н. апериодический процесс. ) колебательный процесс не развивается: система, выведенная из состояния равновесия и предоставленная самой себе, просто медленно возвращается к нему. Это т.н. апериодический процесс.
3. Вынужденные колебания. Резонанс.
Для того чтобы возбудить в системе незатухающие колебания, необходимо компенсировать потери энергии, обусловленные трением (сопротивлением). Такая компенсация может производиться внешними по отношению к колебательной системе источниками энергии. Простейшим случаем является воздействие на систему переменной внешней силы F(t). Под влиянием этой силы в системе возникнут колебания, происходящие в такт с изменением силы; эти колебания называются вынужденными.
Дифференциальное уравнение вынужденных колебаний имеет вид (2):
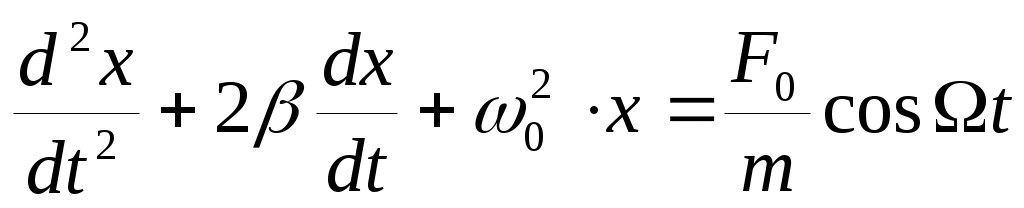 (12). (12).
Это уравнение является линейным неоднородным дифференциальным уравнением 2 порядка; его общее решение представляет собой сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения есть решение уравнения колебаний с затуханием, рассмотренное ранее. Рассмотрим частное решение неоднородного уравнения: x =A·cos(Ωt –φ ) (13), описывающее установившиеся колебания с частотой Ω вынуждающей силы.
Величины амплитуды Aи сдвига фазы φ по отношению к фазе вынуждающей силы зависят от соотношения между собственной частотой ω0 системы и Ω, а также от затухания, действующего в системе:
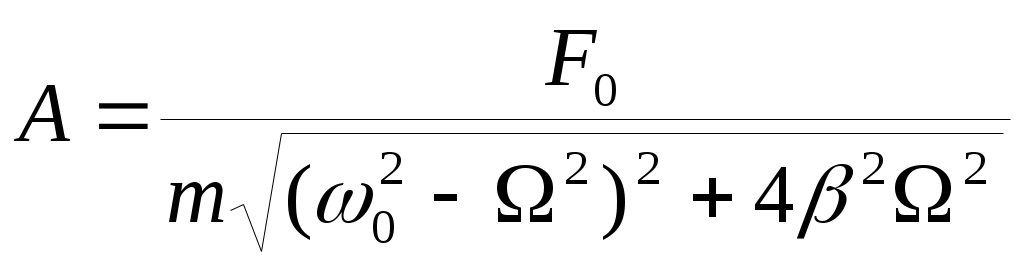 ; ; 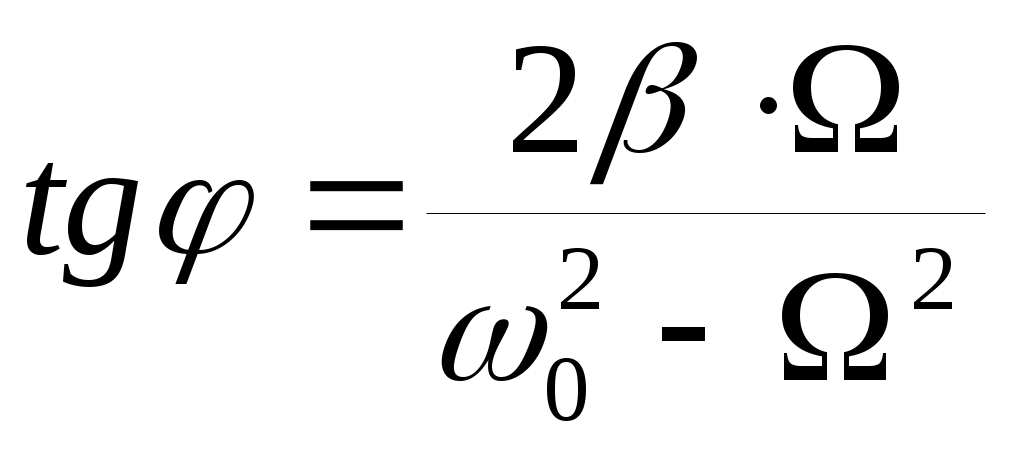 (14). (14).
П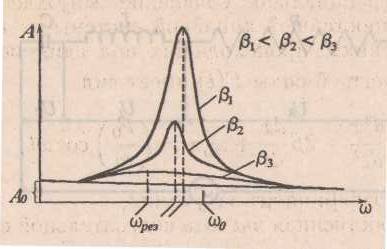 ри некоторой частоте Ω0вынуждающей силы амплитуда вынужденных колебаний достигает максимума. Это явление называется резонансом (резонансом смещения). На рис. изображены резонансные кривые для трех значений коэффициента затухания β. Частота ωрез = Ω0 называется резонансной частотой. Ее значение можно найти, исследовав на минимум подкоренное выражение для A в формуле (14): ри некоторой частоте Ω0вынуждающей силы амплитуда вынужденных колебаний достигает максимума. Это явление называется резонансом (резонансом смещения). На рис. изображены резонансные кривые для трех значений коэффициента затухания β. Частота ωрез = Ω0 называется резонансной частотой. Ее значение можно найти, исследовав на минимум подкоренное выражение для A в формуле (14): 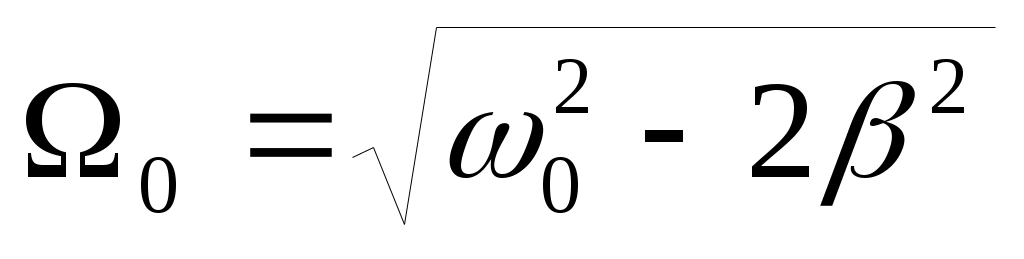 (15). (15).
Амплитуда при резонансе получается подстановкой Ω0 в выражение для амплитуды:
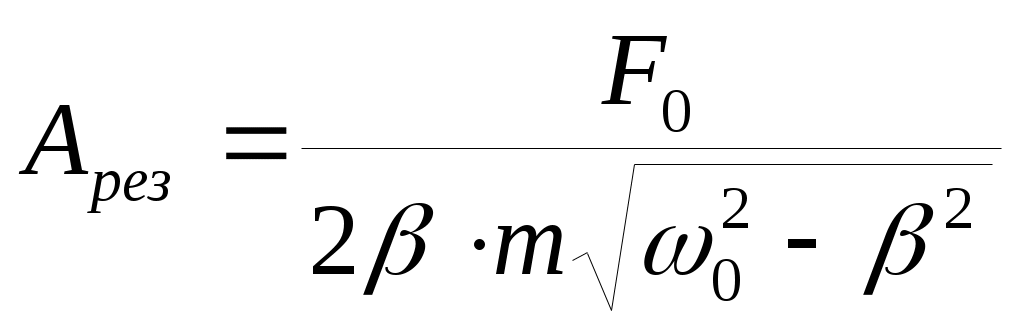 (16). (16).
1.7. МЕХАНИЧЕСКИЕ ВОЛНЫ.
Явление распространения колебаний в пространстве называется волновым движением или волной.
Уравнение волны выражает зависимость смещения Ψ колеблющейся точки, участвующей в волновом процессе, от ее координаты х и времени t.
Волна называется продольной, если колебания частиц происходят вдоль линии распространения волны; если колебания частиц перпендикулярны к направлению распространения волны, то волна называется поперечной.
Геометрическое место точек, до которых к некоторому моменту времени дошло колебание, называется фронтом волны. Можно также в среде выделить геометрическое место точек, колеблющихся в одинаковых фазах. Эта совокупность точек образует поверхность одинаковых фаз или волновую поверхность. Форма фронта волны определяет тип волн, например, у сферической волны фронт представляет собой сферу.
Скорость распространения волны есть скорость распространения данной фазы (волновой поверхности). Ее называют фазовой скоростью υ волны.
Расстояние, на которое определенная фаза колебания распространяется за один период Т колебания, называется длиной волны λ =υ·T.
Простейшим видом волн является плоская волна. Колебания частиц среды в ней происходят в плоскостях, перпендикулярных к направлению распространения. Если колебания в каждой точке следуют гармоническому закону и происходят с одной частотой, то волна называется гармонической и монохроматической.
Уравнение плоской волны, распространяющейся в положительном направлении оси х, имеет вид: 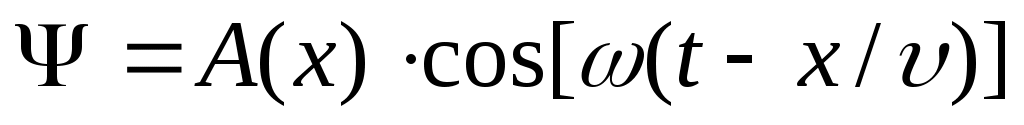 (17), (17),
где А(х) = A0·e-rx – амплитуда колебаний точек среды, расположенных на расстоянии x от источника колебаний (в среде без затухания А=А0= const). Так как ω=2π/T, то: 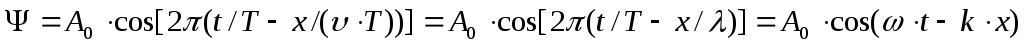 (18). (18).
Здесь k=2π/λ=2π/(υ·T)=2πν/υ=ω/υназывается волновым числом и является модулем волнового вектора 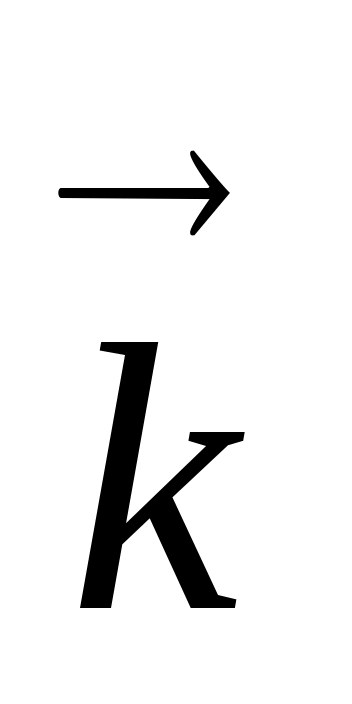 , указывающего направление распространения волны. , указывающего направление распространения волны.
Уравнение волны в виде (18) – одно из возможных решений общего дифференциального уравнения, описывающего распространение возмущения в среде. Это общее уравнение называется волновым уравнением. Его можно получить, взяв от функции Ψ вторые производные по х и t,: 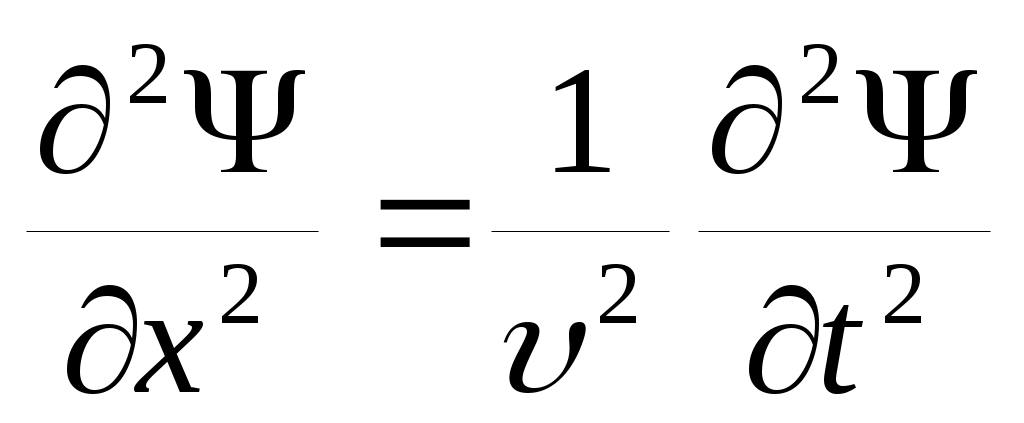 (19), (19),
где учтено, что в данном случае производные являются частными и сделана замена 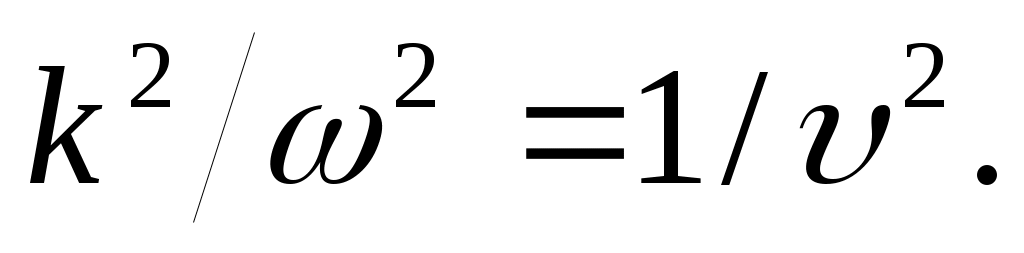 Выражение (19) справедливо для волн любой природы. Выражение (19) справедливо для волн любой природы.
Вещество вместе с волной не переносится. Частицы вещества только колеблются каждая около своего положения равновесия. Колебания передаются вдоль направления распространения волны, вместе с ними передается и их энергия. Для описания этого процесса вводят вектор плотности потока энергии (вектор Умова) 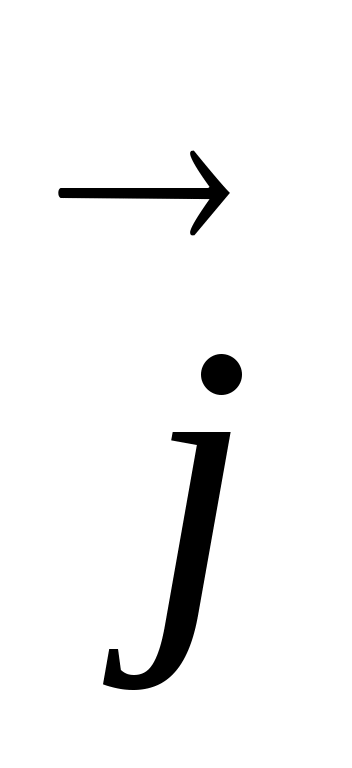 , который направлен в сторону распространения волны, а его модуль равен энергии, переносимой волной через единицу площади за единицу времени. , который направлен в сторону распространения волны, а его модуль равен энергии, переносимой волной через единицу площади за единицу времени.
Выделим на фронте плоской волны (рис.) единичную площадку S. Через единицу времени фронт сместится на расстояние, равное скорости распространения волны υ и займет положение S’. Если в единице объема содержится энергия w (плотность энергии), то за единицу времени через сечение S’= 1 пройдет вся энергия, заключенная в объеме между сечениями Sи S’ , т. е. w·υ. Это и есть вектор Умова, если записать в векторной форме: 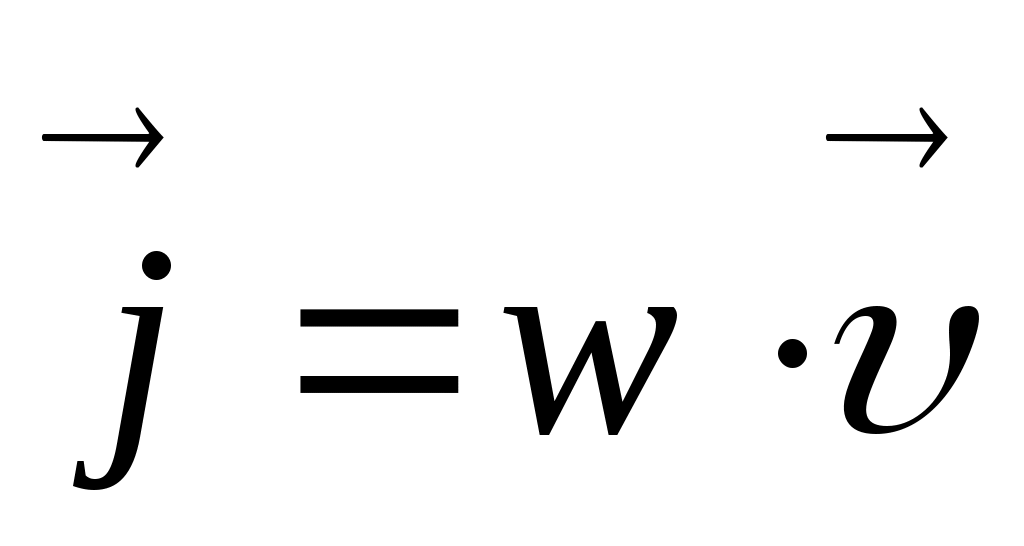 . Он измеряется в Дж/(с·м2) или, что то же самое, в Вт/м2. Эта формула справедлива не только для механических волн, но и для волн любой природы, например электромагнитных. . Он измеряется в Дж/(с·м2) или, что то же самое, в Вт/м2. Эта формула справедлива не только для механических волн, но и для волн любой природы, например электромагнитных.
|
|
|
 Скачать 3.72 Mb.
Скачать 3.72 Mb. Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид:
Маятник в отсутствие силы трения (r =0) и внешней силы ( F0=0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид: 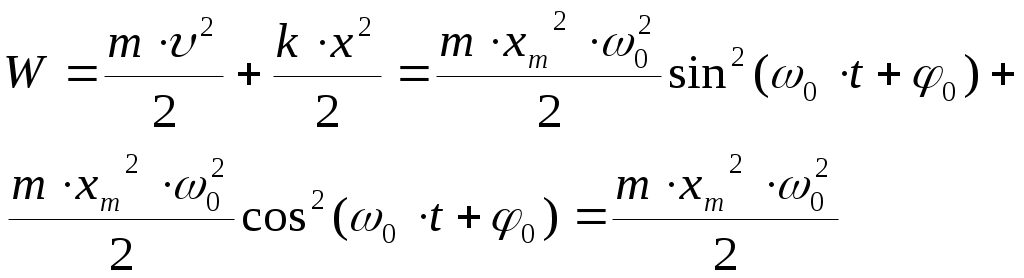 (7).
(7).

 ри некоторой частоте Ω
ри некоторой частоте Ω