Вариант 17 надо выполнить. 1-2-3-4 РГР247. Министерство высшего и среднего специального образования республики узбекистан
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
П Р И М Е РРешения задачи сложных электрических цепей переменного тока символическим методом. В качестве примера рассмотрим электрическую схему, походные данные приведены нижеследующей таблице.№2 Таблица.№2
Составим на основании законов Кирхгофа систему уравнения для расчета токов во всех ветвях схемы. Если известны параметры всех элементов цепи ее конфигурация, а требуется определить ток, то при составлении уравнений по закону Кирхгофа рекомендуется придерживаться по такой последовательности: Сначала выбрать произвольные положительные направления токов во всех ветвях электрической цепи, затем составить уравнения для узлов на основании 1-закона Кирхгофа и для контуров на основании 2-закона Кирхгофа. Пусть электрическая цепь содержит «в» ветвей и «у» узлов. На основании первого и второго законов Кирхгофа можно составить соответственно (у-1) и (в-у+1) взаимно неизвестных уравнений. Например, в случаи цепи на рис 1 четырьмя узлами напишем следующие независимые уравнений. Для узла а) İ1 + İ 4 - İ 5 = 0
На основании 2 закона Кирхгофа можно написать в у + 1=6-4+1=3 независимых уравнений. При записи уравнений по второму закону Кирхгофа следует уделять особое внимание уравнению, что составленные уравнения были взаимно независимы. 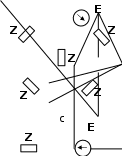 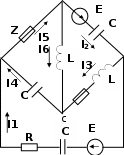 в в в ва а Рис.-1. Исходная электрическая Рис.-2. Развернутая электрическая Контуры выбрать так, чтобы в них вошли ветви схемы, а в каждом из контуров возможно меньше числа ветвей. Контуры взаимно независимы, если каждый следующий контор для второго составляется уравнение, имеет не меньше одной новой ветви. Для электрической цепи по рис1, напишем следующее три независимых уравнений İ1 Z1 – İ2 Z2 –İ3 Z3 = Ė1 İ2 Z2 + İ3 Z3 –İ6 Z6 = Ė2 İ1 Z1 + İ5 Z5 +İ2 Z2 = Ė1+ Ė2 Положительные направления обхода контуров выбран по часовой стрелки для составления уравнений по второму закону Кирхгофа. Итак по первому и второму законов Кирхгофа для электрической цепи рис1 имеем следующее уравнения: İ1 + İ 4 - İ 5 = 0 İ1 Z1 – İ2 Z2 –İ3 Z3 = Ė1 İ 5 – İ 2 - I6 = 0 İ2 Z2 + İ3 Z3 –İ6 Z6 = Ė2 İ2 – İ 1 – İ 3 = 0 İ1 Z1 + İ5 Z5 +İ2 Z2 = Ė1+ Ė2 Совместное решение этих уравнений дает значение токов во всех ветвях электрической цепи. Преобразуем треугольник сопротивлений а в с (рис 1) в эквивалентную звезду. Формула преобразования треугольника на звезду имеет вид. 1 Z Z12Z31 Z Z23Z12 Z Z31Z23 Z12 Z23 Z31 Z12 Z23 Z31 Z12 Z23 Z31 2 3 где Z1 Z2 Z3 –сопротивления лучей эквивалентной звездц. Z12 Z23 Z31 – сопротивления сторн треугольника Для цепи (рис.1) имеем а Z Z4 Z5 Z Z5 Z6 Z Z4 Z6 Z4 Z5 Z6 Z4 Z5 Z6 Z4 Z5 Z6 в с Вычислим знаменатель этих уравнений m = Z4 + Z5 +Z6 =-j6+4+j10 = 4+j4 = 5.66 e- j45 Значений сопротивлений лучей эквивалентной звезды ZZ 6e j90 4 j135 Z 4 5 4.24e 3 j3 Z 4 5 а Z Z 6 5.66ej45 ZZ 4 10ej90 j45 Z 5 6 7.07e 5 j5 Z 4 5 в Z Z 6 5.66ej45 ZZ 6e j90 10ej90 j45 Z 4 6 10.66e 7.5 j7.5 Z 4 5 с Z Z 6 5.66ej45 Электрическая схема после преобразования треугольника сопротивлений abc в эквивалентную звезду приобретает следующий вид 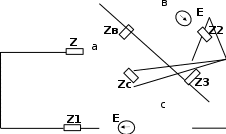 Для полученной электрической схемы определить токи во всех ветвях следующими методами: |
