Вариант 17 надо выполнить. 1-2-3-4 РГР247. Министерство высшего и среднего специального образования республики узбекистан

• Название: Министерство высшего и среднего специального образования республики узбекистан
• Анкор: Вариант 17 надо выполнить
• Дата: 19.10.2021
• Размер: 0.82 Mb.
• Имя файла: 1-2-3-4 РГР247.docx
• Тип: Документы; #250591
• страница: 2 из 28

Порядок расчета

1. Если цепь содержит последовательные и параллельные соединения, еѐ упрощают, заменяя эти соединения эквивалентными

2. 
   Произвольно указывают направления токов во всех ветвях. Еслипринятыенаправлениятоканесовпадаютсдействительнымиприрасчететакиетоки получаютсясознаком«-».
   

3. Составим (у-1) уравнений по I-му закону Кирхгофа (у -число узлов).

4. 
   недостающие уравнения составляют по II – му закону Кирхгофапри этом обход контура можно произвести как по часовой стрелке так ипротивнеѐ.Заположительныйэ.д.с.итокипринимаемтакиенаправлениякоторыесовпадаютснаправлениямиобходаконтура.Направления действияэ.д.с.внутриисточникавсегда принимаетсяот«-
   

» к «+».

5. 
   Полученнуюсистемууравненийрешаютотносительнонеизвестныхтоков.
   

Составим расчетное уравнение для электрической схемы (Рис 1а), выбрав произвольное направление токов в ветвях схемы. Составим уравнение по I-му закону Кирхгофа для узлов а,в,с.


^{a. I1  I3  I2} 

в. c.

I₂  I₄

I I

 I_{6 }

 I^

^{1 4 5} 

Принявнаправление обхода контура по часовой стрелке, составим уравнение по II – му закону Кирхгофа для III-х произвольно выбранных контуров.

Для I

^{контура} 

E E Ir r  Ir r  Ir^

1 3 1 01 1

3 03 3

5 5 _

Для II контура ^

E E Ir r  Ir

• 
  r  Ir^
  

2 3 2 02 2

3 03 3 6 6 _

Для

III

контура ^



0  I₄r₄  I₅r₅  I₆r₆ ^_

II Метод контурных токов (метод ячеек)

Легкозаметить,чторешениеполученнойсистемыиз6–тиуравненийявляетсявесьматруднойзадачей.Поэтомуприрасчетахсложныхэлектрическихцепейцелесообразноприменятьметодконтурныхтоков(методячеек),которыйпозволяетизменитьчислоуравнений составляемых по двум законам Кирхгофа на число уравнений,записанныхпопервомузаконуКирхгофа.Следовательно,системауравнений составленная по методу контурных токов, равна (в-у+1). Прирешении методом контурных токов количество уравнений определяетсячисломячеек(числомконтуров).

Расчет сложных электрических цепей методом контурных токов ведѐтся следующим образом:

1. 
   вводитсяпонятие«контурныйток»произвольнозадаетсянаправление этих токов в ячейках. Удобнее всего все точки указать водномнаправлении,напримерпочасовойстрелке(Рис1а).
   

2. составляем для каждого контура ячейки по II – му закону Кирхгофа, обход контуров производится по часовой стрелке.

3. 
   решая совместно составленные уравнения по II – му законуКирхгофа, определим контурные токи. В этом случае, когда контурныйтокполучилсясознаком«-»,означает,чтоегонаправлениепротивоположно выбранному на схеме.
   

4. токи во внутренних ветвях схемы определяются как сумма или разность соответствующих контурных токов. В случае, когда контурные токи в ветвях совпадают, берут сумму, а когда направлены навстречу из большего вычитают меньший.

5. 
   наложимнаконтурныетокиследующееусловие,т.е.контурные токи должны быть равны по абсолютному значению токамнаименьшейветвисоответствующего контура.
   

I₁  I_k1

I₂  I_k2

I₃  I_k3  I_k1

I₄  I_k3

I₆  I_k1  I_k3

I6  I_k3  I_k2

Чтобы уменьшить число уравнений совместно решаем составленные по II – му закону Кирхгофа, преобразуя треугольник

сопротивлений

r₄ ,r₅ иr₆

в эквивалентную звезду с сопротивлениями

r₇ ,r₈ иr₉

Формулы для преобразования следующие:

7

8
_r r₄ * r_{5 r} r₅ * r<sub>6

r</sub> r₄ * r₆

r₄  r₅  r₆

r₄  r₅

 r₆ r₂  r₅  r₆

9
_{r } 4 *10

 2Ом r ^{10 * 6}  3Ом r

 ^{4 * 6}  1,2Ом

⁷ 4  10  6

⁸ 20

⁹ 20

По II–му закону Кирхгофа , система уравнений для контура получится после преобразования (Рис 2).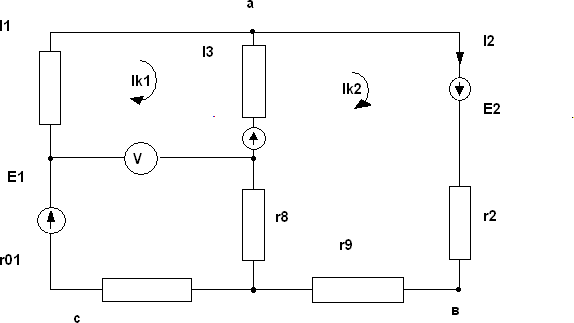

Рис.2

Приняв направление обхода контура по часовой стрелке, составим уравнение по II – му закону Кирхгофа для II-х произвольно выбранных контуров.

^{Ik1r01  r1  r03  r3  r7  r8   Ik2 r03  r3  r8   E1  E2} 

 I r  r r  I r  r  r r r  E  E ^

k1 03 3 8

k 2 03 3 8 9

2 3 

^{Ik10,2  2  1,2  8  2  3  Ik2 1,2  8  3  22 10}





 I_k11,2  8  3  I_k1  1,2  8  3  1,2  24  0
16,4I_k1 12,2I_k2  12

12,2I_k1  14,4I_k2  34

Определители системы:

_{ } 16,4

12,2

12,2

14,4

 16,4 *14,4  12,2* 12,2  236,16 148,84  87,32Ом² 

_{ } 12

¹ 34

12б2

14б4

 12 *14б4  34 /* 12,2  172,8  414,8  587,6вОм

₂ 

16,4

12,2

¹²  16,4 * 34 12 * 12,2  557,6  148,84  706,44вОм

34

Находим контурных токов

_{I } _{1 } 587,6вОм _{ 6,73А}

k1

^Ik2



_ ₂



87,32Ом² 


 ² 
_ 706,44вОм _{ 8,06А}

87,32 Ом

Через контурные токи определим токи ветвей:

I₁  I_k1  6,73A I₂I_k2  8,06A I₃  I_k2  I_k1  8,06  6,73  1,33A

Для электрической цепи (Рис 1а) составим по II закону Кирхгофа,

определимток^I₃

E₁  E₃  Ir₀₁  r₁   I₃ r₀₃  r₃   I₅ * r₅

5
_I E₁  E₃  I₁r₀₁  I₁r₁  I₃r₀₃  I₃r₃

r<sub>5

</sub> 22 10  6,73* 0,2  1,33*1,2  1,33* 8 _

10

_ 22 10 1,34 13,4  1,56  10,4 _ 9,22 _{ 0,922A}

10 10

По первому закону Кирхгофа определим оставшиеся токи:

I₄  I₄  I₁  0,922  6,73  5,81A

I₆  I₂  I₄  8,06   5,81  2,25A

III. Метод узлового напряжения (метод двух узлов)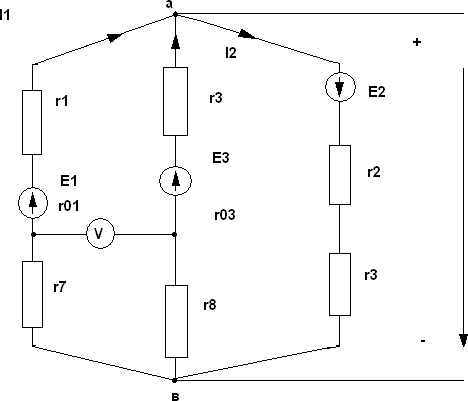

На практике часто используют цепи, в которых параллельно включенонесколько источников энергии и приѐмных устройств, такие цепи удобноанализироватьспомощьюметодаузловогонапряжения(напряжениймежду узлами). Выбираем условие положительного направления токовкак показано на Рис 3, тогда по второму закону Кирхгофа для контурапроходящегопонаправлениюпервойветви:

Рис 3

E₁  I₁r₀₁  r₁  r₇ U_aв

аналогично

E₂  I₂ r₀₂  r₂  r_aU_aв

E₃  I₃ r₀₃  r₃  r₈ U_aв

Определим токи ветвей по закону Ома

I₁ 

E₁  U_aв

r r r

 E₁

 U_aв

* g₁

01 1 7

2
_I E₂  U_aв

 E U

* g

^r02

• 
  r₃
  
• 
  r₉
  

2. 
   aв 2
   

3
_I E₃  U_aв

 E U

* g

^r03

• 
  r₃
  
• 
  r₈
  

2. 
   aв 3
   

Напряжение между двумя узлами а и в:

_{U } E₁g₁  E₂ g₂  E₃ g₃

g

1

2
aв _{ g}

• 
  g₃
  

Определим проводимость ветвей:

g₁  _r

1

• 
  r r
  

 ¹ 

0,2  2  2

1


4,2

 0,238сим

g₂ 

3
g

01

^r02

1

1

• 
  r₂
  

1

7

• 
  r₉
  

_ 1

0 11,2

_ 1

_ 1

2,2

_ 1

 0,454сим

 0,082сим

^r03

• 
  r₃
  
• 
  r₈
  

0,2  8  3

11,2

Напряжение^U<sub>aв

U </sub> E₁g₁  E₂ g₂  E₃ g_{3 } 22 * 0,238  24 * 0,454  10 * 0,082 _ 5,236 10,896  0,82 _



g

1

2
aв _{ g}

• 
  g₃
  

0,238  0,454  0,082

0,774

 ^{ 4,84}  6,25B

0,774

Токи ветвей:

I₁  E U_aв * g₁  22  6,25*0,238  6,724A I₂  E₂ U_aв* g₂  24  6,25*0,454  8,06A I₃  E₃ U_aв* g₃  10  6,25*0,082  1,33A
Метод эквивалентного генератора

На практике часто бывает необходимо изучить режим работы только одной из ветвей сложной электрической схемы. При этом не следует производить громоздкий расчет всей схемы, а целесообразно воспользоваться методом эквивалентного генератора. Согласно этому методу воздействие всех источников сложной электрической цепи на иследуюмую ветвь можно заменить воздействием последовательно включенного с ветвью эквивалентного источника (генератора),

имеющегоэ.д.с

^Еэкв

равную напряжению холостого хода

^Uxx

на зажимах

разомкнутойисследуемойветви,иоконтуренныесопротивлением

r_э,

равное входному сопротивлению схемы со стороны зажимов исследуемой ветви.

Порядокрасчета.

1. Произвольно выбирают направление тока исследуемой ветви.

2. 
   Отключаютисследуемуюветвь.Осуществляютрежимхолостогохода.
   

3. Определяют направление холостого хода разомкнутой ветви.

^Uxx

на зажимах

4. 
   Находят входное(эквивалентное)сопротивлениесхемысостороны
   

зажимов разомкнутой ветви.

5. 
   Вобщемслучаенаходяттокиисследуютветвиповыражению:
   

_I U_xx E

r_э r

где r- сопротивление ветви, в которой определяют ток;

^r_э-входящеесопротивлениесхемысосторонызажимоввыделенной

ветви;

^Uxx

- напряжение холостого хода на зажимах разомкнутой

выделеннойветви;

Е э.д.с., где находится и исследуется ветви.

Если ветвь не содержит Э.Д.С., то она принимается равной нулю.Знаки «+» и «-» выбираются в соответствии с истинным, т.е. еслинаправление э.д.с совпадает с направлением тока, то берѐтся знак «+»впротивномслучае«-».Рассмотримприменениеметодаэквивалентногогенераторанапримересхемы,изображеннойнаРис4.

Рис 4

Решениезадачиразделимнадваэтапа:

1. определение напряжения холостого хода на зажимах разомкнутой ветви.

^Uaв^{ U}xx

2. произвольно выберем положение направления токов. Удаляем из

схемырезистор ^r₆

и по методу контурных токов составляем

системууравнений:


2

• 
  E
  

3 

r
^{Ik1r01  r1  r03  r3  r5  Ik2r03  r3  r5   E1  E3} 

• 
  I_л1
  

^r03

• 
  r₃
  

 r₅  I_л2

03 ^{ r}3

• 
  r₂
  
• 
  r₄
  

r₅

  E ^

^{Ik10,2  2  1,2  8 10 Ik2 1,2  8  10  22 10}





 I_л11,2  8  10 I_л2 1  1,2  8  4  10  24  10

^{21,4 * Ik1 19,2 * Ik2  12} 





19,2 * I_k1  24,2 * I_k2  34

Определители системы:

_{ } 21,4

19,2

19,2

24,2

 21,4 * 24,2 19,2 *19,2  517,88  368,64  149,24

_{ } 12

34

19,2

24,2

 12 * 24,2  34 * 19,2  29,04  652,8  943,2

_{ } 21,4

19,2

¹²  21,4 * 34 12 * 19,2  727,6  230,4  959

34

Определим контурные токи.

^Ik1

 ^1 



943,2


149,24

 6,32A

^Ik2

_ ₂



_ 958

149,24

 6,42A

I₁  I_k2

 6,32A

I₂  I_k2  6,42A I₃  I_k2  I_k1  6,42  6,32  0,1A

Напряжение на разомкнутых ветвях а и в:

U_aввx E₃  I₃r₃  E₂  I₂r₂  10  0,1*8  24  6,42 *1  41,22B

U_aввx E₃  I₃ r₀₃  r₃  E₂  I₂r₂  10  0,1* 9,2  24  6,42 *1  26,66B

3. Определим эквивалентное сопротивление имеет вид, показанный на рис 5.

^rэав

.Схема в этом случае

Рис5

Упростим схему:

R₁^  r₀₁  r₁  0,2  2  2,2Ом R₂^  r₀₂  r₂  0  1  1,0Ом R₃^  r₀₃  r₃  8  1,2  9,2Ом

преобразуем треугольник сопротивлений случае имеет вид, показанный на рис 6.

r_a,r_в

и r_c
схемавэтом