Модуль і. Основи інформаційних технологій в системі охорони здоров'Я. Обробка та аналіз медикобюлогічних даних
 Скачать 5.89 Mb.
|
9. Обчислення критерію вірогідності коефіцієнта кореляції: t = 10. Визначення стандартних значень критеріїв Ст'юдента відповідно трьом програмам вірогідності (95%, 99%, 99,9%) за допомогою таблиці для кількості ступенів свободи (див. вище) v=2n-2. 11. Порівняння коефіцієнтів вірогідності коефіцієнта кореляції стандартними значеннями критеріїв Ст'юдента. Висновок про вірогідність коефіцієнта кореляції. 72 В MS Excel для обчислення цього параметру існує вбудована функція КОРРЕЛ. Практичні завдання сЗь Завдання 1. Обчислення основних статистичних характеристик вибірок. Визначити середнє арифметичне, середнє квадратичне відхилення, помилку репрезентативності, моду та медіану результатів вимірювання швидкості кровотоку 10 пацієнтів до наркозу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| х, | Швидкість кровоточу мл/с | |
| х, | 1 | Л |
| X: | 1 | ,0 |
| Хї | К | 19 |
| х< | 1 | ,22 |
| х5 | 1 | ,4 |
| х6 | 1 | ,0 |
| х7 | 1 | ,1 |
| Хк | 1 | ,3 |
| хУ | 1 | ,2 |
| Хіі) | 1] | ,301 |
| Х^ср | | |
| с | | |
| m | | |
| Мода | | |
| Медіана | | |
Завдання 2. Оцінка вірогідності результатів прямих вимірювань.
Оцінити вірогідність безпосередніх вимірювань швидкості кровотоку 10 пацієнтів до наркозу, використовуючи дані із завдання 1.
Завдання виконати в два способи:
Методом безпосереднього обчислення за поданим вище алгоритмом;
Використовуючи вбудовані функції MS Excel.
Інтерпретуйте отримані результати.
Заедания 3. Оцінка вірогідності відмінностей дослідження двох незалежних вибірок.
Було проведено дослідження дії магнітних полів низької частоти на карциному Герена на четвертий день захворювання (результати досліджень в таблиці:
73
| Контрольна група | Дослідна група |
| 0,027 | 0,075 |
| 0,036 | 0,4 |
| 0,1 | 0,08 |
| 0,12 | 0,105 |
| 0,32 | 0,075 |
| 0,45 | 0,12 |
| 0,049 | 0,06 |
| 0,105 | 0,075 |
В першому стовпчику подані результати інтактної групи, а в другому стовпчику - розмір новоутворення пухлини на яку діяли магнітні поля низької частоти.
Перевірити ефективність впливу магнітних полів на новоутворення пухлини карциноми Герена.
Завдання виконати двома способами:
Безпосередніми обчисленнями за поданим вище алгоритмом;
Використовуючи Пакет аналізу MS Excel.
Алгоритм виконання завдання використовуючи Пакет аналізу MS Excel,
1. Обчислити дисперсії вибірок. Порівняти отримані значення дисперсій.
2. Виконати команду Сервис/Анализ данных/Двухвыборочный t-тест с
разными дисперсиями.
В діалоговому вікні Анализ данных вказати Интервал переменной!', то&го ввести посилання на перший діапазон даних, що аналізуються, і, містить перший стовпчик даних. Аналогічно, вказати Интервал переменной 2. Вказати Выходной диапазон, тобто ввести посилання на комірку, в яку будуть виведені результати.
3. Інтерпретація результатів аналізу.
У вихідний діапазон будуть виведені: середнє, дисперсія, та число дослідів для кожної змінної, різниця середніх, df (число ступенів вільності), P(T<=t) одностороннє, t критичне одностороннє, Р(Т<=І) двостороннє, і критичне двостороннє.
2s. Завдання 4. Оцінка вірогідності відмінностей дослідження двох незалежних вибірок.
На лабораторних щурах проводили дослідження на ембріотоксичність. Результати досліджень подані в таблиці.
| Контрольна група | Дослідна група |
| 1,85 | 2,27 |
| 1,87 | 2,09 |
| 1,87 | 2,09 |
| 2,3 | 2,41 |
| 2,52 | 2,31 |
74
| 1,89 | 2,17 |
| 2,37 | 2 |
| 1,7 | 2,1 |
| 1.7 | 2,02 |
| 1,94 | |
В першому стовпчику подана маса плоду тварин інтактної групи, в другому - маса плоду тварин, яким в порожнину шлунку вводили 0,6% масляного розчину а - токоферолу ацетату з 1 по 10 день вагітності у розрахунку 15мг/кг.
Перевірити доцільність введення масляного розчину а токоферолу ацетату з 1 по 10 день вагітності (гіпотезу рівності середніх при різних об'ємах вибірки).
Завдання 5. Кореляційний аналіз двох випадкових ознак Оцінка вірогідності результатів прямих вимірювань.
В таблиці наведені результати спостережень частоти серцевих скорочень і частоти дихання у групі хворих з певною патологією:
| чсс | 120 | 84 | 105 | 92 | 113 | 90 | so | 72 | 98 | 102 | 95 |
| чд | 20 | 15 | 18 | 16 | 19 | 16 | 15 | 12 | 18 | 20 | 17 |
Необхідно визначити, чи існує взаємозв'язок між частотою серцевих скорочень та частотою дихання при досліджуваній патології.
Завдання виконати використовуючи вбудовану функцію КОРРЕЛ MS Excel.
Алгоритм виконання завдання використовуючи Пакет аналізу MS Excel
Ввести дані до таблиці.
Обчислити значення коефіцієнта кореляції між вибірками.
3. В комірку вставляємо функцію КОРРЕЛ, що викликається наступним
чином Мастер функции/Статистические.
В поле Массив І вводимо дані першої вибірки, в поле Массив 2 - другої.
4. Визначити ступінь залежності між частотою дихання і частотою серцевих
скорочень.
Завдання 6. Кореляційний аналіз двох випадкових ознак.
Визначити, чи існує взаємозв'язок між народжуваністю та смертністю (кількість на 1000 осіб) в м. Одеса, зробити висновки щодо ступеню стохастичного зв'язку. Результати досліджень подані в таблиці:
| Роки | Нар оджуваність | Смертність |
| 1990 | 7,2 | 11,8 |
| 1991 | 7,6 | 10,9 |
| 1992 | 8,1 | 13,1 |
| 1993 | 8,5 | 12,4 |
| 1994 | 9,1 | 15.: |
| 1995 | 9,3 | J2,5 |
| 1996 | 7,4 | 13,5 |
15
| 1997 | | П,4 |
| 1998 | 7,1 | 17,2 |
| 1999 | 7,0 | 15,9 |
| 2000 | 6,6 | J4,2 |
Тестові завдання для самоконтролю
1
. В результаті експерименту, що може бути повторений велику кількістьразів, отримані значення xfl х2у..., *„, які називають:
вибіркою
випадковою величиною
варіаційним рядом
законом розподілу
2. Дискретною випадковою називається величина, яка приймає значення:
з замкненого інтервалу [0;п]
з відкритого інтервалу (0; п)
з напівзамкненого інтервалу зліва або справа
кінцеву кількість значень xh х2,.„, xh
3. Величина, котра може приймати будь-які числові значення в даному
інтервалі значень називається:
дискретною випадковою величиною
неперервною випадковою величиною
випадковою величиною
параметром розподілу випадкової величини
4. Функціональна залежність між значеннями випадкових величин та
ймовірностями з якими вони приймають ці значення називають:
щільністю розподілу
гістограмою розподілу
медіаною розподілу
законом розподілу
5. Властивості, що підлягають оцінці в будь-якій формі називаються:
змінними
системою властивостей
параметрами
варіантою
6. Статистичною сукупністю можна назвати:
контингент студентів, які закінчили медичний університет
контингент дітей віком до 2 років
контингент хворих, що знаходяться у даний момент часу на
76
лікуванні у стаціонарі
□ контингент хворих на туберкульоз віком 30-50 р.
7. Якому закону розподілу підпорядковуються випадкові події такі, як число
викликів швидкої допомоги за певний проміжок часу, черги до лікаря в
поліклініці, епідемії?
Госсета
Біноміальному
Пуассона
Гаусса
8. Група призовників, що пройшли медичне обстеження у військкоматі
протягом року є:
статистичною сукупністю
генеральною сукупністю
9. Набір значень (х/р*2,.дя) випадкової величини X, котрі отримані в
результаті п дослідів, називається:
вибіркою об'єму п
генеральною сукупністю
дискретною випадковою
розподілом випадкової величини
10. Репрезентативною називається вибіркова сукупність, яка:
містить більшу частину елементів генеральної сукупності
містить всі елементи генеральної сукупності
правильно пода£ генеральну сукупність
11. Припущення, котрі відносяться до виду розподілу випадкової величини
або окремих його параметрів є:
функцією розподілу
щільністю розподілу
с тати стич н о ю гі потез ою
параметрамирозподілу
12 Дано вибіркову сукупність: {115; 115; 115; 120; 120; 120; 120; 120; 125). Визначити моду.
115
120
125
13. Дано вибіркову сукупність; '115: 115; 115; 120; 120: 120. 120; 120; 125 |. Визначити моду.
115
120
77
□ 125
14. Ймовірність з якою може бути відхилена нульова гіпотеза, коли вона є
вірною, називається:
рівень значущості
похибкою експерименту
довірчою ймовірністю
15. При проведенні досліджень необхідно забезпечити наступні вимоги до
вибірки:
структурну відповідність
однорідність
репрезентативність
співпадання умов спостережень
16. Значення коефіцієнта кореляції може змінюватися від
17. Що характеризує абсолютне значення коефіцієнта кореляції
стохастичного взаємозв'язку між випадковими величинами:
силу та напрям
напрям та щільність
розсіювання та напрям
силу та щільність
18. Знак коефіцієнта кореляції вказує
на щільність кореляції
на напрям стохастичного зв'язку
на силу стохастичного зв'язку
на ступінь розсіювання між випадковими величинами
78
МОДУЛЫ1. МЕДИЧНІ ЗНАННЯ ТА ПРИЙНЯТТЯ РІШЕНЬ У МЕДИЦИНІ
Формалізація та алгоритмізація медичних задач
Конкретні ц'иіі заняття: трактувати поняття алгоритму, властивості алгоритму:
інтерпретувати структурні схеми алгоритмів; демонструвати вміння формалізувати га алгоритмізувати медичні задачі
Основні поняття теми
Ф
ормалізація, алгоритмізація, алгоритм, способи подання алгоритмів (словесний, символічний, графічний), властивості алгоритму (визначеність, масовість, дискретність, результативність), типи алгоритмів (лінійний, розгалужений, циклічний), розгалуження, умова, цикл, цикл-ДО, цикл-ПОКИ.К
ороткі теоретичні відомостіОснови формалізації та алгоритмізації медичних задач
Формалізація -- процес подання інформації про об'єкт, процес, явище в формалізованому вигляді. В результаті аналізу задачі визначається специфіка даних, вводиться система у.мовних позначень, встановлюється прина.іежність її до одного з класів задач (наприклад, математичні, фізичні, медичні тощо).
Якщо певні аспекти розв'язуваної задачі можна виразити в термінах якої-небудь формальної моделі (визначеної структури, що використовується для подання даних), то це, безумовно, необхідно зробити, оскільки в цьому випадку в рамках формальної моделі можна дізнатись, чи існують методи й алгоритми розв'язання поставленої задачі. Навіть якщо вони не існують, то використання засобів і властивостей формальної моделі допоможе в побудові розв'язку задачі.
Формалізована медико-біологічна задача повинна бути алгоритмізованою. Під алгоритмізацією розуміють метод опису систем або процесів шляхом створення алгоритмів їх функціонування.
Під алгоритмом зазвичай розуміють правило, що вказує дії, в результаті виконання яких отримуємо бажаний результату. Таку послідовність дій називають алгоритмічним процесом, а кожну дію його кроком. Етап алгоритмізації в загальному випадку настає лише тоді, коли зрозуміла постановка задачі, коли існує чітка формальна модель, в рамках якої буде, власне, відбуватися розв'язання задачі. З цієї точки зору процес підготовки задачі передбачає:
постановку задачі - визначення її змісту та вихідних даних;
розробку алгоритму розв 'язання - вибір методу розв'язування та опис
послідовності дій;
представлення алгоритму розв'язання -- побудова структурної схеми алгоритму.
Алгоритми та їх властивості.
79
Алгоритм -- упорядкований скінчений набір чітко визначених правил для розв'язування задач за скінчену кількість кроків.
Говорячи про алгоритми, необхідно розглянути джерела їх виникнення (див. рис. 35).
П
рактикаДжерела виникнення алгоритмів
Наука
І
Комбінації та модифікації |існуючих алгоритмів
" і
Рис. 35. Джерела виникнення алгоритмів
Будь-який алгоритм повинен задовольняти наступним властивостям (рис. 36):
визначеність - алгоритм не повинен містити вказівок, зміст яких може бути сприйнятий неоднозначно. Крім того, при виконанні алгоритму ніколи не повинна з'являтися потреба у прийнятті будь-яких рішень, котрі непередбачені укладачем алгоритму.
масовість - алгоритм складається не для розв'язання однієї конкретної задачі, а для цілого класу задач одного типу. В простому випадку ця варіативність алгоритму забезпечує можливість використання різних допустимих вихідних даних.
дискретність процес, який описується алгоритмом, має бути поділений на послідовність чітко відокремлених одна від одної вказівок, котрі утворюють дискретну структуру алгоритмічного процесу.
результативність - при точному виконанні всіх вказівок алгоритму процес прийняття рішення (отримання результату) повинен закінчитися через скінчену кількість кроків і при цьому має бути отримана відповідь на поставлені в задачі питання.
Р
езультативність
Визнач віність
Масовість
Д
искретністьР
ис. 36. Властивості алгоритмів80
Графічний спосіб подання алгоритмів - зображення алгоритму у вигляді структурної схеми, котра складається з окремих блоків. Цей спосіб подання алгоритму є найбільш зручним і наочним.
При поданні задачі графічним способом застосовують такі основні види блоків (табл. 16):
Таблщя 12. Основні елементи блок схеми алгоритму
| Зображення блоку | Призначення |
| і 1 1 | Блок у вигляді прямокутника символгіус ІШКОЇШІІІІЯ ПОВНИХ ВКІОІВОК Задачі. |
| і | С грілка вказус напрям ходу виконання умои j вдачі. |
| | Блок у вигляді ромба символгіус перевірку никонання певного твердження і метою прийняття рішення про напрям ходу подальшого в її конання умони задачі. Всередині блока описусгься ум он а, яку jpeGa перенірити. Можливі операції вказуються на виходах -лініях, що шіходять і блока. |
| ґ" Початок J) ( Кінець J) | У вигляді овальних блоків зображуються початок і кінець алгоритму. |
| -?- | Сполучне kojjo використовують при поіребі звести кілька ліній в одну. |
При складанні структурної схеми алгоритму укладач повинен дотримуватися наступних правил, так званих правил для складання структурної схеми алгоритму:
- будь-який алгоритм повинен мати початок і кінець;
усі блоки, крім перевірки умови? мають тільки один вихід;
усі блоки алгоритму мають не більше одного входу;
лінії алгоритму не можуть розгалужуватися.
Демонстраційний приклад
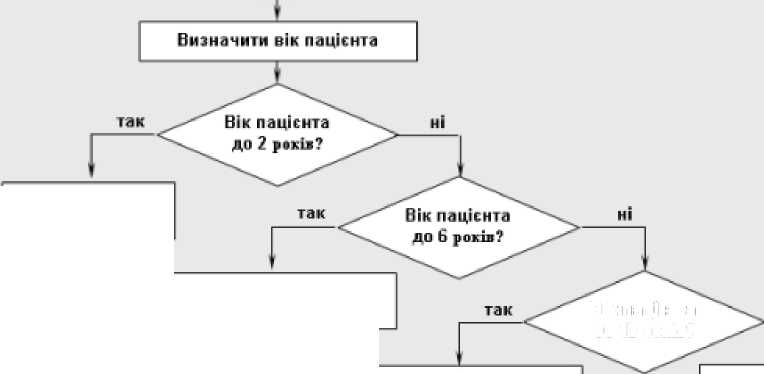
Складемо структурну схему алгоритму дозування серцевого препарату Корглікону залежно від віку паціента? згідно формалізованої інструкції застосування (табл. 17).
Таблиця ІЗ. Інструкція застосування препарату Карглікон
| Вік (років) | Доза (мг) |
| До2 | не призначається |
| 2-6 | (М-0,5 |
| 6-12 | 0.5-0,75 |
| більше 12 | 0J5-1,0 |
SI
Враховуючи правила складання структурної схеми, починаємо створення схеми з блоку «Початок». Оскільки дозування препарату залежить від віку пацієнта, то в наступних блоках визначимо вік пацієнта та перевіримо його належність до кожного з вікових проміжків, визначених в інструкції (блок перевірки іверлжень - ромб). Бід блоку перевірки тверджень відходить завжди дві стрілки - «так» і «ні». Над стрілкою «так» дамо вказівку (блок у вигляді прямокутника) про дозування препарату відповідно до певного вікового проміжку. За стрілкою «ні» продовжимо перевірку наступного вікового періоду (дивись рисунок 37).
ІІІІЧ'ІІІІК
репарат паї на