Никифоров_учебное пособие. московский государственный университет дизайна и технологии

• Название: московский государственный университет дизайна и технологии
• Анкор: Никифоров_учебное пособие.doc
• Дата: 11.05.2017
• Размер: 17.89 Mb.
• Имя файла: Никифоров_учебное пособие.doc
• Тип: Учебное пособие; #7451
• страница: 7 из 10

3. ПОЗИЦИОННЫЕ ЗАДАЧИ
Это задачи, в которых решается вопрос о взаимном порядке, взаимном положении и взаимном пересечении геометрических объектов.

Задачи на взаимный порядок и взаимное положение геометрических объектов, а также задачи на взаимную принадлежность геометрических объектов были разобраны в разделах 1 и 2. Эти задачи не имеют самостоятельной методики и опираются на решение других позиционных задач. Наибольший практический интерес представляют задачи на пересечение поверхностей и задачи на пересечение линии и поверхности. Изучение этих задач рассмотрим методом индукции, т. е. от частного к общему.

В этих двух типах задач можно выделить три группы задач:

1) Оба пересекающихся геометрических объекта занимают проецирующее положение;

2) Один из пересекающихся геометрических объектов занимает проецирующее положение, другой – непроецирующее;

3) Оба пересекающихся геометрических объекта занимают непроецирующие положения.

Проецирующими геометрическими объектами могут быть: прямая, плоскость, цилиндрическая поверхность (см. рис. 1.11).

Рассмотрим первый тип задач – задачи на пересечение поверхностей.

Вначале рассмотрим задачи на пересечение проецирующих геометрических объектов и когда один из объектов непроецирующий. После этого рассмотрим задачи на построение линии пересечения непроецирующих геометрических объектов.
3.1. Пересечение геометрических объектов, когда

оба геометрических объекта проецирующие
3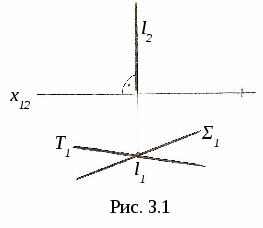.1.1. Построение линии пересечения двух горизонтально-проецирующих плоскостей. На рис. 3.1 заданы горизонтально-проецирующие плоскости Σ и Τ. Так как обе плоскости горизонтально-проецирующие, то и линия их пересечения ℓ также является горизонтально-проецирующей прямой, т. е. Σ ∩Τ=ℓ, Σ_┴Π₁и Τ_┴Π₁ , следовательно, ℓ_┴Π_1.

3.1.2. Виды линий пересечения прямого кругового цилиндра с плоскостями. Такими линиями являются:

- окружность, когда секущая плоскость Τ перпендикулярна оси цилиндра;

- две параллельные прямые, если плоскость Ω параллельна оси цилиндра ί;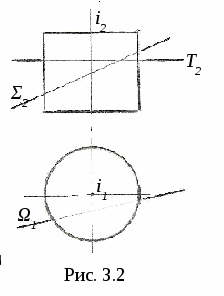

- эллипс – в любом другом положении секущей плоскости Σ (рис. 3.2).

На рисунке 3.3 дано построение проекций и натуральной величины линии пересечения (эллипс) прямого кругового цилиндра с плоскостью Σ. На плоскость Π₂ эллипс проецируется в виде отрезка, совпадающего с Σ₂, на Π₁ – в виде окружности.

Таким образом, фронтальная и горизонтальная проекции линии пересечения на чертеже в данном случае уже очевидны (определены). Натуральная величина эллипса построена по точкам с помощью введения дополнительной плоскости Π₅ ; х₂₅||Σ₂, т.е. Π₅||Σ и Π_5┴ Π_2.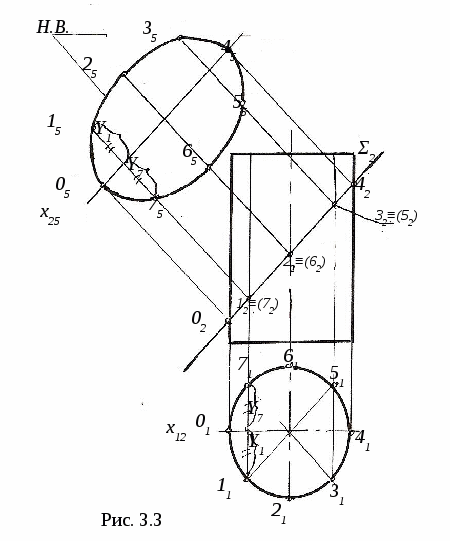



3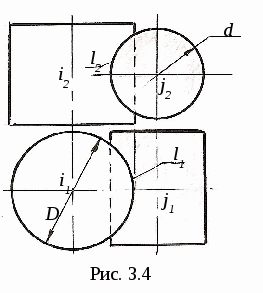.1.3. Определение проекций линии пересечения двух круговых цилиндров. На рис. 3.4 ось ί одного цилиндра задана перпендикулярно Π₁, ось j другого цилиндра перпендикулярна Π₂, т. е. обе поверхности являются проецирующими.

Следовательно, фронтальная проекция линии пересечения цилиндров ℓ (ℓ₂)совпадает с фронтальной проекцией боковой поверхности цилиндра с осью j(окружностью диаметра d), а горизонтальная проекция ℓ (ℓ₁)совпадает с горизонтальной проекцией боковой поверхности цилиндра с осью i(окружностью диаметра D).

Проекции линии пересечения ℓ (ℓ₁,ℓ₂)должны находиться внутри очерков поверхностей.

Итак, когда оба пересекающихся геометрических объекта проецирующие, то проекции линии пересечения на чертеже уже заданы, их надо только отметить.
3.2. Пересечение геометрических объектов, когда один

из геометрических объектов проецирующий,

а другой непроецирующий
3.2.1. Построение линии пересечения двух плоскостей. На рис. 3.5, а заданы Τ (а∩b) – плоскость общего положения, и Σ – фронтально-проецирующая плоскость. Фронтальная проекция линии пересечения плоскостей ℓ (ℓ₂) совпадает со следом плоскости Σ (Σ₂), т. е. Σ₂≡ℓ₂. Горизонтальную проекцию линии ℓ (ℓ₁) находим по принадлежности линии ℓ плоскости Τ (рис. 3.5, б)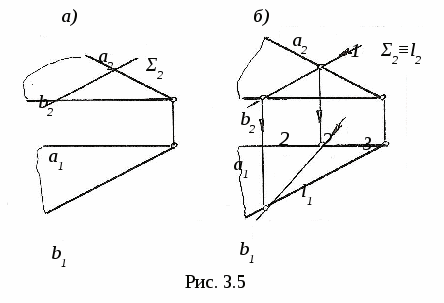



3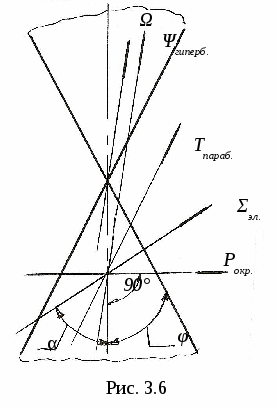.2.2. Линии пересечения конической поверхности с плоскостями. Прямой круговой конус имеет пять видов линий пересечения в зависимости от положения секущей плоскости по отношению к оси конуса.

Обозначим угол между образующей конуса и его осью буквой φ, а угол между секущей плоскостью и осью конуса буквой α (рис. 3.6).

Возможны следующие виды линий пересечения:

1) если α=90°, то плоскость P пересекает поверхность по окружности;

2) если 90°>α>φ, то плоскость Σ пересекает поверхность по эллипсу;

3) если α=φ, т. е. секущая плоскость Τ параллельна одной образующей, то поверхность пересекается по параболе;

4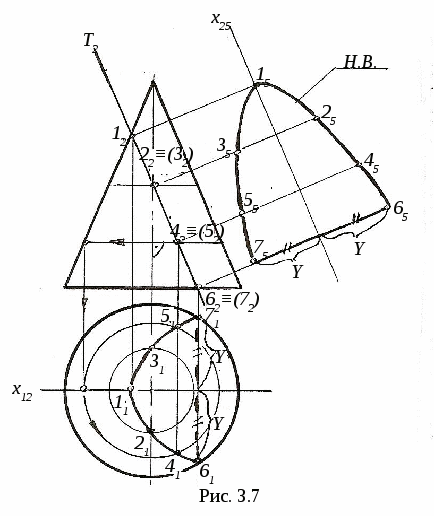) если 0≤α<φ, т. е. секущая плоскость Ψ параллельна двум образующим, то поверхность пересекается по гиперболе;

5) если 0≤ α<φ и секущая плоскость Ω проходит через вершину конуса, то поверхность пересекается по двум образующим.

3.2.3. Построение проекций и натуральной величины линии пересечения конической поверхности с плоскостью. На рис. 3.7 заданы коническая поверхность и фронтально-проецирую-щая плоскость Т. В данном случае при пересечении получается парабола. Так как плоскость Τ_┴ Π₂ , то фронтальная проекция параболы совпадает с Τ₂.

Для того, чтобы построить горизонтальную проекцию параболы, на её фронтальной проекции отмечаем ряд точек 1₂,…,7₂. Горизонтальные проекции точек 1₁,…,7₁ строим с помощью параллелей.

Натуральную величину параболы строим по точкам с помощью введения дополнительной плоскости проекций Π₅||Τ. Так как парабола является симметричной фигурой, то для удобства построений ось х₁₂ взята совпадающей с осью симметрии горизонтальной проекции конуса. Ось х₂₅||Τ₂. Построение видно из чертежа.

3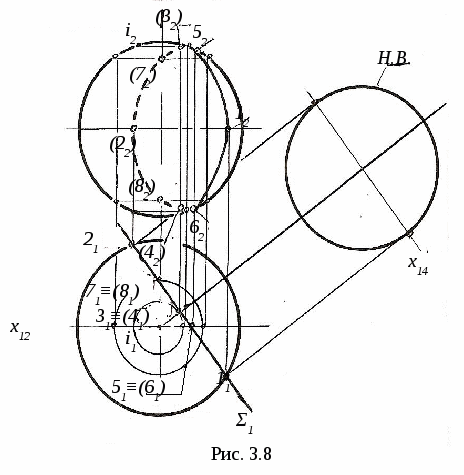.2.4. Построение проекций и натуральной величины линии пересечения сферы с плоскостью. При пересечении сферы с любой плоскостью образуется окружность.

На рис. 3.8 сфера пересекается горизонтально-проецирующей плоскостью Σ. Окружность, получаемая при пересечении плоскости Σ со сферой, при проецировании на Π₁ совпадает со следом плоскости Σ (Σ₁) – это отрезок 1₁-2₁. На фронтальную плоскость Π₂ окружность проецируется в виде эллипса, причём 1₂-2₂ – малая ось эллипса, 3₂-4₂ – большая ось эллипса. Промежуточные точки можно построить с помощью параллелей.

Натуральная величина окружности построена с помощью введения дополнительной плоскости проекций Π₄||Σ. Ось х₁₄проводим параллельно Σ₁.

Построение видно из чертежа.

3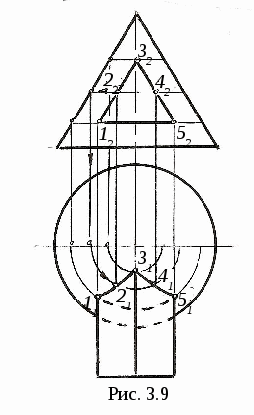.2.5. Построение проекций линии пересечения конуса и призмы. На рис. 3.9 заданы конус и призма. В данном случае три грани призмы перпендикулярны Π₂, поэтому фронтальная проекция линии пересечения совпадает с фронтальной проекцией призмы 1₂-3₂-5₂.

Горизонтальная проекция линии пересечения построена по принадлежности конусу с помощью параллелей.

Таким образом, когда один из пересекающихся геометрических объектов проецирующий, а другой непроецирующий, то одна из проекций линии пересечения на чертеже уже определена, а другая проекция определяется по принадлежности непроецирующему геометрическому объекту.
3.3. Пересечение геометрических объектов, когда

оба геометрических объекта – непроецирующие
При взаимном пересечении поверхностей образуется общее множество точек, представляющих собой пространственную кривую линию. В частных случаях кривая распадается на несколько частей, каждая из которых может быть и плоской. Линию взаимного пересечения ещё называют линией перехода.

Пусть заданы две поверхности Φ и Τ (рис. 3.10). Требуется построить линию их пересечения ℓ = Φ ∩Τ.

Линию пересечения поверхностей строят по точкам, применяя способ вспомогательных поверхностей-посредников (плоскости, сферы и т. д.). Заданные поверхности пересекают вспомогательными поверхностями. Желательно, чтобы при пересечении вспомогательных поверхностей с заданными получались графически простые линии – прямые, окружности. Для упрощения построения в качестве поверхностей-посредников – применяют проецирующие поверхности.

3.3.1. Алгоритм построения линии пересечения двух поверхностей. Предварительно выполняем следующие действия:

1) Определяем, какие поверхности пересекаются.

2) Определяем характерные точки, принадлежащие линии пересечения (наивысшая и наинизшая, самая правая и самая левая точки пересечения и т. п., а также точки, принадлежащие очерковым и другим характерным образующим поверхностей).

3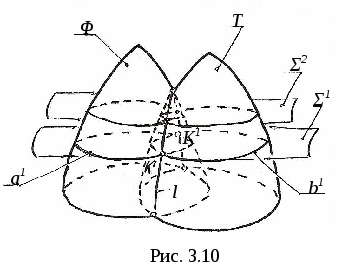) Определяем, какой способ можно применять для построения линии пересечения.

Далее переходим к собственно построению линии пересечения:

4) Для определения промежуточных точек пересекаем обе поверхности вспомогательной поверхностью Σ ¹:

а) строим линию пересеченияа¹= Σ ¹∩Φ;

б) строим линию пересеченияb¹= Σ ¹∩Τ¹;

в) отмечаем точки пересечения линий К¹= а¹∩ b¹.

Для построения других точек, принадлежащих линии пересечения, вводим ещё несколько вспомогательных поверхностей Σ ^ί и получаем ещё несколько точек К ^ί. Множество полученных точек будет представлять собой линию пересеченияℓ двух поверхностей;

5) определяем видимость линии пересечения и очерков поверхностей.

3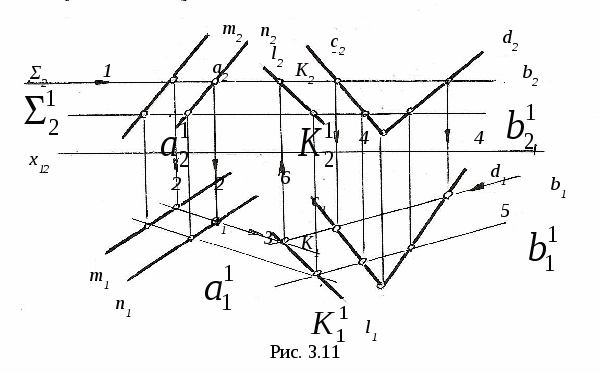.3.2. Построение линии пересечения двух плоскостей общего положения. На рис. 3.11 заданы плоскости Φ (m||n) и Τ (c∩d). Построение линии пересечения плоскостей заключается в нахождении двух точек, принадлежащих этой линии, т. к. при пересечении двух плоскостей получается прямая линия. Для определения двух точек достаточно двух плоскостей-посредников. На рис. 3.11 для нахождения одной точки K введена горизонтальная плоскость Σ || Π₁.

Согласно указанному выше алгоритму:

Σ∩Φ=а, Σ∩Τ=b и а∩b=K.

Для определения второй точки K¹ пересекаем плоскости Φ и Τ плоскостью Σ¹ и аналогично строим вторую точку K¹. Соединив точки K и K¹, получаем линию пересечения ℓ = Φ ∩Τ.

3.3.3. Построение проекций линии пересечения двух кривых поверхностей с помощью вспомогательных секущих плоскостей. Сущность способа заключается в проведении семейства плоскостей, пересекающих обе поверхности по наиболее простым линиям – прямым и окружностям, либо пересекающих поверхности по кривым, проецирующимся в виде прямых и окружностей.

Н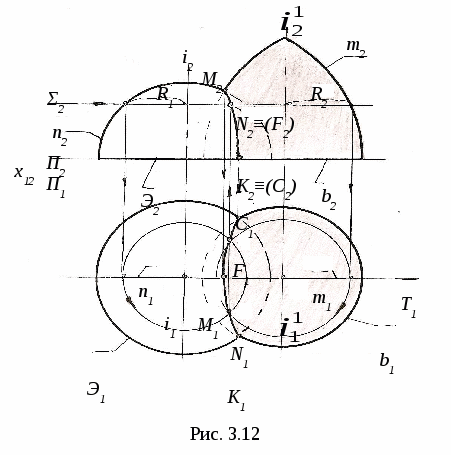а рис. 3.12 показано построение проекций линии пересечения полусферы и тора.

Сначала отмечаем характерные точки: M –наивысшую, C и K – наинизшие, Fи N - промежуточные.

Точка M принадлежит линии пересечения поверхностей, т. к. она располагается в общей фронтальной плоскости симмет-ии Τ (Τ₁), т. е. глав-ные фронтальные меридианы n и mпересекаются в точке M, или n₂∩m₂=M₂._. M₁находится на линии проекционной связи.
Наинизшие точки C и K находятся на пересечении экватора полусферы – Э и экватора тора b, т. е. Э₁∩b₁=K₁ и C₁. На линии проекционной связи находим точки K₂≡C₂.
Промежуточные точки F и N находим с помощью вспомогательной горизонтальной плоскости Σ (см. вышеприведённый алгоритм), которая пересекает полусферу по окружности радиуса R₁и тор – по окружности радиуса R₂. Эти окружности лежат в одной плоскости и пересекаются; их горизонтальные проекции пересекаются в точках N₁ и F₁, а проекции N₂≡F₂расположены на линии проекционной связи на Σ₂.

Проведя ещё несколько вспомогательных горизонтальных плоскостей, можно построить аналогичным путём ещё ряд промежуточных точек.

Соединив эти точки плавной кривой, получим проекции линии пересечения полусферы и тора. Затем определяем видимость линии пересечения и очерковых линий.

3.3.4. Пересечение соосных поверхностей вращения. Это поверхности, имеющие общую ось вращения ί.

На рис. 3.13 изображены соосные поверхности конуса и сферы, на рис. 3.14 – соосные цилиндр и сфера.

Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения ί.

На рис. 3.13 и 3.14 поверхности пересекаются по окружностям a и b, концы диаметров (1-3 и 2-4) которых получаются при пересечении очерковых линий (главных меридианов).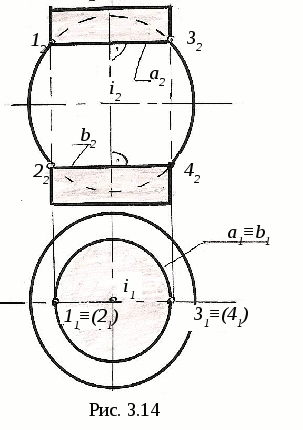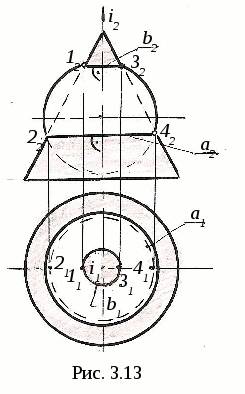







Это свойство соосных поверхностей положено в основу способа вспомогательных секущих сфер.

3.3.5. Построение проекций линий пересечения поверхностей вращения с помощью вспомогательных сфер (концентрических). В этом способе при построении линии пересечения заданные поверхности пересекают сферами, соосными с данными поверхностями, причём центры всех вспомогательных сфер находятся в точке пересечения осей вращения.

Вспомогательная сфера пересекает каждую из заданных поверхностей по окружности. Эти окружности, расположенные на одной и той же сфере, будут пересекаться друг с другом. Точки пересечения окружностей принадлежат искомой линии пересечения.

Для применения этого способа необходимы следующие условия:

1) обе пересекающиеся поверхности являются поверхностями вращения;

2) оси вращения поверхностей должны пересекаться и располагаться в плоскости, параллельной одной из плоскостей проекций.

На рис 3.15 показано построение линии пересечения двух прямых круговых конусов Φ ∩Τ. Оси вращения ί и j пересекаются в точке O (O₁ , O₂) и параллельны плоскости Π₂. Это и будет центр вспомогательных сфер.

При пересечении очерковых линий конусов получаются точки: A – самая высокая и B – самая низкая, принадлежащие искомой линии пересечения.

При пересечении двух конусов плоскостью Γ (Γ₂) получаем точки C и D: δ₁∩n₁=C₁и D₁ , и на линии проекционной связи определяем точки C₂ и D₂.

Далее необходимо отметить границы введения вспомогательных сфер.

Максимальный радиус вспомогательной сферы (R_max=O₂B₂) определяется расстоянием от точки пересечения осей до наиболее удалённой точки пересечения очерковых линий, а минимальный радиус сферы R_minравен радиусу сферы Σ, вписанной в наибольший из очерков поверхностей, т. е. в поверхность Φ, касающейся её по окружности m (m₁, m₂), и пересекающей другую поверхность T по окружности 3-4 (3₂-4₂). Плоскости этих окружностей перпендикулярны осям вращения поверхностей. При пересечении этих окружностей получаются точки K и , принадлежащие линии пересечения поверхностей: Σ∩Φ=1-2, Σ∩T=3-4 и далее 1-2∩3-4=K и (1₂-2₂∩3₂-4₂=K₂≡).

По такому же алгоритму с помощью промежуточных сфер строятся другие точки, принадлежащие линии пересечения,.

Радиусы промежуточных сфер берут произвольно в пределах между R_min и R_max.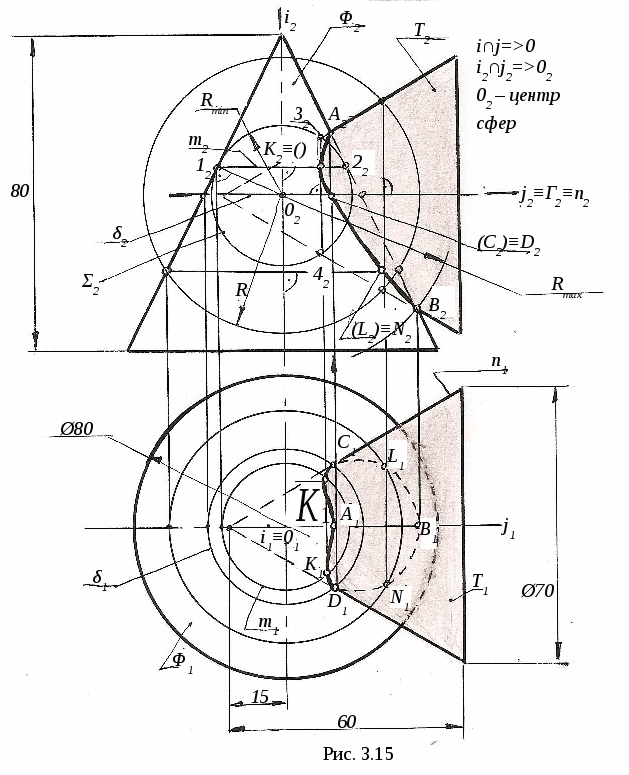



На чертеже проведена одна из промежуточных сфер радиуса R и построены точки L (L₁, L₂) и N (N₁, N₂).

Проведя ещё несколько вспомогательных сфер, получим ряд точек, принадлежащих линии пересечения. Соединив одноимённые проекции полученных точек, получаем проекции линии пересечения. Затем определяем видимость линии пересечения и очерковых линий.