Никифоров_учебное пособие. московский государственный университет дизайна и технологии

• Название: московский государственный университет дизайна и технологии
• Анкор: Никифоров_учебное пособие.doc
• Дата: 11.05.2017
• Размер: 17.89 Mb.
• Имя файла: Никифоров_учебное пособие.doc
• Тип: Учебное пособие; #7451
• страница: 8 из 10

3.4. Пересечение линии с поверхностью
3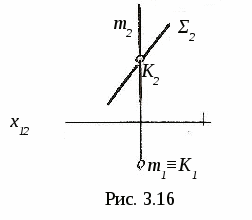.4.1. Пересечение линии с поверхностью, когда оба геометрических объекта проецирующие. На рис. 3.16 показано пересечение фронтально-проецирующей плоскости Σ и горизонтально-проецирующей прямой m.

Так как плоскость Σ и прямая mпроецирующие, то проекции точки их пересечения (точка K) на чертеже уже определены, их надо только отметить (K₂ и K₁).

3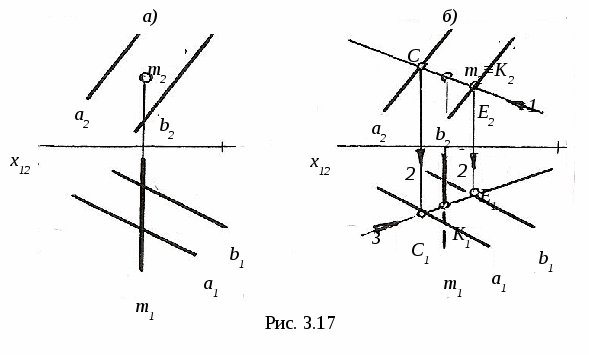.4.2. Пересечение линии с поверхностью, когда один из пересекающихся геометрических объектов проецирующий, а другой – непроецирующий. На рис. 3.17 показано определение точки пересечения плоскости Σ (a||b)и прямой m.Σ∩m=K.

Так как прямая m_┴Π₂ (рис. 3.17, а), то K₂≡m₂ (рис. 3.17, б), а K₁ находим из условия принадлежности точки K плоскости Σ с помощью вспомогательной прямой CEΣ. Ход построения указан на чертеже.

На рис. 3.18 показано построение точек пересечения прямых d и mс конической поверхностью Φ. d∩Φ=K, m∩Φ=C и B.

Так как d_┴Π₁, то K₁≡d₁, а K₂ находим с помощью образующей S.

П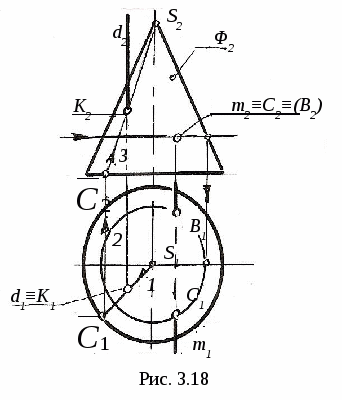рямая m_┴Π₂, поэтому фронтальные проекции C₂ и B₂точек пересечения прямой m с конусом совпадают с m₂, а C₁ и B₁ находим с помощью параллели.

3.4.3. Пересечение линии с поверхностью, когда оба геометрических объекта непроецирующие. Для определения точек пересечения линии с поверхностью (рис. 3.19) необходимо:

1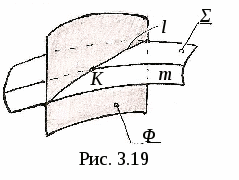) заключить линию (m)во вспомогательную поверхность: Σm. Желательно, чтобы при пересечении Σ с заданной поверхностью Φ получались прямые или окружности;

2) определяем линию пересечения ℓ вспомогательной поверхности Σ и Φ. Σ∩Φ=ℓ;

3) определяем точки пересечения построенной линии ℓ с m, то есть ℓ∩m=K^ί;

4) определяем видимость заданной линии.

На рис. 3.20 показано построение точки пересечения прямой общего положения m с плоскостью Φ (a||b) (рис. 3.20, а) иm∩Φ=K(рис. 3.20, б).

Ход построения:

1) заключаем прямую m во фронтально-проецирующую плоскость Σ (Σm), то есть через m₂ проводим Σ₂;

2) строим линию пересечения плоскостей Σ и Φ. Это прямая CM (C₁M₁, C₂M₂). CM=Σ∩Φ;

3) определяем точку K пересечения m с CM. Сначала определяем точку K₁(K₁= m₁∩C₁M₁), а затем с помощью линии проекционной связи - точку K₂ (K₂m₂);

4) видимость прямой m и плоскости Φ определяем с помощью конкурирующих точек: на Π₁ – с помощью N и F; на Π₂ – с помощью L и M.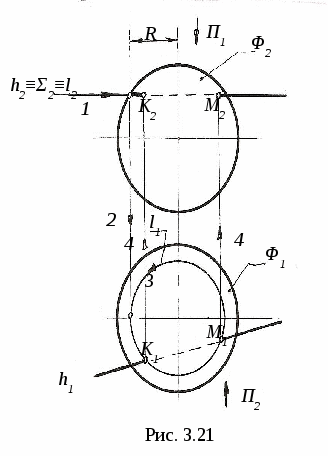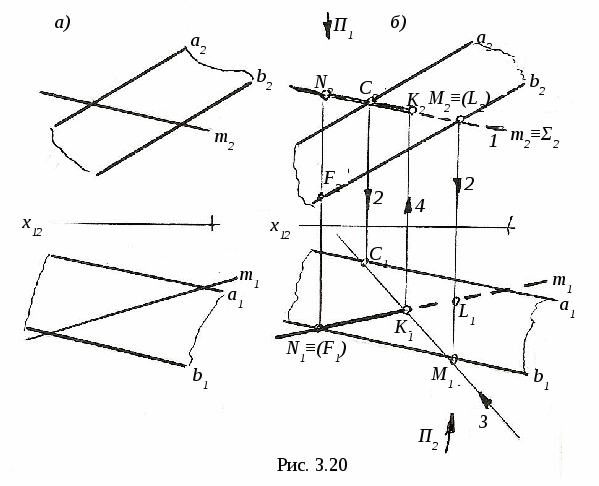





На рис. 3.21 показано построение точек пересечения горизонтали h со сферой Φ.

Ход построения:

1) заключаем прямую h в горизонтальную плоскость Σh (Σ₂≡h₂);

2) строим линию пересечения ℓ (окружность радиуса R) плоскости Σ со сферой. Σ ∩Φ=ℓ;

3) определяем точки пересечения линии ℓ с горизонталью h. ℓ∩h=K и M. Сначала отмечаем точки K₁ и M₁, а затем с помощью линий проекционной связи находим K₂ и M₂ на h₂;

4) определяем видимость линии m.

Построение точек пересечения прямой общего положения m со сферой Φ приведено на рис 3.22.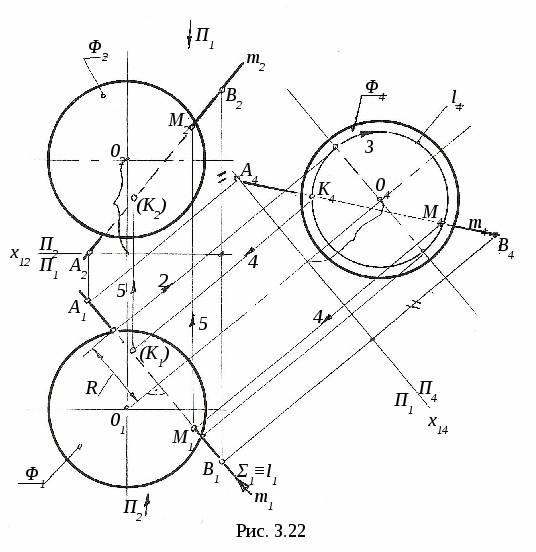



Для определения искомых точек пересечения выполним следующие построения:

1) заключаем прямую m в горизонтально-проецирующую плоскость Σ (Σ₁m₁).

При пересечении Σ со сферой получается окружность, которая на Π₂ спроецируется в виде эллипса. Чтобы избежать построения эллипса, с помощью метода замены плоскостей проекций преобразуем прямую m в положение линии уровня, тогда дальнейшее построение будет подобно примеру на рис. 3.21.

Для этого:

2) на прямой m задаём две точки A и B;

3) проводим дополнительную плоскость Π₄||m (х₁₄||m₁);

4) Проецируем на Π₄ прямую AB и сферу. В новой системе Π₁-Π₄ прямая m стала фронталью (m₁, m₄);

5) Σ∩Φ=ℓ (окружность радиуса R);

6) ℓ ∩ m=K и M, то есть ℓ₄ ∩ m₄=K₄ и M₄ . K₁ и M₁, K₂ и M₂ находим по линиям проекционной связи;

7) Определяем видимость m на Π₁ и Π₂.

На рис. 3.23 показано построение точек пересечения прямой общего положения m с конусом.

В данном случае удобнее всего, чтобы вспомогательная плоскость Σ пересекала конус по двум образующим, то есть вспомогательная плоскость должна проходить через вершину конуса S. Эта плоскость уже задана на чертеже прямой m и точкой S, то есть Σ (S, m).

Для удобства построений переходим к заданию плоскости Σ пересекающимися прямыми. Для этого на прямой m задаём точку E (E₁, E₂) и соединяем её с вершиной S. Теперь плоскость Σ задана двумя пересекающимися прямыми: Σ (m∩SE).

Далее строим линию пересечения Σ с Π₁, это линия CM. Для этого находим горизонтальные следы прямых mиSE, это C₁ и M₁.

Горизонтальный след Σ (CM) и основание конуса лежат в одной плоскости, поэтому линия CM пересекает основание конуса в точках A и B, которые соединяем с вершиной S и получаем образующие ASи SB, по которымΣ пересекает конус.

Затем строим точки пересечения ASи SB с прямой m. AS∩m=K, BS∩m=F.

Таким образом точки K и F - искомые точки. Далее определяем видимость прямой m.
3.5. Перпендикулярные геометрические объекты
3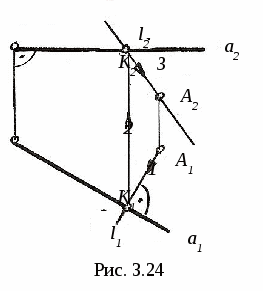.5.1. Перпендикулярные прямые. На рис. 3.24 показано построение прямой ℓ, проходящей через точку Aи перпендикулярной прямой a.

Прямая a - горизонталь, то есть a||Π₁.

Из теоремы о частном случае проецирования прямого линейного угла (см. рис. 1.10) следует, что если одна сторона прямого линейного угла параллельна какой-либо плоскости проекций, то на эту плоскость прямой угол спроецируется в натуральную величину.

Следовательно, через A₁ проводим ℓ_1┴ a₁, отмечаем точку K₁, находим K₂ по линии проекционной связи на a₂ и проводим ℓ₂, то есть ℓ_1┴ a₁ так как a||Π₁ и ℓ_┴ a (рис. 3.24).

3.5.2. Перпендикулярные прямая и плоскость. Как известно, прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости.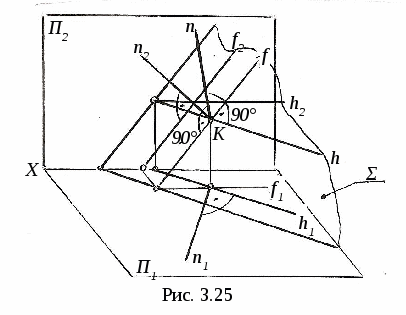

При построениях удобно применять в качестве пересекающихся прямых горизонталь h и фронталь f.

Пусть необходимо (рис. 3.25) из точки KΣ восставить перпендикуляр n  Σ.

Для этого через точку K проведём горизонталь h и фронталь f и перпендикулярно к ним проведём прямую n (n_┴ h и n_┴ f).

На основании теоремы о частном случае проецирования прямого линейного угла угол между n и h на Π₁ спроецируется без искажения, то есть угол между горизонтальной проекцией горизонтали h₁ и горизонтальной проекцией перпендикуляра n₁ будет прямым (n_1┴ h₁).

Аналогичным образом можно доказать, что если n_┴ f, то n_2┴ f₂, где

f₂ – фронтальная проекция фронтали.

Следовательно, если прямая перпендикулярна к плоскости, то её проекции перпендикулярны к одноимённым проекциям одноимённых линий уровня, то есть если n_┴ Σ (h∩f), то n_1┴ h₁ и n_2┴ f₂.

Пусть требуется из точки K(K₁, K₂)восстановить перпендикуляр к плоскости Σ (a||b)(рис. 3.26, а).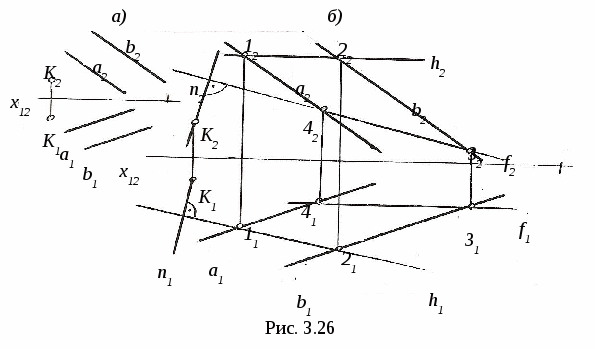

На рис. 3.26, б показано построение такого перпендикуляра .

В плоскости Σ проведены горизонталь h (h₁, h₂) и фронталь f (f₁, f₂).

Через точку K₁ проведена n_1┴ h₁ и через точку K₂проведена n_2┴ f₂.

3.5.3. Перпендикулярные плоскости. Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую линию, перпендикулярную другой. Поэтому при проведении плоскости, перпендикулярной к другой плоскости, сначала строят прямую, перпендикулярную к плоскости, и затем заключают её в какую-либо плоскость.

На рис. 3.27 через точку B проведена плоскость T(m∩n) перпендикулярно Σ (a||b).

Для этого в плоскости Σ (a||b) построены горизонталь h (h₁, h₂) и фронталь f (f₁, f₂).

Затем через точку B проводим n_┴Σ, то есть n_1┴ h₁, n_2┴ f₂. Прямую m (m₁, m₂) через точку B (B₁ , B₂) проводим произвольно.

Построенная плоскость T (m∩n) будет перпендикулярна Σ.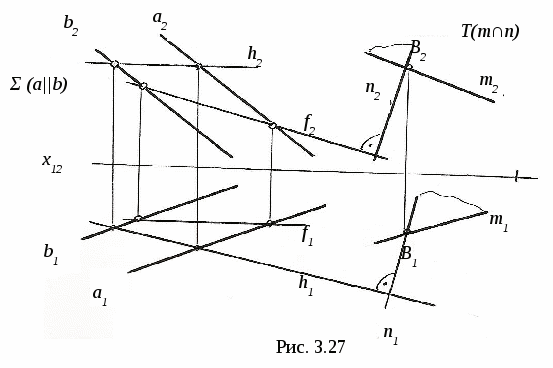



4. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
4.1. Образование и виды аксонометрических проекций
Проекция предмета вместе с заданной системой координат на одну плоскость называется аксонометрической проекцией или аксонометрией. Плоскость проекций в этом случае называется аксонометрической. Наиболее часто применяется параллельное аксонометрическое проецироввание.

Образование аксонометрической проекции рассмотрим на примере построения аксонометрии точки В, отнесённой к натуральной системе координат xyz(рис. 4.1). Здесь П_А – аксонометрическая плоскость проекций, s– направление проецирующих лучей, В_А – аксонометрическая проекция точки В; x_A, y_A, z_A – аксонометрические проекции осей координат x, y, z; эти проекции также называются аксонометрическими координатными осями.

При аксонометрическом проецировании происходит искажение линейных размеров проецируемых объектов, которое характеризуется коэффициентами искажения по направлениям вдоль координатных осей. Коэффициент искажения по оси х определяется отношением длины аксонометрической проекции отрезка, отложенного вдоль этой оси, к натуральной величине этого отрезка: к=О_АЕ_А /ОЕ. Аналогично определяются коэффициенты искажения по осям y и z – соответственно величины m и n.




z_B


x_В


y_В


В зависимости от положения аксонометрической плоскости проекций П_А относительно координатной системы xyzаксонометрические оси x_A, y_A, z_A могут занимать различные положения, а коэффициенты искажения принимают различные значения. Аксонометрические проекции, в которых k = m = n , называются изометрическими; если k = n ≠ m – диметрическими; если k ≠ m ≠ n – триметрическими.

Аксонометрические проекции также различают в зависимости от угла наклона проецирующих лучей sк аксонометрической плоскости проекций П_А. Если sП_А , аксонометрическая проекция называется прямоугольной; если проецирующие лучи не перпендикулярны аксонометрической плоскости, аксонометрическая проекция называется косоугольной.

Аксонометрические проекции, рекомендуемые к применению при выполнении чертежей, включены в Государственный стандарт ГОСТ 3.317-69 «Аксонометрические проекции» Единой системы конструктрской документации. Далее рассмотрим эти проекции подробнее.
4.2. Прямоугольные аксонометрические проекции
4.2.1. Прямоугольная изометрическая проекция.В данной проекции k = m = n = 0,82. Для упрощения построений принимают k = m = n = 1, то есть масштаб при откладывании координат по всем трём аксонометрическим осям равен 1:1. Расположение аксонометрических осей показано на рис. 4.2.
С целью упрощения на этом и последующих рисунках подстрочный индекс «А» при обозначении аксонометрических проекций геометрических объектов (точек, прямых, осей координат) опущен. Такое упрощение применяется и в другой литературе, в том числе в учебном пособии «Рабочая тетрадь по техническому рисунку в аксонометрии», которое используется при проведении практических занятий по дисциплине «Технический рисунок».

Для построения в прямоугольной изометрии аксонометрической проекции точки В по её координатам x_В, y_В, z_B(рис. 4.1) вдоль оси Oх (рис. 4.2) откладываем отрезок, равный x_В. Из полученной точки В_Хпараллельно оси Oy проводим отрезок длиной y_Ви получаем точку В₁. Точка В₁ (на рис. 4.1 ей соответствует точка В_1А)называется вторичной проекцией точки В. Далее, проведя через точку В₁ отрезок, равный z_В параллельно оси Oz, получим аксонометрическую проекцию точки В. Ломаная линия OВ_ХВ₁В называется трёхзвенной координатной линией.

Для построения аксонометрической проекции отрезка прямой необходимо построить проекции двух точек концов отрезка с помощью трёхзвенной координатной линии и соединить построенные точки прямой линией.

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 4.3), причём малая ось эллипса совпадает с направлением оси координатной системы, отсутствующей в данной плоскости.

Так, если окружность расположена в плоскости хOy, то малая ось эллипса параллельна оси Oz, а большая перпендикулярна ей. При k = m = n = 1 большая ось 2a=1,22d, малая ось 2b = 0,71d, где d – диаметр окружности.

На рис. 4.3 эллипсы построены по восьми точкам.

На рис. 4.4 показано построение эллипса по большой оси AB (2a = 1,22d) и малой оси CD (2b = 0,71d). Из точки O проведены две концентрические окружности. Большую из них делят на несколько частей. Через точки деления и центр O проводят радиусы, которые делят также вторую окружность.


1

3

2

b

b

a

a

0

1

3

2

a

a

b

b
Затем через точки деления проводят прямые, параллельные осям AB и CD, точки пересечения которых расположены на эллипсе.