Главная страница
Навигация по странице:

  • актуальной

  • противоречие

  • проблема

  • Объёктом исследования

  • Методы исследования

  • Работа состоит

  • 2.Методика формирования первоначальных вычислительных навыков

    		•

    Курсовая работа по теме Формирование вычислительных навыков у младших школьников. КР Смолянской Д.. Н. Б. Истомина (Гармония), Аргинская И. И., Е. П. Бененсон, Л. С. Итина (Л. В. Занкова)


    Скачать 98.82 Kb.
    НазваниеН. Б. Истомина (Гармония), Аргинская И. И., Е. П. Бененсон, Л. С. Итина (Л. В. Занкова)
    АнкорКурсовая работа по теме Формирование вычислительных навыков у младших школьников
    Дата01.01.2023
    Размер98.82 Kb.
    Формат файлаdocx
    Имя файлаКР Смолянской Д..docx
    ТипДокументы
    #870375
    страница1 из 4
      1   2   3   4

    Введение

    Одной из важнейших задач обучения математике младших школьников является формирование у них вычислительной культуры, основу которой составляет осознанное и прочное усвоение приемов сложения и вычитания также умножения и деления многозначных чисел, а так же их сознательное использование. Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, является фундаментом изучения математики и других учебных дисциплин.

    Проблема формирования у учащихся вычислительной культуры всегда привлекала особое внимание психологов, методистов, учителей. В методике математики известны исследования Е.С. Дубинчук, А.А. Столяра, С.С. Минаевой, Н.Л. Стефановой, Я.Ф. Чекмарева, М.А. Бантовой, М.И. Моро, Н.Б. Истоминой, С.Е. Царевой и др.

    Глубоко и всесторонне вопросы совершенствования устных и письменных вычислений учащихся исследовались лишь в 60-70 гг. ХХ века. Исследования последующих лет посвящены преимущественно разработке качеств вычислительных навыков (М.А. Бантова), рационализации вычислительных приемов (М.И. Моро, С.В. Степанова и др.), дифференциации и индивидуализации процесса формирования вычислительных умений и навыков (Т.И.Фаддейчева).

    Большой вклад в развитие вычислительной культуры в содержательно-методическом аспекте внесли авторы учебников математики разных УМК: М.И.Моро, С.В. Степанова, С.И.Волкова. (Школа Росси), Г.В. Дорофеев, Т.Н. Миракова (Перспектива), Л.Г. Петерсон (Школа 2000), Т.Е. Демидова, С.А. Козлова, А.П. Тонких. (Школа 2100), А.Л. Чекин, О.А. Захарова, Е.П. Юдина ( Перспективная начальная школа), Е.Э.Кочурина, В.Н.Рудницкая, О.А.Рыдзе (Начальная школа XXI века), Н.Б. Истомина (Гармония), Аргинская И.И., Е.П.Бененсон, Л.С.Итина (Л.В. Занкова).

    Каждое из этих исследований внесло определенный вклад в разработку и совершенствование той методической системы, которая использовалась в практике обучения, и нашло отражение в учебниках математики.

    Действующие на сегодняшний день программы по математике обеспечивают достаточный уровень формирования вычислительных навыков школьников. Изучение вычислительного приема происходит после того, как школьники усвоят его теоретическую основу (определения арифметических действий, свойства действий и следствия, вытекающие из них). Причем в каждом конкретном случае учащиеся осознают сам факт использования соответствующих теоретических положений, лежащих в основе вычислительного приема, конструируют различные приемы для одного случая вычислений, используя различные теоретические положения. В начальном курсе математики предусмотрен такой порядок введения вычислительных приемов, при котором постепенно вводятся приемы, включающие большее число операций, а приемы, усвоенные ранее, включаются в новые в качестве основных операций.

    Переориентация методической системы на приоритет развивающей функции по отношению к образовательной, характеризующейся изменением характера деятельности учащихся, личностно-ориентированным подходом к обучению, несколько ослабила внимание к развитию и закреплению вычислительных навыков у учащихся.

    Учебники математики ориентированы на развитие общих вычислительных навыков, и учитель может легко обучить алгоритмам вычислений.

    Отмечается ухудшение качества вычислений учащихся, обучающихся и по обычным, и по развивающим учебникам. Особенно пострадала культура устного счета. «Стремление учителей изменить ситуацию приводит к тому, что одни учителя используют в работе два учебника: один выполняет развивающие функции, другой (традиционный) — нацелен на формирование вычислительных умений и навыков. Другие учителя увеличивают объем домашних заданий. Это приводит к перегрузкам школьников, провоцирует стрессовые ситуации, снижает интерес к математике». Таким образом, развитие вычислительной культуры младших школьников является для начальной школы актуальной проблемой.

    Многообразие УМК предлагает учителю начальных классов большой арсенал авторских подходов и приёмов вычислений. Это своего рода современная школа совершенствования методического уровня учителей начальных классов в аспекте развития вычислительной культуры младших школьников. Однако продолжает существовать противоречие между представленными в учебниках математики разных УМК содержательно-методическими условиями и уровнем развития вычислительной культуры младших школьников.

    Возникает проблема: как обеспечить формирование и развитие вычислительной культуры младших школьников в современных содержательно-методических условиях её становления.

    Объёктом исследования является процесс усвоения младшими школьниками начального курса математики.

    Предмет исследования: формирование вычислительной культуры младших школьников.

    Цель исследования: изучить процесс формирования вычислительной культуры у младших школьников и выявить проблемы их развития.

    Задачи:

    • Изучить требования ФГОС НОО в аспекте формирования вычислительной культуры младших школьников;

    • Изучить методику формирования первоначальных вычислительных навыков;

    • Исследовать внутрипредметные связи в аспекте развития вычислительной культуры младших школьников;

    • Изучить рациональные приемы формирования вычислительных навыков у младших школьников.

    Методы исследования: анализ научной, методической, периодической литературы по теме исследования, анализ базовых понятий исследования; изучение, анализ и обобщение передового опыта, наблюдение, беседа, самооценка.

    Работа состоит из введения, пяти параграфов, заключения, списка литературы и приложений.

    1.Требования ФГОС НОО в аспекте формирования вычислительной культуры младших школьников

    Современное изменение системы школьного образования, в том числе начального, связано с введением Федерального государственного образовательного стандарта (ФГОС) начального общего образования. Начальное обучение математики закладывают основы для формирования приёмов умственной деятельности: школьники учатся проводить анализ, сравнение, классификацию объектов, устанавливать причинно-следственные связи, закономерности, выстраивать логические цепочки рассуждений. Изучая математику, они усваивают определённые обобщенные знания и способы действий. Универсальные математические способы познания способствуют целостному восприятию мира, позволяют выстраивать модели его отдельных процессов и явлений, а также являются основой формирования универсальных учебных действий. УУД обеспечивают усвоение предметных знаний и интеллектуальное развитие учащихся, формируют способность к самостоятельному поиску и усвоению новой информации, новых знаний и способов действий, что составляет основу умения учится. Достижение личностных и метапредметных результатов рассматривается наряду с предметными.

    В результате изучения математики учащиеся должны:

    • выполнять письменно действия с многозначными числа ми (сложение, вычитание, умножение и деление на однозначное, двузначное числа в пределах 10 000) с использованием таблиц сложения и умножения чисел, алгоритмов письменных арифметических действий (в том числе деления с остатком);

    • выполнять устно сложение, вычитание, умножение и деление однозначных, двузначных и трехзначных чисел в случаях, сводимых к действиям в пределах 100 (в том числе с нулем и числом 1);

    • выделять неизвестный компонент арифметического действия и находить его значение;

    • вычислять значение числового выражения (содержащего 2—3 арифметических действия, со скобками и без скобок). Выпускник получит возможность научиться:

    • выполнять действия с величинами;

    • использовать свойства арифметических действий для удобства вычислений;

    • проводить проверку правильности вычислений (с помощью обратного действия, прикидки и оценки результата действия).

    Напрямую с вычислительной культурой связана большая часть предметных результатов обучения математике: «использование приобретённых математических знаний для описания и объяснения окружающих предметов, процессов, явлений, а также для оценки их количественных отношений»; «овладение основами логического и алгоритмического мышления, математической речи, основами счёта, измерения, прикидки результата и его оценки, наглядного представления данных в разной форме (таблицы, схемы, диаграммы), записи и выполнения алгоритмов»; «приобретение начального опыта применения математических знаний для решения учебно-познавательных и учебно-практических задач»; «умения выполнять устно и письменно арифметические действия с числами и числовыми выражениями, решать текстовые задачи, выполнять и строить алгоритмы и стратегии в игре, . работать с таблицами, схемами, графиками и диаграммами, цепочками, представлять, анализировать и интерпретировать данные».

    Формирование вычислительной культуры младших школьников обеспечивает достижение личностных, метапредметных, предметных (математических) результатов начального образования и вносит свой вклад в математическую культуру учащихся, формирующуюся в рамках культуры достоинства.
    2.Методика формирования первоначальных вычислительных навыков

    Формирование вычислительных навыков остается одной из главных задач обучения математики, так как вычислительные навыки необходимы как в практической жизни человека, так и в учении. Эти навыки должны формироваться осознано и прочно, так как на их базе строится весь начальный курс обучения математике, предусматривает формирование вычислительных навыков на основе сознательного использования приемов вычислений.

    Невысокий уровень вычислительных навыков сказывается на качестве обучения и уровне математических знаний учащихся в целом. Именно поэтому впервые годы обучения закладываются основные приемы вычислительных навыков, которые активируют мыслительную деятельность учеников, развивают у детей память, повышают внимание и быстроту реакции, например, прием округления при сложении и вычитание в пределах второго десятка с переходом через десяток.

    Вычислительные навыки успешно формируются у учащихся при создании в учебном процессе определенных условий. Процесс овладения вычислительными навыками довольно сложен: сначала ученики должны усвоить тот или иной вычислительный прием, а затем в результате тренировки научится достаточно быстро выполнять вычисления, а в отношении табличных случаев – запомнить результаты наизусть.

    Все вычислительные приемы строятся на той или иной теоретической основе, причем в каждом случае учащиеся осознают сам факт использования соответствующих теоретических приемов. Это – реальная предпосылка овладения учащимися осознанными вычислительными навыками.

    Вычислительные навыки характеризуются свёрнутым в значительной мере автоматизированным выполнением действия, с пропуском промежуточных операций, когда контроль переносится на конечный результат.

    В начальном курсе математики учащиеся должны усвоить на уровне навыка:

    Усвоение этих таблиц должно быть доведено до автоматизма.

    Можно выделить 3 подхода к формированию вычислительных навыков:

    1. Можно просто выучить таблицы сложения, умножения и соответствующие случаи деления и вычитания; закрепить их в процессе решения примеров, так как сами предоставляют собой таблицу, только в разбивку. Познавательная деятельность учащихся характеризуется активной работой памяти и напряжением произвольного внимания;

    2. При втором подходе учащиеся знакомятся с различными вычислительными приёмами, самостоятельно составляют таблицы и непроизвольно запоминают их в процессе выполнения различных вычислительных упражнений;

    3. Третий подход отличается от второго тем, что в определенный момент, после использования предметных действий и различных вычислительных приёмов, ученику даётся установка на запоминание. Усвоение вычислительных навыков предполагает осознанное составление таблиц и их непроизвольное запоминание в процессе специально организованной деятельности.

    Таблицы сложения и вычитания в пределах 10 можно условно разделить на 7 этапов:

    • Навык прибавления числа 1 (получение последующего числа), вычитания числа 1( получение предыдущего числа). Уже при изучении этих видов примеров применение счетных палочек недопустимо;

    7
    +
    1
    =
    8,
    6
    -
    1
    =
    5.




    • Умение прибавления, вычитания числа 2 (получение дважды последующего или предыдущего числа). Прибавление и вычитание происходит по частям;

    7
    +
    2
    =
    7
    +
    1
    +
    1
    =
    9;

    9
    -
    2
    =
    9
    -
    1
    -
    1
    =
    7;

    Очень важно, что бы дети присчитывали (+2) или отсчитывали (-2), но не пересчитывали. Это умение важно перевести в навык по средствам выполнения «прыжка» через 1 число.

    • Навык прибавления, вычитания числа 3 по частям:

      5
      +
      3
      =
      5
      +
      1
      +
      2
      =
      8;

      9
      -
      3
      =
      9
      -
      1
      -
      2
      =
      6;

    • Прибавление и вычитание 4 по частям:

    6
    +
    4
    =
    6
    +
    2
    +
    2
    =
    10;

    7
    -
    4
    =
    7
    -
    2
    -
    2
    =
    3;

    Переместительное свойство сложения:

    a
    +
    b
    =
    b
    +
    a;
























    4
    +
    6
    =
    6
    +
    4
    =
    6
    +
    2
    +
    2
    =
    10;

    • Умение прибавить 6,7,8- на основе переместительного свойства:

      4
      +
      6
      =
      6
      +
      4
      =
      6
      +
      2
      +
      2
      =
      8
      +
      2
      =
      10;

    • Умение вычитать 6,7,8 по частям.

    Контрольная работа проводится в 2 этапа и выполняется в течение двух дней: 1 этап - проверка навыка сложения и вычитания в пределах первого десятка, 2 этап - решение задач, неравенств и т.д.

    Табличные случаи сложения и вычитания учащихся должны усвоить на уровне навыка. Это сложный и длительный процесс, в котором выделяют 10 этапов:

    1. Устная и письменная нумерация чисел второго десятка:

    • Образование чисел второго десятка;

    • Десятичный состав чисел второго десятка;

    11
    =
    10
    +
    1,
    12
    =
    10
    +
    2,
    13
    =
    10
    +
    2.

    2.Графическое изображение чисел второго десятка:

    (1 десяток) 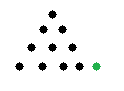( 11)

    Графическое изображение чисел второго десятка позволяет детям понять операции сложения и вычитания с опорой на десятичный состав чисел.

    3. Процесс формирования вычислительных навыков на десятичном составе чисел второго десятка.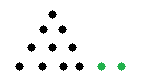

    + =

    10
    +
    2
    =
    12

    4.Сложение однозначных чисел с переходом через десяток:


    8
    +

    7

    =
    (8
    +
    2)
    +
    5
    =
    10
    +
    5
    =
    15




    2



    5

































    Прибавляем по частям: сначала первое слагаемое дополняем до 10, а затем прибавляем оставшиеся единицы.

    5. Вычитание однозначного числа из чисел второго десятка:

    13
    -

    7

    =
    (13
    -
    3)
    -
    4
    =
    10
    -
    4
    =
    6.




    3



    4

































    Вычитание по частям: сначала вычитаем все единицы, чтобы осталось только 10,затем вычитаем оставшиеся единицы.

    6. Изучение состава чисел второго десятка:

    1
    0



    1
    1



    1
    2



    1
    3



    1
    4



    1
    5



    1
    6



    1
    7



    1
    8

    1
    9



    2
    9



    3
    9



    4
    9



    5
    9



    6
    9



    7
    9



    8
    9



    9
    9

    2
    8



    3
    8



    4
    8



    5
    8



    6
    8



    7
    8



    8
    8



    9
    8









    3
    7



    4
    7



    5
    7



    6
    7



    7
    7



    8
    7



    9
    7


















    4
    6



    5
    6



    6
    6



    7
    6



    8
    6



    9
    6



























    5
    5



    6
    5



    7
    5



    8
    5



    9
    5




































    6
    4



    7
    4



    8
    4



    9
    4













































    7
    3



    8
    3



    9
    3






















































    8
    2



    9
    2































































    9
    1









































































    При изучении чисел их состав упрощается, количество пар чисел становится все меньше и меньше.

    7. Умение складывать и вычитать числа второго десятка переходит в навык. На основе знания состава чисел второго десятка все вычисления производятся автоматизировано в течении 4 секунд:

    8
    +
    9
    =
    17,
    15
    -
    6
    =
    9,
    5
    +
    8
    =
    13,
    14
    -
    6
    =
    8.

    8. Контрольно-оценочная деятельность по второму десятку:

    • Устные математические диктанты с применением сигнальных блокнотов;

    • Письменные математические диктанты 2 видов:

    - проверка знания состава чисел второго десятка (учитель называет первое слагаемое, учащиеся дополняют его в данном случае до 12, опираясь на состав числа 12):

    12
    8,
    6,
    4,
    9,
    7,
    и т.д.



    Нужно не забывать ставить точку на местах отсутствия ответов учеников.

    - проверка усвоения состава нескольких чисел второго десятка.

    8
    +
    4,
    14
    -
    6,
    11
    -
    3,
    6
    +7,
    9
    +
    6,
    16
    -
    7,
    8
    +
    9,
    и т.д.


    9. Итоговая форма контрольно-оценочной деятельности по окончанию изучения чисел второго десятка.
    I вариант



    II вариант

    №1
    письменный математический диктант
    №1
    решение задач



    №2
    решение задач
    №2
    письменный математический диктант




    Содержание диктанта единое. Примеры на сложение и вычитание с опорой на всех чисел второго десятка, однако, даны в разном порядке следования.

    На основе примерно половины пар состава чисел второго десятка формируются примеры на сложение и вычитание вперемешку.

    Представим фоновые предметные компетенции, на которых базируется навык сложения и вычитания в пределах второго десятка:

    • Обеспечивают формирование умений складывать и вычитать:

    1. Десятичный состав чисел второго десятка, переведенный в навык.

    2. Состав чисел первого десятка, переведенный в навык.

    • Обеспечивают навык сложения и вычитания чисел.

    3. Состав чисел второго десятка

    Вычислительный навык – это высокая степень овладения вычислительными приемами. Приобрести вычислительные навыки – значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро.

    Полноценный вычислительный навык характеризуется правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом, прочностью.

    Правильность – ученик правильно находит результат арифметического действия;

    Осознанность – ученик осознает, на основе каких знаний выбраны операции и установлен порядок их выполнения;

    Рациональность – ученик выбирает для данного случая более рациональный приём;

    Обобщенность – ученик может применить приём вычисления к большему числу случаев;

    Автоматизм – ученик выполняет и выделяет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операций. Высокая степень автоматизма должна быть достигнута по отношению к табличным случаям сложения и вычитания, умножения и деления.

    Прочность – ученик сохраняет сформированные вычислительные навыки на длительное время.

    Критерии по уровням сформированности вычислительного навыка представлены в приложении А.
      1   2   3   4

    написать администратору сайта