Математическое моделирование - Никишев. Н. Ульянова В. К. Никишев Математическое моделирование

• Название: Н. Ульянова В. К. Никишев Математическое моделирование
• Анкор: Математическое моделирование - Никишев.doc
• Дата: 01.04.2018
• Размер: 6.84 Mb.
• Имя файла: Математическое моделирование - Никишев.doc
• Тип: Документы; #17476
• страница: 1 из 6

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное

учреждение высшего профессионального образования

«Чувашский государственный университет имени И. Н. Ульянова»

В. К. Никишев

Математическое

моделирование

Лабораторный практикум


Чебоксары

2013
УДК 004.92(076.5)

ББК 3973.2-044.4я73

Н62

.

Никишев В. К.

Н62 Математическое моделирование: лабораторный практикум.

Чебоксары: Изд-во Чуваш. Ун-та, 2013. – 151 с.

Представлены примеры выполнения лабораторных работ по моделированию на языках программирования Delphi, VS 2010 ( VC#,VC++, VB.NET) и в среде моделирования SciLab (MatLab). Тематика лабораторных работ соответствует рабочей программе по математическому моделированию, которая составлена в соответствии со стандартом образования. Каждая работа содержит условие задачи, алгоритм в виде блок-схемы, программы на языках программирования VC#, VC++, DELPHI и результаты исследований. Задания для выполнения лабораторных работ представлены в конце лабораторного практикума.

Для бакалавров II-III, магистров и аспирантов технических факультетов, изучающих математическое моделирование с использованием современных языков.

Ответственный редактор канд. техн. наук, профессор В. К. Никишев
Утверждено Учебно-методическим советом университета

УДК 004/92(076/5)
ISBN 978-5-7677-1739-2 © Издательство Чувашского

Университета, 2013 © Никишев В. К., 2013
Предисловие

В настоящее время большое внимание уделяется вопросам моделирования различных систем с использованием современных языков программирования (Visual Basic, Delphi, VC#, VC++, VB.NET) и информационных программ, например, Excel, MathCad, MatLab, Maple, SciLab.

В отличии от программирования, где разрабатываются алгоритм и программа для решения какой-либо задачи для получения результата решения при заданных исходных данных, в моделировании разрабатываются алгоритм и программа для исследования систем, объектов или процессов. Необходимо помнить, что моделирование – это исследование систем, это вычислительный эксперимент. А исследование обычно проводится с учетом воздействия на модель, представленной в математической или иной формах, различных входных параметров или изменение различных коэффициентов, которые входят в уравнение модели. В результате проведения вычислительного эксперимента по полученным результатам можно сделать соответствующие выводы по устойчивости систем, точности систем, управлению объектов или в целом по работе какой-либо информационной системы при различных воздействиях на систему. Поэтому в отличие от простой программы необходимо разработать проект для исследования системы. Такой проект может иметь следующую структуру: получение результата моделирования при конкретных параметрах, при изменении параметров в определенных интервалах и получения так называемого среза результата при изменении исследуемого параметра в определенных интервалах.


Лабораторная работа 1. Методы исследования объектов, динамика которых описывается дифференциальными уравнениями с использованием языков программирования

Delphi,_VC++.NET,_VC._NET__Цель_занятия'>Delphi, VC++.NET, VC#. NET

Цель занятия:

1. Получить практические навыки исследования систем (объектов), динамика которых описывается дифференциальными уравнениями 1-го порядка.

2. Научиться разрабатывать алгоритм и программу с использованием языков программированияDelphi, VC++.NET, VC#.NET

3. Практически усвоить численные методы Эйлера и Рунге-Кутта для решения дифференциальных уравнений 1-го порядка.

Задачи занятия:

1. Разработка алгоритма в виде блок-схемы.

2. Построение графиков кривых y=f(x), ý = f(x) при параметрах a-const и var.

3. Анализ результатов исследований.

Модели объектов исследования

aӳ+bý + cy=f

Программа исследования

1. a,c,f - const, t – var ( t0 – tk, h= 0.1, 0.01)

2. a,f - const, t -var( t0 – tk, h= 0.1, 0.01), b- var

Пример 1

Условие задачи: cоставить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 1-го порядка методом Эйлера

5 ý + 3 y = 4/


Блок-схема алгоритма



Отчет по лабораторной работе


Рис.1. Форма 2. Автор Рис. 2. Форма 4. Условие


Рис. 3. Форма 1. Титульный лист
Форма для исследования объекта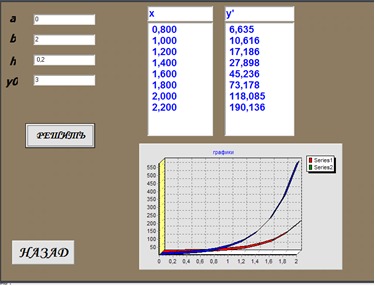




Рис. 4. Форма 3. Результаты исследования
Листинг программы ( язык программирования Delphi)

procedure TForm3.Button2Click(Sender: TObject); ( рис. 4).

var: x:real; i:integer;

function F(x,y:real):real;

begin

f:=5*x+(3*y)-4;

end;

begin

a:=StrToFloat(Edit1.text);

b:=StrToFloat(Edit2.text);

h:=StrToFloat(Edit3.text);

y1:=strtofloat(edit4.text); //шаг

memo1.lines.add(floattostr(x));

memo2.lines.add(floattostr(y));

x:=a;

Chart1.Series[0].clear; Chart1.Series[1].clear;

repeat

begin

y:=y1+h*f(x,y);

Chart1.Series[0].Add(y,FloatToStr(x),clRed);

Chart1.Series[1].Add(f(x,y),FloatToStr(x),clblue);

x:=x+h; y1:=y;

memo1.lines.add(floattostrf(x,fffixed,7,3));

memo2.lines.add(floattostrf(y,fffixed,7,3));

end;

until x>b;

end;
Листинг программы ( язык программирования VC++)
Исходное дифференциальное уравнение
ý - y - 2*sin(x) = 0;


Рис 5. Форма для условия задачи.
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {

this->Hide();

}

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

double f1,x, y1;

double h = Convert::ToDouble(textBox1->Text);

double b = Convert::ToDouble(textBox2->Text);

double y = Convert::ToDouble(textBox3->Text);

x = 0;

y1 = y;

chart1->Series[0]->Points->Clear();

chart1->Series[1]->Points->Clear();

do

{

f1 = y - 2*sin(x);

x = x+h;

y = y+f1*h;

chart1->Series[0]->Points->AddXY(x, y);

chart1->Series[1]->Points->AddXY(x,f1);

}

while (x<=b);

}};}};}

Рис 6. Форма для автора.


Рис 7. Форма для отображения результатов моделировния.

Язык программирования C#

private void button1_Click(object sender, EventArgs e)

{

double h = 0.01;

double y = 0;

double b = 2;

double x = 0;

double y1 = 4;

do

{

double f = y + 2*Math.Sin(x);

x = x + h;

y = y1 + f * h;

chart1.Series[0].Points.AddXY(x, y);

chart1.Series[1].Points.AddXY(x, f);

y1 = y;

}

while (x <= b);

}

// foreach (DataPoint p in chart1.Series[0].Points)

// {

// Вывожу Х в лог

// textBox1.AppendText("X=" + p.XValue.ToString());

// textBox1.AppendText(Environment.NewLine);

// listBox1.Items.Add("X=" + p.XValue.ToString());

// }

// Y является массивом, поэтому пробегаю по массиву

// foreach (DataPoint yp in chart1.Series[0].Points)

// {

//Вывожу Y

// textBox1.AppendText("Y=" + yp.ToString());

// textBox1.AppendText(Environment.NewLine);

// listBox1.AppendText("Y=" + yp.ToString());

// listBox1.AppendText(Environment.NewLine);

// listBox2.Items.Add("Y=" + yp.ToString());

// }

// }

private void chart1_Click(object sender, EventArgs e)

{

}

private void button2_Click_1(object sender, EventArgs e)

{

Close();

} }}

Пример 2.

Условия задачи: Исследовать объект, динамика которого представляется дифференциальным уравнением
ý - y - a*sin(x) = 0;
Цель занятия: получить практические навыки исследования систем (объектов), динамика которых описывается дифференциальными уравнениями 1-го порядка при изменении параметра «а»

Задачи занятия:

1. Разработка алгоритма в виде блок- схемы.

2. Построение графиков кривых y=f(x), ý = f(x) =y(x) при параметрах a-var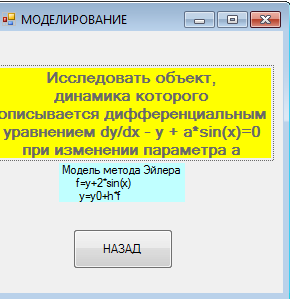





Рис 8. Титульный лист Рис. 9. Условия задачи

Рис 10. Автор программы




Рис. 11. Результаты исследования.

Листинг программы

private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {

this->Hide();

}

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

double f1,f2,x, y1;

double h = Convert::ToDouble(textBox1->Text);

double b = Convert::ToDouble(textBox2->Text);

double y2 = Convert::ToDouble(textBox3->Text);

double a = Convert::ToDouble(textBox4->Text);

double a1 = Convert::ToDouble(textBox5->Text);

x = 0;

// double y1 = y2;

int a3=a;

//for int i=0;i<=1;i++)

//{

chart1->Series[0]->Points->Clear();

chart1->Series[1]->Points->Clear();

chart1->Series[2]->Points->Clear();

chart2->Series[0]->Points->Clear();

chart2->Series[1]->Points->Clear();

chart2->Series[2]->Points->Clear();

//}

do

{

// for (int i=1;i<=5;i++)

// {

a3=a;

f1 = y2 - a3*sin(x);

// int i=0;

double y = y2+f1*h;

//int i=0;

chart1->Series[0]->Points->AddXY(x, y);

chart2->Series[0]->Points->AddXY(x,f1);

a3=a3+a1;

f1 = y2 - a3*sin(x);

y = y2+f1*h;

chart1->Series[1]->Points->AddXY(x,y);

chart2->Series[1]->Points->AddXY(x,f1);

a3=a3+a1;

f1 = y2 - a3*sin(x);

y = y2+f1*h;

chart1->Series[2]->Points->AddXY(x,y);

chart2->Series[2]->Points->AddXY(x,f1);

//y=y2;

x = x+h;

}

while (x<=b);

x=0;

}

private: System::Void chart2_Click(System::Object^ sender, System::EventArgs^ e) {

}

private: System::Void textBox1_TextChanged(System::Object^ sender, System::EventArgs^ e) {

}

};

}

Лабораторная работа 2

Методы исследования объектов, динамика которых описывается дифференциальными уравнениями 2-го поряда.

Цель занятия: Получить практические навыки исследования систем (объектов), динамика которых описывается дифференциальными уравнениями 2-го порядка.

Задачи занятия:

1. Разработка алгоритма в виде блок - схемы

2. Построение графиков кривых y=f(x), ý = f(x) =y(x) при параметрах a-const,

3. Анализ результатов исследований.
Пример исследования на языке программирования VC++


Рис. 12. Титульный лист


Рис 13. Автор программы Рис 14. Условие задачи



Лист 15. Результаты исследования

Листинг программы

private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {

this->Hide();

}

private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {

// int i = 1;

// int n = 100;

double f1,x,y11,y22;

double h = Convert::ToDouble(textBox1->Text);

double b = Convert::ToDouble(textBox2->Text);

double y1 = Convert::ToDouble(textBox3->Text);

double y2 = Convert::ToDouble(textBox4->Text);

x = 0;

chart1->Series[0]->Points->Clear();

chart1->Series[1]->Points->Clear();

do

{

// f1 = y - 2*sin(x);

x = x+h;

// y = y+f1*h;

y11=y1+h*y2;

y22=y2+h*(5-3*y2-4*y1);

//y = y1+h*(f1+(y - 2*x/y))/2;

chart1->Series[0]->Points->AddXY(x, y11);

chart1->Series[1]->Points->AddXY(x,y22);

y1=y11;

y2=y22;

}

while (x<=b);

}

private: System::Void Form5_Load(System::Object^ sender, System::EventArgs^ e) {

}};}
Пример исследования на языке Delphi

Условие задачи:cоставить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 2-го порядка методом Рунге-Кутта

y’’+a*x*y’-y=0,4.






Рис. 15. Титульный лист и условие задачи



Рис. 16. Задачи моделирования

Рис. 17. Результаты моделирования


Блок-схема алгоритма





Программа на Delphi

unit Unit2;

interface

var

Form2: TForm2;

implementation

uses Unit1,Unit4;

procedure TForm2.SpeedButton1Click(Sender: TObject);

begin

form4.Show;form2.Hide;

end;

procedure TForm2.SpeedButton2Click(Sender: TObject);

var

i,p :integer; // переменные, использующиеся в циклах

a : integer; // а - параметр а в нашем уравнении

h,t:real; // h - точность, t - шаг

n :integer; // число шагов

// x0,y0 :real; // начальные значения x и y

tn, tk : integer; // границы

x,y,kx1,kx2,kx3,kx4,ky1,ky2,ky3,ky4,dx,dy :array[1..10000] of real;

// x,y - значения x и y

// kx1-4,ky1-4 - переменные, принимающие участие в формуле Рунге-Кутта

//dx, dy - отрезки x и y решение уравнения по Рунге-Кутта

begin

a:=strtoint(edit1.Text);tn:=strtoint(edit2.Text);

tk:=strtoint(edit3.Text);h:=strtofloat(edit4.Text);

x[1]:=strtofloat(edit5.Text);y[1]:=strtofloat(edit6.Text);

n:=trunc((tk-tn)/h);

t:=tn;

chart1.SeriesList[0].Clear;chart2.SeriesList[0].Clear;

stringgrid1.RowCount:=n;

for i:= 1 to (n) do

begin

kx1[i]:=h*(-a*y[i]-6*x[i]);

kx2[i]:=h*(-a*y[i]-6*(x[i]+kx1[i]/2));

kx3[i]:=h*(-a*y[i]-6*(x[i]+kx2[i]/2));

kx4[i]:=h*(-a*y[i]-6*(x[i]+kx3[i]));

dx[i]:=1/6*(kx1[i]+2*kx2[i]+2*kx3[i]+kx4[i]);

x[i+1]:=x[i]+dx[i];

ky1[i]:=h*x[i];

ky2[i]:=h*(x[i]+ky1[i]/2);

ky3[i]:=h*(x[i]+ky2[i]/2);

ky4[i]:=h*(x[i]+ky3[i]);

dy[i]:=1/6*(ky1[i]+2*ky2[i]+2*ky3[i]+ky4[i]);

y[i+1]:=y[i]+dy[i];

t:=t+h;

stringgrid1.Cells[0,i]:=floattostr(t);

stringgrid1.Cells[1,i]:=floattostr(y[i]);

stringgrid1.Cells[2,i]:=floattostr(x[i]);

chart1.SeriesList[0].AddXY(t,y[i],'',clblue);

chart2.SeriesList[0].AddXY(t,x[i],'',clblue);

end;end;

procedure TForm2.FormCreate(Sender: TObject);

begin

stringgrid1.Cells[0,0]:='x';

stringgrid1.Cells[1,0]:='f(x)';

stringgrid1.Cells[2,0]:='f`(x)';end;end.

unit Unit5;

interface

var

Form5: TForm5;

implementation

uses Unit2, Unit4;

procedure TForm5.SpeedButton2Click(Sender: TObject);

var

i,p :integer; // переменные, использующиеся в циклах

a,a1,da : real; // а - параметр а в нашем уравнении

h,t:real; // h - точность, t - шаг

n,j :integer; // число шагов

// x0,y0 :real; // начальные значения x и y

tn, tk : integer; // границы

x,y,kx1,kx2,kx3,kx4,ky1,ky2,ky3,ky4,dx,dy :array[1..10000] of real;

// x,y - значения x и y на соотвествующем шаге

// kx1-4,ky1-4 - переменные опринимающие участие в формуле Рунге-Кутта

//dx, dy - отрезки x и y решение уравнения

begin

for j:= 0 to 5 do begin

chart1.SeriesList[j].Clear;chart2.SeriesList[j].Clear;

end;

a:=strtofloat(edit1.Text);a1:=strtofloat(edit7.Text);

da:=strtofloat(edit8.Text);

j:=0;a:=a-da;

repeat

tn:=strtoint(edit2.Text);tk:=strtoint(edit3.Text);

h:=strtofloat(edit4.Text);x[1]:=strtofloat(edit5.Text);

y[1]:=strtofloat(edit6.Text);n:=trunc((tk-tn)/h);

t:=tn;chart1.SeriesList[0].Clear;chart2.SeriesList[0].Clear;

for i:= 1 to (n) do

begin

kx1[i]:=h*(-a*y[i]-6*x[i]);

kx2[i]:=h*(-a*y[i]-6*(x[i]+kx1[i]/2));

kx3[i]:=h*(-a*y[i]-6*(x[i]+kx2[i]/2));

kx4[i]:=h*(-a*y[i]-6*(x[i]+kx3[i]));

dx[i]:=1/6*(kx1[i]+2*kx2[i]+2*kx3[i]+kx4[i]);

x[i+1]:=x[i]+dx[i]; ky1[i]:=h*x[i];

ky2[i]:=h*(x[i]+ky1[i]/2); ky3[i]:=h*(x[i]+ky2[i]/2);

ky4[i]:=h*(x[i]+ky3[i]);

dy[i]:=1/6*(ky1[i]+2*ky2[i]+2*ky3[i]+ky4[i]);

y[i+1]:=y[i]+dy[i]; t:=t+h;

chart1.SeriesList[j].AddXY(t,y[i],'',clblue);

chart2.SeriesList[j].AddXY(t,x[i],'',clblue);

end;

a:=a+da; j:=j+1;

until a > a1

end;

procedure TForm5.SpeedButton1Click(Sender: TObject);

begin

form4.show;form5.Hide;

end;end.
unit Unit6;

interface

var i,p :integer; // переменные, использующиеся в циклах

h,t:real; // h - точность, t - шаг

n :integer; // число шагов

// x0,y0 :real; // начальные значения x и y

tn, tk : integer; // границы

x,y,kx1,kx2,kx3,kx4,ky1,ky2,ky3,ky4,dx,dy: array[1..10000] of real;

// x,y - значения x и y на соответствующем шаге

// kx1-4,ky1-4 - переменные принимающие участие в формуле Рунге-Кутта

//dx, dy - отрезки x и y, из которых складывается решение уравнения по Рунге-Кутту

a: real; // a - parametr

begin

tn:=strtoint(edit2.Text);tk:=strtoint(edit3.Text);

h:=strtofloat(edit4.Text);x[1]:=strtofloat(edit5.Text);

y[1]:=strtofloat(edit6.Text);n:=trunc((tk-tn)/h);

t:=tn;

chart1.SeriesList[0].Clear;chart2.SeriesList[0].Clear;

a:=4;

for i:= 1 to (n) do

begin

kx1[i]:=h*(-a*y[i]-6*x[i]);

kx2[i]:=h*(-a*y[i]-6*(x[i]+kx1[i]/2));

kx3[i]:=h*(-a*y[i]-6*(x[i]+kx2[i]/2));

kx4[i]:=h*(-a*y[i]-6*(x[i]+kx3[i]));

dx[i]:=1/6*(kx1[i]+2*kx2[i]+2*kx3[i]+kx4[i]);

x[i+1]:=x[i]+dx[i]; ky1[i]:=h*x[i];

ky2[i]:=h*(x[i]+ky1[i]/2);

ky3[i]:=h*(x[i]+ky2[i]/2);

ky4[i]:=h*(x[i]+ky3[i]);

dy[i]:=1/6*(ky1[i]+2*ky2[i]+2*ky3[i]+ky4[i]);

y[i+1]:=y[i]+dy[i];

t:=t+h;

chart1.SeriesList[0].AddXY(t,y[i],'',clblue);

chart2.SeriesList[0].AddXY(t,x[i],'',clblue); end;end;
SciLab'>Лабораторная работа 3

Методы исследования объектов, динамика которых описывается дифференциальными уравнениями с использованием программы для моделирования

SciLab (MatLab)

Цель занятия:

1. Получить практические навыки исследования систем (объектов), динамика которых описывается дифференциальными уравнениями.

2. Научиться разрабатывать алгоритм и программу с среде моделирования SciLab ( MatLab).

3. Практически усвоить численные методы Эйлера для решения дифференциальных уравнений 1-го и 2-го порядков

Задачи занятия:

1. Разработка алгоритма в виде блок-схемы

2. Построение графиков кривых y(x), dy/dx при параметрах a-const и var.

3. Анализ результатов исследований.
Модели объектов исследования
aӳ+bý + cy=f

Программа исследования

1. a,c,f - const, t – var ( t0 – tk, h= 0.1, 0.01)

2. a,f - const, t -var( t0 – tk, h= 0.1, 0.01), b- var
Пример 1

Условие задачи: составить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 1 порядка методом Эйлера

ý + 4 ysin(t)-5.
программа

function yd=f(t, y),yd=5*t-4*y*sin(t),endfunction;

y0=5;t0=0;t=0:0.01:3;

y=ode(y0,t0,t,f);

plot(t,y)




Рис. 20. Результаты исследования
Пример 2

Условие задачи: составить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 1-го порядка методом Эйлера

ý + а* ysin(t)-5 , при изменении параметра на 4 значения.

N=4;

//disp(’Vvod N’);

//Цикл для ввода элементов в массиве y.

a=1;a1=2;

for i=1:N

function yd=f(t, y), yd=5*t-a*y*sin(t), endfunction;

y0=5;t0=0;t=0:0.01:3;

y=ode(y0,t0,t,f);

plot(t,y)

a=a+a1;

end

disp(y);





Рис. 21. Результаты исследования

Пример 3

Условие задачи: составить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 2-го порядка методом Эйлера

ӱ + 0.2*ý+ 4*y=2.
function dy=syst(t, y)dy=zeros(2,1);

dy(1)=y(2);

dy(2)=2-0.2*y(2)-4*y(1)

endfunction

y0=[0;0];t0=0;t=0:0.1:5;

y=ode(y0,t0,t,syst);

plot(t,y)

//end

//disp(y);



Рис. 21. Результаты исследования

Пример 4

Условия задачи. Исследовать объект, динамика которого описывается дифференциальным уравнением

ӱ + 0.2*ý+ 4*y=2

методом визуального моделирования

Исходное уравнение преобразуем к виду
Ӱ=2-0.2*ý-4*y



Рис. 22. Визуальная схема моделирования




Рис. 23. Результаты моделирования



Рис. 24. Визуальная схема моделирования



Рис. 25. Результаты моделирования

Пример 5

Условие задачи: составить алгоритм и проект моделирования объекта, динамика которого описывается дифференциальным уравнением 2-го порядка методом Эйлера

ӱ + 0.2*ý+ 4*y=2
N=4;

//disp(’Vvod N’);

//Цикл для ввода элементов в массиве y.

//a=1;a1=5;

//for i=1:N

function dy=syst(t, y)

dy=zeros(2,1);

dy(1)=y(2);

dy(2)=2-0.2*y(2)-4*y(1)

endfunction

y0=[0;0];t0=0;t=0:0.1:5;

y=ode(y0,t0,t,syst);

plot(t,y)

//end



Рис. 25. Результаты моделирования
Пример

Исследование в среде MatLab ( Simulink).

Условие задачи: составить алгоритм и проект:

моделирования объекта, динамика которого описывается

дифференциальным уравнением 2 порядка

y’’+axy’-y=0,4.





2.2

Рис 25. Визуальная схема и результаты исследования
Лабораторные работы для исследования физических, биологических и других систем

Пример исследования фыизических систем

Условие задачи.