Математическое моделирование - Никишев. Н. Ульянова В. К. Никишев Математическое моделирование

• Название: Н. Ульянова В. К. Никишев Математическое моделирование
• Анкор: Математическое моделирование - Никишев.doc
• Дата: 01.04.2018
• Размер: 6.84 Mb.
• Имя файла: Математическое моделирование - Никишев.doc
• Тип: Документы; #17476
• страница: 2 из 6

Тема: Свободное падение тел

Цель занятия: Изучить движение тел с высоты h при различных начальных условий: коэффициентов k1,k2, r

( радиуса шарика), плотности среды и формы тела.

Задачи занятия:

1. Получить зависимости h=f(t), v=f(t) при начальных значениях r,v0,h0,k1,k2.

2. Получить семейство графиков h=f(t,r), v=f(t,r).

3. Получить зависимость h=f(r), v=f(r) при t - const

Модель объекта


Параметры k1 и k2 зависят от свойств среды и геометрии тела. Например, для шарика k1 =6 r (формула Стокса), где - динамическая вязкость среды, r - радиус шарика. Так, для воздуха = 0,0182 Н*с*м-2 при t=20o C и давлении 1 атм. Соответственно для воды = 1,002 Н*с*м-2.. Для малых скоростей составляющей k1 можно пренебречь и Fс = k2*V2, где k2 = 0,5сS ; -плотность среды ; с- коэффициент лобового сопротивления, который зависит от формы тела. Так, для диска в форме прямоугольника с=1.11, для сферы с=1.33 и с=0.55 в зависимости от направления расположения сферы, для шара с=0.4, а для каплевидных тел с=0.045 с=0.1 в зависимости от направления тела.
.



Пример. Исследовать падение шарика радиуса R с высоты h

Задачи исследования:

1. Получить зависимости h=f(t), v=f(t) при начальных значениях r,v0,h0,k1,k2.

2. Получить семейство графиков h=f(t,r), v=f(t,r).

3. Получить зависимость h=f(r), v=f(r) при t - const

Исходные данные:

1. 
   Модель объекта падения, R - радиус шарика, h - высота падения, v0 - начальная скорость падения, k1 k2 - коэффициенты внешней среды.
   

2. 
   - площадь сечения тела, поперечного по отношению к потоку
   
3. 
   плотность шарика;
   
4. 
   – плотность воздуха.
   
5. 
   
   
6. 
   c = 0.4 – коэффициент лобового сопротивления шарика;
   

var

Form4: TForm4;

km,r,m,vo,ho,s,p,v,a,dv,da,c:double ;

h1,h2,cn,ck,dc,t,dt,y1,y2,dy1,dy2:double;

ind,k:integer;

arrt,arrv,arra,arrh:array[1..10000] of double;

implementation

uses Unit1, Unit5;

//описание функции

function ff(m,km,r,c,s,p,v:double):double;

begin

ff:=(m*9.8-6*km*Pi*r*v-0.5*c*s*p*v*v)/m;

end;

//Кнопка возврата к титульному листу

procedure TForm4.N3Click(Sender: TObject);

begin

form5.show;

for ind:=0 to 7 do

begin

form5.Chart1.SeriesList[ind].Clear;

form5.Chart2.SeriesList[ind].Clear;

end;

//Входные параметры

r:=strtofloat(edit1.Text);//радиус падующего тела

km:=strtofloat(edit2.text);//коэффициент вязкости

s:=strtofloat(edit3.Text);//площадь падующего тела

p:=strtofloat(edit4.Text);//плотность среды

ho:=strtofloat(edit5.Text);//начальная высота

vo:=strtofloat(edit6.Text);//начальная скорость

m:=strtofloat(edit7.Text);//масса падающего тела

c:=0.1;//коэффициент лобового сопротивления среды

k:=0;//номер графика

// 1

while c<=1.5 do

begin

ind:=0;

t:=0;dt:=0.1;

y1:=vo;

y2:=ff(m,km,r,c,s,p,vo);

while t<=10 do

begin

form5.Chart1.SeriesList[k].Add(y1,floattostr(t));

dy1:=dt*y2;

dy2:=dt*ff(m,km,r,c,s,p,y1);

y1:=y1+dy1;

y2:=y2+dy2;

t:=t+dt;

end;

c:=c+0.2;

k:=k+1;

end;

//2

k:=0;

t:=30;y1:=vo;y2:=ff(m,km,r,c,s,p,vo);

while t<=44 do

begin

c:=0.1;

while c<=2 do

begin

form5.Chart2.SeriesList[k].Add(y2,floattostr(c));

dy1:=dt*y2;

dy2:=dt*ff(m,km,r,c,s,p,y1);

y1:=y1+dy1;

y2:=y2+dy2;

c:=c+0.1;

end;

t:=t+2;

k:=k+1;

end;

end;

//Кнопка ввода данных

procedure TForm4.N1Click(Sender: TObject);

//Кнопка построения графика

procedure TForm4.N2Click(Sender: TObject);

begin

//очистка старых графиков

for ind:=0 to 7 do

begin

form4.Chart1.SeriesList[ind].Clear;

form4.Chart2.SeriesList[ind].Clear;

end;

//Входные параметры

r:=strtofloat(edit1.Text);//радиус падующего тела

km:=strtofloat(edit2.text);//коэффициент вязкости

s:=strtofloat(edit3.Text);//площадь падующего тела

p:=strtofloat(edit4.Text);//плотность среды

ho:=strtofloat(edit5.Text);//начальная высота

vo:=strtofloat(edit6.Text);//начальная скорость

m:=strtofloat(edit7.Text);//масса падающего тела

cn:=0.1;ck:=1.5;//интервал лобового сопротивления среды

dc:=(1.5-0.1)/7;//шаг изменения лобового сопротивления

k:=0;//номер графика

// цикл по лобовому сопротивлению

while cn<=ck do

begin

v:=vo;//первая производная расстояния по времени- начальная скорость

a:=1; //вторая производная расстояния по времени-ускорение

ind:=1;//счетчик записи данных в массивы

t:=0;//счетчик подчета времени падения тела

h1:=ho;//высота с которой падает тело

h2:=0; // тело лежит на земле

//цикл времени падения тела

while h1>=h2 do

begin

//запись в массивы полученных данных

arrh[ind]:=h1;//высота

arrv[ind]:=v;//скорость

arrt[ind]:=t;//время

//вывод графиков

form4.Chart1.SeriesList[k].Add(arrh[ind],floattostr(arrt[ind]));

form4.Chart2.SeriesList[k].Add(arrv[ind],floattostr(arrt[ind]));

// решение дифференциального уравнения методом Эйлера

dv:=0.01*a;

da:=0.01*ff(m,km,r,cn,s,p,a);

v:=v+dv;

a:=a+da;

h1:=h1-arrv[ind]*arrt[ind];//изменение высоты за время t

t:=t+0.01;//изменение времени

ind:=ind+1;

end;

//переход к следующему коэффициенту лобового сопротивления

// и соответсвенно к следующему графику

k:=k+1;

cn:=cn+dc;

end;

end;

procedure TForm4.N4Click(Sender: TObject);

begin

form4.Hide;

form5.hide;

form1.Show;

end;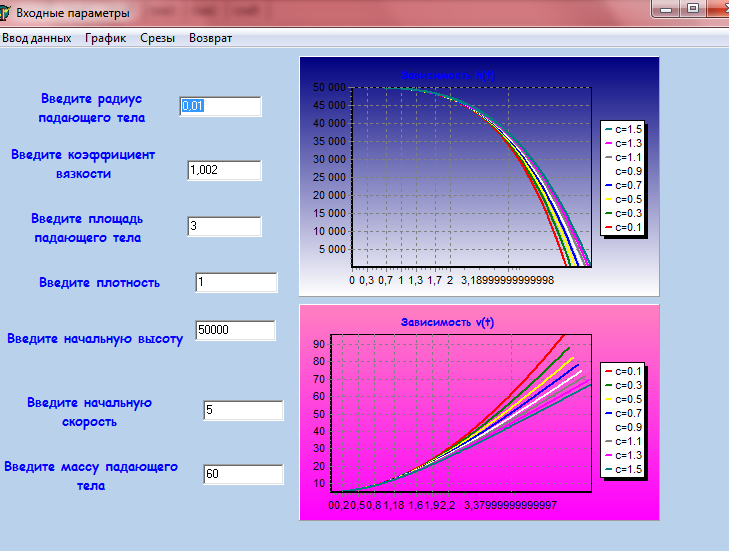





Пример2 . Исследовать падение шарика радиуса R с высоты h в среде MatLab

Задачи исследования:

1. Получить зависимости h=f(t), v=f(t) при начальных значениях r,v0,h0,k1,k2.

2. Получить семейство графиков h=f(t,r), v=f(t,r).

3. Получить зависимость h=f(r), v=f(r) при t - const

4. Исследовать в среде MatLab



Исследование системы с использованием программы MatLab.

Графики зависимостей v(t), h(t) для r=5mm c

помощью решателей ode15,ode45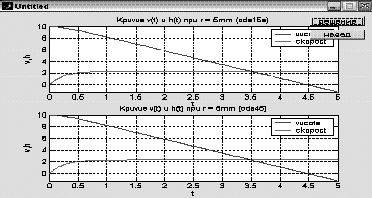


m-фа M-file f1.m:

function F1=pli(t,y)

mu=0.018; //динамическая вязкость воздуха

p1=800; //плотность шарика

p2=1.29; //плотность воздуха

c=0.4; //лобовое сопротивление шарика

g=9.8;

k=1000; //число разбиений

r=0.005; //радиус шарика

F1=[-y(2);9.8-9*mu/(r*r*p1*2)*y(2)-3*c*y(2)*y(2)*p2/(8*r*p1)];

m-файл для решения ДУ с помощью программы на языке программы MatLab M-file Sambo.m:

mu=0.018; //динамическая вязкость воздуха

p1=800; //плотность шарика

p2=1.29; //плотность воздуха

c=0.4; //коэффициент лобового сопротивления для шарика

g=9.8; //ускорение свободного падения

k=1000; //число разбиений

y(2)=0;y(1)=10;//начальные условия

x0=0;xk=5;//границы изменения времени

dx=(xk-x0)/k; //шаг интегрирования

r=0.005; //радиус шарика

x=x0;

subplot(2,1,1); //деление формы на 2 граф. окна

hold on; //обеспечивает продолжение вывода графиков в окно

for i=0:k-1

if y(1)<0 break,end;йл для решения ДУ с помощью решетелей

// вычисление коэффициентов для метода Рунге - Кутта

k11=-dx*y(2);k21=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*y(2)*y(2)*p2/(8*r*p1));

k12=-dx*(y(2)+k21/2);

k22=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k21/2)*(y(2)+k21/2)*p2/(8*r*p1)); k13=-dx*(y(2)+k22/2); k23=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k22/2)*(y(2)+k22/2)*p2/(8*r*p1));

k14=-dx*(y(2)+k23);k24=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k23)

*(y(2)+k23)*p2/(8*r*p1)); //расчёт разности

d1=(k11+2*k12+2*k13+k14)/6; d2=(k21+2*k22+2*k23+k24)/6;

//вычисление новых значений у1 и у2

y(11)=y(1)+d1; y(21)=y(2)+d2;

plot([x x+dx],[y(1) y(11)],’r’);plot([x x+dx],[y(2) y(21)],’b’),

x=x+dx; //новое значение х

y(1)=y(11); y(2)=y(21);

end;

grid on; //добавляет сетку к текущему графику

title(“Kpuvue v(t) u h(t) npu r = 5mm”); //установка на

графике титульной надписи

legend(“vucota”,’ckopoct’); //добавление к текущему графику xlabel('t');ylabel('v,h');

plot([0 5],[0 0],'k');axis tight;hold off; y(2)=0;y(1)=10;x0=0;xk=10;dx=(xk-x0)/k;

r0=0.002;rk=0.005;dr=(rk-r0)/3;

n=2;x=x0;r=r0;

subplot(2,1,2);hold on;

while r<=rk

for i=0:k-1

if y(1)<0 break,end;

k11=-dx*y(2);

k21=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*y(2)*y(2)*p2/(8*r*p1));

k12=-dx*(y(2)+k21/2);

k22=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k21/2)*(y(2)+k21/2)*p2/(8*r*p1)); k13=-dx*(y(2)+k22/2);

k23=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k22/2)*(y(2)+k22/2)*p2/(8*r*p1)); k14=-dx*(y(2)+k23);

k24=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k23)*(y(2)+k23)*p2/(8*r*p1));

d1=(k11+2*k12+2*k13+k14)/6; d2=(k21+2*k22+2*k23+k24)/6;

y(11)=y(1)+d1; y(21)=y(2)+d2;

plot([x x+dx],[y(1) y(11)],'r'); plot([x x+dx],[y(2) y(21)],'b');

x=x+dx; y(1)=y(11); y(2)=y(21); end;

x=x0; y(2)=0; y(1)=10;

r=r+dr; end;grid on;

title('Cemeuctvo v(t) u h(t): 2mm < r < 5mm');

legend('vucota','ckopoct');xlabel('t');ylabel('v,h');

plot([0 5],[0 0],'k');axis tight;hold off;

Графики зависимостей v(t),h(t) при r=5 mm и

семейство графиков для 2mm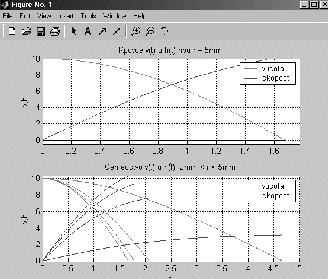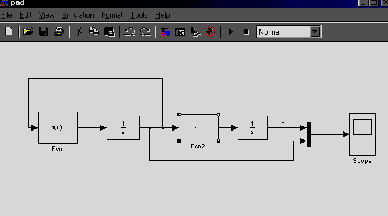



Simulink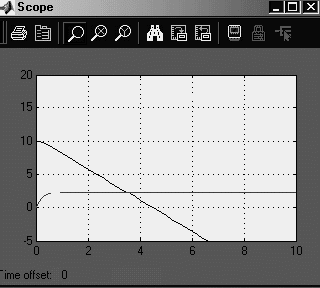

Пример3. Исследовать движение исследовательского зонда вертикально вверх с летящего самолета

Условие

Промоделировать движение исследовательского зонда, «выстреленного» вертикально вверх с летящего над землей самолета. В верхней точке траектории над зондом раскрывается парашют, и он плавно спускается на землю.

Входные параметры.

Математическая модель свободного падения тела - уравнение второго закона Ньютона с учетом двух сил, действующих на тело -силы тяжести и силы сопротивления среды. Движение является одномерным; проецируя силу, скорость и перемещение на ось, направленную вертикально вверх, получаем

Входные параметры модели:

¦ начальная высота тела;

¦ начальная скорость тела;

¦ величины, определяющие коэффициенты сопротивления среды

function FmO=fun(t,y)

tv=10;

a=100;

g=9,8

mn=10000;

mk=3000;

m=mn-a*t;

ifm>mk

else

m=mk end; mm=m; if t>=tv

p=0;

m=500; else

p=1000000;

m=mam; end;

FmO=[(p*cos(y(2))-cos(y(2))-g*sin(y(2)))/m;

((p*sin(y(2))+sin(y(2)))/m-

g*cos(y(2)))/y(l);-y(l)*cos(y(2))/10;y(l)*sin(y(2))/10];

Y0=[1000 pi/2 0 600];

[T,Y]=odel5s(@fun,[0 1000],Y0);

plot(Y(:53),Y(:,4),’g’);

hold on;

title(“zavisimost visoti ot vremeni”);

xlabel(fts’);

у1аЬеl(Ът’);

axis([0,5000,0,2000]);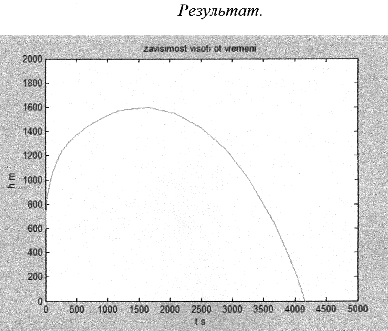




Пример. Исследование динамики объектов, брошенных под углом к горизонту.

Цель занятия:

Получить практические навыки исследования объектов, динамика которых описывается дифференциальными уравнениями 2-го порядка с использованием языков программирования :Delphi, VC++, VC# и информационных технологий MatLab.

Задачи занятия:

1. Разработка алгоритмов

2. Построение семейства кривых y(x), dy/dx(x) при параметрах a-const, a-var

3. Получение зависимостей y(a), dy/da при x-const

4. Анализ результатов исследований.

Задания для проведения лабораторной работы
Динамика объекта описывается системой дифференциальных уравнений

mdvx/dt = -Fccosq; =-Fcvx/v0

mdvy/dt = -m*g - Fcsinq,=-m*g - Fcvy/v0,
где Fc =k1V+ k2*V2 - линейная и квадратичная составляющая сопротивления воздуха.

2. Динамика объекта может представляется и алгебраическими уравнениями вида





var

Form1: TForm1;

xdp,ydp:integer;

x0,y0:integer;

alfa,veloc:real;

intravel:boolean=false;

// выводит результатскорости и направления

function rtostr(t:real):string;

var e:string;

begin

str(t:4:1,e);

result:=e;

end;

//выход

procedure TForm1.Button1Click(Sender: TObject);

begin

halt;

end;

// рисует стрелку , выводит скорость и направление

procedure drawmousec;

begin

with form1.paintbox1.Canvas do begin

pen.Mode:=pmXor;

moveto(x0,y0);

Lineto(xdp,ydp);

alfa:=pi/2-arctan((ydp-y0)/(xdp-x0));

Lineto(trunc(xdp+15*cos(-pi/2-alfa+pi/10)),trunc(ydp+15*sin(-pi/2-alfa+pi/10)));

moveto(xdp,ydp);

Lineto(trunc(xdp+15*cos(-pi/2-alfa-pi/10)),trunc(ydp+15*sin(-pi/2-alfa-pi/10)));

end;

alfa:=arctan((y0-ydp)/(xdp-x0));

form1.label1.Caption:='Направление: '+rtostr(alfa/pi*180)+' ; скорость: '+rtostr(veloc/50)+' ';

veloc:=sqrt(sqr(ydp/1-y0)+sqr(xdp/1-x0));

end;

// задает камень

procedure TForm1.PaintBox1Paint(Sender: TObject);

begin

if intravel then exit;

paintbox1.Canvas.pen.color:=clwhite;

paintbox1.Canvas.brush.color:=clwhite;

drawmousec;

end;

//координаты замка

procedure TForm1.FormCreate(Sender: TObject);

begin

xdp:=shape31.Left;

ydp:=shape31.Top;

x0:=shape25.left+shape25.width div 2;

y0:=shape25.top+shape25.height div 2;

end;

var dr:boolean=false;

//передвижение мышки вниз

procedure TForm1.PaintBox1MouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

if (x>x0)and(y
dr:=true;

drawmousec;

ydp:=y;xdp:=x;

drawmousec;

end;

end;

//передвижение мыши (стелки)

procedure TForm1.PaintBox1MouseMove(Sender: TObject; Shift: TShiftState; X,

Y: Integer);

begin

if (dr)and(x>x0)and(y
drawmousec;

ydp:=y;xdp:=x;

drawmousec;

end;

end;

// бросок

procedure TForm1.Button2Click(Sender: TObject);

const dt=0.01;

g=9.81;

var x,y,vx,vy,xo,yo:real;

bad:boolean;

r:integer;

begin

intravel:=true;

drawmousec;

vx:=veloc*cos(alfa);

vy:=veloc*sin(alfa);

x:=shape25.Left+shape25.height div 2;y:=shape25.Top+shape25.width div 2;r:=0;

repeat

xo:=x;yo:=y;

x:=x+vx*dt;y:=y-vy*dt;inc(r);

if r=10 then begin

sleep(1);

r:=0;

end;

vy:=vy-g*dt;

paintbox1.Canvas.pen.Mode:=pmCopy;

paintbox1.Canvas.pen.color:=clgreen;

paintbox1.Canvas.brush.color:=clgreen;

paintbox1.Canvas.Ellipse(trunc(xo-4),trunc(yo-4),trunc(xo+5),trunc(yo+5));

paintbox1.Canvas.pen.color:=clwhite;

paintbox1.Canvas.brush.color:=clwhite;

paintbox1.Canvas.Ellipse(trunc(x-3),trunc(y-3),trunc(x+4),trunc(y+4));

//trying to end the journey...

bad:=true;

if (y>y0/1)or(y<=0) then break;

if x>=shape15.Left then begin

if (x<=shape15.Left+shape15.width)and((y
(y>shape16.Top+shape16.height)) then break;

end;

if x>=shape22.Left then begin

if (y
(y>shape22.Top+shape22.height) then break else begin

bad:=false;

break;

end;

end;

until false;

intravel:=false;

if bad then begin

sleep(1000);

paintbox1.Repaint;

// drawmousec;

end else begin

shape32.Visible:=true;

label2.Visible:=true;

sleep(1000);

paintbox1.Repaint;

// drawmousec;

end;

end;

// изменение размеров замка

procedure TForm1.Shape32MouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

shape32.Visible:=false;

label2.Visible:=false;

end;

//вывод результатов

procedure TForm1.Label2MouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

shape32.Visible:=false;

label2.Visible:=false;

end;

// изменение координат замка

procedure TForm1.Splitter1CanResize(Sender: TObject; var NewSize: Integer;

var Accept: Boolean);

begin

accept:=false;

if newsize>=50 then begin

accept:=true;

end;

end;

// изменение координат замка

procedure TForm1.Splitter1Moved(Sender: TObject);

begin

halt;

end;

var s1d:boolean=false;

var s2d:boolean=false;

var s3d:boolean=false;

var s4d:boolean=false;

var s5d:boolean=false;

procedure TForm1.PaintBox2MouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s1d:=true;

end;

// изменение координатов замка мышью

procedure TForm1.PaintBox2MouseMove(Sender: TObject; Shift: TShiftState; X,

Y: Integer);

begin

if (s1d)and(shape15.Left+x>=50)and(shape15.Left+shape15.Width+x+50<=shape21.left) then begin

paintbox2.left:=paintbox2.left+x;

paintbox3.left:=paintbox3.left+x;

paintbox4.left:=paintbox4.left+x;

shape15.Left:=shape15.Left+x;

shape16.Left:=shape16.Left+x;

shape17.Left:=shape17.Left+x;

shape18.Left:=shape18.Left+x;

shape19.Left:=shape19.Left+x;

shape20.Left:=shape20.Left+x;

shape23.Left:=shape23.Left+x;

shape23.Width:=form1.width;

end;

end;

//передвижение мыши для изменения координат замка вверх

procedure TForm1.PaintBox2MouseUp(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s1d:=false;

end;

//передвижение мыши для изменения координат замка вниз

procedure TForm1.PaintBox3MouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s2d:=true;

end;

// изменение координатов замка мыщью

procedure TForm1.PaintBox3MouseMove(Sender: TObject; Shift: TShiftState; X,

Y: Integer);

begin

if (s2d)and(shape15.Width+x>=10)and(shape15.Left+shape15.Width+x+50<=shape21.left) then begin

shape15.Width:=shape15.Width+x;

shape16.Width:=shape16.Width+x;

paintbox3.left:=paintbox3.left+x;

shape17.width:=shape15.width+20;

shape17.left:=shape15.left-10;

paintbox4.width:=shape15.width+20;

paintbox4.left:=shape15.left-10;

shape18.width:=shape17.width div 5;

shape19.width:=shape17.width div 5;

shape18.left:=shape17.left;

shape19.left:=shape17.left+shape17.width div 5*2;

shape20.left:=shape17.left+shape17.width div 5*4;

shape20.width:=shape17.left+shape17.width-shape20.left;

end;

end;

//передвижение мыши для изменения координат замка вверх

procedure TForm1.PaintBox3MouseUp(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s2d:=false;

end;

//передвижение мыши для изменения координат замка вниз

procedure TForm1.PaintBox4MouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s3d:=true;

end;

//передвижение мыши для изменения координат замка вверх

procedure TForm1.PaintBox4MouseUp(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s3d:=false;

end;

//передвижение мыши для изменения координат

procedure TForm1.PaintBox4MouseMove(Sender: TObject; Shift: TShiftState; X,

Y: Integer);

begin

if (s3d)and(shape17.top+y>=100)and(shape16.Top+shape16.Height+y+20<=shape23.Top) then begin

shape17.top:=shape17.top+y;

shape18.top:=shape18.top+y;

shape19.top:=shape19.top+y;

shape16.top:=shape16.top+y;

shape20.top:=shape20.top+y;

shape15.top:=shape15.top+y;

paintbox4.top:=paintbox4.top+y;

paintbox3.top:=paintbox3.top+y;

paintbox2.top:=paintbox2.top+y;

shape15.height:=form1.height-shape15.top;

paintbox2.height:=form1.height-paintbox2.top;

paintbox3.height:=form1.height-paintbox3.top;

end;

end;

//передвижение мыши для изменения координат замка вниз

procedure TForm1.PaintBox5MouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s4d:=true;

end;

//передвижение мыши для изменения координат замка вверх

procedure TForm1.PaintBox5MouseUp(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s4d:=false;

end;

//передвижение мыши для изменения координат замка

procedure TForm1.PaintBox5MouseMove(Sender: TObject; Shift: TShiftState; X,

Y: Integer);

begin

if (s4d)and(shape22.top+y-10>=shape21.top)and(shape22.Top+shape22.Height+y+10<=shape23.Top) then begin

shape22.top:=shape22.top+y;

paintbox5.top:=paintbox5.top+y;

paintbox6.top:=paintbox6.top+y;

end;

end;

//передвижение мыши для изменения координат замка вниз

procedure TForm1.PaintBox6MouseDown(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s5d:=true;

end;

//передвижение мыши для изменения координат замка вверх

procedure TForm1.PaintBox6MouseUp(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

s5d:=false;

end;

procedure TForm1.PaintBox6MouseMove(Sender: TObject; Shift: TShiftState; X,

Y: Integer);

begin

if (s5d)and(shape22.height+y>=25)and(shape22.Top+shape22.Height+y+10<=shape23.Top) then begin

shape22.height:=shape22.height+y;

paintbox6.top:=paintbox6.top+y;

end;

end;
procedure TForm1.PaintBox1MouseUp(Sender: TObject; Button: TMouseButton;

Shift: TShiftState; X, Y: Integer);

begin

dr:=false;

end;
end.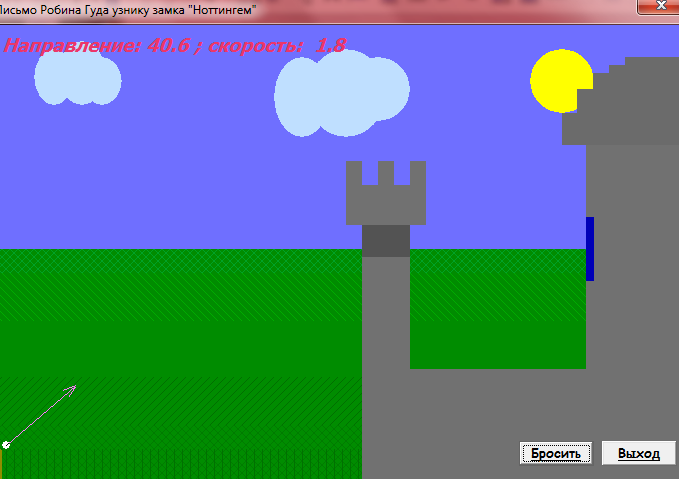





Пример модели движения небесных тел

По закону всемирного тяготения сила притяжения, действующая между двумя телами, пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними.


В этой формуле G=6,67*10-11 m3/(kг*с2) -гравитационная постоянная. В данной системе координат начало координат расположено на одном теле M. Уравнения, описывающие движение тела m в указанной системе координат, имеет вид


В проекциях на оси координат уравнение можно привести с следующей системе из 4-х дифференциальных уравнений



П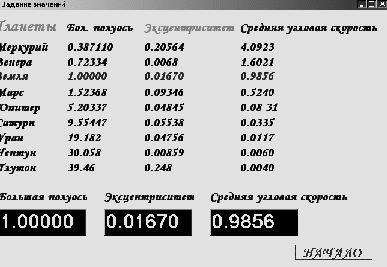ример 2. Исследовать выполнение второго закона Кеплера при движении различных планет.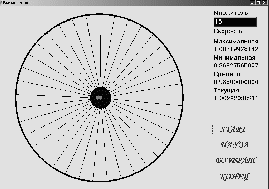



unit Unit2;

var

Form2: TForm2;

angle,j,k,kx,ky,ra,rb,e,x,y,va,vb,vc,a,t,t2,speed:real;

xc,yc,w,h,xf,n,cc,step:integer; flag:boolean;

implementation

uses Unit1, Unit3;

{$R *.dfm}

procedure TForm2.FormClose(Sender: TObject; var Action: TCloseAction);

begin

form1.close;

end;

procedure TForm2.BitBtn1Click(Sender: TObject);
var rrr:trect; aa,bb,cc:integer; s:string;

begin

// дано

val(form1.edit1.text,ra,cc);

if cc<>0 then ra:=1; val(form1.edit2.text,e,cc);

if cc<>0 then e:=0.0167; val(form1.edit3.text,vc,cc);

if cc<>0 then vc:=0.9856;

t:=360/vc; t2:=t/2; flag:=true;

// вычисляем

va:=vc*sqrt((1+e)/(1-e)); vb:=vc*sqrt((1-e)/(1+e));

a:=(va-vb)/t2; val(edit1.Text,step,cc);

if cc<>0 then step:=1; str(va:3:11,s);

label1.caption:=s; str(vb:3:11,s);

label2.caption:=s; str(vc:3:11,s);

label3.caption:=s; rb:=ra*sqrt(1-e*e);

// графика

w:=image1.Width; h:=image1.Height;

xc:=w div 2; yc:=h div 2;

kx:=ra/(xc-50); ky:=rb/(yc-50);

if kx>ky then k:=(xc-20)/ra else k:=(yc-20)/rb;

timer1.Enabled:=true;

aa:=round(ra*k); bb:=round(rb*k);

image1.Canvas.Brush.Color:=clnavy;

rrr:=rect(0,0,w,h); image1.Canvas.FillRect(rrr);

image1.Canvas.Brush.Color:=clwhite;

rrr:=rect(xc-aa,yc-bb,xc+aa,yc+bb);

image1.Canvas.Ellipse(rrr);

cc:=3; image1.Canvas.Brush.Color:=clnavy;

rrr:=rect(xc-aa+cc,yc-bb+cc,xc+aa-cc,yc+bb-cc);

image1.Canvas.Ellipse(rrr); xf:=round(ra*e*k);

cc:=30; image1.Canvas.Brush.Color:=clyellow;

rrr:=rect(xc+xf+cc,yc+cc,xc+xf-cc,yc-cc);

image1.Canvas.Ellipse(rrr);

cc:=6; image1.Canvas.Brush.Color:=clred;

rrr:=rect(xc-xf+cc,yc+cc,xc-xf-cc,yc-cc);

image1.Canvas.Ellipse(rrr);

rrr:=rect(xc+xf+cc,yc+cc,xc+xf-cc,yc-cc);

image1.Canvas.Ellipse(rrr);

angle:=0; n:=0; speed:=va; j:=pi/180;

end;

procedure TForm2.Timer1Timer(Sender: TObject);

var rrr:trect;s:string;i:integer;

begin

image1.Canvas.MoveTo(xc+xf,yc);

image1.Canvas.pen.Color:=clyellow;

ifangle<360 then image1.Canvas.

LineTo (xc+round(ra*cos(angle*j)*k),

(c-round(rb*sin(angle*j)*k)); for i:=1 to step do

begin

inc(n);

if angle<180 then speed:=speed-a else speed:=speed+a;

angle:=angle+speed; end;

str(speed:3:11,s); label4.Caption:=s;

if angle>=(360-a) then begin timer1.Enabled:=false; flag:=false; end;

cc:=6; image1.Canvas.Brush.Color:=clred;

rrr:=rect(xc-xf+cc,yc+cc,xc-xf-cc,yc-cc);

image1.Canvas.Ellipse(rrr);

rrr:=rect(xc+xf+cc,yc+cc,xc+xf-cc,yc-cc);

image1.Canvas.Ellipse(rrr);end;

procedure TForm2.BitBtn2Click(Sender: TObject);

begin

if flag then timer1.enabled:=not timer1.enabled;

end;

procedure TForm2.BitBtn3Click(Sender: TObject);

begin

form2.Hide; form1.Show;end;

procedure TForm2.BitBtn4Click(Sender: TObject);

begin

form2.Hide; form3.Show;

end;end.

2.4 Лабораторные работы по разработке имитационных моделей
Пример. Разработка информационной модели студента ( учащихся)

Цель занятия: Получить практические навыки в разработке информационных систем в среду БД Access , Excel

Задачи занятия:

2. Создать графическую модель студента с отображением диаграммы оценок по темам конкретной дисциплины

Информационная модель студента

Предметная информационная модель знаний студентов курса или факультета позволит получить следующие характеристики учебного процесса:

- качество обучения в целом по университету, факультету, курсу и успеваемость отдельных студентов;

-стабильность обучения по отдельным предметам, темам и дисциплинам;

- прогнозирование результатов обучения в предстоящем семестре;

-систематическое уточнение модели знаний студентов с использованием тестовых программ;

- разработка индивидуальных вопросов и задач на основе моделей знаний студентов;

- сравнительные оценки состояния учебного процесса как на факультете, так и по университету в целом.
Пример имитационной модели знаний студентов в среде Excel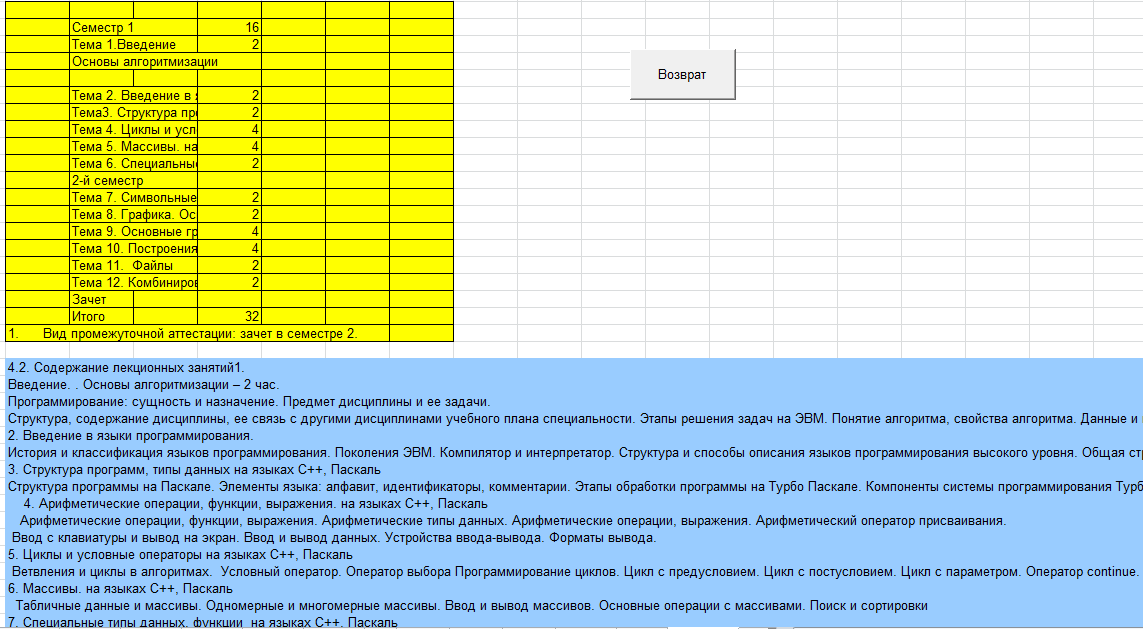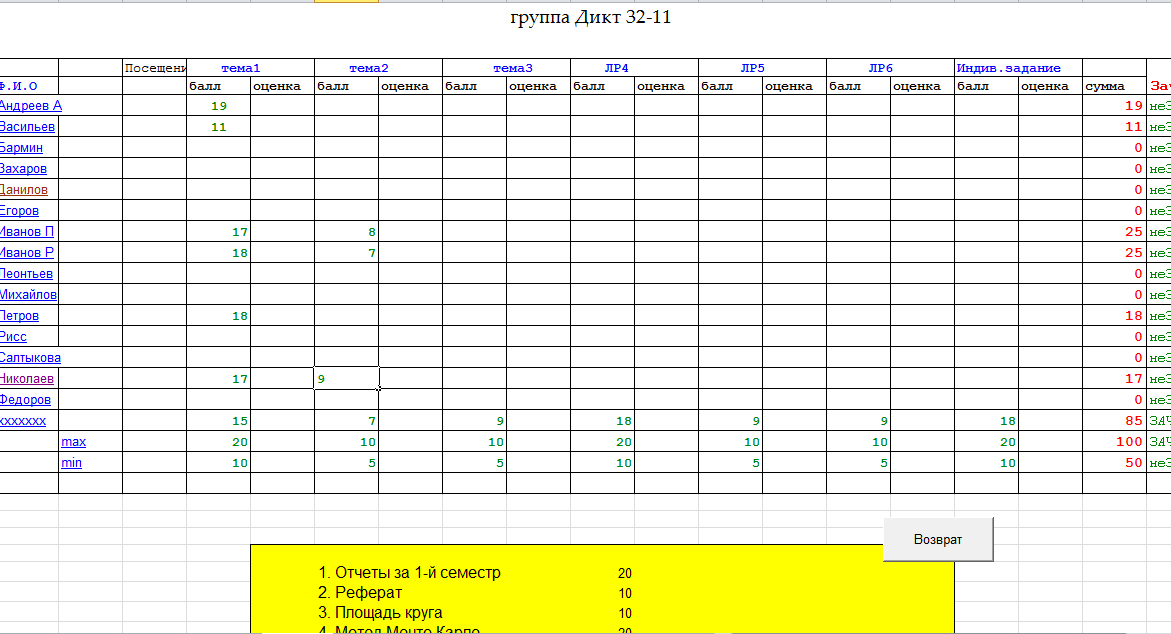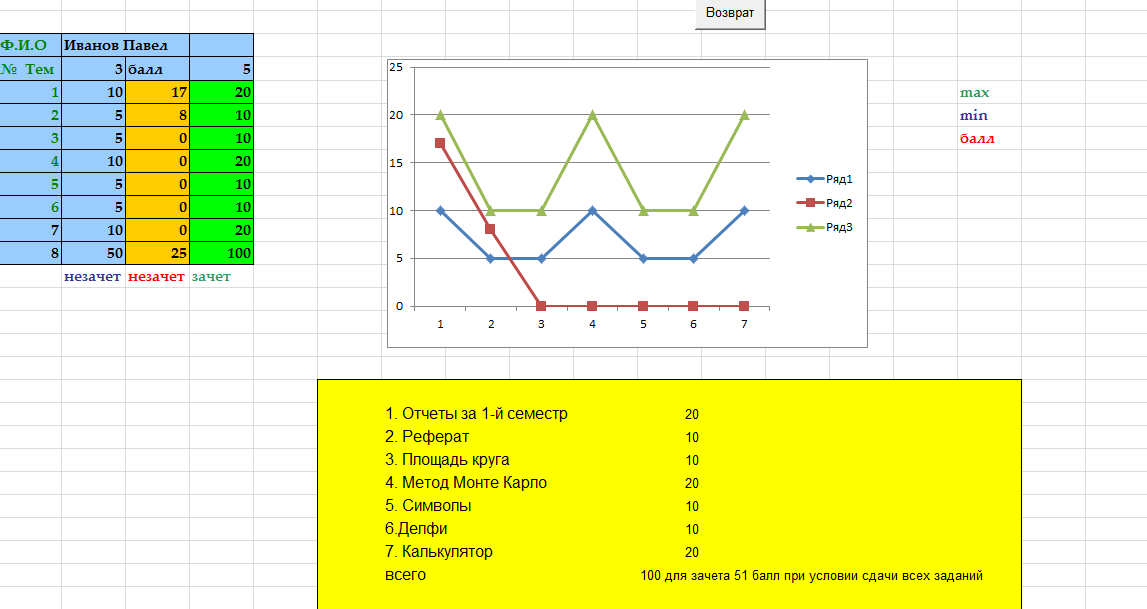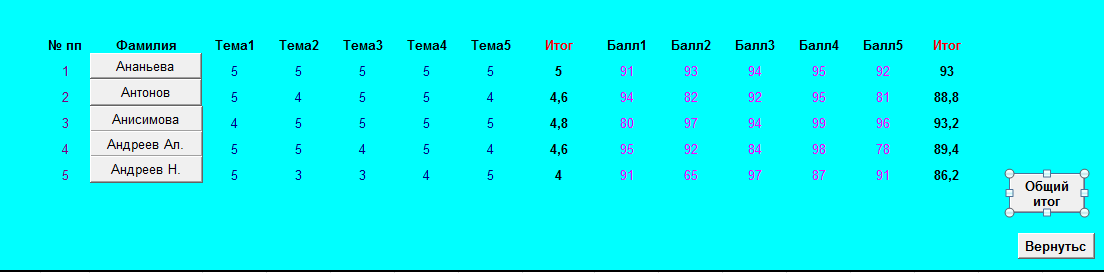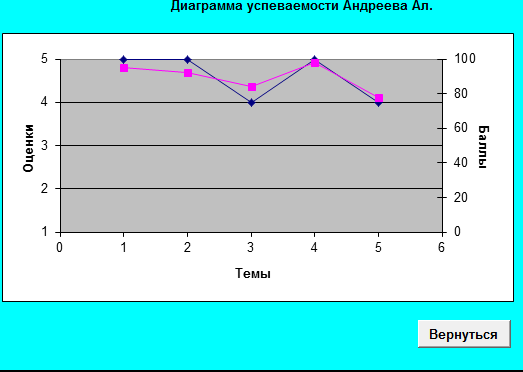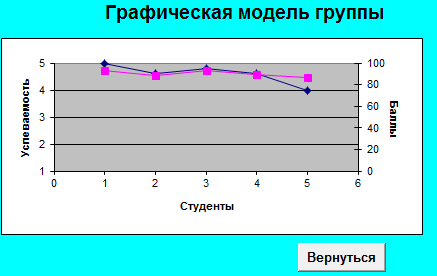






















Пример имитационной модели учащихся школы в среде Access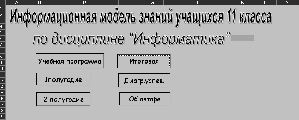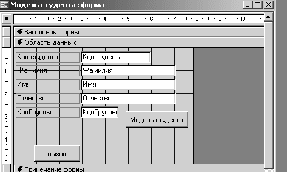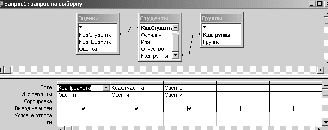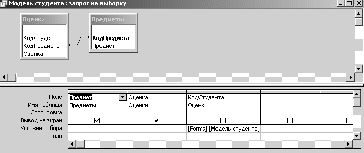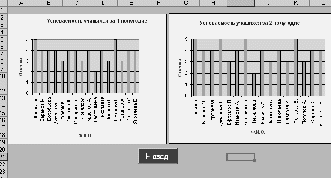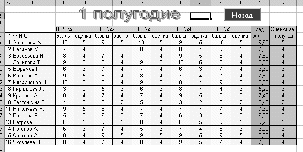
























2.5 Разработка моделей транспортных задач

Пример. «Размещения предприятий»
Исходные условия. Пусть в нескольких пунктах расположены предприятия, производящие некоторый продукт. В пунктах размещаются потребители готовой продукции с соответствующими потребностями . Затраты на производство единицы продукта в пункте равны , обьем производства в этом пункте равен , а затраты по транспортировке единицы продукта из i в j равны . Количество перевезенных продуктов из i в j составляет единиц. Уравнения модели:

1.(перевозится неотрицательное количество продукта);

2. (выпускаемое количество продукта не

больше возможного обьема производства и равно вывозимому количеству продукта);

3. , j=1,...,n (потребности потребителей),

(каждый пункт потребления получает столько, сколько ему требуется).

Конечная цель. Необходимо получить минимальные затраты на производство и на транспортировку продукции, т.е. обеспечить минимум функции





,

где - затраты на производство,

- затраты на транспортировку.

Целевая функция состоит из аналогичной целевой задачи. Однако, различие состоит в том, что здесь добавляются затраты на производство. Для однотипности подхода к решению этих двух моделей добавляется фиктивный пункт с характеристикой: потребность равна разности между возможным обьемом производства продукта и суммарной потребнос

,

где - затраты на производство,

- затраты на транспортировку.

Ц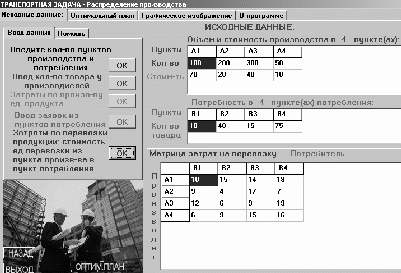елевая функция состоит из аналогичной целевой задачи. Однако, различие состоит в том, что здесь добавляются затраты на производство. Для однотипности подхода к решению этих двух моделей добавляется фиктивный пункт с характеристикой: потребность равна разности между возможным обьемом производства продукта и суммарной с


Пример Моделирование системы планирования

на основе метода сетевого графа

Задачи исследования

Необходимо спланировать временный график работ в соответствии с графом и вычислить критический путь выполнения всех работ

Исходные данные

Задание: Дана схема, нужно найти критический путь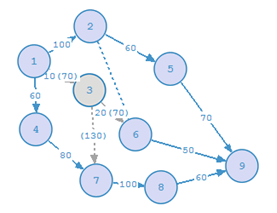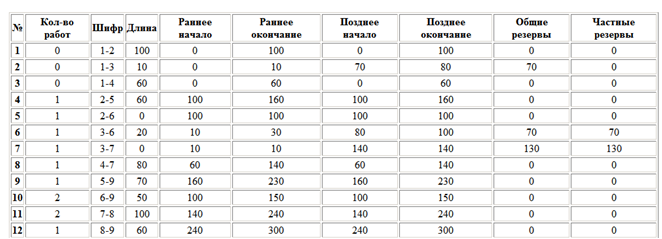







Пример. Планирование производства товаров на основе модели получения максимальной прибыли с использованием метода линейного программирования

Условие. Пусть предприятие производит столы и стулья. Расход ресурсов на их производство и прибыль от их реализации представлены в таблице. столы стулья объем ресурсов

Расход древесины

на изделие, м3 0,5 0,04 200

Расход труда(чел-час) 12 0,6 1800
Прибыль от реализации

единицы изделия , руб 180 20

Кроме того на производство 80 столов имеется заказ с министерством

Уравнения1-количество столов х2 - количество стульев

0,5 х1 + 0,04х2<=200

12x1 + 0,6x2 <=18000

x1+20x2 =max ( целевая функция)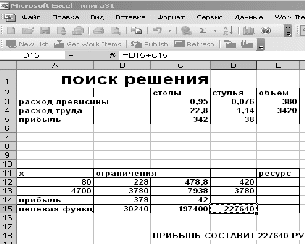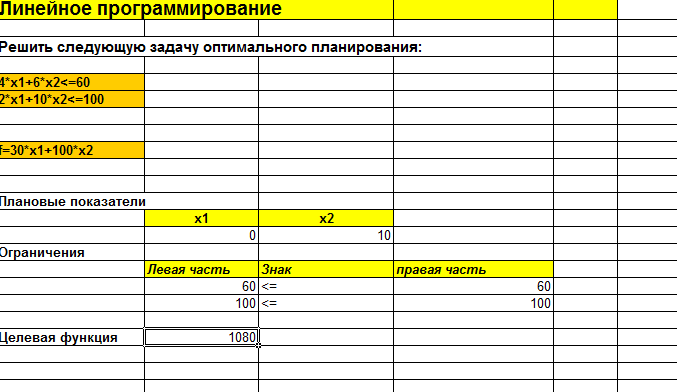















unit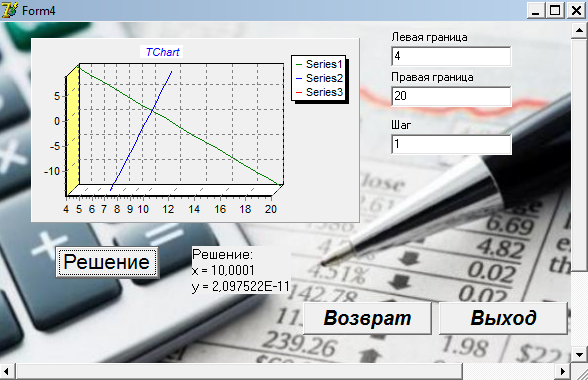



Unit4;

procedure TForm4.Button3Click(Sender: TObject);

begin

close();

end;

procedure TForm4.Button1Click(Sender: TObject);

begin

form1.visible:=true;

form4.visible:=false;

end;

function Fy(x:real): real;

begin

Fy := (60-6*x)/4;

end;

function Fx(x:real): real;

begin

Fx :=(100+2*x)/10;

end;

procedure TForm4.Button2Click(Sender: TObject);

var a, b ,h, x1, y, x2: Double;

begin

Chart1.Series[0].Clear;

Chart1.Series[1].Clear;

Chart1.Series[2].Clear;

a := StrToFloat(LabeledEdit1.Text); //левая граница

b := StrToFloat(LabeledEdit2.Text); //правая граница

h := StrToFloat(LabeledEdit3.Text); //шаг

x1 := a;

repeat

y := Fy(x1);

x2 := Fx(y);

hart1.Series[0].AddXY(x1,y,FloatToStrF(x1,ffGeneral,4,3),clRed); //график F(x)

hart1.Series[1].AddXY(x2,y,FloatToStrF(y,ffGeneral,4,3),clGreen); //график F(y)

x1 := x1 + h; //приращение координат

until x1 > b;

x1 := a;

repeat

y := Fy(x1);

x2 := Fx(y);

x1 := x1 + h/10000;

if ( x1 < x2 + h/10000 ) and ( x1 > x2 - h/10000 ) then

begin

Label5.Caption := 'Решение: ' +#13+ 'x = '+FloatToStrF(x1,ffGeneral,7,7)+#13;

Label5.Caption :=Label5.Caption + 'y = '+FloatToStrF(y,ffGeneral,7,7);

Chart1.Series[2].AddXY(x1,y,FloatToStrF(x1,ffGeneral,4,3),clBlue);

end;

until x1 > b;

end;end.

2.9 Лабораторная работа