Математическое моделирование - Никишев. Н. Ульянова В. К. Никишев Математическое моделирование
 Скачать 6.84 Mb. Скачать 6.84 Mb.
|
|
18. Смоделировать ту же ситуацию, что и в задании к варианту 17, при условии неограниченной области блуждания и ответить на заданный вопрос, 19.Смоделировать полет пчелы. На плоскости (поляне) случайным образом растут медоносные растения с заданной концентрацией (на 1 м3). В центре — улей, из которого вылетает пчела. Пчела может долететь от одного растения до любого другого растения, но вероятность выбора монотонно уменьшается с увеличением расстояния между растениями (по некоторому закону). Какова вероятность посещения пчелой конкретного заданного растения за заданное количество элементарных перелетов? 20. Реализовать модель плоского броуновского движения п частиц в прямоугольнике. Частицы считать шариками конечного размера. Удары частиц друг о друга и о стенки моделировать как абсолютно упругие. Определить п этой модели зависимость давления газа на стенки от числа частиц. 21. Разработать в деталях и реализовать модель перемешивания (диффузии) газов в замкнутом сосуде. В начальный момент времени каждый газ занимает половину сосуда. Изучить с помощью этой модели зависимость скорости диффузии от различных входных параметров, 22. Реализовать имитационную модель системы «хищник—жертва» по следующей схеме. «Остров» размером 20^20 заселен дикими кроликами, волками и волчицами, Имеется по несколько представителей каждого вида. Кролики в каждый момент перемещаются с одинаковой вероятностью 1/9 передвигаются в один из восьми соседних квадратов (за исключением участков, ограниченных береговой линией) или просто сидят неподвижно. Каждый кролик с вероятностью 0,2 превращается в двух кроликов. Каждая волчица передвигается случайным образом, пока в одном из соседних восьми квадратов не окажется кролик, за которым она охотится. Если волчица и кролик оказываются в одном квадрате, волчица съедает кролика и получает одно очко. В противном случае она теряет 0,1 очка. Волки и волчицы с нулевым количеством очков умирают. В начальный момент времени все волки и волчицы имеют 1 очко. Волк ведет себя подобно волчице до тех пор, пока в соседних квадратах не исчезнут все кролики; тогда, если волчица находится в одном из восьми близлежащих квадратов, волк гонится за пей.Если волк и волчица окажутся в одном квадрате и там пег кролика, которого можно съесть, они производят потомство случайного пола. Пронаблюдать за изменением популяции в течение некоторого периода времени. Проследить, как сказываются на эволюции популяций изменения параметров модели. 23.Промоделировать процесс распространения инфекции стригущего лишая по участку кожи размером n*n (п — нечетное) клеток. 3.5 Моделирование оптимальных систем 1 Cмоделировать маршрут движения катера Внутри водоема правильной круглой формы радиуса R расположен маленький островок радиуса r. Вычислите и укажите кратчайший прямой маршрут катера, соединяющий какие-нибудь точки берега и имеющий промежуточный причал у островка. 2 Место для завода Четыре населенных пункта расположены в вершинах выпуклого четырехугольника. В каком месте следует построить завод, чтобы сумма расстояний от него до всех четырех данных пунктов была наименьшей? .3 Газетный киоск Вдоль прямой улицы по одну сторону от нее стоят несколько домов. В каком месте улицы нужно установить газетный киоск, чтобы сумма расстояний от него до всех домов была наименьшей? 4 Где построить школу? В одном населенном пункте живет больше детей, чем в другом. В каком месте следует построить школу, чтобы общие затраты на перевозку детей были минимальны, если эти затраты пропорциональны как количеству детей, так и расстоянию от населенного пункта до школы? 5. С наименьшей суммой расстояний Три населенных пункта расположены в вершинах остроугольного треугольника. Где нужно построить завод, чтобы сумма расстояний от него до всех трех данных пунктов была иаименьшей? 6. Проселочная дорога Через город проходит магистраль, на некотором расстоянии от которой находится населенный пункт. 7. Направление магистрали В каком направлении через город должна проходить магистраль, чтобы сумма расстояний от нее до двух данных населенных пунктов была наименьшей? 8. Наилучшее расположение Как должна проходить магистраль, чтобы сумма расстоянии от нее до трех данных населенных пунктов была наименьшей? 9. Выбор маршрута Три завода расположены в вершинах разностороннего треугольника и соединены друг с другом магистралями. Внутри этого треугольника на одинаковом расстоянии от магистралей находится населенный пункт, который напрямую соединен дорогой с каждым заводом. Каким должен быть кратчайший замкнутый маршрут автобуса, предназначенного для развозки жителей населенного пункта по всем трем заводам? 10. Как проложить дорогу? Две магистрали пересекаются под углом, внутри которого расположен населенный пункт. Как проложить через этот пункт прямую дорогу, соединяющую магистрали, чтобы замкнутый маршрут автобуса, проходящий по этой дороге и участкам магистралей между точками их пересечения с дорогой и друг с другом, был кратчайший 11. Кратчайший замкнутый маршрут Три магистрали, пересекаясь, образуют остроугольный треугольник. Как проложить кратчайший маршрут автобуса, имеющий выезды к каждой из трех магистралей? 12. Строительство водопровода Для снабжения водой двух населенных пунктов, расположенных по одну сторону от канала, требуется на берегу канала построить водонапорную башню. В каком месте следует построить башню, чтобы суммарная длина труб от нее до каждого из пунктов (по прямой) была наименьшей? 13. Кратчайшая дорога Магистраль п канал пересекаются под углом меньше 45°, внутри которого расположен населенный пункт. Как проложить кратчайшую дорогу, проходящую от одного пункта сначала к берегу канала, а затем к магистрали? 14. Мост через какал Два населенных пункта расположены но разные стороны от широкого капала. Требуется построить мост через канал (перпендикулярно берегам) и проложить к нему дороги от обоих пунктов. В каком месте следует построить мост, чтобы в итоге путь между данными пунктами оказался кратчайшим? 15. Железнодорожная платформа По одну сторону от железной дороги расположены два населенных пункта. В каком месте дороги следует построить платформу заданной длины, чтобы сумма расстояний от нее до данных пунктов была наименьшей? 16. Кратчайший маршрут Две магистрали пересекаются под острым углом, внутри которого расположены два населенных пункта. Как проложить кратчайший маршрут автобуса, соединяющий два данных пункта и имеющий выезды к каждой из двух магистралей в заданном порядке? Задания для метода « Линейное программирование» 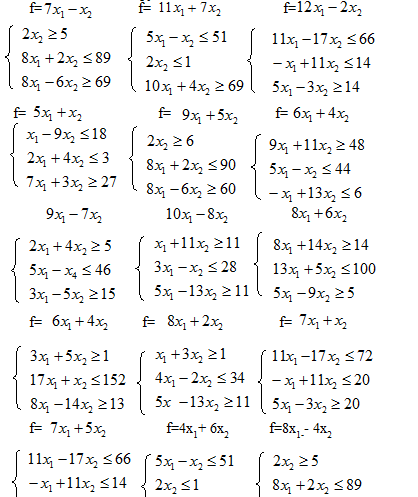 Индивидуальные задания - модель движения материальной точки Аристотеля и Ньютона; - модель Солнечной системы Птолемея, Коперника, Кеплера; - простейшую демографическую модель; - модель многоотраслевой экономики Леонтьева; - модель процесса распространения эпидемий; - модель динамики численности биологических популяций; - модель относительных движений в классической механике; - модель остывания нагретых тел в атмосфере; - математическую модель процесса загрязнения воды; - модель колебательных процессов в физике. - модель биологической системы «хищник-жертва»; - модель биологической системы конкурирующих популяций; - модель поведение динамики многочастичной системы; - модели марковских случайных процессов; - модель поведение динамической системы, описываемой уравнениями Колмогорова.; -модель управления различными летательными объектами; - модель исследования систем на основе матричных методов пространства состояния; - модели экспертных систем; - модели управления педагогическими системами; - модели геоинформационных систем . ЛИТЕРАТУРА 1. Алексеев, О. Г. Управление в системах РАВ / О. Г. Алексеев и др. - М. : МО, 1980. - 600 с. 2. Белошапка, В. Информатика как наука о буквах / В. Белошапка // Информатика и образование. - 1992. - № 1. -С 6-12. 3. Вершинин, О. Е. Компьютер для менеджера / О. Е. Вершинин. - М. : Высшая школа, 1990. - 240 с. 4. Глушков, В. М. Кибернетика / В. М. Глушков. - М. : Наука, 1986. 5. Глушков, В. М. Введение в АСУ / В. М. Глушков. -Киев. : Техника, 1974. 6. Глушков, В. М. Основы безбумажной информатики / В. М. Глушков. - М. : Наука, 1978. 7. Горстко, А. Б. Познакомтесь с математическим моделированием / А. Б. Горстко. - М. : Знание, 1991. 8. Гулд, Х. Компьютерное моделирование в физике /Х. Гулд и др. - М. : Мир, 1990. 9. Ершов, А. П. Об информационной модели машин / А. П. Ершов // Микропроцессоры, средства и системы. - 1985. - № 4. - С 2. 10. Заварыкин, В. М. Численные методы / В. М. Заварыкин. - М. : Просвещение, 1991. 11. Ивахненко, А. Т. Перцептрон - система распознавания образов / А. Т. Ивахненко и др. - Киев. : Наукова думка, 1975. 12. Кристофидес, Н. Теория графов. Алгоритмическая наука / Н. Кристофидес. - М. : Мир, 1978. 13. Кузин, Л. Т. Основы кибернетики / Л. Т. Кузин. - М. : Энергия, 1973. 14. Курицкий, Б. Я. Оптимизация вокруг нас / Б. Я. Курицкий. - Л. : Машиностроение, 1989. 15. Кушниренко, А. Г. Основы информатики и вычислительной техники / А. Г. Кушниренко. - М. : Просвещение, 1991. 16. Лященко, И. Н. Линейное и нелинейное программирование / И. Н. Ляшенко. - Киев. : Виша школа, 1975. 17. Мудров, А. Е. Численные методы для ПЭВМ на языках Бейсик,Фортран и Паскаль / А. Е. Мудров. - М. : МП “Раско”, 1992. 18. Никишев, В. К. Математический справочник-словарь по информатике и вычислительной технике / В. К. Никишев. - Чебоксары. : ЧГПИ, 1994. 19. Никишев, В. К. Использование IBM в учебном процессе / В. К. Никишев. - Чебоксары. : ЧГПИ, 1994. 20. Никишев, В. К. Основы программирования на ЦВМ и СЦВМ / В. К. Никишев. - Казань. : Министерство обороны, 1985. 21. Самарский, Н. Н. Компьютеры, модели, вычислительный эксперимент. Введение в информатику с помощью математического моделирования / Н. Н. Самарский. - М. : Наука, 1988. 22. Фомин, С. В. Математические проблемы в биологии. / С. В. Фомин. - М. : Наука, 1973. 23. Фридман, М. М. Наглядность и моделирование в обучении / М. М. Фридман. - М. : Знание, 1984. 24. Эберт, К. Компьютеры. Применение в химии / К. Эберт. - М. : Мир, 1988. Оглавление 1. Введение 2. Лабораторные работы по моделированию…………………4 2.1 Лабораторная работа №1 Тема: Методы исследования дифференциальных уравнений с использованием разных информационных технологий…… 8 2.2 Лабораторная работа № 2 Тема: Свободное падение тел………………………………… 8 2.3 Лабораторная работа № 3 Тема: Исследование динамики объектов, брошенных под углом к горизонту………………………………………….40 2.4 Лабораторная работа №4 Тема: Исследования динамики популяций хищника и жертвы………………………………….68 2.5 Лабораторная работа №5 Тема: Моделирование движения заряженных частиц и небесных тел……………………………81 2.6 Лабораторная работа № 6 Тема: Исследование динамики полета ракеты.……..………..98 2.7 Лабораторная работа № 6 Тема: Разработка информационной модели студента……..115 2.8 Лабораторная работа № 8 Тема: Исследование экономических систем ……..………….127 Тема: Исследование систем массового обслуживания … 143 2.9 Лабораторная работа № 9 Тема: Исследование оптимальных систем……………………150 2.10 Лабораторная работа №10 Тема. Моделирование объектов методом пространства состояния………………………………… 159 Литература Учебное издание Лабораторный практикум по моделированию Учебно-методическое пособие Подписано в печать_27.02.07 Формат 60х80/16. Бумага писчая. Печать оперативная. Усл. печ. л. 18.7 Тираж 50 экз. Заказ N . ГОУ ВПО «Чувашский государственный университет им. И. Н. Ульянова» Отпечатано на участке оперативной полиграфии ГОУ ВПО «Чувашский государственный университет им. И.Н. Ульянова» 428000, Чебоксары, |
