Курсовая работа. Практические+занятия+студенты+(1) (1) (1). Надежность

• Название: Надежность
• Анкор: Курсовая работа
• Дата: 19.10.2022
• Размер: 0.79 Mb.
• Имя файла: Практические+занятия+студенты+(1) (1) (1).docx
• Тип: Учебное пособие; #742930
• страница: 11 из 32

n

Для построения кривой накопленных опытных вероятностей (рис. 6.3) по оси абсцисс откладывают в масштабе значение показателя надёжности t, а по

оси ординат – накопленную опытную вероятность _ p_i.

i1

Σp_i
1,0
0,8

0,6
0,4
0,2
0

3,6 4,3 5,0 5,7 6,4 7,1 7,8 8,5

t,

тыс. км

Рис. 6.3. Кривая накопленных опытных вероятностей


n
Точки кривой накопленных опытных вероятностей образуются пересече- нием ординаты, равной сумме вероятностей _ p_i, и абсциссы конца данного

i1

интервала. Полученные точки соединяют с началом первого интервала.

Кривая накопленных опытных вероятностей более удобна для решения практических задач по сравнению с гистограммой и полигоном распределе- ния, так как в этом случае нет необходимости определять площади, а все ис- комые показатели находят по оси ординат. Например, для определения коли- чества изделий, требующих ремонта при наработке до 6,6 тыс. ч необходимо на оси абсцисс найти точку 6,6 и по оси ординат определить накопленную опытную вероятность: Σp_i= 0,64.

Физическое количество N_изд= 0,64∙79 = 51 изделие.

С помощью этой же кривой можно найти количество отказавших изделий в любом интервале наработки. Например, в интервале наработки 5,5…6,6 тыс. ч N_изд= (0,64 - 0,24)∙79 = 32 изделия.

6. 
   Определениекоэффициентавариации
   

Коэффициент вариации
v^,

t C
где С – смещение рассеивания показателя надёжности – расстояние от начала координат до начала рассеивания случайной величины.

Смещение рассеивания рассчитывают по формулам:

- при отсутствии статистического ряда (N< 25):

С t<sub>1

</sub> t₃  t_{1 ,}

2

где t₁ и t₃ – значения первой и третьей точек информации в порядке их воз- растания;

- при наличии статистического ряда (N> 25):
C t_н1  0,5A,
где t_н1 – начало первого интервала статистического ряда;

А – длина интервала. Тогда

С 3600  0,5  700  3250 ч.
Коэффициент вариации

v 972 6214 3250 0,33.

7. 
   Выбор теоретического закона распределениядлявыравниванияопытной информации
   

Испытания техники на надёжность связаны с организационными трудно- стями и большими материальными затратами, что ограничивает как количе- ство испытываемых машин, так и длительность их испытаний. Кроме того, ре- зультаты испытаний зависят от квалификации водителей и наблюдателей, кли- матических условий, сортов и чистоты топливосмазочных материалов, каче- ства запасных частей и т.д. Перечисленные факторы не позволяют переносить результаты испытаний на надёжность на машины той же марки, не входящие в выборочную совокупность без соответствующих корректив, которые заклю- чаются в том, что на основании первичной информации о выборочной сово- купности машин определяют теоретический закон распределения показателя надёжности для генеральной совокупности машин. Этот закон выражает об- щий характер изменения показателя надёжности и исключает частные откло- нения, связанные с недостатками первичной информации. Такой процесс за- мены опытного распределения теоретическим называют процессом выравни- вания или сглаживания статистической информации.

Для выравнивания распределений показателей надёжности техники и её элементов наиболее широко используют закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ).

1. 
   Использованиедлявыравниванияраспределенияопытнойинформациизакона нормальногораспределения
   

ЗНР характеризуется дифференциальной и интегральной функциями. От- личительная особенность дифференциальной функции – симметричное рассе- ивание частных значений показателей надёжности относительно среднего зна- чения.

Дифференциальную функцию описывают уравнением:

f(t_i) 

t_it<sup>2


1 </sup> 2 ²

e ,

где σ– среднее квадратическое отклонение;

t– показатель надёжности;

^t– среднее значение показателя надёжности.

Если принять ^t=0 и σ= 1, то получим выражение для центрированной нормированной дифференциальной функции:

где

_z t_i t_.

i _
z  ¹ 2

• 
  _z2
  

_ie
2 _,

Центрированная нормированная функция дана в приложении.

Для определения дифференциальной функции через центрированную нормированную функцию используют уравнение:

_{ft } A z_i

i _
При этом,  (z)   (z).

В качестве примера определим значение дифференциальной функции в первом интервале статистического ряда.
f 3600 ...4300   ⁷⁰⁰ ^{ 3950  6214 }  0,72 2,33  0,72  0,03  0,02.



972 _



972 _

Интегральная функция распределения:

Q(t_i) 

1 _{ e}


t




t_it ²

2 ²
dt.

Интегральная нормированная функция примет вид:

_{ } z ₁

z_ z²

Q₀ z_i

 _(z)  _ e

² dz.

 ^2 
Если z< 0, то Q₀ (z)  1 Q₀ (z) .

Обратный переход от нормированной функции к исходной делается по формуле:
Qt_i  Q₀ z_i.
Определим значение интегральной функции в первом интервале стати- стического ряда:




Q3600 ...4300   Q^{ 4300  6214 }  Q1,97  1  Q1,97  1  0,98  0,02 .




0 ^ ₉₇₂ ^ 0 0
Рассчитанные аналогичным образом значения дифференциальной и инте- гральной функций по всем интервалам статистического ряда сведём в таблицу 6.4.

Таблица 6.4 – Значения дифференциальной и интегральной функций при ЗНР

Интер- вал, тыс. ч	3,6…4,3	4,3…5,0	5,0…5,7	5,7…6,4	6,4…7,1	7,1…7,8	7,8…8,5
f(t)	0,02	0,08	0,19	0,28	0,24	0,13	0,04
Q(t)	0,02	0,11	0,3	0,58	0,82	0,95	0,99

На основании полученных значений f(t) и Q(t) могут быть построены гра- фики дифференциальной (рис. 6.4) и интегральной функций (рис. 6.5). Диффе- ренциальная функция заменяет полигон распределения, а интегральная – кри- вую накопленных опытных вероятностей.

По оси абсцисс дифференциальной и интегральной кривых откладывают в определённом масштабе значения интервалов статистического ряда, а по оси ординат – значения f(t) или Q(t). Точки на графике дифференциальной функ- ции находят на пересечении абсцисс, равных серединам интервалов статисти- ческого ряда, и ординат, равных f(t), а на графике интегральной функции – на пересечении абсцисс, равных концам интервалов статистического ряда, и ор- динат, равных Q(t).

Для определения количества изделий, отказавших в каком-то интервале наработки, необходимо площадь под дифференциальной кривой, соответству- ющую этому интервалу, отнести к общей площади под дифференциальной кривой и полученное значение перемножить на общее количество испытыва- емых изделий.

f (t)

0,3
0,25
0,2
0,15
0,1

0,05
0

3,6 4,3 5,0 5,7 6,4 7,1 7,8 8,5
Рис. 6.4. График дифференциальной функции

t,

тыс. км

Q(t)

1,0
0,8
0,6
0,4

0,2
0

3,6 4,3 5,0 5,7 6,4 7,1 7,8 8,5
Рис. 6.5. График интегральной функции

t,

тыс. км

Количество изделий, отказавших в каком-либо интервале наработки, на графике интегральной функции определяют перемножением полученного зна- чения по оси ординат на общее количество изделий.

С помощью приведённых выше уравнений можно определить количество отказавших изделий не только в интервалах статистического ряда, но и в лю- бом интервале наработки. Эту задачу можно решать по дифференциальной или интегральной функции. Например, необходимо определить количество из- делий, отказавших в интервале наработки 5700…6350 ч:

- по дифференциальной функции:

f 5700 ...6350   ⁶⁵⁰ ^{ 6025  6214 }  0,670,19  0,67  0,39  0,26 , или



972 _



972 _

0,26  79  21 изделие.

- по интегральной функции:

Q5700 ...6350   Q0...6350  Q0...5700   Q^{ 6350  6214 }  Q^{ 5700  6214 } 

^{0 } 972

 ₀

 





972 _

 Q₀ 0,14 Q₀  0,53  Q₀ 0,14 1  Q₀ 0,53  0,56  1  0,70  0,26,

или

0,26  79  21 изделие.

2. 
   ИспользованиедлявыравниванияраспределенияопытнойинформациизаконараспределенияВейбулла
   

Дифференциальную функцию, или функцию плотности вероятностей определяют при законе распределения Вейбулла по уравнению:

_𝑡𝑏−1

−(^𝑡)𝑏

𝑓⁽𝑡⁾ = 𝑏

_𝑎𝑏 𝑒

𝑎 _,

где аи b– параметры распределения Вейбулла.

Параметр b определяется по таблице приложения. Для этого необходимо предварительно найти коэффициент вариации. Из таблицы выписывают зна- чение параметра b, коэффициенты K_Ви С_В. При v = 0,33 b = 3,3; K_В= 0,90 и С_В= 0,30.

Параметр арассчитывают по одному из уравнений: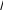

a t C K_B

или
a 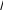
C_B.

В нашем случае,

a 6214 3250 0,90  3293 ч.

Дифференциальную функцию определяют по приложению. При этом ис- пользуют уравнение:
ft  ^Af^{ tci C} ,




 

a _ a _
где А– длина интервала статистического ряда;

t_ci– середина интервала статистического ряда;

С– смещение.

Находят дифференциальную функцию в первом интервале статистиче- ского ряда:

f3600 ...4300  

⁷⁰⁰ f^{ 3950  3250 }  0,21 f0,21  0,21 0,13  0,02.



3293 _



3293 _

Интегральная функция:

 ^t<sup>b

</sup> 

Qt  1  e^{ a} .
Эту функцию также определяют по приложению. При этом используют уравнение:
Qt  Q^{ tкi C}




 ^,

 ^a 
где t_кi– значение конца i-го интервала.

Например, интегральная функция в первом интервале статистического ряда:

Q3600 ...4300   Q^{ 4300  3250 }  Q0,32  0,03.




 

_ 3293 _
Аналогично определим значения дифференциальной и интегральной функций в остальных интервалах статистического ряда (табл. 6.5).

Таблица 6.5 – Значения дифференциальной и интегральной функций при ЗРВ

Интер- вал, тыс. ч	3,6…4,3	4,3…5,0	5,0…5,7	5,7…6,4	6,4…7,1	7,1…7,8	7,8…8,5
f(t)	0,02	0,11	0,20	0,24	0,21	0,13	0,05
Q(t)	0,03	0,13	0,33	0,58	0,81	0,95	0,99

С помощью ранее приведённых уравнений закона распределения Вей- булла можно найти количество отказавших изделий не только в каждом ин- тервале статистического ряда, но и в любом интервале наработки.

Например, определим количество отказавших изделий в интервале нара- ботки 5700…6350 ч, если предположить, что рассеивание ресурса изделий подчиняется закону распределения Вейбулла. Задача может быть решена как по дифференциальной, так и по интегральной функции.

При решении по дифференциальной функции:

f5700 ...6350  

⁶⁵⁰ f^{ 6025  3250 }  0,20 f0,84  0,20 1,16  0,23,


или



3293 _



3293 _

0,23  79  18 изделий.
При решении по интегральной функции:

Q5700 ...6350   Q0...6350  Q0...5700   Q^{ 6350  3250 }  Q^{ 5700  3250 } 



_ 3293

  

_{ } 3293 _

 Q0,94 Q0,74  0,56  0,31  0,25,

или

0,25  79  20 изделий.

8. 
   Оценка совпадения опытного и теоретического законов распределения по-казателей надёжности покритериюсогласия
   

В процессе оценки совпадения определяют степень совпадения или рас- хождения опытной вероятности и дифференциальной функции, или же накоп- ленной опытной вероятности и интегральной функции в интервалах статисти- ческого ряда. Для определения совпадения или расхождения выбирают раз- личные критерии: сумму квадратов отклонения дифференциальной функции от опытной вероятности, наибольшее или суммарное отклонение кривой накопленных опытных вероятностей от интегральной кривой теоретического закона распределения и т.д.

Однако, как бы не велико было совпадение, оно свидетельствует только о том, что выбранный закон не противоречит опытному распределению, но не гарантирует того, что этот закон в данном случае лучше, чем какой-либо дру- гой, выравнивает опытную информацию. Наиболее удачно критерий согласия используют при выборе одного теоретического закона из нескольких. В этом случае наиболее приемлемым окажется тот закон распределения, совпадение которого с опытным распределением характеризуется наименьшим значением расхождения.

При обработке информации по показателям надёжности техники наибо- лее часто применяют критерий согласия Пирсона χ², определяемый по уравне- нию:

n_y

 ²  _

m m²


i тi
,

m

^i1 тi
где n_y– количество интервалов укрупнённого статистического ряда;

m_i– опытная частота в i-м интервале статистического ряда;

m_тi– теоретическая частота в i-м интервале. Теоретическая частота:
m_тi NQt_i Qt_i1 ,
где N– количество точек информации;

Q(t_i) и Q(t_i-1) – интегральные функции i-го и (i-1)-го интервалов статисти- ческого ряда.

Для определения χ² строят укрупнённый статистический ряд, соблюдая условие: n_у> 4, m_i≥ 5 (табл. 6.6). При этом допускается объединение соседних интервалов, в которых m_i< 5. Проанализируем статистический ряд информа- ции о ресурсах изделия. Можно заметить, что m₁ = 4 и m₂ = 1,5 меньше пяти, поэтому первый и второй интервалы статистического ряда объединяют. Опыт- ная частота в объединённом интервале будет равна сумме частот объединяе- мых интервалов. В остальных интервалах статистического ряда опытные ча- стоты больше пяти, поэтому эти интервалы оставляем без изменения.

Таблица 6.6 – Укрупнённый статистический ряд

Интервал, тыс. ч	3,6…5,0	5,0…5,7	5,7…6,4	6,4…7,1	7,1…7,8	7,8…8,5
mi	7	16	22	22	6,5	5,5
При законе нормального распределения
Q(t)	0,11	0,3	0,58	0,82	0,95	0,99
miт	8,7	15	22,1	19	10,3	3,2
При законе распределения Вейбулла
Q(t)	0,13	0,33	0,58	0,81	0,95	0,99
miт	10,3	15,8	19,8	18,2	11,1	3,2

Теоретические частоты, например, в первом и втором интервалах при ЗНР определяют следующим образом:

m_1т  790,11  0  8,7;

m_2т  790,3  0,11  15,1.
Для данного примера критерий согласия Пирсона:







- при законе нормального распределения:

 ² 

7  8,7² 8,7

16 15²



15

22  22,1² 22,1

22 19²



19

6,5 10,3² 10,3

5,5  3,2² 3,2
 3,5;




- при законе распределения Вейбулла:

 ² 

7 10,3² 10,3

16 15,8²



15,8

22 19,8² 19,8

22 18,2²



18,2

6,5 11,1²



11,1

5,5  3,2² 3,2
 5,65.

Для дальнейших расчётов выбирают тот закон распределения, у которого меньше критерий Пирсона χ². Судя по значениям критериев согласия ЗНР и ЗРВ, приходим к выводу, что применительно к ресурсам изделия более прием- лемым считают закон нормального распределения.

9. 
   Определение доверительных границ рассеивания одиночного и среднегозначенийпоказателянадёжности
   

1. 
   Определение доверительных границ рассеивания при законе нор-мальногораспределения
   

Для определения доверительных границ рассеивания одиночного значе- ния показателя надежности при законе нормального распределения вначале находят абсолютную ошибку е_β:

e_  t_ ,
где t_β– коэффициент Стьюдента.

Нижняя доверительная граница:
^{tн t t} ,

 
где t– среднее значение показателя надежности.

Верхняя доверительная граница:
^{tв t t} .

 

Доверительный интервал:




^{I  tв tн}.
Для примера по обработке информации по ресурсу изделия коэффициент Стьюдента при β= 0,90 равен: t_β= 1,66,

нижняя доверительная граница:

др

t
^{н 6214 1,66  972  4600} ч;
верхняя доверительная граница

др

t
^{н 6214  1,66  972  7828} ч;
доверительный интервал
I_  7828  4600  3228 ч.
Расчетная схема и физический смысл доверительных границ среднего значения показателя надежности те же, что и для одиночного показателя. Раз- ница заключается в значении среднего квадратического отклонения.

Среднее квадратическое отклонение рассеивания среднего значения по- казателя надежности:

t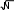
 ^ ,
где N– количество точек информации, по которому определено среднее зна- чение показателя надежности.

Нижняя доверительная граница среднего значения показателя надежно-

сти: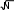


t^н t t_

 _.

Верхняя доверительная граница среднего значения показателя надежно-

сти:


t^в t t_

 _.

Доверительный интервал среднего значения показателя надежности:
^I ^{ tв tн.}

 
Для приведённого примера по обработке информации по ресурсу изделия коэффициент Стьюдента t_β= 1,66,

нижняя доверительная граница:

др

t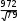
^н 6214 1,66  6034 ч;

верхняя доверительная граница:

др

t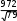
^в 6214 1,66  6394 ч;
доверительный интервал:
^{I  6394  6034  360} ч.

2. 
   Определение доверительных границ рассеивания при законераспределенияВейбулла
   

Доверительные границы рассеивания одиночного показателя надёжности при ЗРВ определяют по уравнениям:
t^н H^B ^{1   }a C;




_{ к} 

 ² 

t^в H^B ^{1   }a C,




_{ к} 

 ² 

H

к
где ^В– квантиль закона распределения Вейбулла;

а– параметр закона Вейбулла;

С – смещение начала рассеивания. Доверительный интервал:




^{I  tв tн}.
Для рассматриваемого примера при доверительной вероятности β = 0,90

_{tн  НВ}^{1  0,90} 


 3250  0,424  3293  3250  4646 ч;

др к^



³²⁹³

2 _

_{tв  НВ}^{1  0,90} 

 3250  1,4  3293  3250  7860 ч;

др к^



³²⁹³

2 _

I_  7860  4646  3214 ч.

Доверительные границы рассеивания среднего значения показателя надёжности при ЗРВ определяют по уравнениям: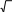

t^н t C^br C;

 3

t^в t C^br

• 
  C,
  

 1
где r₁ и r₃ – коэффициенты распределения Вейбулла, зависящие от доверитель- ной вероятности βи повторности информации N;

b – параметр закона распределения Вейбулла. Доверительный интервал:
^I ^{ tв tн.}

 
Для данного примера r₁ = 1,21; r₃ = 0,84; b = 3,3.

др

t
^н 6214  3250 ^3,3 0,84  3250  6062 ч;


др

t
^в 6214  3250 ^3,3 1,21  3250  6390 ч;

^{I  6390  6062  328} ч.

10. 
    Определение абсолютной и относительной предельных ошибок переносахарактеристикпоказателянадёжности
    

Наибольшая абсолютная ошибка переноса опытных характеристик пока- зателя надёжности при заданной доверительной вероятности равна значению е_βв обе стороны от среднего значения показателя надёжности.

Относительная предельная ошибка, %:

t^в t

_ ^100% 

t C

6394  6214

6214  3250

100%  6% (при ЗНР).