Материал по ТПР. Наличие хорошего по в соответствующей организации или фирме и хороших аппаратных средств это лишь необходимое, но не достаточное условие

• Название: Наличие хорошего по в соответствующей организации или фирме и хороших аппаратных средств это лишь необходимое, но не достаточное условие
• Дата: 07.10.2020
• Размер: 0.64 Mb.
• Имя файла: Материал по ТПР.doc
• Тип: Документы; #141401
• страница: 2 из 6

Тема 3. Процесс принятия решений и его этапы.

1.Процесс принятия решений (ППР).

ППР представляет собой многоэтапный процесс. Очень часто это достаточно длинный и мучительный процесс. Разные авторы по-разному подходят к вопросу об этапах ППР. Так, Г. Саймон выделяет в нем 3 этапа:

1. 
   поиск информации;
   
2. 
   поиск и нахождение альтернатив;
   
3. 
   выбор наилучшей альтернативы.
   

На первом этапе собирается вся доступная на момент ПР информация: фактические данные, мнения экспертов. Там где возможно строятся математические модели, проводятся социологические опросы, определяются взгляды на проблему со стороны активных групп, влияющих на ее решение.

Второй этап связан с определением того, что можно, а чего нельзя делать в имеющейся ситуации, т.е. с определением вариантов решений (альтернатив).

Третий этап включает в себя сравнение альтернатив и выбор наилучшего варианта (или вариантов) решения.

Ряд авторов определяют следующие этапы ППР:

- Определение альтернативных способов действия. Должен быть задан подходящий набор целей и указаны соответствующие им меры эффективности; это дает возможность определить степень, с которой заданные цели могут быть достигнуты с помощью раз­личных способов действия. Для каждого способа действия воз­можные исходы описываются в единицах принятых мер эффективности. Кроме того, необходимо указать, как научаемый процесс (задача) развивается во времени, и описать способ сбора информа­ции.

- Описание вероятностей возможных исходов. При этом требуется, чтобы неопределенность, связанная с альтернативными решениями, была выражена численно через распределение ве­роятностей (если это возможно). В результате такой операции становится известной вероятность каждого возможного исхода для каждого принятого решения.

- Ранжировка предпочтений возможных исходов через их полезность. Для этого выбирают меру эффективности, а затем с ее помощью представляют в числовой форме как отношение лица, принимающего решение, к последствиям (исходам), так и вероят­ности возможных исходов.

- Рациональный синтез информации, полученной ни первых трех этапах. Следует проанализировать и эффективно исполь­зовать всю полученную информацию, для того чтобы решить, ка­кой из возможных альтернатив следует отдать предпочтение. Данный этап включает также анализ чувствительности.

Эти этапы являются основой подхода к принятию решений с точки зрения здравого смысла. Отличительной чертой процесса принятия решений является степень формализации каждого этапа.
2.Множество Эджворта – Парето.
Допустим, имеются две альтернативы: А и В. Назовем альтернативу А доминирующей по отношению к альтернативе В, если по всем критериям оценки альтернатива А не хуже, чем альтернатива В, а хотя бы по одному критерию оценка А лучше.

При этом альтернатива В называется доминируемой.

Пример. При покупке телевизора с учетом 2-х критериев: стоимость и функциональность имеются 3 варианта телевизоров (альтернативы), которые представлены в следующей таблице:

Альтернатива	Критерий
	Стоимость	Функциональность
1. Телевизор 1	небольшая	малая
2. Телевизор 2	высокая	высокая
3. Телевизор 3	небольшая	высокая

Изобразим альтернативы графически
Функциональность

2 3

Высокая
1

Малая

Стоимость

Высокая Небольшая
Из рисунка видно, что альтернатива 3 лучше альтернатив 1 и 2, потому что она не хуже по критериальным оценкам каждой из двух альтернатив, а по одному из критериев явно лучше.

Предположим, что телевизоры 3-го вида закончились. Тогда телевизоры 1 и 2 вида не находятся в отношении доминирования. По одному из критериев лучше альтернатива 2, по другому – альтернатива 1.

Пусть задана группа альтернатив. Сравним все альтернативы попарно и исключим те из них, которые доминируются хотя бы одной из оставшихся альтернатив. Тогда оставшиеся (недоминируемые) альтернативы принадлежат множеству Эджворта – Парето (Э-П).

Альтернативы, принадлежащие множеству Э-П невозможно сравнить непосредственно на основе критериальных оценок, т.е. про две альтернативы из этого множества нельзя сказать, которая лучше, а которая хуже. Но если решение должно быть принято, то сравнение альтернатив, принадлежащих множеству Э-П, возможно на основе дополнительной информации. Так, в нашем примере покупатель должен решить, что для него важнее: экономия денег или обилие многофункциональности телевизора.

Нетрудно убедиться, что множество Э-П включает в себя наиболее «контрастные» альтернативы, сложные для сравнения. Если стоит задача выбора одной лучшей альтернативы, то она обязательно принадлежит множеству Э-П. Поэтому во многих методах ПР очень важен этап выделения множества Э-П из всего множества заданных альтернатив.

Один из возможных способов решения этой задачи состоит в попарных сравнениях альтернатив и исключении доминируемых.

Задача выделения множества Э-П обычно рассматривается как предварительная. За ней следует наиболее существенный этап принятия решений.
3. Типовые задачи принятия решений.
Задачи ПР отличаются большим многообразием, классифицировать их можно по различным признакам, характеризующим количество и качество доступной информации для ПР. В общем случае ЗПР можно представить следующим набором информации:

,

где T- постановка задачи (например, выбрать лучшую альтернативу или упорядочить весь набор);

A- множество допустимых альтернатив;

K- множество критериев;

X- множество методов измерения предпочтений (например, использование различных шкал);

F-отображение множества допустимых альтернатив в множество критериальных оценок (исходы);

G- система предпочтений эксперта;

D- решающее правило, отражающее систему предпочтений.
Любой из элементов этого набора может служить классификационным признаком ПР. Рассмотрим традиционные классификации:

1. По виду отображения F. Отображение множества A в K может иметь детерминированный характер, вероятностный или неопределенный вид, в соответствии с которым ЗПР можно разделить на задачи в условиях определенности, на задачи в условиях риска и на задачи в условиях неопределенности.

2. Мощность множества K. Множество критериев выбора может содержать один элемент или несколько. В соответствии с этим ЗПР можно разделить на задачи со скалярным критериев и задачи с векторным критерием ( многокритериальные задачи ПР).

3. Тип системы G. Предпочтения могут формироваться одним лицом или коллективом, в зависимости от этого ЗПР можно классифицировать на задачи индивидуального ПР и задачи коллективного ПР.

Задачи принятия решений в условиях определенности. К этому классу относятся задачи, для решения которых имеется достаточная и достоверная количественная информация. В этом случае с успехом применяются методы математического программирования, суть которых состоит в нахождении оптимальных решений на базе математической модели реального объекта. Основные условия применимости методов математического программирования следующие:

1. 
   Задача должна быть хорошо формализована, т. е. имеется адекватная математическая модель реального объекта.
   
2. 
   Существует некоторая единственная целевая функция (критерий оптимизации), позволяющая судить о качестве рассматриваемых альтернативных вариантов.
   
3. 
   Имеется возможность количественной оценки значений целевой функции.
   
4. 
   Задача имеет определенные степени свободы (ресурсы оптимизации), т. е. некоторые параметры функционирования системы, которые можно произвольно изменять в некоторых пределах в целях улучшения значений целевой функции.
   

Задачи принятия решений в условиях риска. В тех условиях, когда возможные исходы можно описать с помощью некоторого вероятностного распределения, получаем ЗПР в условиях риска. Для построения распределения вероятностей необходимо либо иметь в распоряжении статистические данные, либо привлекать знания экспертов. Для решения задач этого типа применяются методы теории одномерной или многомерной полезности.

Задачи принятия решений в условиях неопределенности. Эти задачи имеют место тогда, когда информация необходимая для принятия решений является неточной, неполной, неколичественной, а формальные модели исследуемой системы либо слишком сложны, либо отсутствуют. В таких случаях привлекаются знания экспертов.

Следует отметить, что одним из условий существования ЗПР является наличие нескольких допустимых альтернатив, из которых следует выбрать в некотором смысле лучшую. При наличии лишь одной альтернативы, удовлетворяющей фиксированным условиям или ограничениям, ЗПР не имеет места.

ЗПР называется тривиальной, если она характеризуется исключительно одним критерием K и всем альтернативам присвоены конкретные числовые оценки в соответствии со значениями указанного критерия.

ЗПР перестает быть тривиальной даже при одном критерии, если каждой альтернативе соответствует не точная оценка, а интервал возможных оценок или распределение критериальных оценок альтернатив.

Нетривиальной считается задача при наличии нескольких критериев ПР.

Из всех вышеопределенных основных этапов ППР наибольшее внимание уделяется последнему этапу. Способы прохождения этапов ППР зависят не только от содержания задачи ПР, но и от опыта, привычек, личного стиля ЛПР и его окружения. Хотя эти же факторы присутствуют при сравнении альтернатив, здесь их роль заметно меньше.

Научный анализ проблем ПР начинается с момента, когда хотя бы часть альтернатив и (или) критериев известна.

Центральное место среди задач ПР занимают многокритериальные задачи выбора. Очевидно, что учет многих критериев приближает постановку задачи к реальной жизни. Обычно различают три основные ЗПР:

1. 
   Упорядочение альтернатив.
   

Для ряда задач вполне естественно требование определения порядка на множестве альтернатив, т.е. определение относительной ценности каждой из альтернатив.

2. 
   Распределение альтернатив по классам решений.
   

При большом числе альтернатив для облегчения выбора наилучшей альтернативы обычно их распределяют по классам. Например, различают группы товаров по качеству, группы книг по направлениям, группы (классы) автомобилей и т.д.

3. 
   Выделение лучшей альтернативы.
   

Эта задача традиционно считается одной из основных в ПР. Она часто встречается на практике. Выбор товара при покупке, выбор вуза при поступлении, выбор места работы, выбор проекта дома и т.д.

Кроме того, такие задачи распространены в мире политических решений, где альтернатив сравнительно немного, но они достаточно сложны для изучения и сравнения.
4. Многодисциплинарный характер науки о принятии решений.
Термин «принятие решений» встречается в различных научных дисциплинах.

Прежде всего, это экономика, где исследуются проблемы разумного, рационального использования ограниченных ресурсов потребителем и производителем.

Этот термин активно используется в когнитивной психологии. Психологи давно изучают особенности человеческой системы переработки информации.

Рассматриваются гипотезы о том, как влияет организация человеческой памяти на ППР. Психологи стремятся определить границы человеческих возможностей в задачах выбора.

В науке – политологии одним из главных объектов изучения является механизм принятия лидерами политических решений.

«Принятие решений» - один из основополагающих терминов в научном направлении, известном под названием «исследование операций». С помощью методов исследования операций разрабатываются модели, описывающие объективную реальность, определяется единственный критерий оптимальности решения, рассчитывается оптимальное решение. Существенное отличие проблем принятия решения от проблем исследования операций состоит в наличии многих критериев оценки качества решения. Компромисс между критериями может быть найден только на основе предпочтений ЛПР. Существует особый класс задач ПР, в которых модели имеют объективный характер, но качество решений оценивается по многим критериям. Эти задачи могут быть названы многокритериальными задачами с объективными моделями. Они находятся на границе между исследованием операций и принятием решений.

Принятие решений является одним из направлений прикладной математики. Ставятся и решаются задачи обоснования свойств функции полезности в зависимости от тех или иных условий, накладываемых на правила выбора.

Слова «принятие решений» можно встретить и в зоологии, когда исследуются проблемы естественного отбора среди представителей животного мира и растений.

Термин «принятие решений» является центральным для искусственного интеллекта. В рамках этого направления создаются различные компьютерные системы, имитирующие поведение людей при решении тех или иных проблем.

В информатике и вычислительной технике в последнее время уделяется большое внимание построению систем поддержки ПР, помогающих человеку в задачах выбора.

Рассмотрение процессов и проблем ПР в различных научных дисциплинах вполне оправдано. Центральным для этих проблем является сам акт выбора человеком одного из вариантов решений.

Основным предметом в науке о принятии решений является исследование процесса выбора. Она изучает, как человек принимает решения и как следует ему в этом помогать, создавая специальные методы и компьютерные системы.

Итак, принятие решений – это прикладная научная дисциплина. Создание методов принятия решений требует рассмотрения математических, психологических и компьютерных проблем

В связи с этим, в развитии ПР как научного направления принимают участие математики, психологи, политологи, специалисты по искусственному интеллекту, теории организаций, информатике, вычислительной технике.
Тема 4. Аксиоматические теории рационального поведения.
1.Рациональный выбор в экономике.
Задача выбора является одной из центральных в экономике. Два основных действующих лица в экономике – покупатель и производитель – постоянно вовлечены в процесс выбора.

Потребитель решает, что покупать и за какую цену. Производитель решает, во что вкладывать капитал, какие товары следует производить и др.

Основное допущение экономической теории состоит в том, что человек делает рациональный выбор. Рациональный выбор означает предположение, что решение человека является результатом упорядоченного процесса мышления. Для определения этого понятия в строго математической форме выводятся аксиомы рационального поведения.

При условии, что аксиомы справедливы, доказывается, что существует некая функция, устанавливающая человеческий выбор – функция полезности.

Под полезностью будем понимать величину, которая в процессе выбора максимизирует личность с рациональным экономическим мышлением. Иначе говоря – полезность – это воображаемая мера психологической и потребительской ценности различных благ.

С содержательной точки зрения делается предположение, что человек оценивает различные альтернативы и выбирает из них ту, полезность которой больше.

ЗПР с рассмотрением полезностей были первыми, которые привлекли внимание исследователей. Постановка таких задач заключается в следующем: человек выбирает какие-то действия, где на получаемый результат (исход) действия влияют случайные события, неподвластные человеку, но, имея некоторые знания о вероятностях этих событий, человек может рассчитывать наиболее выгодную совокупность и очерёдность своих действий. Человек, который следует аксиомам рационального выбора, называется в экономике рациональным человеком.

2. 
   Аксиомы рационального поведения.
   

Через x, у, z различные исходы (результаты) процесса выбора, а через

p, q – вероятности тех или иных исходов.

Лотереей называется игра с двумя исходами: исходом x, получаемым с вероятностью p, и исходом y, получаемым с вероятностью (1-p) ( рис.1)

p X



Рис.1. Лотерея с двумя исходами.
1-p Y
Ожидаемая (или средняя цена) лотереи определяется по формуле

px+(1-p)y.

Приведем аксиомы рационального выбора:

Аксиома 1. Пусть Pозначает строгое предпочтение (похожие на  в математике); R – не строгое предпочтение (похожее на ); I– безразличие (похожее на =). Аксиома 1. требует выполнения 2-х условий:

1. 
   связности: либо xRy, либо yRx, либо и то и другое вместе;
   

2) транзитивности: из xRy и yRx следует xRz

Аксиома 2. Если xIy, то (x, p, z) I (y, p, z) (через (x, p, y) обозначается лотерея на рис.1).

Аксиома 3. Если xPy, то xP (x, p, y) Py

Аксиома 4. Если xPyPz , то существует вероятность p, такая, что

yI (x, p, z).

Аксиомы, приведенные выше достаточно просты для понимания.

В предположении, что они выполняются, имеет место теорема, которая гласит, что существует числовая функция полезности

U, определенная на множестве исходов и такая, что:

1. 
   xRy тогда и только тогда, когда U (x) U(y)
   
2. 
   U (x, p, y) = p U(x) + (1-p) U(y)
   

3. Деревья решений
Для представления своих возможных действий и для нахождения последовательности правильных решений используется дерево решений.

Рассмотрим пример задачи с вазами. Экспериментатор случайно выбирает вазу из множества ваз, содержащего 700 ваз 1-го типа и 300 ваз 2-го типа. Если перед испытуемым находится ваза 1-го типа и он угадает это, то он получит выигрыш 350 у.е., если не угадает, то его проигрыш составит 50 у.е. Если перед ним ваза 2-го типа и он это угадает, то получит выигрыш 500 у.е., если не угадает, его проигрыш составит 100 у.е. Испытуемый может предпринять одно из следующих действий: d₁ – сказать, что ваза 1-го типа; d₂ – сказать, что ваза 2-го типа.

Условия задачи можно представить в таблице 1.

Таблица 1.

Тип вазы	Вероятность выбора вазы данного типа	Действия и выигрыш
		d1	d2.
1	0.7	350	-100
2	0.3	-50	500

Какое действие предпринять человеку?

На основе теории полезности для этого необходимо оценить среднюю (ожидаемую) полезность каждого из действий и выбрать действие с максимальной ожидаемой полезностью. Оценка полезности дает:

U (d₁) = 0.7 *350 – 0.3 * 50 = 230 y.e.

U (d₂) = 0.3 *500 – 0.7 * 100 = 80 y.e.

Следовательно, разумный человек выберет действие d_1, а не действие d_2.

Отсюда следует общий рецепт действий для рационального человека: для каждого действия определить ожидаемую полезность и выбрать действие с наибольшей полезностью.

Таблица 1. может быть представлена в виде дерева решений .

Дерево решений удобно использовать для представления своих возможных действий и для нахождения последовательности правильных решений, ведущих к максимальной ожидаемой полезности.
4. Парадокс Алле

Рассмотрим две лотереи, представленные на рис. 2.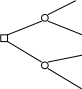


1 млн. 0,1 5 млн.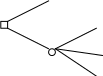

А С

0,1 5 млн. 0,9 0

В 0,89 0,11 1 млн.

1 млн. D

0,01 0,89

0 0
Рис. 2. Парадокс Алле
Обозначим: U ( 5млн )=1; U(1млн ) =U; U (0) = 0.

В левой лотереи есть выбор между действиями А (получить 1 млн.) и В (согласиться на лотерею). В экспериментах подавляющее большинство людей предпочитает А. Откуда следует

U > 0.1*1 + 0.89*U + 0.01*O или U > 10/11

В правой лотерее есть выбор между действиями С и D (две лотереи). Подавляющее большинство людей предпочитает действие С (почти та же вероятность проиграть, но выигрыш больше). Тогда

0.1*1 + 0.9*O > 0.11*U + 0.89*O т.е. U < 10/11.

Совершая такой выбор, люди действуют не в соответствии с функцией полезности. Полученный парадокс носит название парадокса Алле.

Рассмотрим ещё пример. Две лотереи, показанные на рис.3 имеют одинаковые средние цены.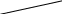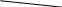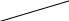

0,5 44

0,6 50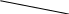




0,4 -20 0,5 0
Рис. 3. Сравнение 2-х лотерей
0.6*50 + 0.4* (-20) = 22

0.5*44 + 0.5 * 0 = 22.

Однако предъявление различным группам лотерей показало, что люди предпочитают правую лотерею, где при той же средней цене риск проигрыша исключен. Эти и другие примеры говорят о нерациональном поведении людей в задачах принятия решений.
5. Нерациональное поведение. Эвристики.
Один из наиболее известных примеров нерационального поведения людей – «дилемма генерала». Генерал потерпел поражение в войне и хочет вывести свои войска (600 чел.) с территории противника. У него есть две возможные дороги с возможными потерями при выборе каждой из них. Данные о дорогах и возможных потерях представлены на рис. 4.




200 чел. спасены

600 чел Р= 1/3 600 чел. спасены

Р= 2/3 0 чел. спасены
Рис. 4. Дилемма генерала
Большинство людей рассматривающих дилемму выбирают первую дорогу, стараясь избежать лотереи, когда в одном из исходов погибает весь личный состав соединения.

Но эта же дилемма была представлена используемым в ином виде (рис. 5.)




400 чел. погибнут

600 чел.

Р= 1/3 никто не погибнет

Р= 2/3 все 600 чел. погибнут


Рис. 5. Иное представление дилеммы генерала
Теперь уже большинство испытуемых выбирает вторую дорогу, т. к. на ней с вероятностью р = 1/3 можно спасти все соединение. Легко видеть, что лотереи на рис. 4 и 5 эквивалентны.

Эти и другие примеры демонстрируют отклонение поведения людей от рационального поведения, определяют эвристики, которые используются при принятии решений. Перечислим наиболее известные эвристики.
1. Суждение по представительности.

Люди часто судят о вероятности того, что объект А принадлежит к классу В только по похожести А на типовой объект класса В. Они почти не учитывают априорные вероятности, влияющие на эту принадлежность.

2. Суждение по встречаемости.

Люди часто определяют вероятности событий по тому, как часто они сами сталкивались с этими событиями и насколько важными для них были эти встречи.

3. Суждение по точке отсчета.

Если при определении вероятностей используется начальная информация как точка отсчета, то она существенно влияет на результат.

4. Сверхдоверие.

Людям свойственно чрезмерно доверять своим суждениям, особенно в случаях, когда они выносят суждения о прошлых событиях.

5. Стремление к исключению риска.

Люди стремятся исключить альтернативы связанные с риском.
6.Объяснения отклонений от рационального поведения.
Признание нерациональности человеческого поведения привело к поиску его причин, основными из которых являются:

-Недостаток информации у ЛПР в процессе выбора

-Недостаточный опыт ЛПР

-Стремление ЛПР найти решение, оптимальное с точки зрения совокупности критериев (целей), строго упорядоченных по важности, но он не может его найти

-Различие между объективно требуемым временем для реализации планов и субъективным горизонтом планирования ЛПР.

При анализе решений экономического выбора знание и учет нерационального человеческого поведения весьма важно. Существует и такое мнение, что рынок приучает к рациональности, что значительные отклонения от рациональности могут привести к разорению ЛПР.

Стремление учесть реальное поведение людей и приблизить теорию к жизни привело к появлению теории проспектов.
7. Теория проспектов.
Теория проспектов была разработана для того, чтобы учесть реальные черты человеческого поведения в задачах с субъективными вероятностными оценками.

Теория проспектов позволяет учесть три поведенческих эффекта:

1. эффект определенности, т. е. тенденцию придавать больший вес детерминированным исходам

2. эффект отражения, т. е. тенденцию к изменению предпочтений при переходе от выигрышей к потерям

3. эффект изоляции, т. е. тенденцию к упрощению выбора путем исключения общих компонентов вариантов решений.

Рассмотрим игру (x, p, y, q), где исход Х осуществляется с вероятностью p, исход Y – с вероятностью q, а нулевой исход – с вероятностью (1 – p – q), рис. 6. В теории проспектов игра, представленная на рис. 6, называется проспектом. Оценивается ценность (а неожидаемая полезность) этой игры по следующей формуле:

V = V(x)* П(р) + V(y)* П(q), где V(x), V(y) – ценность исходов x, y соответственно, V(0) = 0 и П(р), П(q) – вес (важность) вероятностей p, q соответственно.
p x

1 – p – q

0

q y
Рис. 6. Представление проспекта
Отметим некоторые отличия теории проспектов от теории полезности:

-Использование функции от вероятностей вместо вероятностей

-Полезность определялась как прибавление к первоначальному благосостоянию человека. Ценность же отсчитывается от любого уровня, принятого за - исходный.

-Для учета поведенческих аспектов предполагается, что функция V(x) ценности – выпуклая для выигрышей и вогнутая – для потерь

(Рис. 7.)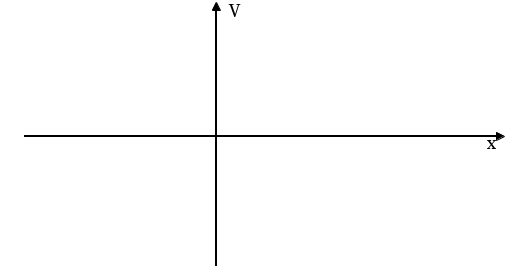



Рис. 7. Функция ценности V(x).
Функция вероятности П(р) построена специальным образом для учета поведенческих аспектов. Прежде всего П(р) не подчиняется всем законам теории вероятностей. Отметим следующие свойства П(р):

1. 
   П(0) = 0
   
2. 
   П(р) + П(1 – р) < 1
   
3. 
   При малых вероятностях П(р)>р
   
4. 
   Отношение П(р) / П(q) ближе к единице при малых вероятностях, чем при больших.
   
5. 
   П(р) плохо определена у крайних значений.
   

Покажем, что применение новой теории проспектов позволяет избежать парадокса Алле.

Из левой лотереи следует U > П(0,1) / 1 – П(0,89)

Из правой лотереи следует П(0,1) / П(0,11) > U

Или же П(0,1) / П(0,11) > U > П(0,1) / 1- П(0,89)

Так как из свойств функции П(р) вытекает возможность выполнения неравенства 1 – П(0,89) > П(0,11) и 1 > П(0,89) + П(0,11), то в теории проспектов парадокс Алле уже не имеет места.