Диплом. Научноисследовательская часть Технические требования
 Скачать 5.55 Mb. Скачать 5.55 Mb.
|
|
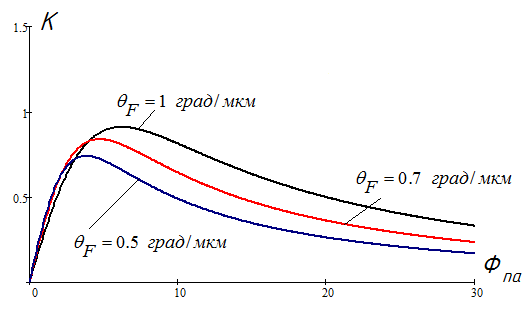
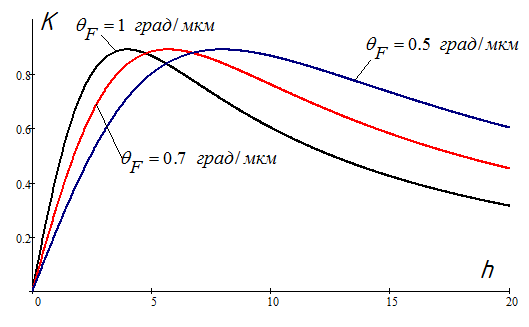
1.2.4. Сравнение выбранного магнитооптического метода с другими методами визуализации. Сравнение магнитооптического способа визуализации магнитной записи с другими, известными ранее, позволяет сделать выводы об определенных его преимуществах. Если сравнивать магнитооптический способ с порошковым, то оказывается, что последний сильно уступает по пространственному разрешению, редко достигающему величины 20 мкм. Магнитооптический метод более чувствителен и обеспечивает большую оперативность наблюдений при лучшем качестве изображения. Магнитооптический способ гораздо проще, чем способ визуализации, использующий пленки с полосовой структурой, который требует наличия дополнительных источников переменных и постоянных магнитных полей. Кроме того, неудобством является косвенный метод наблюдения – с помощью дифракции на частицах коллоида, ориентированных полосовой доменной структурой. Использование для визуализации метода, связанного с размягчением рабочего слоя носителя записи, приводит к необратимым повреждениям носителя и это резко ограничивает возможности его применения. Применение электронно-оптических методов, обладающих субмикронным пространственным разрешением, существенно ограничено их уникальностью и сложностью технической реализации. Использование для визуализации аморфных пленок, содержащих железо, позволяет достичь достаточной чувствительности и высокого пространственного разрешения. Но низкая эффективность отражательного магнитооптического эффекта Керра не дает возможности получить приемлемый для наблюдения контраст изображения. Результаты сравнения позволяют заключить, что по совокупности параметров – чувствительности, разрешающей способности, контрасту изображения, простоте и удобству пользования – магнитооптический способ визуализации магнитной записи обладает рядом преимуществ по сравнению с известными способами. 1.3. Математическое описание ОЭУРМ Для математического описания рассмотрим систему поляризатор-магнитооптический кристалл-анализатор и опишем происходящие процессы при помощи аппарата поляризационной оптики. 1.3.1 Поляризатор. Поляризатором называется оптическое устройство, преобразующее проходящий через него естественный свет в поляризованный. Поляризатор, предназначенный для обнаружения поляризации, называется анализатором. Действие поляризационных приборов основано на одном из физических явлений: а) на отражении и преломлении на границе двух диэлектриков (например, воздух – стекло); б) двойном лучепреломлении; в) на дихроизме (явлении различного поглощения o- и е- лучей). В данной работе в качестве поляризаторов применяются поляроиды Н-типа, работающие на дихроизме. Поляроидом Н-типа называют прозрачный плоский полимерный материал, который состоит в основном из полимерных молекул, имеющих преимущественное направление, и окрашен веществом, обеспечивающим дихроизм пленки [14]. Линейно поляризованный свет получается при прохождении света через поляроид. Поляроид сильно поглощает световые лучи, в которых электрический вектор перпендикулярен к оптической оси. Если же электрический вектор параллелен оси, то такие лучи проходят почти без поглощения. Поэтому естественный свет, пройдя через поляроид, наполовину поглощается и становится линейно поляризованным с электрическим вектором, ориентированным параллельно оптической оси поляроида [15]. Наиболее полным методом описания поляризатора является представление в виде 4Х4-матрицы Мюллера, состоящей из 16 действительных элементов. С помощью такой матрицы можно описывать любой поляризатор, независимо от того, вносит ли он, кроме поляризации, сдвиг фаз или рассеяние и состоит ли он из одного слоя или из многих слоев. Если рассеяние отсутствует, то можно применять 2Х2-матрицу Джонса. Метод Мюллера представляет собой матричное описание светового пучка и оптического устройства, через которое проходит свет, и позволяет вычислить результат взаимодействия света с этим устройством. Обычные методы становятся чрезвычайно громоздкими, когда число поляризаторов или фазовых пластинок велико. Преимущества метода Мюллера состоят в том, что он дает возможность: а) сконцентрировать все необходимое для описания пучка света параметры в едином выражении, б) записать в едином выражении все параметры поляризатора или фазовой пластинки и в) получить результат взаимодействия света с системой различных оптических элементов (поляризаторы, фазовые пластинки, рассеивающие устройства) путем простого перемножения соответствующих выражений по определенным правилам [16]. Пучок света описывается вектором Стокса, определяемым четырьмя параметрами I, M, C, S, которые связаны с интенсивностью. Этот вектор записывается обычно в виде вертикального столбца или в виде горизонтальной строки: 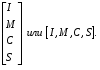 Параметр I называется интенсивностью, параметры M, C и S называются соответственно параметром преимущественной горизонтальной поляризации, параметром преимущественной поляризации под углом +450 и параметром преимущественной правоциркулярной поляризации. Когда параметр имеет отрицательную величину, это значит, что преимущественной является ортогональная форма поляризации. Матрица Мюллера поляроида записывается следующим образом: 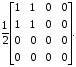 Однако, в более точном представлении поляроид представляет собой однородный нерассеивающий недеполяризующий недвупреломляющий поляризатор с главными значениями пропускания τ1=0,8 и τ2=0,0003 с горизонтальной осью пропускания, поэтому его матрица имеет вид: 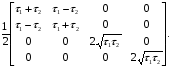 Если свет проходит три оптических устройства, необходимо использовать три матрицы и произвести три умножения. Если эти три матрицы обозначить через [M1], [M2] и [M3], а через [Vi] – вектор Стокса падающего света, то процедуру определения вектора Стокса [Ve] выходящего света схематически можно записать следующим образом: 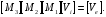 Таким образом, выпишем матрицы Мюллера для каждого оптического элемента и найдем вектор Стокса на выходе. 1.3.2 Магнитооптический кристалл Осуществляет модуляцию по амплитуде, вращает плоскость поляризации (модуляция поляризации) на определенный угол. Магнитооптические эффекты можно разделить на две основные группы: эффекты, наблюдаемы при прохождении света через магнитооптический материал, и эффекты, при отражении света от поверхности магнитооптического материала. В данной работе применяется эффект первой группы. Эффекты первой группы связаны с двойным круговым преломлением, т.е. с различием комплексных показателей преломления право- и левополяризованных по кругу волн. Действительная часть двупреломления описывает поворот плоскости поляризации, а мнимая его часть, - превращение линейно поляризованного излучения в эллиптически поляризованный. Если линейно поляризованную волну представить как сумму право- и лево- поляризованных по кругу волн, то первый из упомянутых эффектов будет связан с различием скоростей их распространения, а второй – с различием их коэффициентов поглощения. Если свет распространяется через магнитооптический материал параллельно вектору его намагниченности, то наблюдается магнитное круговое двупреломление, носящее название эффекта Фарадея. Эффект Фарадея пропорционален пути светового пучка в магнитоупорядоченной среде 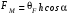 , ,где 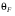 - удельное фарадеевское вращение; - удельное фарадеевское вращение; 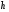 - длина пути в магнитной пленке феррит-граната, α – угол между направлением распространения излучения и вектором намагниченности М. - длина пути в магнитной пленке феррит-граната, α – угол между направлением распространения излучения и вектором намагниченности М.Таким образом, плоскость поляризации поворачивается на угол: 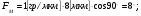 Магнитную пленку феррит граната можно представить, как фазовую пластину, описываемую матрицей Мюллера: 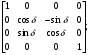 где 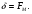 1.3.3 Анализатор. Анализатор – устройство, предназначенное для анализа характера поляризации света. В данной работе применяется линейный анализатор – служащий, для обнаружения линейно поляризованного света и определения угла наклона его плоскости поляризации. 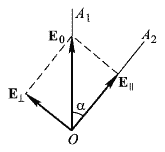 Рис. 1.14. Два поляроида поставлены друг за другом, так что их оси ОА1 и ОА2 образуют между собой некоторый угол α (рис. 1.14). Первый поляроид пропустит свет, электрический вектор Е0 которого параллелен его оси ОА1. Обозначим через I0 интенсивность этого света. Разложим Е0 на вектор Е||, параллельный оси ОА2 второго поляроида, и вектор Е┴, перпендикулярный к ней (Е0=Е||+Е┴). Составляющая Е будет задержана вторым поляроидом. Через оба поляроида пройдет свет с электрическим вектором Е  Е||, длина которого Е= Е0cos α. Интенсивность света, прошедшего через оба поляроида, будет Е||, длина которого Е= Е0cos α. Интенсивность света, прошедшего через оба поляроида, будет 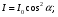 Закон Малюса – для любого поляризатора и анализатора. Матрица Мюллера имеет вид для анализатора тот же, что и для поляризатора, т.к. применяется точно такой же поляроид: 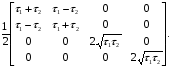 Нормированный вектор Стокса падающего света в данном случае представляет собой: 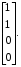 Теперь перемножим матрицы Мюллера и вектор Стокса: 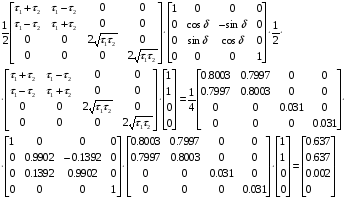 Итак, видно, что интенсивность в системе поляризатор-МОК-анализатор составляет 0.637 от интенсивности входного оптического сигнала. Интенсивность света I* на выходе МО прибора определяется следующим образом [1]: 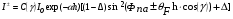 , , где C – коэффициент, учитывающий оптические потери в поляризаторе и анализаторе, а также потери на отражение I0 – интенсивность падающего на поляризатор излучения, 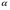 - коэффициент оптического поглощения МО среды, h– толщина пленки, - коэффициент оптического поглощения МО среды, h– толщина пленки, 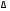 - коэффициент, учитывающий неполноту погасания в системе поляризатор – МО среда – анализатор, Фпа – угловое отклонение от положения погасания в системе поляризатор – анализатор, - коэффициент, учитывающий неполноту погасания в системе поляризатор – МО среда – анализатор, Фпа – угловое отклонение от положения погасания в системе поляризатор – анализатор, 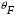 - удельное фарадеевское вращение, - удельное фарадеевское вращение, 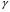 - угол падения излучения. - угол падения излучения.Контраст изображения Kопределяется следующим выражением 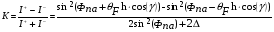 Оптическая эффективность η определяется по формуле 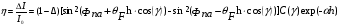 Приведенные графики зависимости K(Фпа) на рис.1.15 (при толщине пленки hравной 4 мкм), и K(h) на рис. 1.16 (при Фпа равным 5 град.) показывают, что контраст получаемого изображения определяется отклонением от положения погасания и достигает максимального значения при значении 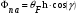 . .Максимальная чувствительность к управляющему полю достигается при 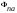 равной 45 град., при этом равной 45 град., при этом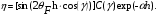
Для получения максимальной чувствительности толщина пленки определяется следующей зависимостью 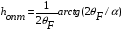 Оптический КПД тем выше, чем меньше оптическое поглощение и сильнее эффект Фарадея, другими словами, чем выше магнитооптическая добротность 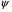 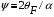 . .
Для того, чтобы выбрать наиболее подходящий материал магнитооптического кристалла для решения поставленной задачи, необходимо рассмотреть известные магнитооптические материалы и их основные характеристики. В настоящий момент самыми распространенными материалами для магнитооптических устройств являются: монокристаллические пленки феррит-гранатов, выращиваемые на подложках из немагнитных гранатов методом жидкофазной эпитаксии; ортоферриты; металлические аморфные пленки. 1.4.1 Феррит-гранаты 1.4.1.1 Кристаллическая структура и параметры решетки. Феррит-гранаты описываются общей формулой {ΣRi}3 [Fe, Me]2(Fe,D)3О12, где элементы в фигурных скобках соответствуют додекаэдрической, в квадратных — октаэдрической и в круглых — тетраэдрической подрешеткам граната; Ri – редкоземельные элементы: кальций, висмут, свинец; Me — элементы, замещающие железо в а-подрешетке (скандий, индий, титан, алюминий, галлий, свинец, редкоземельные элементы с малым ионным радиусом); D — элементы, замещающие железо в d-подрешетке (ванадий, кремний, герма¬ний, галлий, алюминий). Феррит-гранаты обладают структурой с кубической симметрией. Анионы кислорода образуют кубическую плотную упаковку, пустоты в которой заполняют меньшие по размерам катионы. Тетраэдрическую, октаэдрическую и додекаэдрическую подрешетки образуют катионы, окруженные четырьмя, шестью и восемью анионами кислорода соответственно. В одной формульной единице граната содержатся три додекаэдрические, две октаэдрические и три тетраэдрические позиции. Поскольку магнитооптически активный ион Bi3+ имеет большой радиус (параметр решетки гипотетического граната Bi3Fe5O12 равен 1,262 нм), при использовании традиционной подложки из Gd3Ga5О12 (ГГГ, аГГГ = 1,2383 нм) вместе с висмутом в состав МПФГ вводят элементы с малым ионным радиусом (Lu3+,Yb3+, Tm3+, Al3+, Si4+). В противном случае необходимы подложки с большим as, например Nd3Ga5O12 (НГГ, аНГГ = 1,2509 нм) или Sm3Ga5O12 (СГГ, асгг = 1,2436 нм). Однако НГГ и СГГ недостаточно прозрачны, поэтому было предложено использовать подложки (Gd, Ca)3(Mg, Zr, Ga)5O12 (ГКМЦГГ). Они прозрачны, как ГГГ, но as в них можно изменять от 1,2380 до 1,2560 нм путем варьирования содержания Са, Mg и Zr, получая при этом монокристаллы высокого качества с однородным распределением компонентов. Наиболее высококачественны подложки состава Gd2,67Ca0,33Ga4,03Mg0,32Zr0,65O12 с аs= 1,2495 нм [1]. 1.4.1.2 Оптическое поглощение. Беспримесные монокристаллы феррит-гранатов в области длин волн 1—6 мкм имеют окно прозрачности, где коэффициент оптического поглощения α очень мал (≤0,1 см-1). Однако в этом интервале могут присутствовать несколько узких пиков поглощения, связанных с электронными переходами в ионах R3+ в с-подрешетке (исключение составляют ионы Lu3+, Y3+, Gd3+ и La3+). В окне прозрачности поглощение определяется примесями и разного рода несовершенствами образцов. При λ<1 мкм поглощение в феррит-гранатах обусловлено электродипольными переходами в ионах железа. В области λ= 10÷100 мкм поглощение феррит-гранатов весьма интенсивно и связано с колебательным спектром молекул. При λ> 100 мкм вплоть до СВЧ диапазона феррит-гранаты обладают высокой прозрачностью, а уровень поглощения в них определяется дефектами кристаллической решетки. Для задач прикладной магнитооптики основной интерес представляют видимая и ближняя ИК области спектра. Пики поглощения, связанные с электронными переходами в редкоземельных ионах, присутствуют и в спектрах немагнитных гранатов (рис. 1.17), что ограничивает их применимость в качестве подложечных материалов. 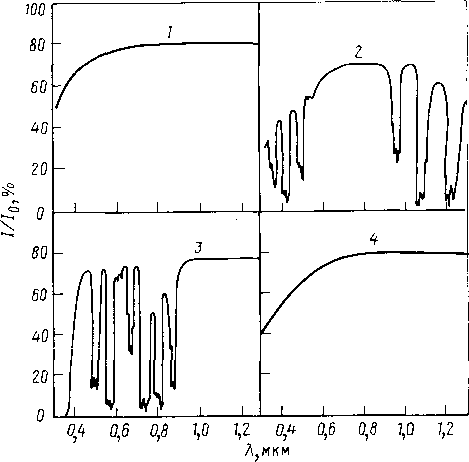 Рис. 1.17. Спектры пропускания ГГГ (1), СГГ (2), НГГ (3) и КНГГ (4) Спектры поглощения феррит-гранатов в видимом и ближнем ИК диапазоне определяются суперпозицией вкладов от внутриионных электродипольных переходов Fe3+ в кристаллическом поле с типичной силой осциллятора (пропорциональной площади соответствующего пика поглощения) f≈10-5 и значительно более интенсивных и широких переходов межионного типа с обменом заряда в области v>20 000 см-1 с типичной силой f≈10-3 (рис.1.17). 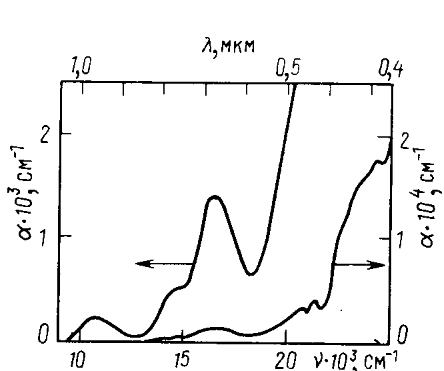 Рис.1.18. Спектр поглощения монокристалла Y3Fe3,85GA1,15O12 Внутриподрешеточные парные переходы в ионах Fe3+ и переходы с переносом заряда ответственны за оптическое поглощение в диапазоне λ≤0,45 мкм. В видимом диапазоне доминирующий вклад в а вносят два перехода в кристаллическом поле а- и d-подрешеток (рис. 1.18, 1.19). Эти переходы обусловливают поглощение, которое для беспримесного монокристалла Y3Fe5О12 составляет 620 см-1 при λ=0,633 мкм. Уменьшить это значение можно, лишь замещая железо диамагнитными ионами (рис. 1.19) . Однако при большом содержании таких ионов снижается обменное взаимодействие, что приводит к сильному изменению большинства магнитных и магнитооптических параметров. Введение в состав граната ионов магнитных переходных металлов либо вызывает появление новых переходов, либо влияет на переходы Fe3+, что в любом случае приводит к росту α. 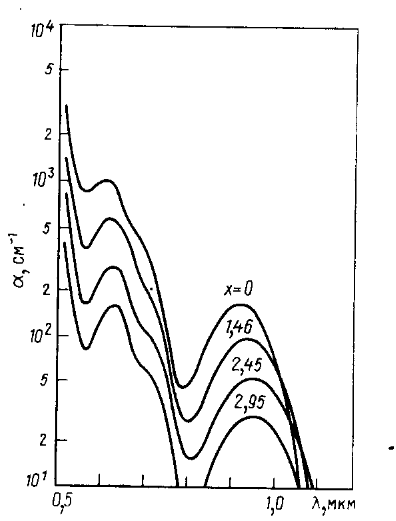 Рис. 1.19. Спектры поглощения МПФГ системы Y3Fe5-хGAхO12 при 295 К. Другим фактором, сильно влияющим на поглощение феррит-гранатов, является температура. С ее ростом край окна прозрачности смещается в область больших значений длин волн, что обусловлено двумя причинами: слабым смещением центра переходов в ИК область и уширением пиков поглощения (рис. 1.20), причем второй механизм доминирует. 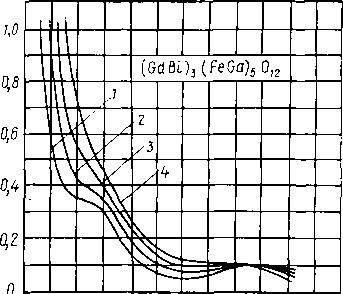 Рис. 1.20. Спектры поглощения МПФГ (Bi, Gd)3(Fe, Ga)5O12 при различных температурах, К: 1— 293; 2 — 373; 3 — 473; 4 — 573. |