Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73

• Название: Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
• Анкор: M_V_Bogdanovich_M_V_Kozak_Ya_A_Korol_metod.doc
• Дата: 03.02.2017
• Размер: 4.93 Mb.
• Имя файла: M_V_Bogdanovich_M_V_Kozak_Ya_A_Korol_metod.doc
• Тип: Навчальний посібник; #2000
• страница: 13 из 30

§24. Усне і письмове додавання та віднімання в межах 100 шд

Усне додавання двоцифрових чисел без переходу через десяток. Загальним прийомом усного додавання двоцифрових чисел є прийом порозрядного додавання. Його теоретичною основою є принципи десяткової системи числення та переставна і сполучна властивості дії додавання (сполучна властивість не формулюється). З'ясовується, що додавати або віднімати число можна частинами. Однак варто подати і проілюструвати на числових прикладах і таке правило: при додаванні кількох чисел їх можна переставляти, об'єднувати в групи, результат додавання від цього не змінюється. Можна також число розкладати на окремі доданки.

Методику опрацювання матеріалу подамо на основі фрагментів уроків.

Тема "Додавання двоцифрових чисел без переходу через десяток (загальний ішпадок: 34 + 52)".

Підготовчі вправи: а) кожне з чисел 55, 37, 71 і 17 запишіть як суму двох чисел за зразком: 49 = 40 + 9; б) користуючись переставною властивістю дії додавання, розв'яжіть приклади:

30 + 4 + 50 + 2; 70+1 + 20 + 8.

Пояснення нового матеріалу.

Будемо вчитися додавати двоцифрові числа. Нехай треба додати числа 24 і 73. Запишемо суму цих чисел і розкладемо кожне число на десятки і одиниці: 24 + 73 = 20 + 4 + 70 + 3.

Як зручно обчислити суму? Знайти спочатку окремо суми чисел 20 і 70 та 4 і З, а потім додати ці суми: 20 + 70 = 90; 4 + 3 = 7; 90 + 7 = 97. Отже, сума чисел 24 і 73 дорівнює 97. Розділ VII. Нумерація чисел 21-100. Арифметичні дії в межах 100

___.._ґ„^„^„,ичш ии в межах

Поясніть обчислення виразу 34 + 52, користуючись записами у підручнику.

34 + 52 = П



ЗО + 50 = 80 4 + 2= 6 80 + 6 = 86 Потім учитель пропонує пояснити обчислення виразу 43 + 24 за розгорнутим записом: 43 + 24 = 40 + 3 + 20 + 4 = 60 + 7 = 67.

Після обчислення двох-трьох виразів з використанням опорних записів учні обчислюють вираз 25 + 71 з усним коментуванням.

На основі розглянутих записів учитель формулює правило усного додавання двоцифрових чисел: додаючи двоцифрові числа, десятки додають до десятків, одиниці — до одиниць. Первинне закріплення.

Для закріплення учні обчислюють 6 — 8 виразів виду 55 + 13 і 1 — 2 задачі. Два приклади вони розв'язують з коментуванням, а решту — самостійно за двома варіантами. Задача має містити вивчені випадки дії додавання.

Наступний урок відводиться для розвитку вмінь виконувати додавання двоцифрових чисел без переходу через десяток. На цьому уроці можна запровадити коротке пояснення (без з'ясування розкладу на розрядні доданки). Подаємо зразок такого пояснення: 63 + 25; до числа 60 додати 20, буде 80; до числа 3 додати 5, буде 8; до числа 80 додати 8, буде 88; отже, 63 + 25 = 88. Щоб коментування відбувалося швидко, можна замість слова "додати" вживати слово "плюс" або сполучник "і".

Окремі випадки додавання (54 + ЗО; 54 + 3; 20 + 47; 2 + 47). До окремих випадків додавання належать такі суми, в яких в одному з доданків відсутні одиниці або десятки. За своєю сутністю тема продовжує формувати вміння застосовувати загальне правило додавання двоцифрових чисел. Наведемо зразки пояснень виконання обчислень.

54 + 30. У другому доданку немає одиниць. Отже, треба додати 50 і 30 і до знайденого результату додати 4: 50 + 30 = 80, 80 + 4 = 84.

54 + 3. У другому доданку: немає десятків. Отже, треба додати 4 і З, а результат додати до 50: 4 + 3 = 7; 50 + 7 = 57.

2 + 47. У першому доданку немає десятків. Отже, треба додати 2 і 7, а результат додати до 40: 2 + 7 = 9; 40 + 9 = 49.

При короткому поясненні не вказують, які розрядні одиниці відсутні, а відразу виконують дії. Наприклад, обчислення виразу 20 + 47 коментується так: 20 плюс 40 — шістдесят; 60 плюс 7 — шістдесят сім.

Застосування загального прийому до окремих випадків проводять на основі опорних записів, але у разі виникнення труднощів варто застосовувати предметне ілюстрування (бруски-десятки і окремі кубики, смужки з кружечками).

Методика викладання математики в початкових класах

151

На одному з уроків закріплення варто ознайомити учнів з прийомом послідовного додавання двоцифрового числа. На основі опорних записів їм пропонують пояснити і порівняти послідовність виконання таких обчислень:

26 + 63=[] 26 +- 63 = □

-^т 26+ 60 = 86' ■^іНЬ86 + 3 = 89 ^:1

20 + 60 = 80

6+3 = 9

80 + 9 = 89

Віднімання двоцифрових чисел без переходу через десяток. Теоретичною основою порозрядного віднімання двоцифрових чисел є правило віднімання суми від суми. У 2 класі це правило не вивчають. Пояснення подають за аналогією до прийому порозрядного додавання. Так, наприклад, прийом обчислення ілюструється предметними діями та відповідними записами. їх зміст відображено на мал. 89. 58 - 34 = []

50 - ЗО = 20; 8-4 = 4; 20 + 4 = 24

Десятки • Одиниці



Мал. 89

Після виконання двох операцій учитель ставить запитання:

Скільки десятків залишилось? Скільки одиниць залишилось? Яке число отримали?

Учням пропонують розглянути записи і пояснити обчислення. Потім формулюють правило: віднімаючи двоцифрові числа, десятки віднімаються від десятків, одиниці — від одиниць.

До окремих випадків віднімання належать такі різниці, в яких від'ємник не містить одиниць або десятків: 79 — 40, 79 — 2. Повідомлення теми можна зробити на основі таких вправ:

1. Від смужки завдовжки 36 см відрізали 2 см. Скільки сантиметрів становить довжина смужки? 2. Від смужки завдовжки 36 см відрізали 2 дм. Скільки сантиметрів становить довжина смужки?

Спочатку при поясненні вказуємо на особливість від'ємника.

79 — 40. У від'ємнику одиниць немає, треба відняти тільки десятки. 70 мінус 40 — тридцять; ЗО плюс 9 — тридцять дев'ять.

79 — 2. У від'ємнику немає десятків, треба відняти тільки одиниці. 9 мінус 2 — сім; 70 плюс 7 — сімдесят сім.

Згодом обчислення коментуємо без вказівки на особливість від'ємника.

На одному з останніх уроків закріплення варто ознайомити учнів з прийомом послідовного віднімання.

Розділ VII. Нумерація чисел 21—100. Арифметичні дії в межах 100



Методика викладання математики в початкових класах

153

Письмове додавання і віднімання двоцифрових чисел. Основна відмінність у виконанні письмового й усного додавання і віднімання полягає в тому, що усні обчислення починають з вищих розрядів, а письмові — з нижчих.

Для ознайомлення дітей з письмовим додаванням і відніманням застосовують метод пояснення. Можна використати нумераційну таблицю, в якій записані числа 28 і 45 (табл. 19).

Таблиця 19

Десятки	Одиниці
2	8
4	5
6	13
7	3

Учитель пропонує учню додати ці числа і записати результати додавання у нумераційну таблицю. Учень додає спочатку десятки, а потім одиниці, отримує 6 дес. і 13 од., записує це у нумераційну таблицю. Перевіривши записи, вчитель повідомляє, що десятки і одиниці додано правильно, але запис відповіді треба уточнити. 13 од. — це 1 дес. і 3 од. Треба 1 дес. зарахувати до десятків. Отже, відповідь буде така: 7 дес. і 3 од. Без нумераційної таблиці цей приклад можна записати так: ₊ 28 45_

73

Числа тут записано у стовпчик: одиниці під одиницями, десятки під десятками. Щоб відповідь не записувати двічі, додають спочатку одиниці, а потім десятки: 8 додати 5, буде 13. 13 — це 1 дес. і 3 од.; З од. пишемо під одиницями, а десятки додамо до десятків. 2 дес. плюс 4 дес, буде 6 дес. і ще 1 дес, буде 7 дес. Цифру 7 запишемо під десятками.

Додавання "стовпчиком" називають письмовим додаванням.

У ході закріплення учні виконують такі завдання:

1) Перевірте, чи правильно додали числа, записані в нумераційній таблиці, і поясніть, чому відповідь було записано двічі.

2) Прочитайте за підручником пояснення про письмове додавання.

3) Знайдіть суму двох двоцифрових чисел і поясніть обчислення. Учитель звертає увагу учнів на те, що при письмовому додаванні також

додають десятки до десятків і одиниці до одиниць, але починають додавання з одиниць.

На наступних уроках вводять коротку форму пояснення письмового додавання.

Знайти суму 47 + 29. Зразок короткого пояснення: 7 + 9 — шістнадцять, 6 пишу, 1 запам'ятовую; 4 і 2 — шість та ще 1 — сім, пишу 7, всього 76.;

+ ⁴⁷

л

76

Якщо вчитель не ставить вимогу дати повне пояснення, то учні користу­ються короткою формою пояснення.

Розглянемо пояснення письмового віднімання двоцифрових чисел з переходом через десяток.

Піднімання чисел можна також виконувати письмово. Від'ємник записують під зменшуваним так, щоб одиниці були під одиницями, а десятки під десятками. При письмовому обчисленні спочатку віднімають одиниці, (найдемо письмово різницю чисел 82 і 35. Запишемо числа стовпчиком. .■■-. мхї_82

■■•'■'Жо 35 '■■'

47

Пояснення. Від 2 од. не можна відняти 5 од. Беремо 1 дес. з 8 дес; 1 дес. І 2 од. — це 12. Від числа 12 відняти 5, буде 7. Запишемо цифру 7 на місце одиниць.

Від 7 дес. відняти 3 дес, буде 4 дес. Запишемо цифру 4 на місці десятків. Отримали число 47.

На наступному уроці учням подається зразок короткого пояснення письмового віднімання 86. _86

57

29

16 мінус 7, буде дев'ять, пишемо 9. 7 мінус 5, буде два, пишемо 2; всього 29.

Усне додавання з переходом через десяток. Усне додавання двоцифрових чисел з переходом через десяток виконуємо порозрядним додаванням. І Іаприклад, обчислюючи вираз 28 + 59, міркуємо так: 20 плюс 50, буде 70; 8 плюс 9, буде 17; 70 плюс 17, буде 87. З поданого зразка видно, що такий спосіб обчислення охоплює додавання круглих десятків, табличне додавання і переходом через десяток і додавання двоцифрового числа до круглого. З урахуванням цього і будують уроки на ознайомлення з новим матеріалом.

Додавання двоцифрових чисел з переходом через розряд розглядають у гакій послідовності: загальний випадок (наприклад, 28 + 59), окремі випадки ' пиду 38 + 4, 7 + 25, 42 + 8, 4 + 36, 36 + 54.

Розглянемо загальний випадок додавання виду 26 + 47.

Підготовчі вправи: а) обчисліть вирази і поясніть їх обчислення: 30 + 40; N І- 6; 80 + 19; б) обчисліть вирази, користуючись переставною властивістю дії додавання: 20 + 4 + 60 + 5; 30 + 8 + 20 + 9.

Розділ VII. Нумерація чисел 21—100. Арифметичні дії в межах 100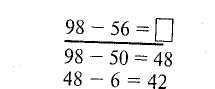



Методика викладання математики в початкових класах

153

Письмове додавання і віднімання двоцифрових чисел. Основна відмінність у виконанні письмового й усного додавання і віднімання полягає в тому, що усні обчислення починають з вищих розрядів, а письмові — з нижчих.

Для ознайомлення дітей з письмовим додаванням і відніманням застосовують метод пояснення. Можна використати нумераційну таблицю, в якій записані числа 28 і 45 (табл. 19).

Таблиця 19

Десятки	Одиниці
2	8
4	5
6	13
7	3

Учитель пропонує учню додати ці числа і записати результати додавання у нумераційну таблицю. Учень додає спочатку десятки, а потім одиниці, отримує 6 дес. і 13 од., записує це у нумераційну таблицю. Перевіривши записи, вчитель повідомляє, що десятки і одиниці додано правильно, але запис відповіді треба уточнити. 13 од. — це 1 дес. і 3 од. Треба 1 дес. зарахувати до десятків. Отже, відповідь буде така: 7 дес. і 3 од. Без нумераційної таблиці цей приклад можна записати так: ₊ 28 45_

73

Числа тут записано у стовпчик: одиниці під одиницями, десятки під десятками. Щоб відповідь не записувати двічі, додають спочатку одиниці, а потім десятки: 8 додати 5, буде 13. 13 — це 1 дес. і 3 од.; З од. пишемо під одиницями, а десятки додамо до десятків. 2 дес. плюс 4 дес, буде 6 дес. і ще 1 дес, буде 7 дес. Цифру 7 запишемо під десятками.

Додавання "стовпчиком" називають письмовим додаванням.

У ході закріплення учні виконують такі завдання:

1) Перевірте, чи правильно додали числа, записані в нумераційній таблиці, і поясніть, чому відповідь було записано двічі.

2) Прочитайте за підручником пояснення про письмове додавання.

3) Знайдіть суму двох двоцифрових чисел і поясніть обчислення. Учитель звертає увагу учнів на те, що при письмовому додаванні також

додають десятки до десятків і одиниці до одиниць, але починають додавання з одиниць.

На наступних уроках вводять коротку форму пояснення письмового додавання.

Знайти суму 47 + 29. Зразок короткого пояснення: 7 + 9 — шістнадцять, 6 пишу, 1 запам'ятовую; 4 і 2 — шість таще 1 — сім, пишу 7, всього 76_%

Якщо вчитель не ставить вимогу дати повне пояснення, то учні користу­ються короткою формою пояснення.

Розглянемо пояснення письмового віднімання двоцифрових чисел з переходом через десяток.

Піднімання чисел можна також виконувати письмово. Від'ємник записують під зменшуваним так, щоб одиниці були під одиницями, а десятки під десятками. При письмовому обчисленні спочатку віднімають одиниці, (найдемо письмово різницю чисел 82 і 35. Запишемо числа стовпчиком. .■■-. мхї_82

■■•'■'Жо 35 '■■'

47

Пояснення. Від 2 од. не можна відняти 5 од. Беремо 1 дес. з 8 дес; 1 дес. І 2 од. — це 12. Від числа 12 відняти 5, буде 7. Запишемо цифру 7 на місце одиниць.

Від 7 дес. відняти 3 дес, буде 4 дес. Запишемо цифру 4 на місці десятків. Отримали число 47.

На наступному уроці учням подається зразок короткого пояснення письмового віднімання 86. _86

57

29

16 мінус 7, буде дев'ять, пишемо 9. 7 мінус 5, буде два, пишемо 2; всього 29.

Усне додавання з переходом через десяток. Усне додавання двоцифрових чисел з переходом через десяток виконуємо порозрядним додаванням. І Іаприклад, обчислюючи вираз 28 + 59, міркуємо так: 20 плюс 50, буде 70; 8 плюс 9, буде 17; 70 плюс 17, буде 87. З поданого зразка видно, що такий спосіб обчислення охоплює додавання круглих десятків, табличне додавання і переходом через десяток і додавання двоцифрового числа до круглого. З урахуванням цього і будують уроки на ознайомлення з новим матеріалом.

Додавання двоцифрових чисел з переходом через розряд розглядають у кікій послідовності: загальний випадок (наприклад, 28 + 59), окремі випадки ' пиду 38 + 4, 7 + 25, 42 + 8, 4 + 36, 36 + 54.

Розглянемо загальний випадок додавання виду 26 + 47.

Підготовчі вправи: а) обчисліть вирази і поясніть їх обчислення: 30 + 40; N І- 6; 80 + 19; б) обчисліть вирази, користуючись переставною властивістю дії додавання: 20 + 4 + 60 + 5; 30 + 8 + 20 + 9. 154

Розділ VII. Нумерація чисел 21-100. Арифметичні дії в межах 100

Методика викладання математики в початкових класах

155

Пояснення нового матеріалу. Додавання двоцифрових чисел з переходом через десяток ми навчилися виконувати письмово. Проте такі числа треба вміти додавати усно. Знайдемо усно суму чисел 26 і 47.

26 /\

20 + 6

47

40 + 7

20 + 40 = 70 6 + 7 = 13 60 + 13 = 73

Запишемо суму в рядок і кожне число розкладемо на десятки й одиниці. Використовуючи переставну властивість, додамо спочатку десятки, а потім одиниці: 20 плюс 40, буде 60; 6 плюс 7, буде 13. Тепер додамо утворені суми: 60 + 13 = 73. Отже, сума чисел 26 і 47 дорівнює 73.

Після розгляду загального випадку учні можуть самостійно вказати способи обчислення окремих випадків додавання двоцифрових чисел з переходом через десяток.

Розглянемо випадок 38 + 4. У другому доданку немає десятків. Додамо число 4 до одиниць першого доданка. 8 + 4 = 12. Результат додамо до десяткін першого доданка: 30 + 12 = 42.

Зразок короткого пояснення: 8 і 4, буде 12; ЗО і 12, буде 42.

Після опрацювання окремих випадків можна ознайомити учнів :і прийомом послідовного додавання.

36 + 58 = П

/\

50 8

36 + 50 = 86 86 + 8 = 94

Усне віднімання з переходом через десяток. Порозрядне усне віднімання двоцифрових чисел з переходом через десяток потребує передбачення, що один десяток зменшуваного буде необхідний для віднімання одиниць від'ємника. Тому краще загальним прийомом вважати спосіб послідовного віднімання.

83-27 = []

83 - 20 = 63 63 - 7 = 56

Він спирається на вміння віднімати одноцифрове число від двоцифрового з переходом через десяток. Обчислення в цьому випадку можна виконати двома способами:

63-7 = П 63 - 7 = [] .■■;■

63 - 3 = 60 60 - 4 = 56

13-7 = 6 50 + 6 = 56

У класі розглядають обидва способи, але перевага надається першому.

Таким чином, загальному прийому віднімання передує ознайомлення учнів з випадками віднімання виду 40 - 8 і 63 - 7.

Віднімання виду 40 - 8 і 63 — 7 можна опрацювати методом пояснення, самостійно за записами та малюнком підручника, за допомогою стрічок з кружечками або за допомогою малюнка і пояснення до нього. Розглянемо спосіб обчислення 40 - 8 за малюнком підручника і за записами в ньому.

Нам треба навчитися віднімати одноцифрові числа від круглих десятків. У підручнику є опис послідовності віднімання, малюнок до нього і саме пояснення. Розгляньте їх і прочитайте пояснення (мал. 90). Розкажіть, як відняли 8 від 40.

40 - 8 = 32 /Ч 30 10

-.х>г.1О — 8 = 2.

щд ЗО + 2 = 32

40

Мал. 90

Після розгляду цих окремих випадків віднімання можна ознайомити учнів із загальним випадком віднімання двоцифрових чисел з переходом через десяток.

Тема "Віднімання двоцифрових чисел з переходом через десяток (загальний випадок 34 — 16)".

Підготовчі вправи:

63-20-3 45-10-5 91-40-1 63 - 20 - 7 45 - 10 - 9 91 - 40 - 6

Пояснення нового матеріалу. Знаходження різниці 34 - 16 на основі предметних дій з пучками-десятками і окремими паличками.

Утворимо число 34 з пучків-десятків і окремих паличок. Візьмемо 3 пучки-десятки і 4 палички. Нам треба відняти число 16, тобто відняти 1 дес. і 6 од. Піднімемо 1 пучок-десяток від 3 пучків-десятків, залишиться 2 пучки-десятки. ІЦе треба відняти 6 паличок. Віднімемо спочатку 4 палички. Залишиться тільки 2 пучки-десятки. Залишилося від 20 відняти 2; 20 - 2 = 18. Отже, 34 - 16 = 18..

Пояснення розв'язання за підручником' 84 - 29 = []

84-20 = 64 64 - 9 = 55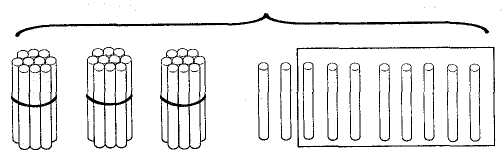



156

Розділ VII. Нумерація чисел 21-100. Арифметичні дії в межах 100

На кожний із розглянутих випадків додавання і віднімання та на закріп­лення в кінці теми присвячують 2—3 уроки. Частину часу уроків відводять для відтворення прийомів обчислень (коментоване розв'язування прикладів), але основним у роботі з формування навичок є застосування обчислюваль­них прийомів у різних ситуаціях.

Додавання і віднімання двоцифрових чисел з переходом через десяток для учнів важче, ніж без переходу через десяток. Тому не слід поспішати з обчисленням виразів на дві операції. Перші вирази на дві операції треба розв'язувати з коментуванням. Для закріплення необхідно добирати активні форми постановки завдань.