Навчальний посібник 3є видання, перероблене І доповнене тернопіль навчальна книга богдан ббк 74. 262. 2ІЯ73 Б73
 Скачать 4.93 Mb. Скачать 4.93 Mb.
|
§48. Розвиток просторових уявлень молодших школярів
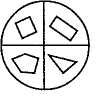
Бесіда. Якщо було 2 торбинки, то в них містилося 6 кг пшона. У скільки разів збільшилась кількість торбинок у другому стовпчику? (У 2 рази). Порівняйте, у скільки разів збільшилася кількість пшона у другому стовпчику? (У 2 рази). Порівняємо числа першого і третього стовпчиків. У скільки разів збільшилась кількість торбинок? (У 3 рази). А в скільки разів збільшилась кількість пшона? (Теж у 3 рази). Отже, у скільки разів збільшилась кількість торбинок, у стільки ж разів збільшилась і кількість пшона. Обернено пропорційна залежність. В обернено пропорційній залежності перебувають: ціна і кількість товару, час і швидкість руху, дільник і частка тощо. Розгляньмо розв'язання задачі, в якій величини перебувають в обернено пропорційній залежності. Задача. Для дитячого садка на 24 грн. закупили фарби для малювання ціною по 2 грн. за коробку. Скільки коробок фарб купили для дитячого садка ? Розв'язавши задачу,'доцільно з'ясувати з учнями, скільки можна купити за ці гроші коробок фарб, ціна яких у 2 рази більша, у 3 рази більша; звернути їх увагу на те, що при збільшенні ціни у два (три, чотири) рази кількість коробок фарб, які можна купити за 24 грн., відповідно зменшується у два (три, чотири) рази. Отже, при розв'язуванні задач з пропорційними величинами за допомогою відповідних запитань можна добитися певного уявлення учнів початкових класів про функціональну залежність. Використання буквеної символіки для узагальнення знань. Традиційно вважається, що в початкових класах учні розв'язують багато однорідних вправ, порівнюють їх, знаходять спільні ознаки, роблять висновки й узагальнення. Проте у навчанні молодших школярів узагальнення нерідко відбувається і на основі розв'язку одного-двох прикладів чи конкретної задачі, яка є прикладом певного виду задач. У такий спосіб учні ознайомлюються, зокрема, з алгоритмами арифметичних дій, з деякими новими видами задач. Методика викладання математики в початкових класах 289 При цьому найпростіший прийом узагальнення — заміна числових даних буквами. Буквене позначення компонентів і результатів арифметичних дій. Під час введення буквеного позначення компонентів бесіду здебільшого проводять на основі задачі. Наведемо зразок. Задача. У першій отарі 180 овець, а в другій — 210. Скільки всього овець удвох отарах? Як дізнатися скільки всього овець у двох отарах? (Треба додати числа 180 і 210). Замість чисел 180 і 210 можуть бути й інші числа. Якщо числа змінюються, то зручніше їх позначати буквами. Можемо вважати, що в першій отарі а овець, а в другій — Ь овець. Скільки овець тоді буде в обох отарах разом? {а + Ь). Якщо цю суму позначити буквою с, то отримаємо таку рівність: а + Ь = с. Як називаються числа а і 6? (Доданки). Як називається число с? (Сума). Сумою називають також і вираз: а + Ь. Подібні бесіди проводяться і для решти арифметичних дій: а — Ь с; а ■ Ь = с; а : Ь = с. У 3 класі узагальнюються випадки дій, пов'язаних з числами 1 і 0: а • 1 = а; а: а= 1; а : 1 = а; а + 0 = а; а - а = 0; 0 • а = 0; 0 : а = 0. Застосування тут буквеної символіки допомагає дітям давати правильні пояснення. Наприклад, для випадку а • 0=0: при множенні числа на нуль отримуємо нуль, тому 0-0 = 0. Буквене позначення зв'язків між компонентами і результатами арифметичних дій. У початковій школі опрацьовують задачі на знаходження невідомого компонента. Проте правила знаходження невідомих компонентів у підручниках не подано. Це пояснюється тим, що вчителі занадто вимогливо ставляться до заучування учнями правил напам'ять. Зрозуміло, що під час пояснення зв'язків учитель формулює правило, але не вимагає його заучувати. Зв'язки між компонентами і результатами дій широко використовуються для перевірки правильності обчислень. Розгляньмо одну з вправ з точки зору її узагальнювальної ролі. Закінчіть обчислення: 6-3=18 7 • 4 = 28 5 • 7 = 35 6 • 5 = 30 18:6 = 3 28:7 = 4 35:5 = * 30:5 = * Учитель з'ясовує, що отримаємо, коли добуток поділимо на один з множників, і робить узагальнення: "Якщо а ■ Ь = с, то чому дорівнює частка с : а? Частка с : ЬТ\ Вправа дає змогу учню самостійно сформулювати правило: частка від ділення добутку двох чисел на один з множників дорівнює іншому множнику. Такий підхід має певні переваги над заучуванням правила за підручником. Використання букв для запису властивостей арифметичних дій запроваджується в процесі вивчення дій у концентрі "Багатоцифрові числа". У більш систематизованому вигляді з цією метою буквена символіка подана в матеріалах для повторення у кінці року. В обох випадках буквені записи подаються після словесного формулювання властивостей. Це означає, що буквені записи виступають не як вищий рівень узагальнення, а як лаконічний290 РозділХШ. Пропедевтика алгебри в початкових класах засіб унаочнення властивостей. У підручнику в буквеному записі подано такі властивості: а + 6 = й + а — переставний закон додавання; а + Ь + с — а + (Ь + с) — сполучний закон додавання; а — (Ь + с), (а — Ь) — с — записи про властивість різниці, пов'язаної з різними способами обчислення зазначених виразів; а ■ Ь = Ь ■ а — переставний закон множення; а ■ Ь ■ с = а ■ (Ь ■ с) — сполучний закон множення; {а + Ь+с)-к=а-к+Ь-к+с-к — розподільний закон множення відносно додавання; с ■ (а — Ь) = с ■ а — с ■ Ь — розподільний закон множення відносно віднімання. З основними властивостями арифметичних дій у практичному плані учні мають справу неодноразово, тому їх буквене узагальнення не викликає ускладнень. Проте слід мати на увазі, що в кінці навчального року матеріал подається в довідково-описовому вигляді. Це матеріал для побудови вчителем зв'язної розповіді. Його не варто пропонувати учням для заучування. РОЗДІЛ XIV ПРОПЕДЕВТИКА ГЕОМЕТРІЇ В ПОЧАТКОВИХ КЛАСАХ Вивчення елементів геометрії розвиває просторові уявлення, образне мислення. Геометрична пропедевтика поділяється на такі складові: розвиток просторових уявлень молодших школярів, формування уявлень про лінії і відрізок, креслення і вимірювання довжин відрізків, ознайомлення з многокутниками, колом і кругом, вимірювання периметра і площ многокутників, спостереження геометричних тіл і введення їх назв. Мета вивчення елементів геометрії буде досягнута, якщо наприкінці навчання в початковій школі учні будуть орієнтуватися в основних напрямах положення і руху на площині і в просторі; знати найпростіші геометричні форми, пізнавати і знаходити їх у навколишньому середовищі; знати назви основних елементів фігур і деяких тіл, уміти їх показати і полічити; знати, якими поверхнями обмежена просторова форма простіших многогранників; вміти вимірювати довжину відрізків і креслити відрізки заданої довжини, знаходити довжину ламаної і периметр многокутника, вміти будувати прямокутники на папері в клітинку. Навчальна діяльність, в процесі якої діти оволодівають геометричним матеріалом, охоплює такі варіанти робіт: організоване вчителем спостереження різних геометричних форм і відношень; практика дітей у вимірюванні, побудові, конструюванні, малюванні; практика розв'язування задач з геометричним змістом. Через спостереження починається ознайомлення дітей з геометричними формами, їх істотними ознаками, положенням у просторі і на площині. Важливо, щоб учні не лише сприймали готові образи, що їх дає вчитель, а й самі відтворювали геометричні форми в процесі моделювання, креслення, вирізування, малювання. Тому центральне місце у формуванні геометричних понять займає практика самих школярів. §48. Розвиток просторових уявлень молодших школярів Сприймання простору передбачає сприймання відстані, на якій предмети розміщені від нас і один від одного, напряму, в якому вони перебувають, величини та форми предметів. Вправи з питань геометрії положення опрацьовуються в кожному класі початкового навчання, а найбільше їх у 1 та 2 класах. Серед вправ на розвиток просторових уявлень можна виділити кілька видів. Орієнтування в напрямах руху і в розміщенні предметів відносно самого себе. Орієнтування в напрямах руху і в розміщенні предметів охоплює такі поняття: вперед, назад, наліво, направо; вгору, вниз; спереду, позаду; зліва, справа. З цими поняттями діти ознайомлюються ще в дошкільному віці. У 1 класі їх потрібно уточнити й закріпити. Це роблять за допомогою різних292 Розділ XIV. Пропедевтика геометрії в початкових класах ігрових вправ, вправ під час проведення фізкультхвилинки, відповідних індивідуальних завдань. Подамо зразки вправ: 1. Назвіть два предмети, що знаходяться попереду від тебе (від учня); позаду від тебе; ліворуч від тебе; над тобою. 2. Опустіть руки вниз; праву руку підніміть вгору; витягніть руки вперед; ліву руку опустіть. Орієнтування в розміщенні частин предмета, розташованого перед суб'єктом. Порядкове розміщення предметів. Наведемо зразки вправ: 1. Прочитайте, які числа записані у правому стовпчику? У середньому стовпчику? У лівому стовпчику? (Мал. 149). 2. Які фігури накреслено у нижній половині круга? У правій половині? (Мал. 150).
 Мал. 149 Мал. 150 3. Покажіть верхній край дошки; лівий край дошки. Визначення положення, в якому знаходиться один предмет відносно іншого. Подамо зразки вправ: 1. Яка фігура на малюнку зліва? Яка справа? Яка посередині? (Мал. 151).  Мал. 151 2. Від чисел, записаних біля вершин квадрата, віщім: в середині квадрата (мал. 152). 10 8 11 9 Мал. 152 3. Назвіть точки, що лежать на прямій;ідазжшрямоіш(ядаи. 153). 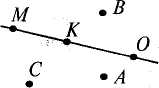 Методика викладання математики в початкових класах 293 Подібні вправи конкретизують, уточнюють такі поняття, як "вгорі — внизу", "нижче — вище", "зліва — справа", "над", "під", "в (всередині)", "поза", "між" тощо. Визначення положення предметів відносно певної особи. Порівняймо виконання двох вправ (мал. 154, 155). 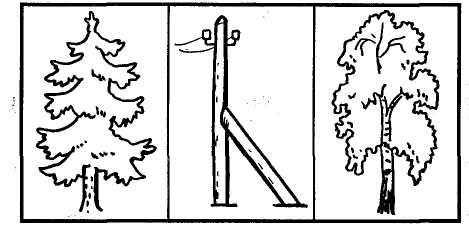 Мал. 154 Яке дерево зліва від стовпа? (Ялина).  Мал. 155 Яке дерево зліва від дівчинки? (Береза). (У цьому завданні краще міркувати, коли відповідає дівчинка: "Зліва від мене росте береза"). За відповідними малюнками зручно уточнити поняття: "наступний", "попередній", "останній" тощо. Наприклад, за малюнком до казки "Ріпка" можна поставити запитання: Хто стоїть попереду внучки? Хто позаду неї? Хто останній у цьому ряду? Хто перший? Хто наступний після Жучки? Хто попередній? Між ким стоїть бабка? Визначення горизонтального, вертикального і похилого положень. Подамо зразки вправ: 1) Візьміть олівець і розмістіть його в горизонтальному положенні, в похилому положенні, у вертикальному положенні.  294 Розділ XIV. Пропедевтика геометрії в початкових класах 2) Покажіть, який з відрізків на малюнку займає вертикальне положення, похиле положення, горизонтальне положення (мал. 156).  3) Накресліть відрізок у вертикальному положенні; похилому положенні. 4) Порівняйте, який відрізок довший: накреслений у вертикальному чи похилому положенні. Зрозуміло, що такі вправи застосовують і в подальшому навчанні математики, а також у наступних класах. §49. Формування уявлень про лінії і відрізки Крива і пряма лінії. Формування поняття про пряму і криву лінії можна почати показом спочатку обвислого, а потім натягнутого тонкого шнура. Учням варто запропонувати зігнути аркуш паперу довільної форми і в будь-якому напрямі. Розправивши цей аркуш, вони побачать, що на ньому утворилася пряма лінія. Тут можна сказати, що пряма лінія нескінченна, а бачимо ми лише її частину. Навчаючи дітей проводити прямі лінії за допомогою лінійки, вчитель спочатку демонструє виконання такої роботи на аркуші білого паперу, прикріпленого до класної дошки. Учні мають навчитися будувати вертикальну, горизонтальну і похилу прямі. Відрізок. Введення відрізка передує першим вправам на вимірювання довжини. Вчитель креслить на дошці пряму лінію і позначає на ній рисками дві точки. Він пояснює дітям, що частину прямої, обмежену двома точками, називають відрізком прямої або відрізком. Кінці відрізка на малюнку позначають тоненькими рисочками або точками. Якщо на малюнку рисочок (точок) немає, то це зображення прямої. Після ознайомлення з поняттям відрізка дітей вчать порівнювати їх за довжиною. Спочатку відрізки порівнюють "на око". При цьому вживають слова "рівні", "нерівні", "однакові", "довший", "коротший". Потім порівнюють за довжиною дві палички (дві смужки), прикладаючи їх одна до одної. У 1 класі вони ознайомлюються з мірами 1 см і 1 дм. Учні 2 класу оволодівають навичками побудови відрізків заданої довжини, розв'язування задач на знаходження довжини ламаної, обчислення периметра прямокутника. Вводиться нова одиниця вимірювання довжини — метр. Ламана лінія. Ламана лінія вводиться за такими малюнками підручника (мал. 157, 158). , ..л^,,^,^ ■ ,.«*■.■<* . .^ «ж. - ш>-- ■ Методика викладання математики в початкових класах 295   Мал. 157 Мал. 158 'Потій подається окрема ламана лінія (мал. 159) і ставиться заййтанняг зі скільквх-відрізків складено ламану лінію?  Мал. 159 У 3 класі вводять буквене позначення відрізків. Відрізки широко використовуються для розгляду понять збільшення і зменшення числа в кілька разів, кратного порівняння чисел та ін. У 4 класі вимірювання і креслення відрізків здебільшого пов'язані з розв'язуванням задач, зокрема задач на знаходження відстаней та на знаходження дробу від числа. Задача. Відрізок АВ становить 2/5 відрізка АС. Виміряйте довжину відрізка АС, а довжину відрізка АВ знайдіть обчисленням (мал. 160). Мал. 160 Креслення відрізків за масштабом. Як правило, такі завдання учні виконують під безпосереднім керівництвом учителя. Пояснення ведеться під час виконання вправ виду: /. Довжина накресленого на дошці відрізка А О дорівнює 8 дм. Побудуйте в зошиті зображення цього відрізка у зменшеному вигляді, припустивши, що 1 см відрізка в зошиті означатиме 1 дм відрізка на дошці. Скільки сантиметрів становить довжина накресленого в зошиті відрізка? У скільки разів відрізок на дошці довший, ніж відрізок, накреслений у зошиті? 2. Відстань між: містами дорівнює 70 км. Зобразіть цю відстань відрізком у зошиті, припустивши, що 1 см становить 10 км. Наведемо приклади завдань, в яких використовується поняття масштабу: 1. Відстань між двома населеними пунктами зображено відрізком КМ (мал. 161). Обчислітьцю відстань, взявши до уваги, що в 1 см вміщується 5 км. Мал. 161 296 Розділ XIV. Пропедевтика геометрії в початкових класах 2. Знайдіть відстані між Києвом та Вінницею і Києвом та Житомиром. Порівняйте відстані (мал. 162). Масштаб: в 1 см — 20 км. Київ — Вінниця . Мал. 162 §50. Ознайомлення з кругом і многокутником. Кути многокутника. Прямий кут. Прямокутник. Периметр многокутника Зміст роботи розкриємо окремо для кожного класу. У 1 класі учні ознайомлюються з трикутником, чотирикутником, п'ятикутником і шестикутником. Діти повинні засвоїти правильні назви цих многокутників, вміти їх розпізнавати. З цією метою многокутники, а також круг постійно використовуються як дидактичний матеріал. За програмою розгляд елементів многокутника у 1 класі не передбачено, але багато вчителів у ході аналізу того чи іншого многокутника пропонують показати і полічити сторони, вершини, кути. Таке випередження допустиме, але не слід його вводити в ранг програмових вимог. У процесі вивчення нумерації чисел першого десятка практикується складання многокутників з паличок, вирізування з паперу, а також розпізнавання многокутників на предметах оточення та малюнках. Новою вправою буде в цей час розгляд многокутника, поділеного відрізком на дві фігури, і визначення назви кожної фігури (мал. 163). Мал. 163 Робота з формування уявлень учнів про круг і многокутники проводиться в тісному зв'язку з уроками праці й образотворчого мистецтва. Діти складають фігури з паперу, малюють їх, використовують фігури для різноманітних аплікаційних робіт, малюють орнаменти з геометричними фігурами. У 2 класі продовжується робота з формування уявлень учнів про многокутники і круг. Пропонуються дещо ускладнені вправи на розпізнавання многокутників, на поділ фігур на многокутники і немногокутники. Учні вивчають елементи многокутників, вимірюють довжини їх сторін. Поняття кута і вершини трикутника (многокутника) вводять (конкретизують) за допомогою запитань: Скільки в трикутнику кутів? Вершин? Сторін? Методика викладання математики в початкових класах 297 Сторони, вершини і кути многокутника потрібно показувати учням на моделях плоских фігур. Кут бажано показати віялоподібним рухом указки, один кінець якої суміщений з вершиною кута многокутника. Треба звернути увагу дітей на те, що вершина многокутника є і вершиною відповідного кута. Бажано показати їм, що кути є різні за величиною, але величина кута не залежить від довжини його сторін. Прямий кут. Для ознайомлення з прямим кутом варто розглянути його утворення в процесі перегинання листка паперу. Кожному учневі треба дати аркуш паперу довільної форми. Потім під керівництвом учителя діти складають аркуші вдвічі, притискують лінію згину. Після цього аркуш перегинають ще раз, стежачи за тим, щоб частини утвореної раніше лінії перегину сумістилися. Утвориться кут. Такий кут називається прямим. Якщо папір розгорнути, діти побачать, що дві лінії перегину поділяють аркуш на чотири частини. Утворилось чотири прямі кути, які мають спільну вершину. За допомогою паперової моделі прямого кута учні відшукують прямі і непрямі кути на предметах з навколишнього оточення і на косинці. Після цього користуються прямим кутом косинця. Прямокутник. Дітям пропонують розглянути малюнки чотирикутників і знайти серед них такі, в яких всі кути прямі (мал. 164). Після цього подають означення прямокутника.  Мал. 164 Варто звернути увагу учнів на форму навколишніх предметів або їх частин. Вони знаходять предмети, що мають форму прямокутника: зошит, книжка, кришка стола, класна дошка тощо. У процесі вимірювання сторін прямокутника діти встановлюють, що його протилежні сторони рівні. Через кілька уроків вводять поняття довжини і ширини прямокутника. Квадрат. Квадрат вводять як рівносторонній прямокутник. Учитель пропонує серед даних на малюнку прямокутників або серед даних моделей знайти такі, в яких сторони рівні (мал. 165). Після цього він подає означення квадрата.  Мал. 165  298 Розділ XIV. Пропедевтика геометрії в початкових класах Із введенням понять прямокутника і квадрата збагачуються вправи на розпізнавання многокутників. Адже тепер квадрат має чотири назви: квадрат, прямокутник, чотирикутник і многокутник, а прямокутник — три назви: прямокутник, чотирикутник і многокутник. Наприкінці навчання в 2 класі запроваджуються вправи на розпізнавання многокутників у конфігураціях фігур. Коло і круг. При введенні поняття кола і круга можна йти двома шляхами: а) розглянути спочатку коло як особливий вид кривої лінії, а потім ввести поняття круга як фігури, яку обмежує коло; б) розглянути круг, виходячи з відомого дітям поняття "кружечок", а коло ввести як лінію, яка обмежує круг. У зв'язку з тим, що кружечки, вирізані з паперу, потрібні для проведення предметної лічби вже з перших уроків математики, перевагу варто надати другому шляху. Учитель повідомляє дітям, що на малюнку зображено круг (мал. 166). 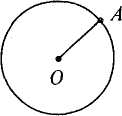 Мал. 166 Лінія, яка є межею круга, називається колом. Коло будують за допомогою циркуля. Точка О, в якій міститься голка циркуля,— центр кола. Відрізок ОА — радіус кола. З метою уточнення уявлень про коло і круг доцільно розглянути вправи виду: .С 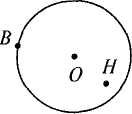 Мал. 167 Назвіть точки, які: а) належать кругу; б) належать колу; в) не належать у; г) належать кругу, але не належать колу (мал. 167). Навчаючи дітей креслити коло за допомогою циркуля, вчитель спочатку демонструє таку побудову на аркуші білого паперу, прикріпленому до дошки. При цьому він ознайомлює їх з інструкцією побудови кола за допомогою циркуля: 1. Розвести ніжку циркуля і вістря олівця на величину заданого радіуса. Для цього голку треба встановити на нульову поділку лінійки, а вістря олівця — на поділку, числове значення якої дорівнює заданій величині радіуса. 2. Встановити голку в задану точку. Для цього правою рукою потрібно тримати олівець, а пальцем лівої руки спрямовувати вістря голки в задану точку. 3. Коло креслять в напрямі за годинниковою стрілкою, нахиливши циркуль трохи вперед у напрямі руху олівця. Починати креслити слід від нижньої точки кола (від себе). Методика викладання математики в початкових-класах 299 4. Креслити коло треба однією правою рукою, тримаючи олівець за верхній кінець. 5. Лікоть правої руки спочатку відведений від корпуса, а відповідно до наближення вістря олівця до кінця (і початку) кола поступово наближається до нього. Спочатку учні вчаться будувати коло на окремих аркушах паперу (на чернетках). Коли вони більш-менш правильно навчаться креслити коло, можна дозволити побудову кола в зошиті. Є сенс і в тому, щоб ввести у 2 класі поняття діаметра кола. Вчитель пропонує дітям провести відрізок, який би проходив через центр кола і сполучав дві точки кола. Потім він повідомляє, що такий відрізок називається діаметром кола. Діаметр кола складається з двох радіусів. Він поділяє круг на дві рівні частини. Периметр многокутника. Означення периметра многокутника вводять у 2 класі. Як і довжину ламаної лінії, периметри многокутників знаходять у результаті вимірювання довжин їх сторін з подальшим додаванням здобутих результатів. У 3 класі вводять буквене позначення многокутників. Це дає змогу урізноманітнити постановку завдань з геометричним змістом. Наприклад, серед даних фігур назвати прямокутники, квадрати тощо. Пропонуються різні вправи на побудову многокутників на папері в клітинку. Причому такі завдання ускладнюють поділом фігури на задані многокутники. Учні продовжують виконувати вправи на знаходження периметра многокутника. При цьому їм потрібно показати різні способи обчислення. Якщо довжину прямокутника позначити буквою а, а ширину — буквою Ь, то ці способи можна записати так: а + Ь + а + Ь; а + а + Ь + Ь; а • 2 + Ь • 2; (а + Ь) • 2. Останній спосіб найзручніший, але учні повинні бути ознайомлені з усіма способами. У 4 класі діти продовжують виконувати вправи на розпізнавання і побудову плоских фігур, розв'язують інші задачі з геометричним змістом. Геометричні задачі, пов'язані з периметром, дещо ускладнюються, більшість з них пов'язана з поняттям площі фігури. Спостереження геометричних тіл і введення їх назв. Перші уявлення про геометричні тіла діти отримують у дошкільному віці. У початкових класах для розвитку цих уявлень можна використати уроки математики, малювання, а також моделювання з пластиліну на уроках праці, прогулянки та екскурсії. Можливі такі види роботи з геометричними тілами: розгляд предметів, моделей, малюнків, що мають певну геометричну форму; поступове введення назв геометричних тіл; знаходження в навколишньому середовищі предметів відповідної назви (форми); моделювання геометричного тіла з пластиліну; виділення деяких елементів тіла (вершини, ребра, грані, основи); малювання на папері за зразком і вказівками вчителя. У початкових класах варто дати школярам також поняття про такі геометричні тіла: кулю, куб, циліндр, прямокутний паралелепіпед, конус та піраміду. РОЗДШХУ ПОЗАКЛАСНА РОБОТА З МАТЕМАТИКИ Позакласна робота має бути невід'ємною частиною навчального виховного процесу. її головне завдання — виховувати інтерес до математики, стимулювати учнів до вивчення математики. У початковій школі доцільні насамперед ті види позакласної роботи, в яких можуть брати участь всі учні класу. З молодшими школярами практикуються такі види позакласної роботи: позакласні години з математики, конкурси на кращого математика, математичні екскурсії, математичні ранки, математичні олімпіади, математичні гуртки. За формою і змістом вони вміщують коротенькі бесіди (повідомлення), цікаві вправи на обчислення, парні та групові змагання, математичні ігри, розв'язування головоломок і задач, розпізнавання геометричних фігур та ін. |
