ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ: ЛІНІЙНІ СИСТЕМИ. Навчальний посібник для здобувачів ступеня бакалавра за освітньою програмою Інжиніринг автоматизованих електротехнічних комплексів
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
2. Знаходження передавальної функції розімкнутої системи, замкнутої системи по задаючому впливу та замкнутої системи по збурюючому факторуДля отримання передавальної функції розімкнутої систем WPC(s) складемо структурну схему розімкнутої САР. Для цього в структурній схемі: - діють всі впливи і ланцюги, прилеглі до них; - розривається головний ЗЗ (зворотній зв'язок), а її ланцюг є продовження прямої ланцюга проходження впливу g (рис. 2.1).  Рисунок 2.1 – Структурна схема розімкнутої САР Тоді можемо записати вираз для передавальної функції розімкнутої системи 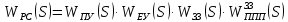 (2.1) (2.1)Для отримання передавальної функції замкнутої системи за допомогою одного з впливів скористаємося принципом суперпозиції. Структурна схема для отримання передавальної функції замкнутої системи по задаючому впливу представлена на рис. 2.2. 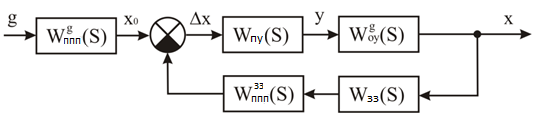 Рисунок 2.2 – Структурна схема САР по задаючому впливу Запишемо вираз передавальної функції як 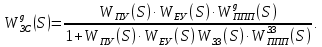 (2.2) (2.2)В рівнянні 2.2 можна відзначити, що чисельником передавальної функції є передавальна функція 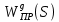 прямої ланцюга проходження сигналу g. Тому можна записати: прямої ланцюга проходження сигналу g. Тому можна записати: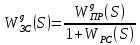 . (2.3) . (2.3)Структурна схема для отримання передавальної функції замкнутої системи по збурюючому фактору представлена на рис. 2.3.  Рисунок 2.3 – Структурна схема САР по збурюючому фактору Тоді вираз передавальної функції буде: 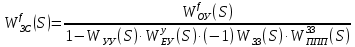 . (2.4) . (2.4)Або може бути представлено 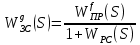 , (2.5) , (2.5)де 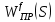 – передавальна функція прямої ланцюга проходження збурюючого фактору. – передавальна функція прямої ланцюга проходження збурюючого фактору.Структурна схема для отримання передавальної функції замкнутої системи за похибкою регулювання 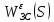 представлена на рис. 2.4. представлена на рис. 2.4. Рисунок 2.4 – Структурна схема САР за похибкою регулювання 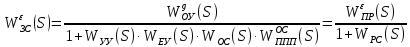 . (2.6) . (2.6)Аналізуючи рівняння (2.4)-(2.6), можемо зробити висновок, що передавальна функція замкнутої системи за допомогою одного з впливів Z дорівнює дробу 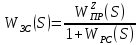 , (2.7) , (2.7)де 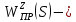 передавальна функція прямої ланцюга проходження сигналу Z. передавальна функція прямої ланцюга проходження сигналу Z.Отримані вирази передавальних функцій системи необхідно привести до двоповерхового дробу. 3. Аналіз систем автоматичного регулюванняСтудент повинен здійснити оцінку САР на стійкість до впливу збурюючих чинників за основними критеріями (кореневий характеристичного рівняння, Гурвіца, Михайлова та Найквіста). Основний режим будь-якої системи автоматичного керування (САК) – динамічний. При нормальній експлуатації автоматичні системи повинні підтримувати певний режим роботи об'єкта регулювання при дії на нього багатьох збурюючих факторів. Така поведінка може бути досягнута тільки в САК, що володіють стійкістю по відношенню до цих впливів. Стійкість системи означає, що малі зміни вхідного сигналу або будь-якого збурення початкових умов або установки не призведуть до значних відхилень вихідного сигналу. Таким чином, стійкість – це властивість системи повертатися у вихідний або близький до нього сталий режим після виходу з нього в результаті будь-якої дії. 3.1. Оцінка стійкості САР по кореню характеристичного рівняння системиПояснювальна частина. Отриману структурну схему САР (рис. 1.4) з відповідними передавальними функціями замкнутої системи по задаючому впливу 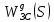 і збурюючому фактору і збурюючому фактору 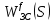 , можна зобразити як на рис. рис. 3.1. , можна зобразити як на рис. рис. 3.1.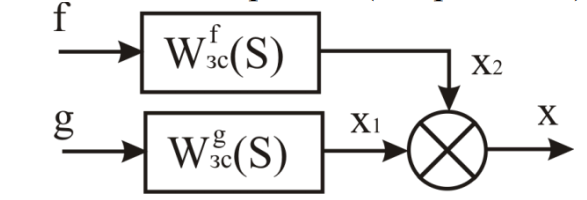 Рисунок 3.1 – Структурна схема САР із двома сигналами (задаючим та збурюючим) Рівняння вихідного сигналу САР з величиною S: 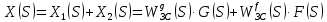 , (3.1) , (3.1)де G(S), F(S) – зображення задаючого g(t) впливу і збурюючого фактору f(t). Отже, щоб знайти перехідні процеси, що протікають в САР, необхідно застосувати до рівняння (3.1) зворотне перетворення Лапласа: 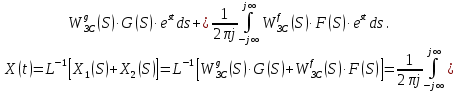 (3.2) (3.2)Для визначення перехідного процесу використовується формула Хевісайда: 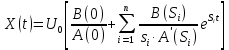 , (3.3) , (3.3)де 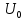 – амплітуда вхідного впливу; – амплітуда вхідного впливу; 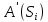 – значення похідної знаменника передавальної функції при відповідному значенні Siвсе; n – кількість коренів характеристичного рівняння системи. – значення похідної знаменника передавальної функції при відповідному значенні Siвсе; n – кількість коренів характеристичного рівняння системи.З рівняння (3.3) можна відзначити, що час t та корені характеристичного рівняння входять в показник експоненти. Корені характеристичного рівняння системи (рис. 3.2) можуть бути дійсними (корінь S1), комплексно- спряженими (S2 ,S3 ,S7 ,S8) та уявними (S5, S6). Крім того, корені можуть розташовуватися: в лівій півплощині, в правій або на осі ординат і, відповідно, будуть лівими, правими або нульовими. Система буде стійка, якщо перехідний процес при 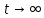 прямує до сталого значення X( прямує до сталого значення X(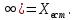 А це означає, що показник експоненти рівняння 3.3 має бути негативним, тобто всі корені характеристичного рівняння системи повинні розташовуватися в лівій півплощині Si-коренів (рис. 3.2). А це означає, що показник експоненти рівняння 3.3 має бути негативним, тобто всі корені характеристичного рівняння системи повинні розташовуватися в лівій півплощині Si-коренів (рис. 3.2).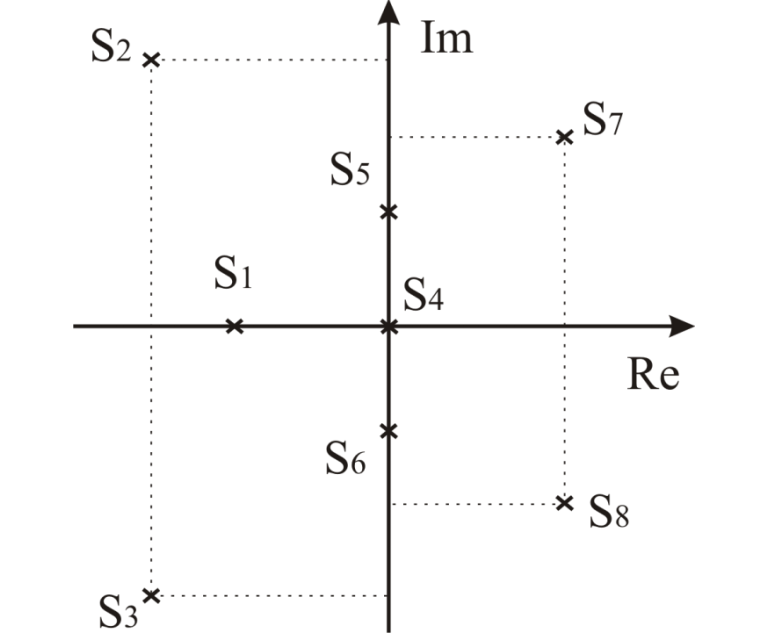 Рисунок 3.2 – Розташування Si-коренів характеристичного рівняння Для того, щоб САР була стійкою необхідно і достатньо щоб всі корені характеристичного рівняння системи були лівими. Якщо серед коренів характеристичного рівняння системи є хоча б один правий, а інші ліві, то САР є нестійкою. Приклад. Нехай передавальна функція замкнутої САР має вигляд: 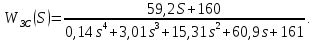 (3.4) (3.4)В програмному продукті MatLab, використовуючи функцію pole() отримаємо значення коренів характеристичного рівняння системи >> W=tf([59.2 160],[0.14 3.01 15.31 60.9 161]) Transfer function: 59.2 p + 160 ---------------------------------------------- 0.14 p^4 + 3.01 p^3 + 15.31 p^2 + 60.9 p + 161 >> pole(W) ans = –16.1139 –0.6350 + 4.1153i –0.6350 – 4.1153i –4.1160 Висновок. Так як всі корені характеристичного рівняння знаходяться в лівій півплощині, то система є асимптотично стійкою. 3.2. Дослідження стійкості системи за критерієм стійкості ГурвіцаПояснювальна частина. Критерій стійкості Гурвіца є алгебраїчним. Він формулюється так: якщо характеристичне рівняння системи має вигляд 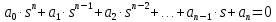 . (3.5) . (3.5)При чому а0>0, то для стійкості лінійної САР необхідно і достатньо, щоб були позитивні визначники Гурвіца і всі його діагональні мінори. Визначник Гурвіца є квадратною матрицею n- го порядку: 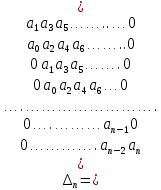 . .Перший рядок містить всі непарні коефіцієнти до останнього, після чого рядок заповнюється до необхідного числа елементів нулями. Другий рядок включає в себе всі парні коефіцієнти і теж закінчується нулями. Третій рядок формується з першої, а четвертий – з другої зміщенням вправо на один елемент. На місце, що звільнилося при цьому зліва, ставиться нуль. Аналогічно, зміщенням вправо на елемент утворюються всі наступні парні та непарні рядки з попередніх однойменних рядків. В результаті в головній діагоналі визначника виявляються послідовно записані всі коефіцієнти, крім а0. Критерій стійкості Гурвіца раціонально застосовувати для рівнянь не вище четвертої і п'ятої ступенів. Для рівнянь першого та другого ступенів необхідний критерій стійкості, що полягає у вимозі позитивності всіх коефіцієнтів рівняння, є і достатнім критерієм. Отже, умова стійкості полягає в наступному: 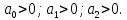 Для рівняння третього ступеня виду 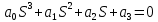 (3.6) (3.6)необхідно дотримуватися умови 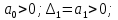 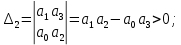 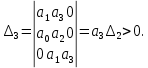 (3.7) (3.7)Отже, в цьому випадку потрібно не тільки позитивність всіх коефіцієнтів характеристичного рівняння, а й дотримання умови 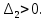 Аналогічно можна отримати умови стійкості для рівняння четвертого ступеня у вигляді вимоги позитивності всіх коефіцієнтів характеристичного рівняння і 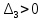 . Для рівняння четвертого ступеня: . Для рівняння четвертого ступеня:а0S4+а1 S3+а2 S2+а3S + а4=0; ао>0;а1>0; а2>0; а3>0; а4>0; а1 а2 а3 >а0 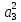 + +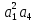 (3.8) (3.8)Для визначення значення критичного коефіцієнта ККР системи достатньо скористатися передостаннім визначником, і, прирівнявши його до нуля, знаходимо значення ККР. Приклад. Перевірити стійкість САР, що має характеристичне рівняння: S4 +8 S3+18 S2+16 S +5=0; 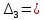 а1 а2 а3 – а0 а1 а2 а3 – а0 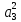 - -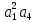 =8*18*16-1*16*16-8*5*5=1848>0; =8*18*16-1*16*16-8*5*5=1848>0;Ккр=1848. Система стійка. 3.3. Оцінка стійкості САР за допомогою критерію МихайловаПояснювальна частина. Цей критерій є частотним, і для оцінки стійкості САР необхідно отримати рівняння кривої Михайлова. Для цього скористаємося характеристичним рівнянням замкнутої системи (3.5). 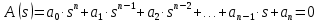 . (3.5) . (3.5)Переходемо в частотний діапазон. Для цього замінюємо Sj та виділяємо дійсну і уявну складові. Отримане рівняння кривої Михайлова матиме вигляд: 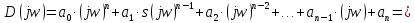 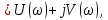 (3.9) (3.9)де U(ω), V(ω) – дійсна і уявна складові рівняння кривої Михайлова. Крива Михайлова будується за рівнянням (3.11) в комплексній площині (рис. 3.3). 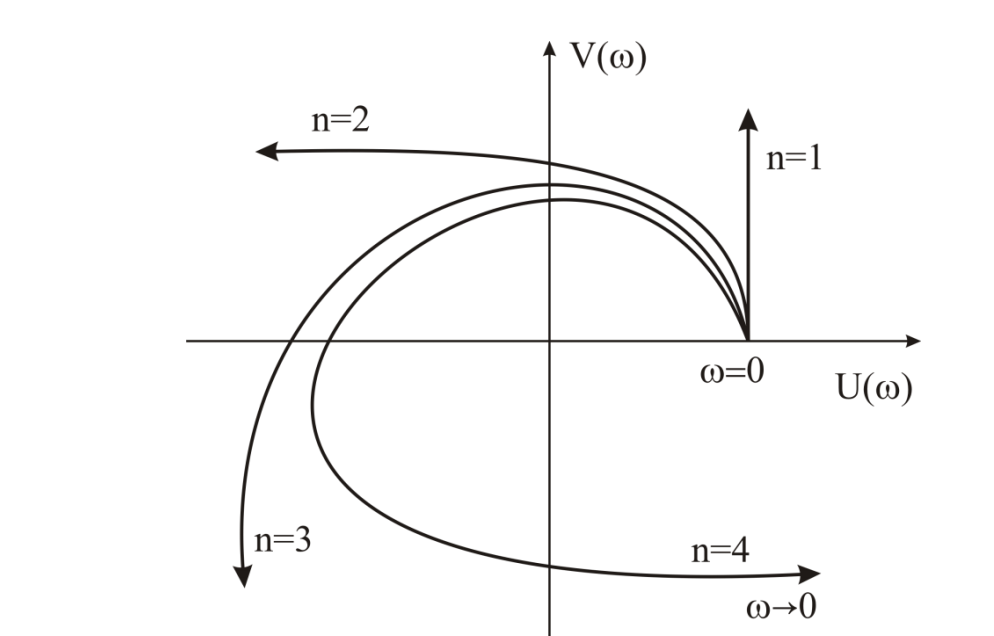 Рисунок 3.3 – Криві Михайлова, побудовані для n=1, n =2, n =3, n =4 Для того, щоб САР була стійкою необхідно і достатньо виконання наступних умов: - при 0 годограф кривої Михайлова повинен починатися з позитивної дійсній осі; - при зміні частоти 0 до годограф кривої Михайлова повинен: - почергово змінювати квадранти; - не проходити через нуль; - рухатись в позитивному (проти годинникової стрілки) напрямку; - пройти n квадрантів. Якщо годограф кривої Михайлова за відповідної частоти не дорівнює нулю, проходить через початок координат, то система є нейтральною. При невиконанні хоча б одного із сформульованих умов система є нестійкою. Приклад Запишем знаменник передавальної функції 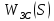 замкнутої системи із рівняння (3.4): замкнутої системи із рівняння (3.4):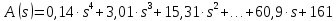 (3.10) (3.10)Зробимо заміну S=jw: 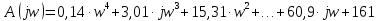 (3.11) (3.11)Розіб'ємо частотну характеристику на дійсну і уявну частини: 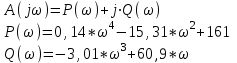 (3.12) (3.12)Використовуючи вбудовану функцію plot () в MatLab побудуємо годограф Михайлова і визначимо стійкість системи: >> w=0:0.01:10 >> p=0.14*w.^4-15.31*w.^2+161 >> q=-3.01*w.^3+60.9*w >> plot(p,q) >> grid 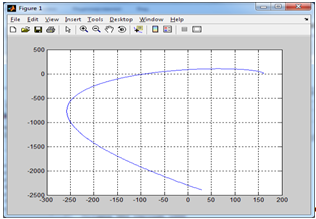 Рисунок 3.4 – Годограф Михайлова Виходячи з виду годографа Михайлова (рис. 3.4) видно, що система стійка, оскільки годограф починається на дійсній позитивної осі і проходить проти годинникової стрілки n-квадрантів, де n-порядок системи. В даному випадку n = 4. 3.4. Оцінка стійкості САР за допомогою критерію НайквістаПояснювальна частина. Цей критерій є частотним, і для оцінки стійкості САР необхідно скористатися передавальною функцією розімкнутої системи. Перейшовши в частотний діапазон (замінивши sj), необхідно побудувати годограф АФЧХ розімкнутої системи. Особливістю даного критерію є те, що по вигляду годографа АФЧХ розімкнутої системи оцінюється стійкість САР в замкнутому стані. Система автоматичного керування в розімкнутому стані може бути стійкою або нестійкою або нейтральною. Тому існує два підходи в оцінці стійкості системи. I. Підхід. Система в розімкнутому стані стійка. Якщо система в розімкнутому стані стійка, то для того, що б вона була стійкою і в замкнутому стані, необхідно і достатньо щоб годограф АФЧХ розімкнутої системи не охоплював точку з координатами [–1; j0]. Якщо годограф АФЧХ розімкнутої системи охоплює точку з координатами [–1; j0], то система в замкнутому стані є не стійкою. І, якщо годограф АФЧХ розімкнутої системи проходить через точку з координатами [–1; j0], то система в замкнутому стані є нейтральною, тобто знаходиться на межі стійкості. На рис. 3.5, 1 – САК в замкнутому стані є стійкою, для 2 – нейтральної, для 3 – нестійкою. 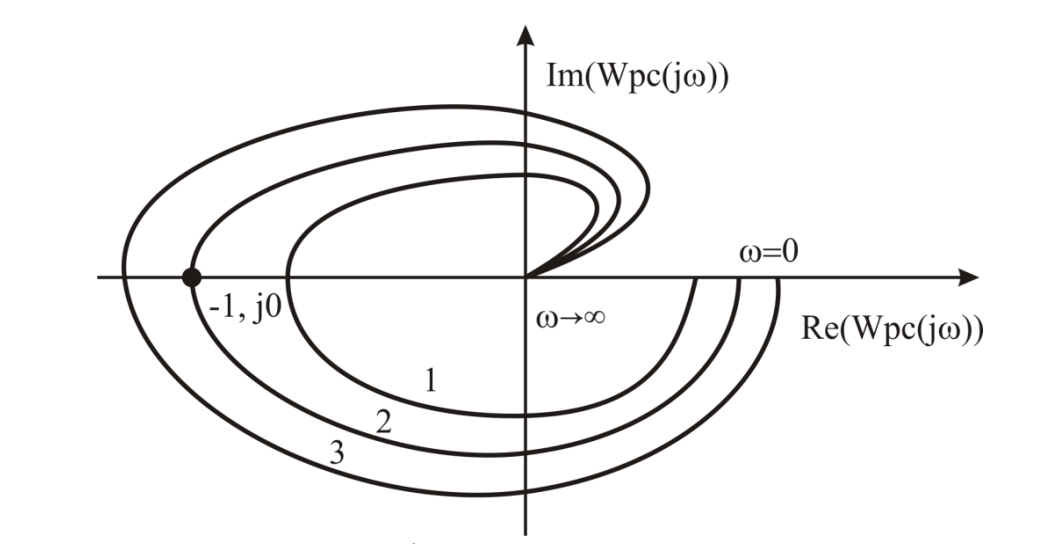 Рисунок 3.5 – Годографи АФЧХ розімкнутої системи II. Підхід. Система в розімкнутому стані є нестійкою або нейтральною. В даному випадку, в характеристичному рівнянні розімкнутої системи серед лівих коренів є хоча б один правий корінь або нульовий. Якщо система в розімкнутому стані є нестійкою або нейтрально, то для того, що б вона була стійкою і в замкнутому стані, необхідно і достатньо щоб годограф АФЧХ розімкнутої системи охоплював точку з координатами [–1; j0] в позитивному напрямку К/2 раз, де К – кількість правих чи лівих коренів. На рис. 3.6 зображений годограф АФЧХ нестійкої розімкнутої системи, яка має один правий корінь 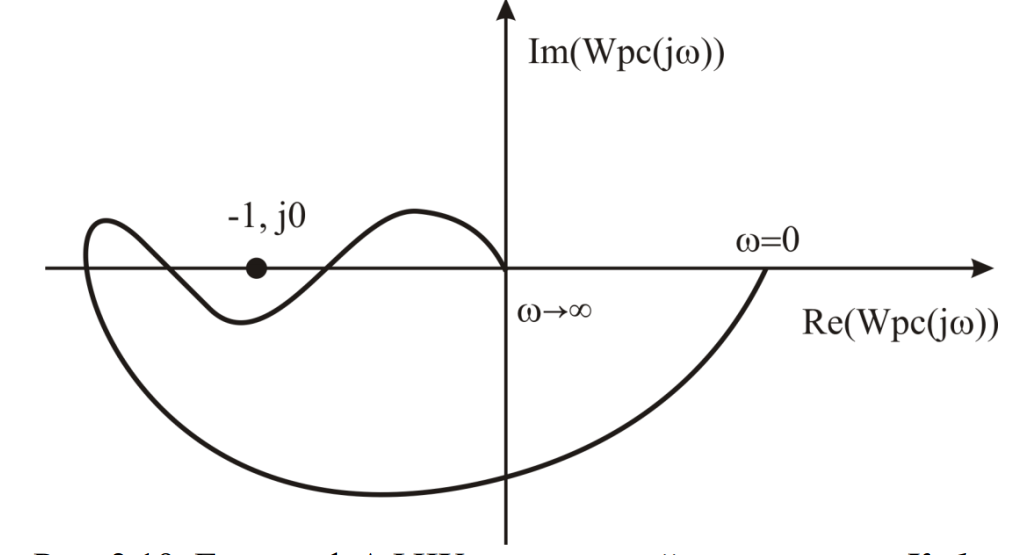 Рисунок 3.6 – Годограф АФЧХ розімкнутої системи при К=1 Годограф АФЧХ охоплює точку з координатами [–1; j0] в позитивному напрямку 0,5 рази, отже, система в замкнутому стані є стійкою. Приклад. Нехай передаточна функція розімкнутої системи: 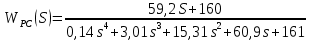 (3.13) (3.13)Використовуючи вбудовану функцію nyquist () в MatLab побудуємо годограф Найквіста і визначимо стійкість системи: >> W=tf([59.2 160],[0.14 3.01 15.31 60.9 161]) Transfer function: 59.2 p + 160 ---------------------------------------------- 0.14 p^4 + 3.01 p^3 + 15.31 p^2 + 60.9 p + 161 >> nyquist(W) 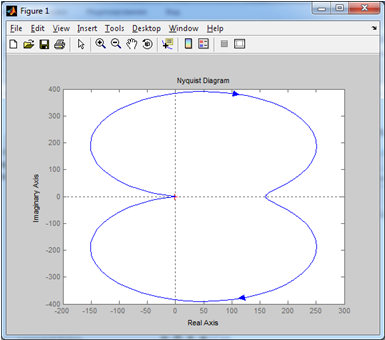 Рисунок 3.7 – Годограф Найквіста Так як на рисунку 3.7 не видно точки з координатою (–1; j0), тому важко оцінити стійкість системи. Для того щоб оцінити стійкість наблизимо годограф так, щоб було видно точку з координатою (–1; j0). 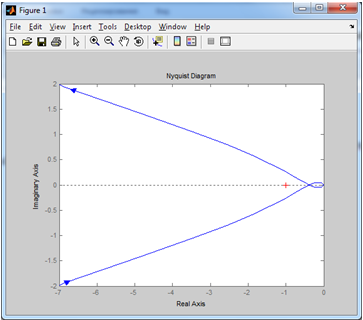 Рисунок 3.8 – Годограф Найквіста Так як годограф Найквіста (рис. 3.8) розімкнутої системи не охоплює точку з координатою (–1; j0), то замкнута система є стійкою. |
