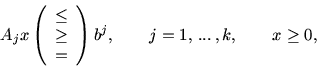Экономико-Матесатическое моделирование. Курсовая ЭММ. Несобственные оптимизационные задачи

• Название: Несобственные оптимизационные задачи
• Анкор: Экономико-Матесатическое моделирование
• Дата: 02.06.2022
• Размер: 476 Kb.
• Имя файла: Курсовая ЭММ.doc
• Тип: Курсовая; #566342
• страница: 2 из 6

1.2. Задача линейного программирования и ее экономическая интерпретация

Выпишем задачу ЛП в удобном для дальнейшего виде: 

(2.1)

здесь  ,  . Введя обозначения  ,  ,  , задачу (2.1) можно переписать в матричном виде 


Дадим экономическую интерпретацию этой задачи.

Пусть имеется некое производство, выступающее в качестве преобразователя   системы исходных ингредиентов   обладающих ценностью, в новую систему носителей ценности - совокупность продуктов. Термины производство, ценность, продукт, а ниже - оценка (как измеритель ценности) будут употребляться в качестве исходных.

Преобразуемыми ингредиентами могут быть: основные фонды и оборотные средства (оборудование, производственные площади, виды транспорта, сырье, электроэнергия и т.д.), природные ресурсы (полезные ископаемые, земля, воды рек и озер и др.), трудовые ресурсы, классифицированные по специальностям и уровню квалификации.

В основу преобразования ингредиентов положим некоторую конечную совокупность технологических способов, моделируемых векторами 



при этом координаты вектора p_i будем интерпретировать как затраты ингредиентов, приходящиеся на единичную интенсивность (например на единицу времени) использования i-го технологического способа. Саму же интенсивность обозначим через x_i (x_i =1 - единичная интенсивность).

Предположим, что затраты ингредиентов и создаваемая ценность подчиняются закону линейной зависимости от вектора интенсивностей  . В этом предположении затраты j-го ингредиента, отнесенные к вектору x, выразятся величиной  ,  . Так как границы сверху для них определены числами b_j, то должны выполняться неравенства 



Содержательный смысл вектора x, задающего уровень производства, диктует ограничение  . Таким образом, нами получена система ограничений задачи (1.1). Сказанное может быть подытожено схемой 



при этом  .

Если c_i понимать как оценку ценности, заключенной в носителе конечного результата применения i-го технологического способа с интенсивностью x_i=1, то величина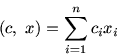 



будет выражать суммарную оценку ценности, заключенной в конечных носителях результата преобразования исходных ингредиентов в соответствии с уровнем производства, задаваемым вектором x.

Следовательно, задача (2.1) решает вопрос об отыскании уровня производства (вектора интенсивностей), подчиненного условиям технологической допустимости (формально - системе линейных неравенств) и доставляющего для   максимальное значение.

Возможна несколько модифицированная интерпретация задачи (2.1), а именно: пусть x_i - объем производства продукции i-го вида по i-му технологическому способу, c_i - цена реализации единицы продукции i-го вида. Тогда   выражает доход от реализации продукции, который максимизируется.

Остановимся на полезной интерпретации задачи ЛП в форме 

(2.2)

В основу положим перечень технологических способов   с интенсивностями   их использования; c_i - трудозатраты на единицу интенсивности x_i=1; b - вектор ресурсов; i-ый столбец p_i матрицы A - вектор затрат ресурсов, приходящихся на единичную интенсивность x_i=1; i-ый столбец h_i матрицы B - вектор выпуска продукции, приходящийся на единичную интенсивность x_i=1; d - зафиксированный уровень производства продукции. Модель (2.2) в введенных терминах читается так: отыскать уровень производства  , удовлетворяющий ресурсным ограничениям   и условиям на необходимый уровень производства продукции  , обеспечивающий минимум трудозатрат.

По существу, модель (2.2) и приведенная интерпретация (с возможностями расширения объема содержания введенных терминов) реализуют синтез требований и характеристик общеэкономического уровня, предъявляемых ко всякой естественной экономике. Положив M= 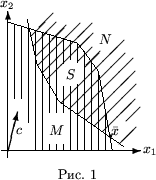 ,  , ситуацию модели (2.2) можно изобразить геометрически: см. Рис. 1.


 

На рисунке  ,   - вектор оптимального уровня производства, отвечающий направлению изображенного вектора c. Многогранники M и N выступают в качестве областей ''ресурсных возможностей'' и ''потребностей''. На практике, да и в общем смысле (в соответствии с аксиомами ''общества потребления''), многогранники M и N находятся в состоянии ''противостояния'', несогласованности, что можно выразить пустотой их пересечения:  .

Обобщением модели (2.2) в смысле задания структуры ее ограничений могла бы служить система неравенств 

(2.3)

где A_jx и b^j соединены одним из перечисленных отношений порядка. Это соответствует возможности как угодно полной структуризации всех участвующих в экономическом (производственном) процессе факторов, покрывающих области ресурсных, технологических и потребительских описаний. Детализация моделей типа (2.2) при ограничениях (2.3) приводит к различным классическим моделям математической экономики. В (2.3) отдельные блоки (т.е. подсистемы при различных j) могут не согласовываться (вступать в противоречие), т.е. при объединении давать несовместные системы. Такие ситуации соответствуют так называемым несобственным задачам линейного программирования.

1.3. Несобственные оптимизационные задачи

В данном пункте рассматриваются методы, использование которых позволяет найти выход из ситуации, когда задача определения плана производства в исходной постановке не имеет решения.

Несобственная (противоречивая) задача. Рассмотрим следующую модель: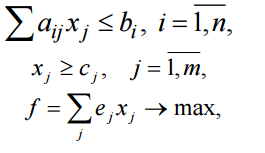



Считается, что для любого i существует >0, – величина спроса.

Функция цели имеет вид (3.3), где – эффективность выпуска j-го вида продукции. Если система ограничений (3.1) – (3.2) несовместна, то задача называется несобственной.

Метод минимизации невязок. В случае несовместности (несогласованности) ограничений необходимо скорректировать величины

(3.4)

где – снижение выпуска продукции относительно проектного задания. Система условий задачи планирования производства при ограничениях на выпуск продукции в виде (3.4) будет согласованной при любых значениях .

Функция цели в этом случае строится следующим образом. Определяется

, (3.5)

где – показатель, характеризующий снижение эффективности функционирования объекта планирования при уменьшении выпуска продукции по сравнению с величиной спроса. Затем из всех вариантов плана, которые обеспечивают минимум (3.5), выбирается тот, который максимизирует (3.3). При решении второй задачи в систему условий дополнительно вводится ограничение

, (3.6)

где y* – значение функции цели (3.5), полученное при решении задачи (3.5), (3.1), (3.4).

Использование метода штрафных функций позволяет получить численное решение сформулированных выше задач последовательной оптимизации в рамках одной задачи, функция цели которой имеет следующий вид: найти

, (3.7)

где r 0 – штрафной коэффициент.

Пример 1. Рассмотрим прокатный комплекс предприятия черной металлургии, включающий рельсобалочный стан, участок отделки фасонных профи- лей и термоямы. В термоямах обрабатывается продукция, требующая специальных режимов охлаждения. Номенклатура производимой продукции, удельные затраты времени работы оборудования (ч/тыс.т) и прибыль (млн руб./т), получаемая от реализации продукции, приводятся в таблице 3.1.

Таблица 3.1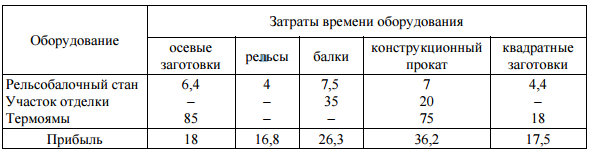



Фонд фактического времени работы оборудования (из календарного фонда исключается время ремонта и технологически неизбежных простоев при существующем уровне организации производства) в рассматриваемый период для всех участков составляет 7 тыс.ч. Согласно проекту планового задания необходимо произвести (тыс.т) как минимум: осевых заготовок – 55, рельсов – 1150, балок – 200, конструкционного проката – 5. Что касается квадратных заготовок, то их производство должно точно соответствовать проекту планового задания – 125 тыс.т. Предположим, что фонд фактического времени работы всех видов оборудования задается точно и определяет максимально допустимый уровень загрузки агрегатов. Необходимо определить вариант плана, максимизирующий эффективность функционирования рельсобалочного комплекса. Введем обозначения: x1 – объем производства осевой заготовки, x2 – объем производства рель- сов, x3 – объем производства балок, x4 – конструкционный прокат, x5 – квадратные заготовки. Ограничения, лимитирующие использование оборудования, будут записываться в виде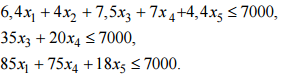



Приведем ограничения на выпуск продукции, а также функцию цели для рассматриваемого здесь варианта. Все переменные неотрицательны. Считается, что приоритетность выполнения проектных показателей одинакова.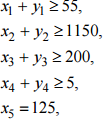





Производство в заданных пропорциях. Требованию пропорциональности в выпуске продукции различных видов отвечает следующая форма представления ограничений

(3.8)

При этом максимизируется доля z выполнения задания при заданной структуре спроса. Для рассматриваемого примера 1 ограничения на выпуск продукции и функция цели имеют вид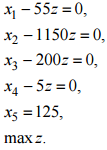



Возможность сбыта сверх комплектов. Условиями (3.8) пропорции в выпуске продукции задаются жестко, что не позволяет сбалансировать плановую программу с ресурсными возможностями объекта планирования. К тому же жестко задаваемые соотношения в выпуске продукции не всегда экономически оправданны. Ряд причин приводит к тому, что рациональные пропорции имеют некоторый допустимый интервал варьирования, т.е. возможны выпуск и реализация продукции сверх комплекта. Поэтому ограничения на выпуск дефицитных видов продукции записываются обычно в виде

(3.9)



где Mj – максимально допустимый выпуск продукции, определяемый рациональными потребностями.

При таком подходе функция цели имеет вид

. (3.10)

Для рассматриваемого примера 1 ограничения на выпуск продукции и функция цели имеют вид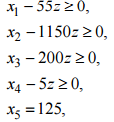





Рациональное использование ресурсов. Предложим иную запись условий, обеспечивающих более тесное приближение к величинам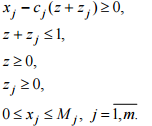

^(3.11)

Ограничения на ресурсы записываются в виде (3.1). Функцию цели бу- дем строить следующим образом. При последовательной оптимизации сначала максимизируется равномерное (пропорциональное cj) приближение к проекту планового задания по всем видам продукции (max z). Затем производится последующее «подтягивание» выпуска продукции до величин cj:



где pj – величины, характеризующие приоритетность выполнения проектных показателей cj. Лишь после этого исследуется возможность выпуска дефицитных видов продукции сверх проектного задания:



Такой метод обеспечивает рациональное использование ресурсов. Ис- пользование метода штрафных функций дает принципиальную возможность получения численного решения сформулированной трехэтапной задачи последовательной оптимизации рамках одной задачи, функция цели которой имеет вид

, (3.13)

где – штрафные коэффициенты, позволяющие реализовать процедуру последовательной оптимизации.

Данной схеме моделирования присущ тот недостаток, что в процессе ее применения мы отклоняемся от исходных пропорций в выпуске продукции, задаваемых величинами c j . Причем при использовании соотношений (3.11) отклонения будут меньшими. Однако эти схемы имеют и неоспоримое достоинство: полнее используются ресурсы и в большей мере обеспечивается достижение проектных показателей по выпуску продукции. Для рассматриваемого примера 1 ограничения на выпуск продукции и функция цели имеют вид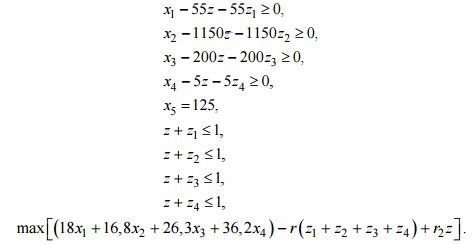