Экономико-Матесатическое моделирование. Курсовая ЭММ. Несобственные оптимизационные задачи

• Название: Несобственные оптимизационные задачи
• Анкор: Экономико-Матесатическое моделирование
• Дата: 02.06.2022
• Размер: 476 Kb.
• Имя файла: Курсовая ЭММ.doc
• Тип: Курсовая; #566342
• страница: 3 из 6

1.4. Двойственность для несобственных задач линейного программирования 

Под собственной задачей МП понимается разрешимая задача МП, для которой двойственная также разрешима и оптимальные значения этих задач совпадают. В противном случае задача называется несобственной (НЗ). В частности, если система ограничений в задаче неразрешима (противоречивая), то задача - несобственная. В случае задачи ЛП несобственность и неразрешимость - понятия эквивалентные. Если   и   - допустимые множества для пары взаимно двойственных задач ЛП, то непустота M и   соответствует разрешимости этих задач. В случае неразрешимости L (следовательно, и  ) возможны три альтернативы:

1)  - НЗ ЛП 1-го рода,

2)  - НЗ ЛП 2-го рода,

3)  - НЗ ЛП 3-го рода.

Причины и обстоятельства, порождающие неразрешимость модели, разнообразны. Это, в частности: неадекватное моделирование, противоречия между целями и ресурсными возможностями их достижения (находящие свое отражение в модели), перегруженность требований к объекту моделирования (например, к конструкции самолета), некорректность постановки (в смысле некорректности по Тихонову), противоречия между технологиями и средой (''грязные'' технологии и требования экологии) и т.д.

При автоматизированном (программном) формировании модели трудно разобраться в причинах несобственности, особенно тогда, когда этому фактору нужно придать содержательную интерпретацию и дать соответствующее объяснение. В случае задачи малой размерности, когда она хорошо просматривается, ситуацию неразрешимости можно преодолеть путем коррекции модели простыми средствами (проверить правильность исходных данных, ослабить некоторые ограничения или совсем их выбросит из модели и т.д.) и тем самым придти к разрешимой модели. В случае модели высокой размерности (число ограничений и переменных - тысячи и десятки тысяч) требуются более изощренные средства, причем программно обеспеченные. Для реализации такого подхода уже требуются теоретические наработки, в частности, теория двойственности, являющаяся мощным генератором конструктивных средств всестороннего анализа оптимизационных моделей. В основе двойственности для НЗ ЛП лежит схема:



В ней 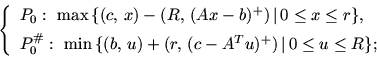 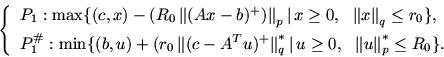 означает переход (сопоставление) задачам L и L^* по единому правилу   к разрешимым задачам P и P^*, обладающих свойствами: (P#)# = P и  P =  P#. Примерами реализаций Схемы 2 могут служить: 




Здесь R и r - неотрицательные векторные параметры,   - положительная срезка вектора  , R₀ и r₀ - неотрицательные числовые параметры,   и   - произвольные нормы в соответствующих пространствах,   и   - им сопряженные нормы.

Приведем более общую реализацию приведенной схемы. Пусть 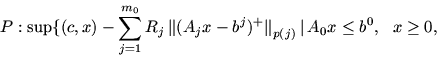 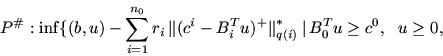   и     - произвольные разбиения систем   и   на подсистемы (в предположении, что подсистемы  ,   и  ,   - совместны); {b^j}, {u^j}, {cⁱ}, {xⁱ} - разбиения векторов   на подвекторы, соответствующие указанному разбиению. В принятых обозначениях задачи P и P# могут быть записаны следующим образом: 









Теорема 4.1   1). Пусть  ,     и задача P разрешима. Тогда   разрешима и    . 
2). Если   и   допустимы для P и P# соответственно, то  , где f(x) и f#(u) - функции, оптимизируемые в P и P#. Отсюда следует: если  , то  ,  .

З а м е ч а н и е 4.1. Все нормы, фигурирующие в написании задач P и P#, предполагаются монотонными.

З а м е ч а н и е 4.2. Справедлив и обратный вариант теоремы.

З а м е ч а н и е 4.3. Решение задач P и P# сводится к решению следующей системы линейных и выпуклых неравенств: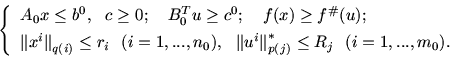