вар. 58. Обобщите результаты оценивания параметров модели и результаты проверки модели на адекватность

• Название: Обобщите результаты оценивания параметров модели и результаты проверки модели на адекватность
• Дата: 10.06.2022
• Размер: 281 Kb.
• Имя файла: вар. 58.doc
• Тип: Документы; #584508
• страница: 2 из 3

Как следует из данных, полученных с помощью Excel методом наименьших квадратов, полученная многофакторная модель будет иметь вид:

Y = -1046,49 + 2,0334∙X1 + 1828,83∙X2 (1.1)

(t) (-2,311) (6,181) (3,265)

Уравнение (1.1) выражает зависимость валового внутреннего продукта (Y) от экспорта товаров и услуг (Х1), обменного курса евро к национальной валюте (Х2). Коэффициенты уравнения показывают количественное воздействие каждого фактора на результативный показатель при неизменности других. В нашем случае валовой внутренний продукт увеличивается на 2,033 ед. при увеличении экспорта товаров и услуг на 1 ед. при неизменности показателя обменного курса евро к национальной валюте; валовой внутренний продукт увеличивается на 18,288 ед. при увеличении обменного курса евро к национальной валюте на 1 ед. при неизменности показателя экспорта товаров и услуг. Случайное отклонение для коэффициента при переменной Х1 составляет 0,329; при переменной Х2 – 5,601; для свободного члена –452,86. Помощь на экзамене онлайн.

Табличное значение критерия Стьюдента, соответствующее доверительной вероятности  = 0,95 и числу степеней свободы v = n – m – 1 = 29; t_кр. = t_0,025;29 = 2,364.

Сравнивая расчетную t-статистику коэффициентов уравнения с табличным значением, заключаем, что все коэффициенты уравнения регрессии будут значимы, за исключением свободного члена в уравнении регрессии.

Коэффициент детерминации R² = 0,8099;

Скорректированный на поте­рю степеней свободы коэффициент множественной детерминации AR² = 0,7968;

Критерий Фишера F = 61,766;

Уровень значимости модели р < 0,0000;

Согласно критерию Фишера данная модель адекватна. Так как уровень значимости модели меньше 0,00001.

Проверим остатки на наличие автокорреляции. Для этого найдем значение статистики Дарбина-Уотсона.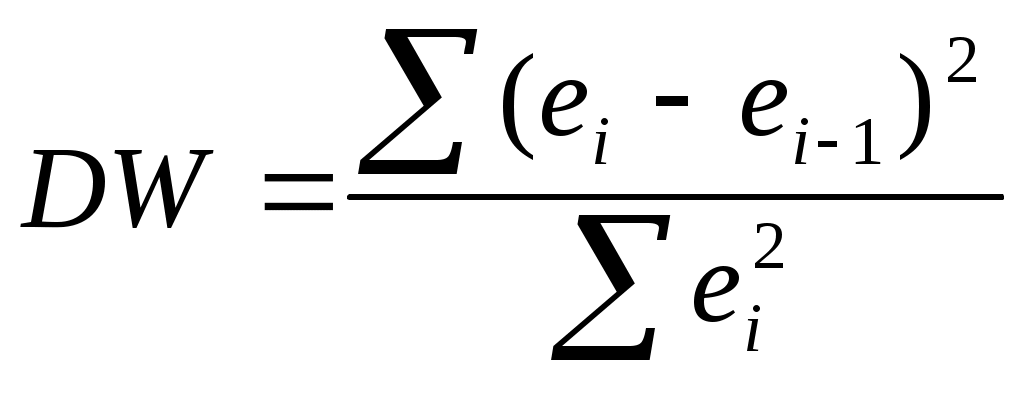


Промежуточные расчеты поместим в таблицу 1.4.

Таблица 1.4.

Остатки	et2	(et - et-1)2
218,5906	47781,84	0
195,5567	38242,44	530,5579
67,01115	4490,494	16523,97
263,2028	69275,71	38491,16
-93,1291	8673,038	126972,4
-39,0766	1526,984	2921,674
-273,414	74754,99	54913,8
-148,784	22136,71	15532,51
-146,073	21337,19	7,352526
-142,422	20284,12	13,32423
-178,064	31706,95	1270,362
-21,1856	448,8302	24610,97
-56,3965	3180,569	1239,809
-131,957	17412,62	5709,365
-323,811	104853,4	36807,9
-166,388	27685,12	24781,77
-122,682	15050,78	1910,29
-132,145	17462,21	89,54899
-348,301	121313,8	46723,67
-80,555	6489,111	71688,04
143,844	20691,09	50354,9
-38,3544	1471,06	33196,24
199,4414	39776,86	56546,82
563,206	317201	132324,7
558,4567	311873,9	22,55623
-92,4285	8543,033	423651,6
8,944249	79,99959	10276,44
350,2045	122643,2	116458,5
-114,207	13043,27	215678,1
175,3924	30762,5	83867,9
264,622	70024,81	7961,921
-359,099	128952	389027,8
	1719170	1990106

DW = 1,1576.

По таблице приложения 4 [1] определяем значащие точки d_L и d_U для 5% уровня значимости.

Для m = 2 и n = 32: d_L = 1,28; d_U = 1,57.

Так как DW < d_L (1,1576<1,28), то нулевую гипотезу об отсутствии автокорреляции мы не можем принять. Следовательно, в модели присутствует автокорреляция остатков случайных отклонений.

Проверим наличие автокорреляции, используя тест Бреуша-Годфри. Тест основан на следующей идее: если имеется корреляция между соседними наблюдения­ми, то естественно ожидать, что в уравнении

, t = 1,…, n

(где e_t— остатки регрессии, полученные обычным методом наи­меньших квадратов), коэффициент ρ окажется значимо отли­чающимся от нуля.

Значение коэффициента ρ представлено в таблице 1.5.

Таблица 1.5.

	Столбец 1	Столбец 2
Столбец 1	1
Столбец 2	0,620823	1

Проверим значимость коэффициента корреляции, находим наблюдаемое значение по формуле:

=4,265

T>t_кр, следовательно коэффициент корреляции значим, и в модели присутствует автокорреляция остатков случайных отклонений.
Проведем графический анализ гетероскедастичность. Построим график, где по оси абсцисс будем откладывать расчетные значения Y, полученные из эмперического уравнения регрессии, а по оси ординат квадраты остатков уравнения е². График представлен на рисунке 1.1.

Рисунок 1.1.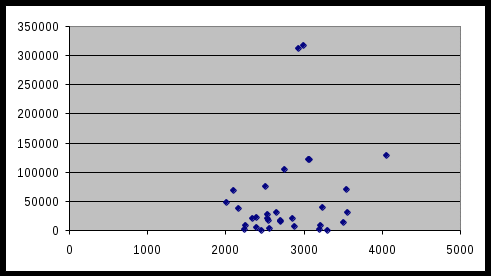


Анализируя график, можем предположить непостоянство дисперсий. Т. е. наличие гетероскедастичности в модели.

Проверим наличие гетероскедастичности, используя тест Вайта.

Строим регрессию:

ε² = a + b₁x₁ + b₁₁x₁² + b₂x₂ + b₂₂x₂²+ b₁₂∙x₁∙x₂

Результаты теста представлены в таблице 1.6.

Таблица 1.5.

	df	SS	MS	F	Значимость F
Регрессия	5	1,91E+10	3,82E+09	0,582977	0,712725
Остаток	26	1,7E+11	6,55E+09
Итого	31	1,89E+11

Результаты теста Уайта показывают отсутствие гетероскедастичности, так как при 5% уровне значимости F_факттабл. Р-вероятность принятия гипотезы о гетероскедастичности равна 0,713, что больше 0,05.

Для проверки наличия гетероскедастичности воспользуемся тестом Парка. В Excel рассчитаем логарифмы значений e², X1 и X2 (см. табл. 1.7).

Таблица 1.7.

lne2	lnX1	lnX2
10,7744	6,529565	4,51042
10,5517	6,66772	4,479494
8,409718	6,815092	4,465678
11,14585	6,658139	4,448516
9,067974	6,687483	4,50976
7,33105	6,701715	4,485936
11,22197	6,838405	4,505792
10,00499	6,767113	4,514041
9,968207	6,745001	4,504244
9,917593	6,82622	4,533244
10,36429	6,847687	4,57821
6,106645	6,726233	4,592389
8,064816	6,736374	4,641309
9,76495	6,685986	4,677584
11,56032	6,812015	4,669084
10,22865	6,658011	4,693913
9,619185	6,731137	4,717069
9,767794	6,753555	4,694737
11,70614	6,93644	4,703204
8,777881	6,81564	4,729509
9,937458	6,805723	4,725882
7,293739	6,996224	4,703023
10,59104	7,032271	4,686658
12,66729	6,92844	4,676001
12,65035	6,898715	4,676281
9,052871	7,008053	4,701752
4,382021	7,034124	4,71151
11,71703	6,924416	4,712139
9,476027	7,114037	4,718856
10,33405	7,124478	4,73145
11,1566	7,113549	4,736988
11,7672	7,281661	4,761746

Построим для каждой объясняющей переменной зависимости .

Результаты в таблицах 1.8– 1.9.

Таблица 1.8.

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	2,70392	13,26605	0,203822	0,839869
Переменная X 1	1,044038	1,936061	0,539259	0,593688

Таблица 1.9.

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	3,953056	15,22128	0,259706	0,796865
Переменная X 1	1,274538	3,285978	0,387872	0,700849

В таблицах 1.8 – 1.9 рассчитана t-статистика для каждого коэффициента .

Определяем статистическую значимость полученных коэффициентов . По таблице приложения 2 [1] находим табличное значение коэффициента Стьюдента для уровня значимости  = 0,05 и числа степеней свободы v = n – 2 = 29. t_{/2; v} = t_{0,025; 29} = 2,364.

Сравнивая рассчитанную t-статистику с табличной, получаем, что ни один коэффициент не является статистически значимым. Это говорит о отсутствии в модели гетероскедастичности.

Результаты теста Парка, подтвердили результаты теста Уайта.
Вывод:

Построенное уравнение регрессии (1.1), хотя и адекватно экспериментальным данным (имеет высокий коэффициент детерминации и значимую F-статистику, все коэффициенты регрессии статистически значимы), не может быть использовано в практических целях, так как оно имеет следующие недостатки: присутствует автокорреляция остатков случайных отклонений, имеется мультиколлинеарность.

Перечисленные недостатки могут привести к ненадежности оценок, выводы по t- и F- статистикам, определяющим значимость коэффициентов регрессии и детерминации, возможно, неверны.