вар. 58. Обобщите результаты оценивания параметров модели и результаты проверки модели на адекватность
 Скачать 281 Kb. Скачать 281 Kb.
|
|
Задание 2. Используя данные из задания 1, сформулируйте и проверьте гипотезу о наличии на исследуемом временном интервале точки разрыва (имеется сдвиг свободного члена или коэффициента наклона). В случае, если предварительный графический анализ не подтверждает наличия разрыва на временном интервале, примите, что точка разрыва находится посередине. Решение. На рисунке 2.1 представлен график зависимости величины валового внутреннего продукта от времени. Предварительный графический анализ не подтверждает наличие разрыва на рассматриваемом временном интервале, предположим, что точка разрыва находится посередине рассматриваемого интервала. Найдем зависимости валового внутреннего продукта от времени на каждом из двух интервалов времени, т. е. с 2000 года по 2003 год и с 2004 года по 2007 год. Так же найдем зависимость ВВП от времени на протяжении всего временного интервала. Y1 – показатель ВВП с 2000 года по 2003 год; Y2 – показатель ВВП с 2004 года по 2007 год; Y – показатель ВВП с 2000 года по 2007 год. Найдем зависимости уравнения регрессии: Y(t) = a + b∙t, Y1(t) = a1 + b1(t); Y2(t) = a2 + b2(t), Где t – показатель времени. Результаты моделирования в Eviews представлены в таблицах 2.1- 2.3 соответственно. Рисунок 2.1. 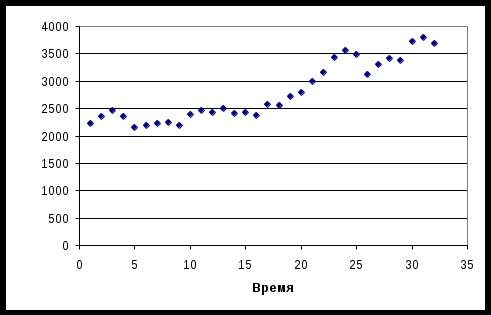 Таблица 2.1. Характеристики уравнения Y(t).
Таблица 2.2. Характеристики уравнения Y1(t).
Таблица 2.3 Характеристики уравнения Y2(t).
Проведем тест Чоу, для оценки структурной стабильности тенденции изучаемого временного ряда. Введем гипотезу Н0: тенденция изучаемого ряда структурно стабильна. Остаточная сумма квадратов по кусочно-линейной модели: Склост = С1ост + С2ост = 158432 + 483329 = 641761. Сокращение остаточной дисперсии при переходе от единого уравнения тренда к кусочно-линейной модели: ∆Сост = Сост – Склост = 1440584 – 641761 = 798823. Так как число параметров в уравнениях Y(t), Y1(t) и Y2(t) одинаково и равно k, то фактическое значение F – критерия находим по формуле: Fфакт = (798823/2)/(641761/(32 - 2∙2)) = 17,426. Критическое (табличное) значение критерия Фишера для доверительной вероятности = 0,95 и числа степеней свободы v1 = k = 2 и v2 = n - 2∙k = 32 - 2∙2 = 28: Fкр. = F0,05; 2; 28 = 3,34. Помощь на экзамене онлайн. Fфакт > Fтабл – уравнения Y1(t) и Y2(t) описывают не одну и ту же тенденцию, а различия численных оценок их параметров а1 и а2, а так же b1 и b2 соответственно статистически значимы. Следовательно, можно утверждать, что в середине рассматриваемого временного интервала ряд имеет точку разрыва. Задание 3. Введите в эконометрическую модель, построенную в задании 1 сезонные фиктивные переменные и с помощью соответствующей модели исследуйте наличие или отсутствие сезонных колебаний. Решение. Так как в уравнении (1.1) задачи 1 переменные Х1 и Х2 является статистически значимыми, то для дальнейшего анализа воспользуемся моделью, полученную нами в задании 1: Y = -1046,49 + 2,0334∙X1 + 1828,83∙X2 (3.1) (t) (-2,311) (6,181) (3,265) Значимость коэффициентов уравнения (3.1) высокая. На рисунках 3.1 и 3.3 представлены графики переменных Y, Х1 и Х2 соответственно. Рисунок 3.1.  Рисунок 3.2. 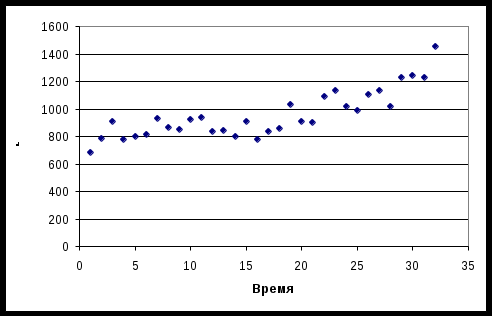 Рисунок 3.3. 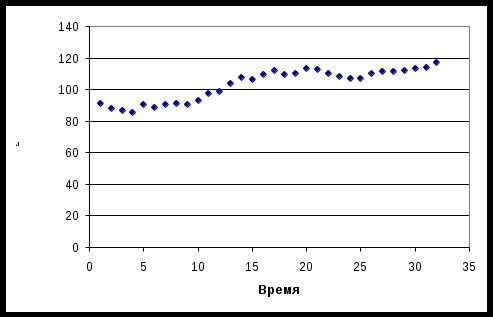 Визуальный анализ графиков переменных Y, Х1 и Х2 позволил выявить некую закономерность – повторения из года в год изменения показателей в определенные промежутки времени, т. е. сезонные колебания. Обозначим фиктивные квартальные переменные: Qit = 1, если наблюдение t относится к i-му кварталу, Qit = 0 в противном случае (i = 1, 2, 3, 4). Фиктивную переменную Q4 не будем включать в уравнение регрессии, что бы избежать «ловушки». Данные для экспорта в Eviews представлены в таблице 3.1. Таблица 3.1. Данные для экспорта в Eviews.
Уравнение регрессии будем искать в виде: Y = 0 + 1∙X1+ 2∙X2 + 1∙Q1 + d2∙Q2 + d3∙Q3 (3.2) Результаты моделирования данного уравнения в Eviews представлены в таблице 3.2. Таблица3.2
Получим следующее уравнение регрессии: Y = -966,21 + 2,1738∙X1 +16,7079∙X2 + 4,9673∙Q1 – 77,526 ∙Q2 – 134,37∙Q3 (t) (-2,025) (6,037) (2,835) (0,039) (-0,619) (-1,047) (3.3) Табличное значение критерия Стьюдента, соответствующее доверительной вероятности = 0,95 и числу степеней свободы v = n – m – 1 = 26; tкр. = t0,025;26 = 2,3788. Ни одна из квартальных переменных, входящих в уравнение (3.3) не является статистически значимой. Следовательно, можно отметить отсутствие влияния квартальных колебаний на рассматриваемые показатели. Список использованных источников. 1. Практикум по эконометрике. Под редакцией И. И. Елисеевой - М.: Финансы и статистика., 2007. - 343 с. 2. Эконометрика. Под редакцией И. И. Елисеевой - М.: Финансы и статистика., 2007. - 575 с. 3. Доугерти К. Введение в эконометрику. - М.: МГУ, 1999. - 402 с. 4. Орлов А.И. Эконометрика. – М.: Экзамен, 2002. 5. Валентинов В.А. Эконометрика. – М.: «Дашков и Ко», 2006. 6. Тихомиров Н.П., Дорохина Е.Ю. Эконометрика. – М.: Экзамен, 2003. 7. Крамер Н. Ш., Путко Б. А. Эконометрика. – М.: ЮНИТИ-ДАНА, 2005. |
