сроп. ФКХ+СРО+doc+(2). Общие рекомендации по выполнению самостоятельной работы обучающегося

• Название: Общие рекомендации по выполнению самостоятельной работы обучающегося
• Дата: 07.02.2022
• Размер: 0.82 Mb.
• Имя файла: ФКХ+СРО+doc+(2).doc
• Тип: Самостоятельная работа; #353959
• страница: 4 из 7

3.2 Зависимость теплового эффекта химической реакции от температуры
3.2.1 Рассчитать зависимость теплового эффекта химической реакции
2Cu₂S + 3O₂ = 2Cu₂O + 2SO₂
от температуры, если известен тепловой эффект реакции при 298 К

ΔН = 781,16 кДж и зависимости теплоёмкостей (Дж/(моль∙К)) участников реакции от температуры

С_Р(Cu₂S) = 39,25 + 130,54∙10^-3T

С_Р(O₂) = 31,96 + 3,99∙10^-3T – 3,57∙10⁵T^-2

С_Р(Cu₂O) = 56,57 + 29,29∙10^-3T

С_Р(SO₂) = 46,19 + 7,87∙10^-3T – 7,7∙10⁵T^-2
Решение
Зависимость теплового эффекта химической реакции от температуры

Выражается уравнением
ΔН = ΔН₀ + ∫ΔС_РdT
где ΔН₀ – постоянная интегрирования;

ΔС_Р – изменение теплоёмкости химической реакции.
Изменение теплоёмкости химической реакции определяется уравнением
ΔС_Р = 2С_Р(Cu₂O) + 2С_Р(SO₂) - 2С_Р(Cu₂S) -3С_Р(O₂)
После подстановки численных значений получим
ΔС_Р = 2(56,57 + 29,29∙10^-3T) +

2(46,19 + 7,87∙10^-3T – 7,7∙10⁵T^-2)-

2(39,25 + 130,54∙10^-3T)-

3(31,96 + 3,99∙10^-3T – 3,57∙10⁵T^-2) =

32,64 – 196,79∙10^-3T + 4,01∙10⁵T^-2
Подставив значение ΔС_Р в уравнение зависимости теплового эффекта химической реакции от температуры, получим
ΔН = ΔН₀ + ∫(32,64 – 196,79∙10^-3T + 4,01∙10⁵T^-2)dT
После интегрирования уравнения получим
ΔН = ΔН₀ + 32,64Т – 98,39∙10^-3T² - 4,01∙10⁵T^-1
На основании известного теплового эффекта химической реакции при температуре 298 К, рассчитаем постоянную интегрирования ΔН₀. Для этого в полученное уравнений подставим значение теплового эффекта и температуру 298 К, обращая внимание на соответствие размерностей теплоёмкости и теплового эффекта.
781160 = ΔН₀ + 32,64∙298 - 98,39∙10^-3∙298² - 4,01∙10⁵∙298^-1
Решая уравнение, получим
ΔН₀ = 780303 Дж
Тогда уравнение зависимости теплового эффекта химической реакции от температуры будет иметь вид
ΔН = 780303 + 32,64Т – 98,39∙10^-3T² - 4,01∙10⁵T^-1
Ответ: ΔН = 780303 + 32,64Т – 98,39∙10^-3T² - 4,01∙10⁵T^-1
3.2.2 Рассчитать зависимость теплового эффекта химической реакции
2Cu₂O + Cu₂S = 6Cu + SO₂

при температуре 1200^оС.
Решение
Зависимость теплового химической реакции от температуры

выражается уравнением
ΔН = ΔН₀ + ∫ΔС_РdT
где ΔН₀ – постоянная интегрирования;

ΔС_Р – изменение теплоёмкости химической реакции.

Для расчёта теплового эффекта химической реакции от температуры необходимо знать зависимости теплоёмкостей участников химической реакции от температуры и величину теплового эффекта этой реакции, хотя бы при одной температуре. Последнее необходимо для расчёта постоянной интегрирования ΔН₀ . Для решения задачи воспользуемся справочными данными, приведёнными в приложении А.

Для расчёта теплового эффекта реакции при температуре 298 К выпишем из приложения значения тепловых эффектов образования участников реакции при температуре 298 К.

ΔН ( Cu₂S)= -79,50 кДж/моль; ΔН ( Сu)= 0

ΔН ( Cu₂O)= -133,18 кДж/моль; ΔН ( SO₂)= -298,9 кДж/моль
Рассчитаем тепловой эффект реакции при температуре 298 К.
ΔН = ΔН ( SO₂) - ΔН ( Cu₂S) - 2 ΔН ( Cu₂O)
Подставляя численные значения, получим
ΔН = (-298,9) – (-79,50) – 2(-133,18) = 46,96 кДж
Для расчёта ΔС_Р выпишем из приложения численные зависимости теплоёмкостей (Дж/(моль∙К)) участников реакции от температуры
С_Р(Cu₂S) = 39,25 + 130,54∙10^-3T

С_Р(Сu) = 22,64 + 6,28∙10^-3T

С_Р(Cu₂O) = 56,57 + 29,29∙10^-3T

С_Р(SO₂) = 46,19 + 7,87∙10^-3T – 7,7∙10⁵T^-2
Изменение теплоёмкости химической реакции определяется уравнением
ΔС_Р = 6С_Р(Cu) + С_Р(SO₂) - С_Р(Cu₂S) -2С_Р(Cu₂O)
Подставляя численные значения, получим
ΔС_Р = 6(22,64 + 6,28∙10^-3T) +

(46,19 + 7,87∙10^-3T – 7,7∙10⁵T^-2) -

(39,25 + 130,54∙10^-3T) –

2(56,57 + 29,29∙10^-3T) =

-60,92 – 168,68∙10^-3T– 7, 7∙10⁵T^-2
Подставив значение ΔС_Р в уравнение зависимости теплового эффекта химической реакции от температуры, получим
ΔН = ΔН₀ + ∫(-60,92 – 168,68∙10^-3T– 7, 7∙10⁵T^-2)dT
После интегрирования уравнения получим
ΔН = ΔН₀ – 60,92Т – 84,34∙10^-3T² + 7,7∙10⁵T^-1
На основании известного теплового эффекта химической реакции при температуре 298 К, рассчитаем постоянную интегрирования ΔН₀. Для этого в полученное уравнений подставим значение теплового эффекта и температуру 298 К, обращая внимание соответствие размерностей теплоёмкости и теплового эффекта.

46960 = ΔН₀ – 60,92∙298 – 84,34∙10^-3∙298² + 7,7∙10⁵∙298^-1
Решая уравнение, получим
ΔН₀ = 70020 Дж
Тогда уравнение зависимости теплового эффекта химической реакции от температуры будет иметь вид
ΔН = 70020 – 60,92Т – 84,34∙10^-3T² + 7,7∙10⁵T^-1
По полученному уравнению рассчитаем тепловой эффект химической реакции при 1483^оК
ΔН = 70020 – 60,92∙1473 – 84,34∙10^-3 ∙1473² + 7,7∙10⁵ ∙1473^-1 =-202187,36 кДж
Ответ: -202187,36 кДж

3.3 Фазовые превращения
3.3.1 Зависимость давления насыщенного CdS пара (Па) от температуры гад жидким выражается уравнением
lnP = + 6,351lnT – 24,77
Определить тепловой эффект процесса испарения CdS при 900 К.
Решение
Зависимость давления насыщенного пара жидкости от температуры выражается уравнением



Откуда получим


Продифференцируем по температуре уравнение зависимости давления насыщенного пара от температуры

С учётом последнего уравнения для теплового эффекта процесса испарения жидкого CdS можно записать
ΔН = RT²∙( ) = R(3266 + 6,35T)
Подставляя в последнее уравнение численное значение температуры, получим величину теплового эффекта процесса испарения жидкого CdS при температуре 900 К.

ΔН = = 8,31(3266 + 6,35∙900) = 74632,11 Дж/моль
Ответ: 74632,11 Дж/моль


3.5.2 Зависимость константы равновесия химической реакции
MgCl₂ + H₂O = MgO + 2HCl
от температуры приведено в таблице 2.20.
Таблица 2.20 – Зависимость константы равновесия от температуры

T, K	800	810	842	866	894
КР	0,805	1,0	1,48	2,03	2,95

Вывести уравнение зависимости константы равновесия реакции от температуры и графическим способом рассчитать тепловой эффект реакции в приведённом интервале температур.
Решение

Выявим характер зависимости константы равновесия от температуры в координатах lnК_Р - . Для этого экспериментальные данные приведём к виду

Таблица 2.21 – Зависимость lnК_Р - для реакции

∙103	1,25	1,23	1,19	1,15	1,12
lnKP	-0,22	0	0,39	0,79	1,07

На основании таблицы 2.2 построим график в координатах lnK_P- .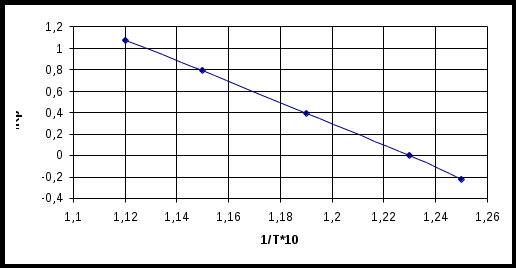



Рисунок 2.2 Зависимость lnK_P реакции от

Из графика видно, для рассматриваемой системы зависимость lnК_Р- носит линейный характер. Тогда в общем случае зависимость константы равновесия реакции от температуры можно выразить уравнением
lnК_Р = - + C
где ΔН – тепловой эффект химической реакции

В этом случае уравнение зависимости константы равновесия реакции от температуры можно получить как уравнение прямой, проходящей через две точки, лежащих на приведённой прямой.

Выпишем координаты двух точек, лежащих на прямой:

a(1/T₁ = 1,12∙10^-3; lnК_Р1=1,07); b(1/T₂ = 1,25∙10^-3; lnК_Р2= - 0,22)

Уравнение прямой, проходящeй через две точки, лежащих на этой прямой, имеет вид
(y – y₁)/(y₂ – y₁) = (x – x₁)/(x₂ – x₁)
С учётом координат построенного графика можно записать
(lnК_Р – lnК_Р1)/( lnК_Р2 – lnК_Р1) = (1/T – 1/T₁)/( 1/T₂ – 1/T₁)
Подставив численные значения координат точек, получим
(lnК_Р – 1,02)/( - 0,22 – 1,07) = (1/T – 1,12∙10^-3)/( 1,25∙10^-3 – 1,12∙10^-3)
Решая уравнение относительно lnК_Р, получим
lnК_Р = + 12,13

В нашем случае тепловой эффект химической реакции не зависит от температуры в приведённом интервале температур и определяется как тангенс угла наклона (β) прямой lnК_Р = f( ) к оси абсцисс
ΔН = R∙tgβ
Величину tgβ определим из треугольника abc, как
tgβ = = 9923
Тогда тепловой эффект процесса реакции составит
ΔН = 8,31∙9923 = 82460 Дж.
Ответ: lnК_Р = + 12,13; 82460 Дж.

3.3.3. Зависимость теплового эффекта процесса испарения четырёххлористого углерода от температуры выражается уравнением
ΔН = 45857 - 44,08Т
Определить давление насыщенного пара СCl₄ при 60^оС, если известно, что СCl₄ кипит при температуре 75^ос под давлением 101325 Па.
Решение
Зависимость давления насыщенного пара жидкости от температуры выражается уравнением


Откуда следует, что

dlnP =
Проинтегрируем полученное уравнение с учётом зависимости ΔН = f(Т) в пределах Т- Т_кип.
=

Интегрирование уравнения даёт
ln =

ln =

ln = -[5158,3( -5,37ln = 0,48
= e^0,48
= 1,62
P = 82548,3 Па
Ответ: 82548,3 Па

3.4 Равновесие в гомогенных и гетерогенных системах
3.4.1 При температуре 1093 К константа равновесия реакции
СО_газ + Н₂О_газ = СО_2(газ) + Н_2(газ)
равна 1. Рассчитать исходный состав газовой смеси, если в состоянии равновесия оказалось 20% СО₂ и 20% Н₂.
Решение
Поскольку приведённая реакция протекает без изменения числа молей газообразных участников реакции (Δn = 0), то выражение константы равновесия реакции не зависит от способа выражения концентрации участников реакции. Выразим константу равновесия через концентрацию, выраженную в процентах
К_Р =
где %i – процентное содержание i – го компонента в равновесной газовой смеси.

Для равновесного состояния справедливо
%СО₂ + %Н₂ + %СО + %Н₂О =100
С учётом содержания СО₂ и Н₂ в равновесной газовой смеси можно записать

20 + 20+ %СО + %Н₂О =100
или

%СО + %Н₂О = 60
В равновесной смеси содержится 20% СО₂ и 20% Н₂. Тогда совместное содержание СО и Н₂О в равновесной газовой фазе составит 60%. Обозначим через х процентное содержание СО в равновесной газовой смеси. Тогда содержание в ней Н₂О составит 60 – х.

Тогда константа равновесия реакции определится из уравнения
К_Р = = 1

Откуда получим

х² - 60х + 400 = 0
Решая уравнение, получим
х₁ = 52,35 и х₂ = 7,85
Тогда в равновесной газовой смеси может содержаться
52,35 %СО и 7,85 %Н₂О или
52,35 %Н₂О и 7,85 %СО
В соответствии со стехиометрией химической реакции на образование 1 моль СО₂ и 1 моль Н₂ израсходуется 1 моль СО и 1 моль Н₂О, соответственно. Это означает, что на образование 20% О₂ и 20 % Н₂ израсходуется 20% СО и 20 % Н₂О из исходной смеси соответственно.

Тогда в исходной смеси будет содержаться
52,35% + 20% = 72,35% СО и 7,65% + 20% = 27,65% Н₂О
или

7,65% + 20% = 27,65% СО иои 52,35% + 20% = 72.35% Н₂О
Ответ: 72,35% СО и 27,65% Н₂О или 27,65% СО и 72.35% Н₂О
3.4.2 Константа равновесия химической реакции
MnO_тв. + CO_газ = Mn_тв. + CO_2газ
при 700^оС равна 9,0. Определить равновесный состав газовой смеси.
Решение

Поскольку приведённая реакция протекает без изменения числа молей газообразных участников реакции (Δn = 0), то выражение константы равновесия реакции не зависит от способа выражения концентрации участников реакции. Выразим константу равновесия через концентрацию, выраженную в процентах

К_Р = = 9
Так как равновесная газовая фаза состоит только из СО и СО₂, то для её состава справедливо уравнение
%СО + %СО₂ = 100
Тогда имеем систему уравнений описывающих равновесное состояние газовой фазы

= 9
%СО + %СО₂ = 100
Решая систему уравнений, получим
%СО = 10; %СО₂ = 90
Ответ: 10 %СО и 90 % СО₂
3.4.2 Константа равновесия реакции
С_тв. + О_2газ = 2СО_газ (1)
при 1000^оС равна 1,926∙10⁵, а реакции
2СО_2газ = 2СО_газ + О_2газ (2)
при той же температуре равна 0,253∙10^-15. Рассчитать константу равновесия реакции
С_тв. + О_2газ = СО_2газ (3)
при тех же условиях.
Решение
Комбинируем реакции (1) и (2) таким образом, чтобы их сложение давало реакцию (3). Для этого реакцию (2) необходимо записать в обратном направлении

2СО_газ + О_2газ = 2СО_2газ (2^*)
Константа равновесия этой реакции (2^*) связана с константой равновесия реакции (2) уравнением


Сложение реакций (1)и (2^*) даёт реакцию (3)
С_тв. + О_2газ = 2СО_газ

2СО_газ + О_2газ = 2СО_2газ

--------------------------------

С_тв + О_2газ = 2СО_2газ
Тогда константа равновесия реакции (3) будет равна произведению констант равновесия реакций (1) и (2^*)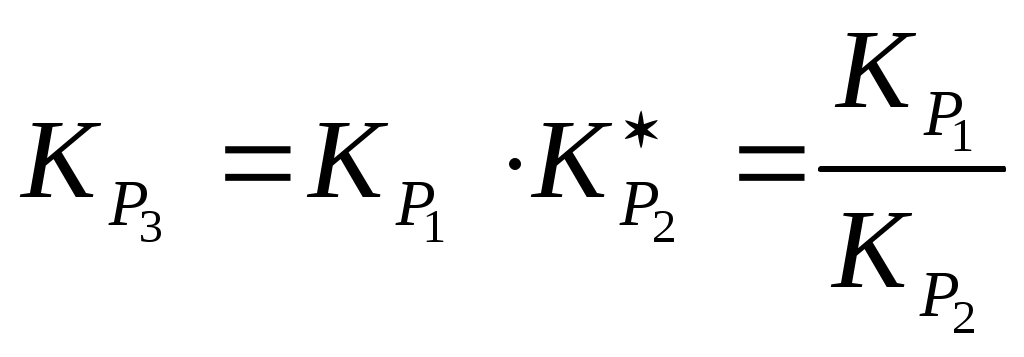

После подстановки численных значений получим
= 7,6∙10²⁰
Ответ: 7,6∙10²⁰