сроп. ФКХ+СРО+doc+(2). Общие рекомендации по выполнению самостоятельной работы обучающегося

• Название: Общие рекомендации по выполнению самостоятельной работы обучающегося
• Дата: 07.02.2022
• Размер: 0.82 Mb.
• Имя файла: ФКХ+СРО+doc+(2).doc
• Тип: Самостоятельная работа; #353959
• страница: 6 из 7

3.8 Термодинамическая теория растворов
3.8.1 Рассчитать растворимость СО₂ в воде (моль/дм³0, если парциальное давление СО₂ над раствором равно 1,013∙10⁵ па, а постоянная Генри равна 0,6∙10^-9 при концентрации СО₂, выраженной в молярных долях.
Решение
Согласно закону Генри можно записать
Х = Г ∙Р

где Х - растворимость СО₂ в воде, моль/дм³;

Г - постоянная Генри, Па^-1;

Р = давление СО₂ над раствором, Па.

Рассмотрим 1 дм³ раствора. Масса раствора из-за малой растворимости СО₂ практически составит 1000 г.Тогда в растворе будет содержаться

содержится молей воды

n 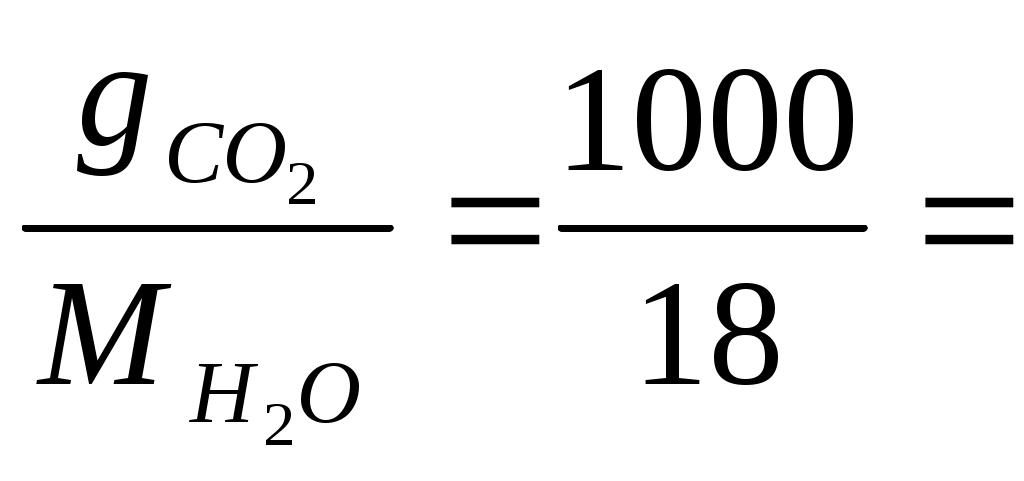= 55,56
Тогда молярная доля СО₂ в растворе составит
Х =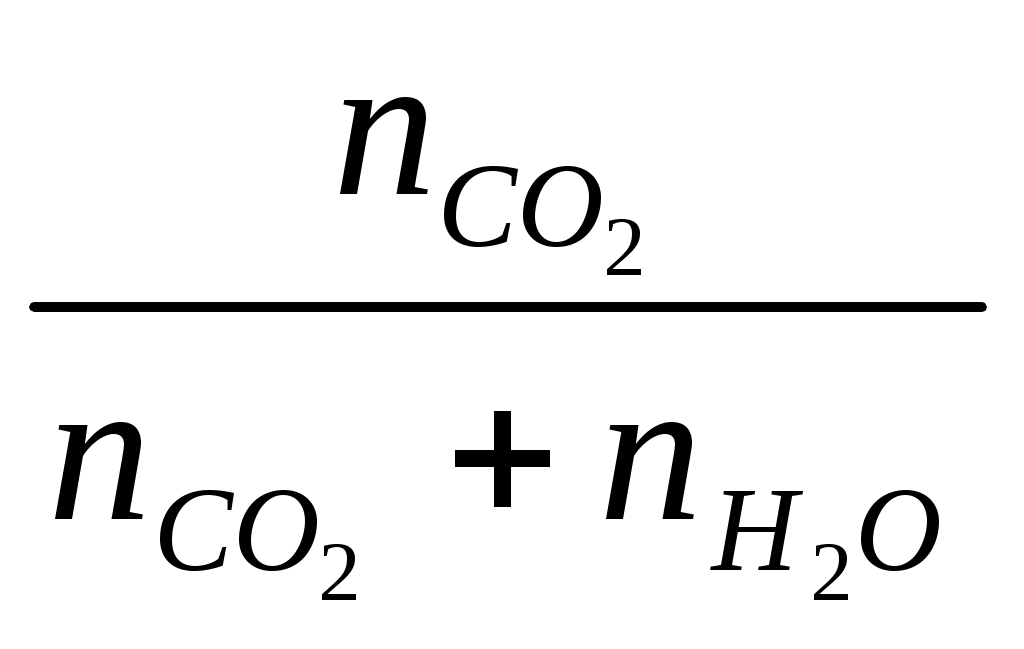
Поскольку n ›› n 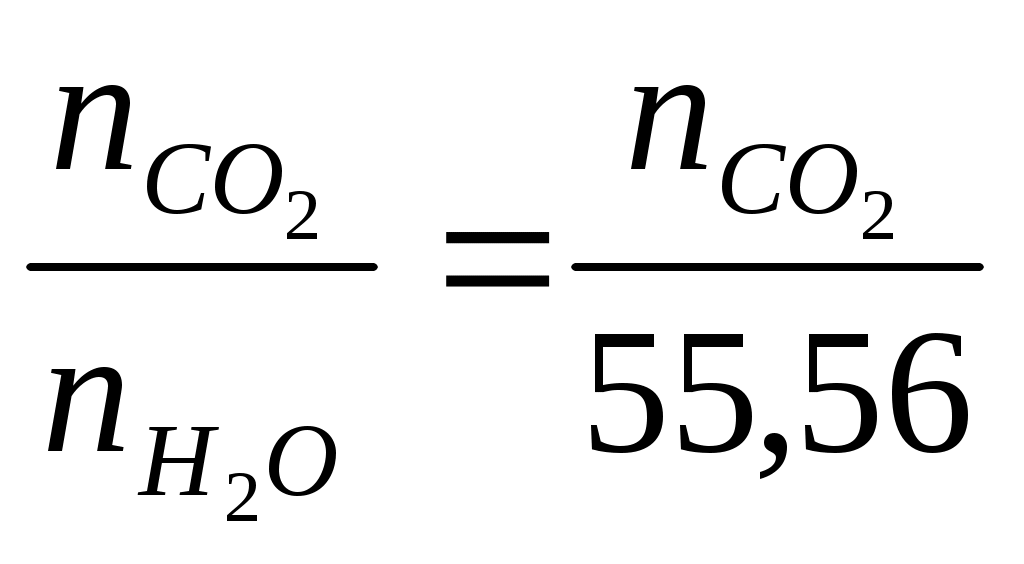то для молярной доли СО₂ справедливо
Х =
Тогда с учётом закона Генри можно записать
= 0,6∙10^-9∙1,013∙10⁵
Решая уравнение, получим
n = 3,38∙10^-3 моль
Таким образом в 1 дм³ воды содержится 3,38∙10^-3 моль СО₂. Тогда растворимость СО₂ составит 3,38∙10^-3 моль/дм³.
Ответ: 3,38∙10^-3 моль/дм³

3.8.2 Температура плавления чистого золота составляет 1275,7 К, а температура начала кристаллизации золота из расплава Au – Pb, содержащего 5,5% по массе свинца равна 1272,6 К.Определить тепловой эффект процесса плавления золота.
Решение
При растворении свинца в расславленном золоте приводит к понижению температуры, по сравнению с температуры плавления чистого золота. Понижение температуры плавления выражается уравнением
ΔТ =
где Т_о – температура плавления чистого золота (растворителя), К;

Х – концентрация растворённого свинца, мольная доля;

ΔТ – понижение температуры плавления раствора, К.

ΔН – тепловой эффект процесса плавления чистого золота, Дж/моль.

Тогда теплота плавления чистого золота определится из уравнения
ΔН =

Понижение температуры плавления раствора составит
ΔТ = Т_о – Т = 1275,7 – 1272,2 = 3,5 К
где Т – температура начала кристаллизации золота из раствора, К.

Для расчёта концентраций компонентов расплава в мольных долях рассмотрим 100 г расплава. В нём содержится 5,5 г Pb и 94,5 г Au. Тогда число молей Pb и Au в расплаве составит
n_Pb = = 0,027 моль
n_Au = = 0,478 моль
Тогда молярная доля Pb в расплаве составит
Х_{Pb =} = 0,0534
Тогда теплота плавления чистого золота составит
ΔН = = 206431 Дж
Ответ: 206431 Дж
3.8.3 Давление насыщенного пара над чистым железом при 1800 К составляет 6,13 Па. Рассчитать давление насыщенного железа при данной температуре над расплавом, приготовленным из 50 г Fe и 30 г, Mn, если образующийся раствор считать совершенным.
Решение
Поскольку каждый компонент совершенного раствора подчиняется закону Рауля, то парциапьное давление пара над раствором составит
P_Fe = X_Fe∙P
где P_Fe - парциальное давление насыщенного пара железа над раствором, Па;

P - парциальное давление насыщенного пара железа над чистым железом, Па;

X_Fe – молярная доля железа в расплаве
Рассчитаем состав раствора. Число молей железа и марганца в расплаве составит

n_Fe = 0,895
n_Mn = 0,546
g – масса металла, г;

М – молекулярный вес металла, г.
Тогда молярная доля железа в расплаве составит
Х = 0,621
Тогда парциальное давление насыщенного пара железа над раствором составит
P_Fe = 0,621∙6,13 = 3,81 Па
Ответ: 3,81 Па.
3.8.4 При 2000 К давление насыщенных паров над чистыми железом и никелем составляет соответственно 70,4 и 4520 Па. Рассчитать состав расплава, при котором общее давление пара над раствором составит 4000 Па, если раствор считать совершенным
Решение
Общее давление пара над совершенным железо - никелевым раствором составит
P = X_Fe∙P + X_Ni∙P
где P – общее давление насыщенных паров железа м никеля над раствором, Па;

P ,P - парциальное давление насыщенных паров железа и никеля над чистым железом и никелем соответственно,, Па;

X_Fe, X_Ni – молярные доли железа и никеля в расплаве соответственно.
После подстановки численных значений общего и парциальных давлений компонентов получим
4000= X_Fe∙70,4 + X_Ni∙4520
С другой стороны
X_Fе + X_Ni = 1 или X_Fе =1 - X_Ni
Тогда можно записать
4000 = (1 - X_{Ni e})∙70,4 + X_Ni∙4520
Откуда получим
X_N = 0,85; X_Fе =0,15
Ответ: 0,85; 0,15.
3.8.5 Коэффициент распределения фосфора между шлаком и металлом составляет 60, если концентрация фосфора в металле выражена в массовых процентах. Для дефосфации 200 т металла, содержащего 0,06 % по массе фосфора, использовали 10 т шлака. Рассчитать конечное содержание фосфора в металле.
Решение
Дефосфация металла осуществляется смешением фосфор содержащего металла и шлака, не содержащего фосфор. При смешении фосфор из металла переходит в шлак до установления равновесного состояния системы металл-шлак. Для установившегося равновесия коэффициент распределения фосфора между шлаком и металлом определится уравнением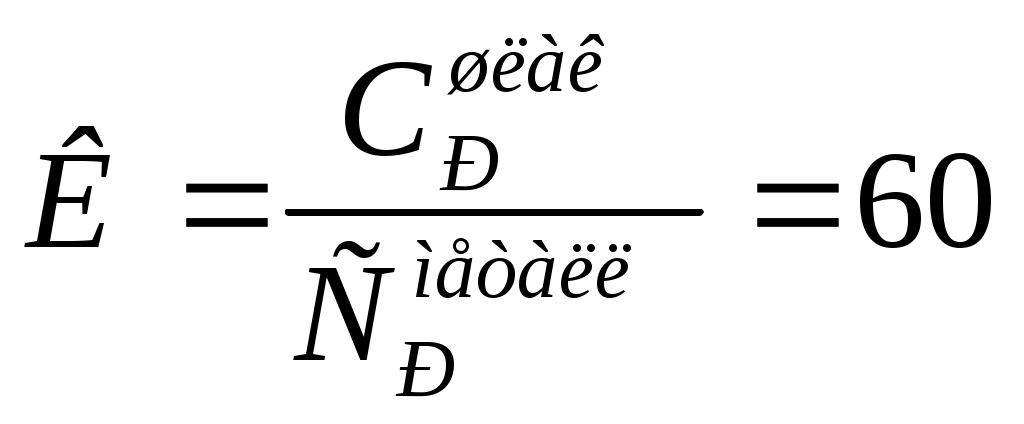

где С - концентрация фосфора в шлаке после установления равновесия в системе металл-шлак, %;

С - концентрация фосфора в металле после установления равновесия в системе металл-шлак, %;

К- константа распределения
Начальное количество фосфора в металле составляет
g = 0,12 т
Обозначим через х т массу фосфора, которая перейдет из металла в шлак в процессе дефосфации металла. Тогда в металле останется 0,12 –х т фосфора.

Тогда равновесные концентрации фосфора в шлаке и металле в массовых процентах составят
С = 10х
С =

Тогда коэффициент распределения фосфора между шлаком и металлом выразится уравнением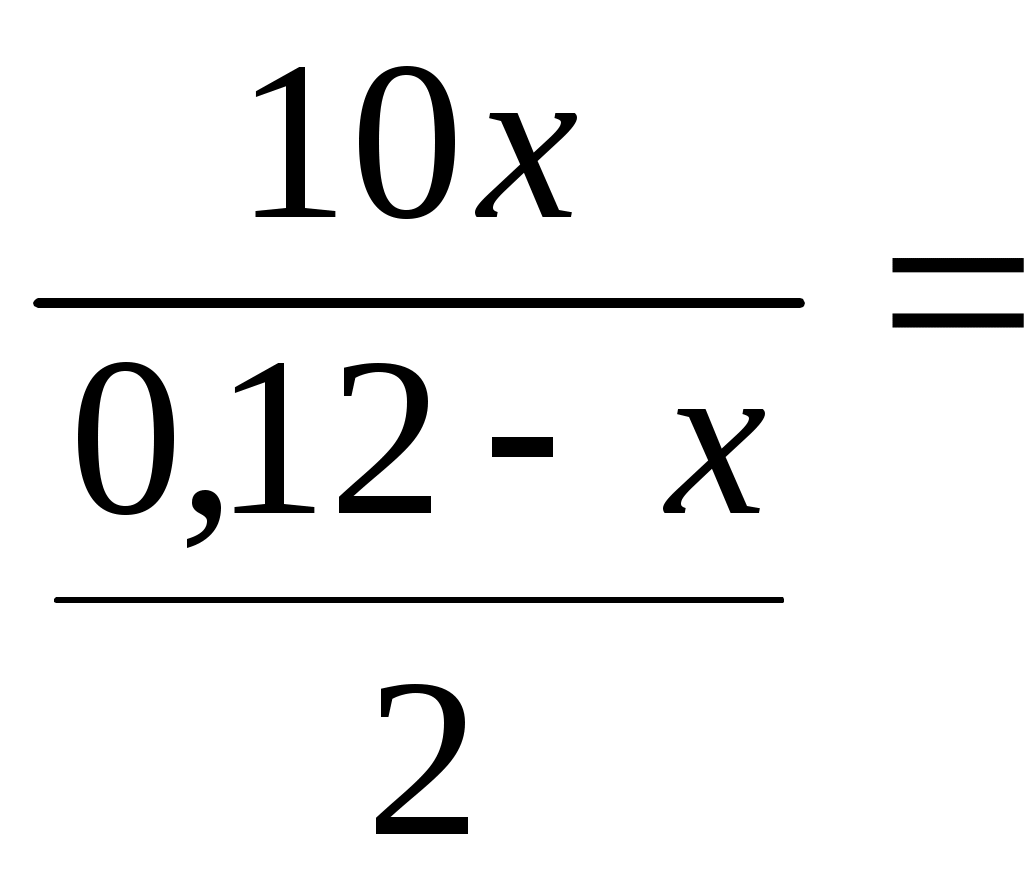
60
Решая уравнение, получим

х = 0,09 т
Тогда в металле останется фосфора
0,12 – 0,09 =0,03 т

Остаточная концентрация фосфора в металле после процесса дефосфации составит
С = 0,015 %.
Ответ: 0,015 %
3.8.6 Зависимость давления насыщенного пара магния от состава Mg - Cu

расплава при 1000 К приведена в таблице 2.22.
Таблица 2.22 – Давление насыщенного пара магния над Mg – Cu расплавом

ХMg	1,0	0,936	0,765	0,581	0,330	0.224
PMg∙10-2, Па	14,27	13,13	10,45	5,46	1,13	0,38

Определить активность и коэффициент активности магния и характер отклонения от закона Рауля, если концентрация магния выражена в молярных долях.
Решение
Для расчёта активности магния принимаем за стандартное состояние чистый магний. Тога активность магния определится уравнением

где Р_Mg – давление насыщенных паров магния над Сu – Mg расплавом, Па;

Р - давление насыщенных паров магния над чистым магнием, Па.

- активность магния в расплаве.
Коэффициент активности магния рассчитаем по уравнению


где γ – коэффициент активности;

Х_Mg – молярная доля магния в расплаве.
Результаты расчётов сведём в таблицу 2.23
Таблица 2.23 – Активность и коэффициент активности магния в Сu – Mg расплаве

XMg	1,0	0,936	0,765	0,581	0,330	0.224
	1,0	0,92	0,773	0,383	0,079	0,027
γMg	1,0	0,983	0,958	0,659	0,239	0,121

Так как коэффициент активности γ_Mg < 1, то имеет место отрицательное отклонение от закона Рауля.
3.9 Кинетика химических реакций
3.9.1 Константа скорости некоторой химической реакции первого порядка равна 2,05∙10^-3 мин^-1. Определить период полураспада химической реакции и рассчитать, сколько процентов исходного вещества прореагирует за 25 минут и за какой период времени прореагирует 90% исходного вещества.
Решение
Для реакции первого порядка период полураспада реакции определяется уравнением

t_1/2 =
где k – константа скорости химической реакции, мин^-1.

После подстановки численных значений, получим
t_1/2 = = 338 мин = 5,64 час

Кинетическое уравнение химичкой реакции первого порядка выражается равнением

kt =
где х – количество вещества, прореагировавшего за время t, %.

Рассчитаем, какое количество вещества прореагирует за 25 минут. После подстановки численных значений получим
2,05∙10^-3∙25 =ln
0,0513 = ln
e^0,0513 =
1,0523 =
х = 5.0 %
Рассчитаем период времени, за которое прореагирует 90% исходного вещества
2,05∙10^-3∙t = ln
2,05∙10^-3∙t = ln = ln10 = 2,302
t = 1123 мин = 18,71 час.
Ответ: 5,64 час; 5.0 %; 18,71 час.

3.9.2 На нагретой до 1373 К вольфрамовой проволоке аммиак разлагается по реакции
2NH₃ = N₂ +3H₂
Определить порядок реакции, если при начальном давлении аммиака 3.5∙10⁴ Па период полураспада реакции составляет 7,6 минут, а при начальном давлении аммиака 1,72∙10⁴ Па период полураспада составляет 3,7 минут.

Решение
Если известны значения периодов полураспада реакции при двух начальных концентрациях исходного вещества, то порядок реакции можно рассчитать по уравнению
n =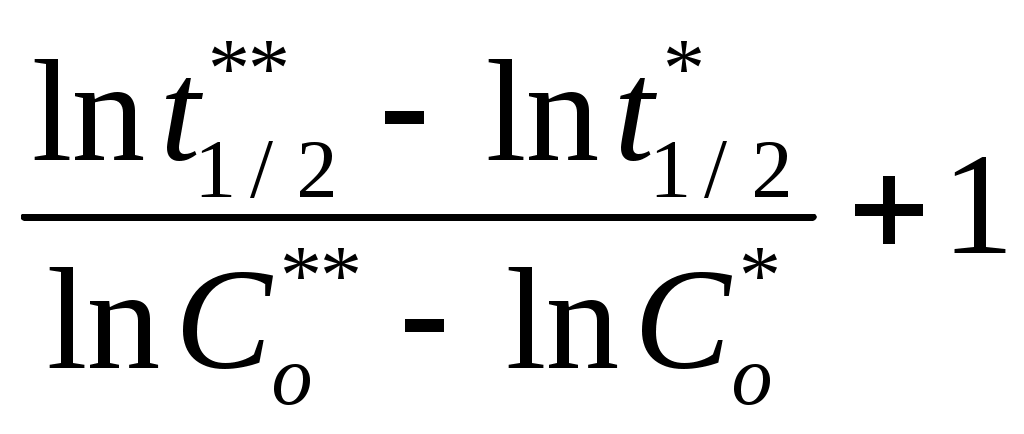
Поскольку величина давления аммиака пропорциональна его концентрации, порядок исходной реакции можно рассчитать по уравнению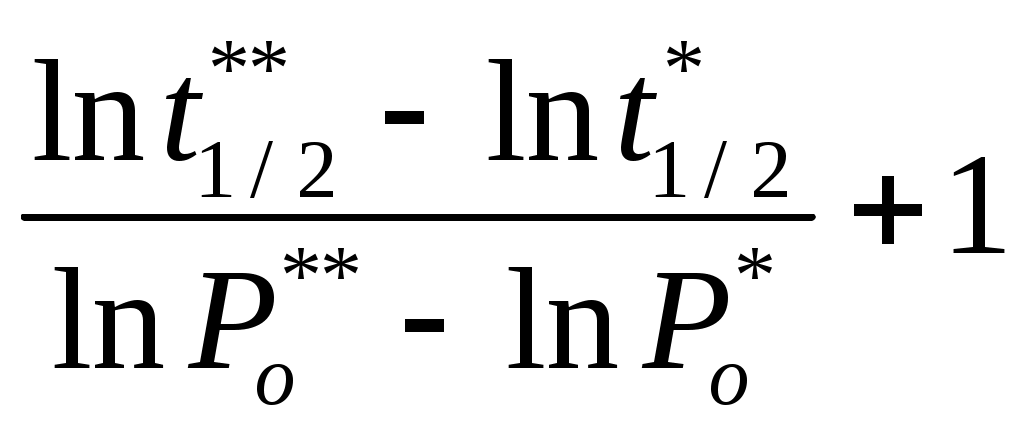




n =


После подстановки в последнее уравнение численных значений получим
n = = 2
Ответ: 2.
3.9.3 Определить энергию активации химической реакции
Cu + (NH₄)₂S₂O₈ = CuSO₄ + (NH₄)₂SO₄
если известны константы скорости данной реакции при различных температурах (Таблица 2.24)
Таблица 2.24 –Значения константы скорости реакции при различных температурах

Т,К	285,7	313,4	363,6	395,2
k∙108	9,6	18,16	39,96	61,6

Решение
Зависимость скорости химической реакции от температуры выражается уравнением
lnk =

где k – константа скорости химической реакции;

Е – энергия активации химической реакции, Дж/моль
Приведём исходные данные к виду (Tаблица 2.25)

Таблица 2.25 – Значения lnk в зависимости от 1/Т

.

	3,5	3,19	2,75	2,53
lnk	-16,16	-15,52	-14,73	-14,3

По полученным данным строим график lnk = f( )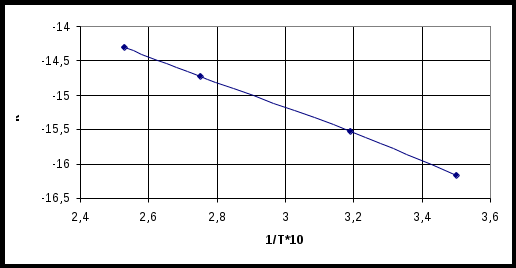



Рисунок 2.5 Зависимость lnk = f( )
Из сравнения графика с уравнением зависимости скорости химической реакции от температуры следует

Е = R∙tgβ
где β – угол наклона прямой lnk = f( ) к оси абсцисс.

Тангенс угла наклона найдём из треугольника abc, построенного через конечные точки, лежащие на искомой прямой
tgβ = = 31299
Тогда энергия активации химической реакции составит
Е = 8,31∙31299 = 260094 Дж/моль
Ответ: 260094 Дж/моль

3.9.4 Рассчитать константу скорости химической реакции и концентрацию исходных веществ через 2 часа
СO + Cl₂ = COCl₂
если известны опытные данные (Таблица 2.26)
Таблица 2.26 – Зависимость концентрации реагирующих веществ от времени

t, мин.	12	18	24	301	42
CCO = C , кмоль∙м-3	0,01794	0,01764	0,01734	0,01704	0,01644

Принять, что скорость реакции подчиняется уравнению скорости реакции второго порядка.
Решение

Кинетическое уравнение реакции второго при выражении скорости реакции через исходные вещества при условии одинаковых начальных концентраций исходных веществ имеет вид
- = kC²

После разделения переменных уравнения получим
- = kdt

Определённое интегрирование уравнения в пределах С₁ – С₂ и t₁ – t₂ соответственно даёт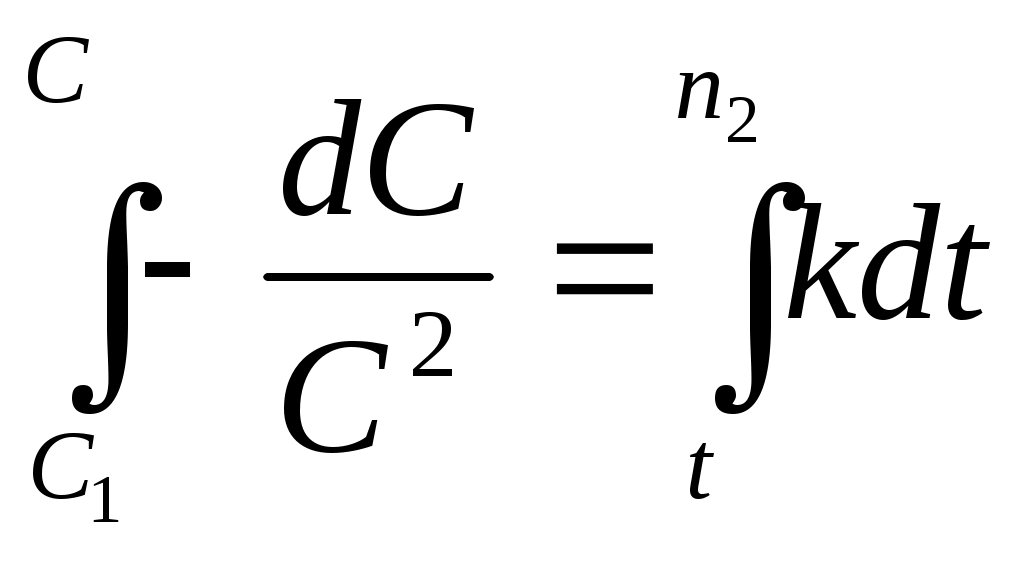


или



Откуда получим

k =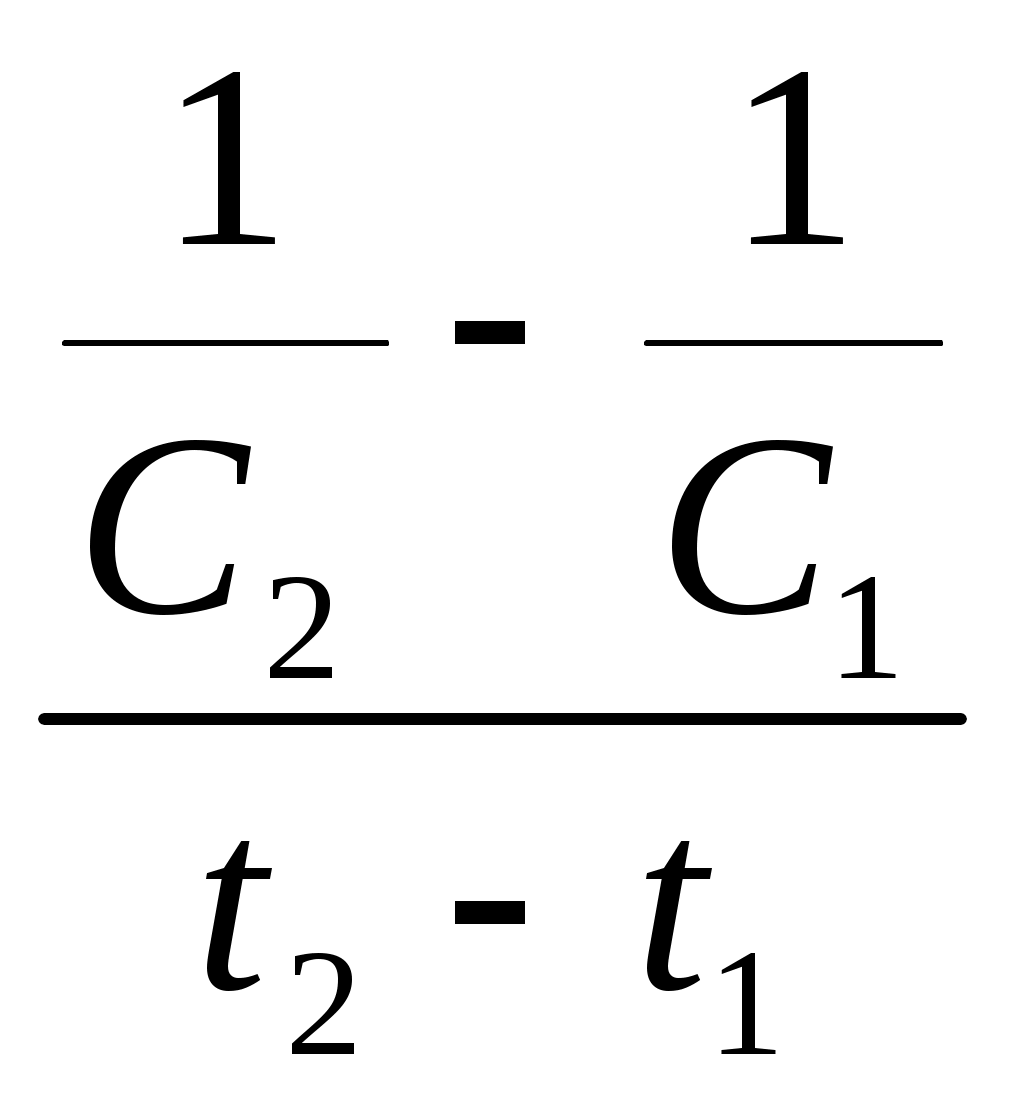

Рассчитаем несколько значений константы скорости химической реакции
k₁ = 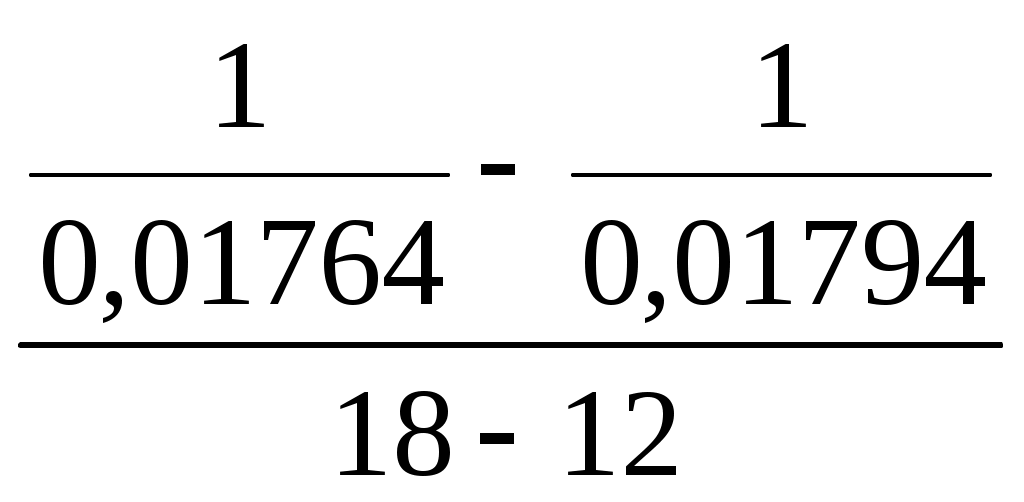= 0,158

k₂ = 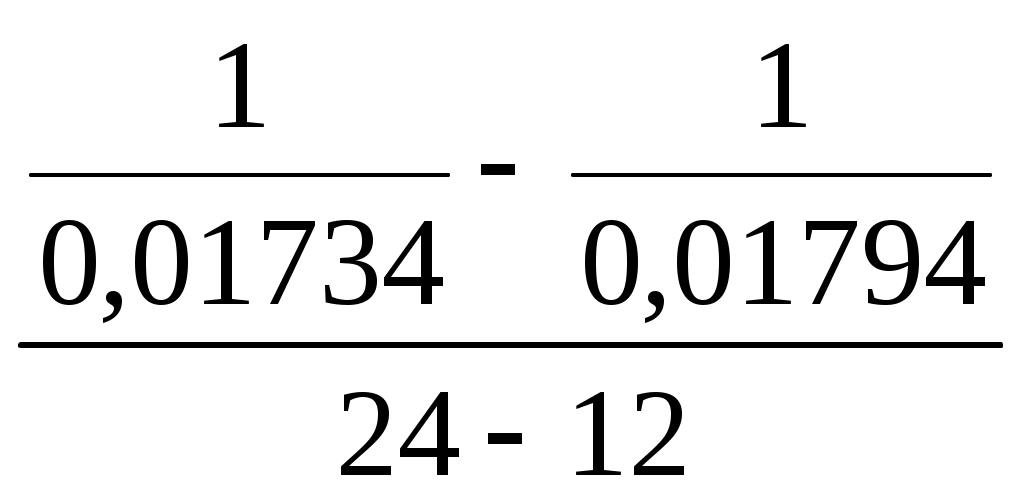= 0,160

k₃ = 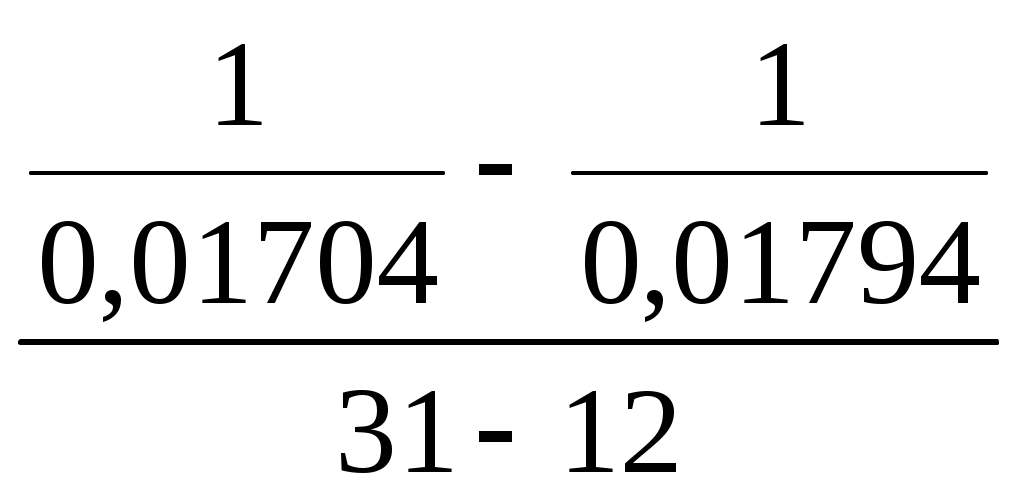= 0,155
Средняя величина константы скорости химической реакции составит
k = = 0,158 кмоль^-1∙м³∙мин^-1
Концентрацию СО = Сl₂через 2 часа, равную С₂, рассчитаем по уравнению


или


После подстановки численных значений получим
=72,8053
С₂ = 0,0137 кмоль∙м^-3

Ответ: 0,0137 кмоль∙м^-3

3.9.5 Во сколько раз надо изменить давление в системе
СO + Cl₂ = COCl₂
чтобы скорость прямой реакции увеличилась в 16 раз.
Решение
Считая, что начальные концентрации СO и Cl₂ одинаковы, для скорости этой химической реакции можно записать
w = kС²
где k - константа скорости химической реакции.

Проведём два опыта при различных начальных концентрациях исходных веществ. Тогда уравнение скоростей химической реакции составит
w₁ = kС и w₂ = kС
где С_1,о и С_2,о – начальные концентрации исходных веществ в опыте 1 и 2 соответственно.

По условию задачи имеет место соотношение между скоростями реакций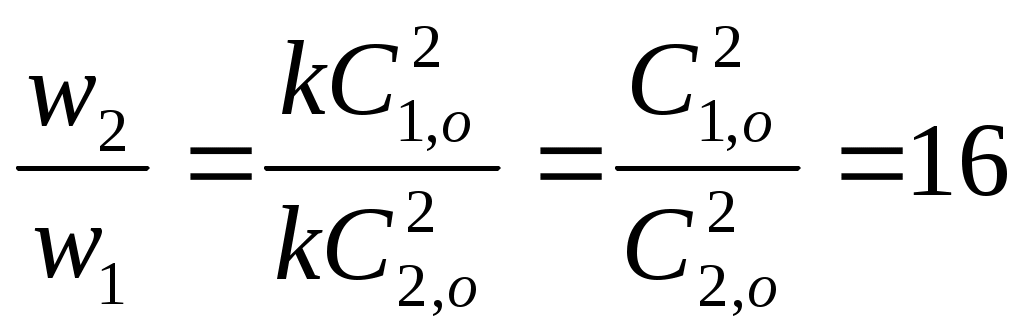


или


С другой стороны концентрация исходных веществ может быть выражена уравнением

С_i =

где С_i - концентрация реагирующего вещества, моль/дм³;

n_i – число молей i – го компонента, содержащегося в объёме V.

Тогда соотношение между скоростями реакции можно записать в виде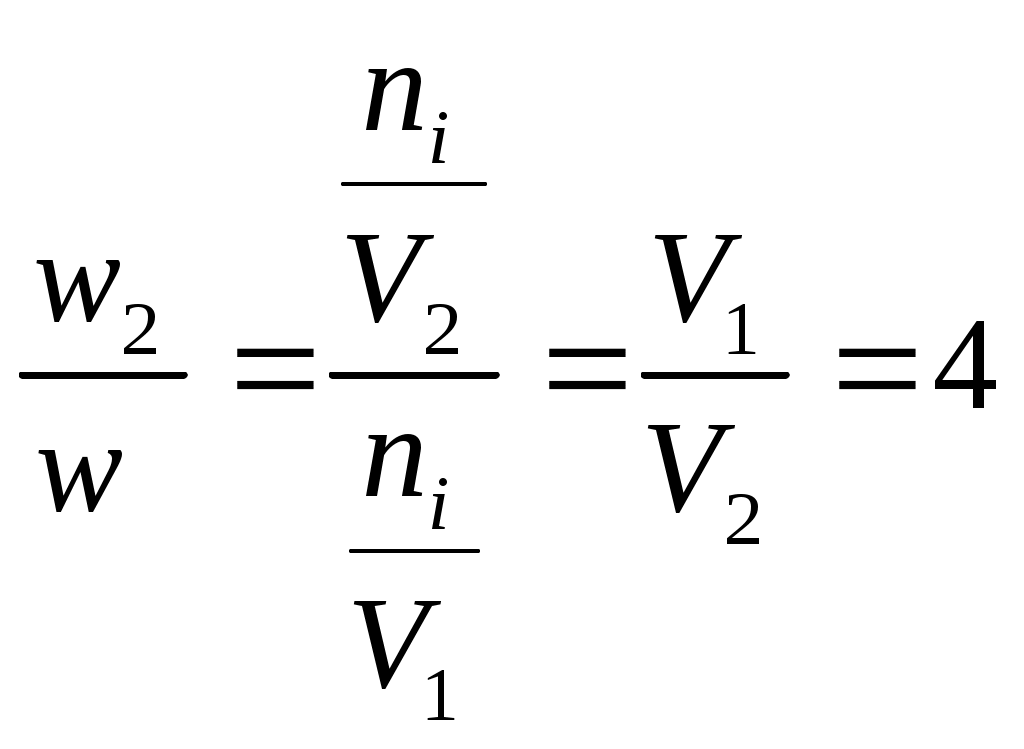

Таким образом, чтобы скорость реакции возросла в 16 раз необходимо уменьшить объём реагирующих веществ в 4 раза. Это означает, что давление в системе надо увеличить в 4 раза.
Ответ: Увеличить давление в системе в 4 раза.