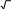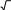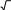Оценочные и методические материалы по математике для 59 классов

• Название: Оценочные и методические материалы по математике для 59 классов
• Дата: 14.11.2021
• Размер: 272.37 Kb.
• Имя файла: ocenochnye_i_metodicheskie_materialy_po_matematike.docx
• Тип: Документы; #271491
• страница: 7 из 8

Блок «Геометрия»

7. класс

Контрольная работа № 1.
1 вариант. Три точки В, С, иD лежат на одной прямой. Известно, что ВD = 17 см, DC = 25 см. Какой может быть длина отрезка ВС ? Сумма вертикальных углов МОЕ иDOC,образованных при пересечении прямых МС иDE,равна 2040. Найдите угол МОD . Спомощью транспортира начертите угол, равный 780, и проведите биссектрису смежного с ним угла.	2вариант. Три точки М, Nи К лежат на одной прямой. Известно, что MN = 15 см, NK = 18 см. Каким может быть расстояние МК? Сумма вертикальных углов АОВи СОD,образованных при пересечении прямых АDиВС,равна 108 0. Найдите угол ВОD. Спомощью транспортира начертите угол, равный 1320, и проведите биссектрису одного из смежных с ним углов.
Контрольная работа № 2.
1 вариант. На рисунке 1отрезки АВиСDимеют общую середину О.Докажите, что DAO CBO. С АO В D Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что  АDВ = АDС. Докажите, что АВ =АС . В равнобедренном треугольнике с периметром 48 см боковая сторона относится к основанию как 5: 2. Найдите стороны треугольника.	2 вариант. На рисунке 1отрезки МЕи РК точкойDделятся пополам. Докажите, что  КМD = РЕD. М К D Р Е На сторонах угла Dотмечены точки МиК так, что DМ=DК.Точка Р лежит внутри угла Dи РК =РМ.Докажите, что луч DР–биссектриса угла МDК. В равнобедренном треугольнике с периметром 56 см основание относится к боковой стороне как 2: 3. Найдите стороны треугольника.

Контрольная работа № 3.
1 вариант. Отрезки EFи PQпересекаются в их середине М.Докажите, что РЕ//QF. Отрезок DM– биссектриса треугольника CDE. Через точку М проведена прямая, параллельная стороне CDи пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если CDE 680 . На рисунке АС // ВD, точка М – середина отрезка АВ. Докажите, что М – середина отрезка CD. D M A B C	2 вариант. Отрезки МNи ЕFпересекаются в их середине Р.Докажите, что ЕN//МF. Отрезок AD– биссектриса треугольника АВС. Через точку Dпроведена прямая, параллельная стороне FDи пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАC 720. 3). На рисунке AB // DC, АВ = DC. Докажите, что точка О– середина отрезков АСиВD. В С О А D

Контрольная работа № 4.
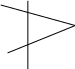
1вариант. На рисунке: АВЕ1040, DCF760, АС12 см. Найдите сторону АВтреугольника АВС. Е BМ АCD F В треугольнике СDEточка Млежит на стороне СЕ, причём СМD- острый. Докажите, что DE>DM. Периметр равнобедренного тупоугольного треугольника равен 45см, а одна из его сторон больше другой на9 см. Найдите стороны треугольника.	2 вариант. 1). На рисунке: ВАЕ1120, DBF680, ВС9 см. Найдите сторону АСтреугольника АВС. ЕМ A С В DF В треугольнике MNP точка К лежит на стороне MN, причём NKP- острый. Докажите , что КР< МР. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.
Контрольная работа № 5.
1вариант. В остроугольном треугольнике МNPбиссектриса угла М пересекает высоту NK в точке О, причём ОК = 9 см. Найдите расстояние от точки Одо прямой МN. Постройте прямоугольный треугольник по гипотенузе и острому углу.	2 вариант. В прямоугольном треугольнике DCEс прямым углом С проведена биссектриса EF, причём FC=13см. Найдите расстояние от точки Fдо прямой DE. Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.

3). Один из углов прямоугольного треугольника равен 600, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу .	3). В треугольнике АВС В 1100 , биссектрисы углов Аи Спересекаются в точке О. Найдите угол АОС.
Итоговая контрольная работа
1вариант. В равнобедренном треугольнике АВСс основанием АС угол В равен 42 0. Найдите два других угла треугольника АВС. Величины смежных углов пропорциональны числам 5 и 7. Найдите разность между этими углами. В прямоугольном треугольнике АВСС900 , А300 ,АС=10см,СD АВ,DE АС. Найдите АЕ. В треугольнике МРКугол Р составляет 600углаК, а угол М на 40больше угла Р. Найдите угол Р.	2 вариант. В равнобедренном треугольнике АВСс основанием АС сумма углов А и Сравна 1560. Найдите углы треугольника АВС. Величины смежных углов пропорциональны числам 4и 11. Найдите разность между этими углами. В прямоугольном треугольнике АВСС900 , В 300 ,ВС=18см,СК АВ,КМ ВС. Найдите МВ. В треугольнике BDE угол Всоставляет 30 0угла D, а угол Е на 19 0больше угла D. Найдите угол В.

7. 
   класс
   

Контрольная работа № 1.
1 вариант. Диагонали прямоугольника ABCDпересекается в точке О, ABO= 36°. Найдите  AOD. Найдите углы прямоугольной трапеции, если один из ее углов равен 20°. Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма. В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции. * Высота ВМ, проведенная из вершины угла ромба ABCDобразует со стороной АВугол 30°,АМ = 4 см. Найдите длину диагонали BDромба, если точка Млежит на стороне AD.	2 вариант. 1). Диагонали прямоугольника MNKPпересекаютсяв точке О,  MON= 64°. Найдите  ОМР. 2). Найдите углы равнобокой трапеции, если один из ее углов на 30° больше второго. Стороны параллелограмма относятся как 3:1, а его периметр равен 40см. Найдите стороны параллелограмма. В прямоугольной трапеции разность углов при одной из боковых сторон равна 48°. Найдите углы трапеции. * Высота ВМ,проведенная из вершины угла ромба ABCDобразует со стороной АВугол 30°,длина диагонали АС равна 6 см. Найдите AM,если точка М лежит на продолжении стороны AD.
Контрольная работа № 2.

1 вариант. Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника. Катеты прямоугольноготреугольника равны 6и 8см. Найдите гипотенузу и площадь треугольника. 3). Найдите площадь и периметр ромба, если его диагонали равны 8 и 10см. 4).* В прямоугольной трапеции АВСКбольшая боковая сторона равна 32 см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции.	2 вариант. Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника. Один из катетов прямоугольного треугольника равен 12см, а гипотенуза 13см. Найдите второй катет и гипотенузу треугольника. Диагонали ромба равны 10 и 12см. Найдите его площадь и периметр. * В прямоугольной трапеции ABCDбольшая боковая сторона равна 8см, угол А равен 60°, а высота ВНделит основание ADпополам. Найдите площадь трапеции.
Контрольная работа № 3.
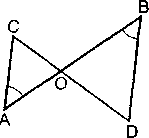
1 вариант. 1). По рис. A= B, СО=4, DO=6, АО=5. Найти:а). ОВ; б). АС:BD;в). SAOC: SBOD. В треугольнике ABC сторона АВ = 4 см, ВС =7см, АС=6см, а в треугольнике MNKсторона МК =8см,MN=12см,KN=14см. Найдите углы треугольника MNK,если  A= 80°,  B= 60°. Прямая пересекает стороны треугольника ABCв точках Ми Ксоответственно так, что МК|| АС,ВМ: АМ= 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника ABCравен25см. 4). В трапеции ABCD(ADи ВС основания) диагонали пересекаются в точке О,AD=12см,ВС =4см.Найдите площадь треугольника ВОС,если площадь треугольника AODравна 45см2.	2 вариант. 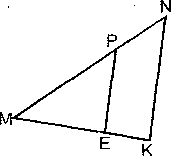1). По рис.РЕ||NK,MP=8,MN= 12,ME= 6.Найти:а) .МК; б). РЕ:NК; в). SMEP: SMKN. 2). В ∆АВСАВ = 12 см, ВС = 18 см,  В = 70 0, а в ∆МNКМN=6см,NК =9см, N=700. Найдите сторону АСи угол Стреугольника АВС, если МК=7см, К=600. Отрезки АВи CDпересекаются в точке О так, что  ACO= BDO,АО:ОВ=2:3. Найдите периметр треугольника АСО,если периметр треугольника BODравен 21см. В трапеции ABCD( ADи ВС основания) диагонали пересекаются в точке О,SAOD=32см2, SBOC= 8см2. Найдите меньшее основание трапеции, если большее из них равно 10см.

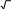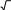
Контрольная работа № 4.

1 вариант. Средние линии треугольника относятся как 2 : 2 : 4, а периметр треугольника равен 45 см. Найдите стороны треугольника. Медианы треугольника ABCпересекаются в точке О.Через точку Опроведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС в точкахЕ и Fсоответственно. Найдите EF,если сторона АСравна 15 см. В прямоугольном треугольнике ABC( C=90°)АС=5см, ВС =5 3 см. Найдите угол Ви

2 вариант. Стороны треугольника относятся как 4 : 5 : 6, а периметр треугольника, образованного его средними линиями, равен 30 см. Найдите средние линии треугольника. Медианы треугольника MNKпересекаются в точкеО. Через точку Опроведена прямая, параллельная стороне МК и пересекающая стороны MNи NKв точках А и В соответственно. Найдите МК, если длина отрезка АВравна 12 см. 3). В прямоугольном треугольникеРКТ( T= 90°), РТ = 7 3 см, КТ= 1см. Найдите угол Ки гипотенузу КР.

гипотенузу АВ. В треугольнике ABC A= , C= , сторона ВС=7 см,ВН–высота. Найдите АН. В трапеции ABCDпродолжения боковых сторон пересекаются в точке К, причем точка В —середина отрезка АК. Найдите сумму оснований трапеции, если AD=12 см.	В треугольнике ABC A= , C= ,высота ВНравна 4 см. Найдите АС. В трапеции MNKPпродолжения боковых сторон пересекаются в точке Е, причем ЕК = КР.Найдите разность оснований трапеции, если NK =7см.
Контрольная работа № 5.
1 вариант. АВ и АС - отрезки касательных, проведенных к окружностирадиуса 9 см. Найдите длины отрезков АСи АО, если АВ= 12 см. По рисунку  АВ: BC=11:12.Найти: BCA, BAC. Хорды MNи РК пересека- ются в точке Етак, что ME=12см, NE=3 см, РЕ=КЕ.Найдите РК. Окружность с центром Ои радиусом16 см описана около треугольника ABCтак, что угол OABравен 30°,угол OCBравен 45°.Найдите стороны АВи ВСтреугольника.	2 вариант. MNи МК - отрезки касательных, проведенных к окружности радиуса 5 см. Найдите MNи МК,если МО= 13см. По рисунку  AB: АС=5:3. Найти: BOC, ABC. Хорды АВи CDпересека – ются в точке Fтак, что AF= 4см, ВF= 16см, CF=DF. Окружность с центром Ои радиусом12смописана около треугольникаMNKтак, что угол MONравен 120°, угол NOKравен 90°. Найдите стороны MNиNKтре- угольника.