;
1 3
á)
1 3
24 .
46
  Решите уравнение: 2õ 7 5. Решите уравнение: 2õ 7 5.
2 4
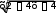  Упростите выражение: õ2 ó2 : õ1 ó1 2õ ó1 . Упростите выражение: õ2 ó2 : õ1 ó1 2õ ó1 .
Упростите выражение:
õ2 6õ 9,
åñëè
1 x1.
Контрольная работа №8 Неравенства

Контрольная работа №9
Итоговая контрольная работа

9 класс
Контрольная работа №1
Решите неравенство: а) – 5 < 2𝑥 + 1 < 3
б) (𝑥 − 3)(𝑥 + 4)(2𝑥 + 4) < 0

Найдите область определения выражения
√(𝑥2 − 13𝑥 − 42)−1
3. Даны множества А=(-∞;-3] B=[-4;5).НайдитеАUВ, А∩В.
Решитесистемунеравенств:
4 − 3𝑥

{
> 2
2
𝑥2 − 64 ≥ 0
При каких значения параметра pнеравенство
(𝑝 − 2)𝑥2 + (5𝑝 − 7)𝑥 + 𝑝 + 4 > 0
верно при всех значениях х.
Решите неравенство f(2+x)<0, если известно, что
(𝑥2 + 6𝑥 + 8)3
 𝑓(𝑥) = 𝑓(𝑥) =
6𝑥 + √24 + √42
Контрольная работа №2
Решите неравенство:

1.|3𝑥 + 8| > 2𝑥 − 13
2. а)√4𝑥 + 2 < 1 + 2𝑥
 б)√5𝑥 − 2 > 𝑥 + 2 б)√5𝑥 − 2 > 𝑥 + 2
Решите неравенство:
𝑥4 − 13𝑥2 ≥ −24 − |2𝑥3 − 14𝑥|
 При каких значениях параметра а неравенство 𝑥+3𝑎 < 0 При каких значениях параметра а неравенство 𝑥+3𝑎 < 0
𝑥+2𝑎+5
выполняется для всех xϵ[-2;-1]
Контрольная работа №3.
1. Решите графически систему уравнений
(𝑥 + 4)2 − 𝑦 = 0
Решите систему уравнений: 2.{ 𝑥𝑦 = −2
𝑥 − 4𝑦 = 6
{ 𝑦 = 𝑥 + 6
3. {
4.
(𝑥 + 1)2 − 8(𝑥𝑦 + 1) + 12 = 0
𝑦 − 𝑥 = 8
𝑥2 + 2𝑥𝑦 + 𝑦2 + 2𝑥 + 2𝑦 − 35 = 0
{ 𝑥 2 − 2𝑥𝑦 + 𝑦 2 − 2𝑦 + 2𝑥 − 3 = 0
Постройте график уравнения:
(𝑥 2 + 𝑦 2 − 10𝑥 )(𝑦 + 𝑥 − 3 ) = 0
Постройте на координатной плоскости множество точек удовлетворяющее неравенству:
𝑥 + 3𝑦 − 6  ≥ 0 −𝑥 + 𝑦 + 1
Найдите целочисленные решения системы неравенств:
 2  ﻟ ﻟ √ 𝑥 + 2𝑦 − 3 > 3 + √5 ❪ 2 ≤ ❪ 2 ≤ 1 𝗅4𝑥2 − 4𝑥𝑦 + 𝑦2 + 4 2 Контрольная работа №4.
Через две трубы, открытые одновременно, бассейн наполняется за 1 час. Если открыта только первая труба, то бассейн наполняется на 4 часа быстрее, чем, если будет открыта только вторая труба. За сколько часов можно наполнить бассейн, если открыта только вторая труба?
В двузначном положительном числе сумма квадратов цифр в 2,5 раза больше суммы его цифр и на единицу больше утроенного произведение этих цифр. Найдите наименьшее значение этого числа.


Решите систему уравнений:
{ √ 2𝑥 + 𝑦 − 6 = √ 𝑥 + 3𝑦 − 3𝑥 2 − 3𝑥𝑦 + 4𝑦 2 − 6𝑥 + 2𝑦 = 0
Решите систему уравнений:
14𝑥 2 − 16 = 𝑦(5𝑥 − 3𝑦) { 𝑥 (6𝑥 − 𝑦 ) = 8 − 𝑦 2
При каких значений параметра a система
{ |𝑥 − 2| + 2𝑦 = 6, не имеет решений? 𝑎𝑥 − 𝑦 = 1 
Контрольная работа №5.
Найдите область определения функции 𝑦 = √(3𝑥 + 7)(2𝑥 − 5)
Исследуйте функцию 𝑦 = 3𝑥5 − 2𝑥2 + 1 на четность.

Найдите наименьшее значение функции 𝑦 = 3 + 7√𝑥2 + 81 и определите, при каких значениях х оно достигается.
Постройте и прочитайте график функции:
4
 , если 2 < 𝑥 ≤ 8 , если 2 < 𝑥 ≤ 8
𝑥
2 − 2𝑥2, если − 2 ≤ 𝑥 ≤ 2
4

𝗅
− , если − 8 ≤ 𝑥 < −2
𝑥
 Исследуйте на монотонность функцию 𝑦 = 𝑥−7 Исследуйте на монотонность функцию 𝑦 = 𝑥−7
4−𝑥
а) На открытом луче (-∞;4) б) На открытом луче(4;+∞)
Постройте график этой функции.
Контрольная работа №6.
Постройте график функции 𝑦 = 2𝑥3 − 2. По графику найдите: а) Значение функции при значении аргумента, равном -3
б) Значение аргумента, если значение функции равно -1 в) Решение неравенства y>0
Решите графически уравнение:
8𝑥−2 = 5𝑥 − 3
   Упростите выражения: а) (3√10 + 3√20)(3√100) Упростите выражения: а) (3√10 + 3√20)(3√100)

б) √ √
 3 3 3 3
7 − √22 7 + √22
 Дана функция y=f(x), где 𝑓(𝑥) = 3√𝑥. Решите уравнение Дана функция y=f(x), где 𝑓(𝑥) = 3√𝑥. Решите уравнение
𝑓(𝑥2) − 5𝑓(𝑥) + 6 = 0
Последовательность (𝑎𝑛) задана рекуррентно:
𝑎1 = 6, 𝑎𝑛+1 = 𝑎𝑛 + 5
Задайте эту последовательность аналитически и найдите 𝑎98
Решите графически систему неравенств:
𝑦 − 2𝑥 < 0
 {𝑦 − 1 > 3√𝑥 {𝑦 − 1 > 3√𝑥
Дана последовательность 𝑦𝑛 = 4𝑛2 − 8𝑛 − 3
а) Докажите, что эта последовательность ограничена снизу. б) Найдите наименьший член последовательности.
в) Сколько в этой последовательности отрицательных членов?
Контрольная работа №7.
Найдите тридцатый член арифметической прогрессии -31;-28;-25…
Найдите сумму первых шести членов геометрической прогрессии 3;12;48…
Является ли число 896 членом геометрической прогрессии 𝑏𝑛 = −7 × 2𝑛
Разность шестого и восьмого члена арифметической прогрессии равна 6, а произведение четвертого и первого члена равно -8. Найдите разность и первый член данной прогрессии.
Найдите все значения х, при которых значения выражений
−7𝑥2 − 4𝑥; 𝑥 − 2; 6𝑥2 + 3𝑥
являются тремя последовательными членами арифметической прогрессии.
Первый, второй и шестой члены арифметической прогрессии представляют собой первые три члена геометрической прогрессии. Если к членам этой геометрической последовательности прибавить два, пять и 21 то получатся первые три члена некоторой геометрической прогрессии. Найдите сумму первых 90 членов исходной арифметической прогрессии.
Докажите, что для любого натурального значения n выполняется равенство:
1 · 2 + 2 · 5 + 3 · 8 + ⋯ + 𝑛(3𝑛 − 1) = 𝑛2(𝑛 + 1)
  Контрольная работа №8 Контрольная работа №8
Сколько двузначных чисел можно составить из цифр 0,1,4,7,8,9? Сколько из них нечетные?
Вычислите:

23!
20! 5!
Сколькими способами можно обозначить вершины шестиугольника буквами
A,B,C,D,E,F.
Случайным образом выбрали двузначное число. Какова вероятность того, что остаток от его деления на 7 будет равен 6.
Случайным образом выбирают решение неравенства |x+5|<10. Какова вероятность того, что оно окажется и решением неравенства 𝑥2 − 64 ≤ 0
На пробном экзамене по математике учащиеся получили следующие баллы по 100 бальной шкале: 49,45,46,60,58,49,47,48,49,60,50,49,45,46,58,47,60,49,52,51,50,49.
а) Постройте график распределения данных и распределения частот. б) Найдите размах, моду и среднее значение.
|
 Скачать 272.37 Kb.
Скачать 272.37 Kb.
 Решите уравнение: 2õ 7 5.
Решите уравнение: 2õ 7 5.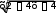
 Упростите выражение: õ2 ó2 : õ1 ó1 2õ ó1 .
Упростите выражение: õ2 ó2 : õ1 ó1 2õ ó1 .



 𝑓(𝑥) =
𝑓(𝑥) = 
 б)√5𝑥 − 2 > 𝑥 + 2
б)√5𝑥 − 2 > 𝑥 + 2 При каких значениях параметра а неравенство 𝑥+3𝑎 < 0
При каких значениях параметра а неравенство 𝑥+3𝑎 < 0 ≥ 0
≥ 0 2
2 ﻟ √𝑥 + 2𝑦 − 3 > 3 + √5
ﻟ √𝑥 + 2𝑦 − 3 > 3 + √5 ❪ 2 ≤ 1
❪ 2 ≤ 1











