Приложение 1_Эконометрика. Оценочные материалы текущего контроля успеваемости. Методические материалы по проведению процедур оценивания
 Скачать 4.57 Mb.
|
|
Рисунок 7. Фрагмент трехфакторного регрессионного анализа  .Так как  , то уравнение трехфакторной регрессии статистически значимо на 95% уровне значимости. Таким образом, связь ЧП с включенными в модель факторами существенна.Проверка предпосылки МНК о гомоскедастичности остатков При проверке предпосылки МНК о гомоскедастичности остатков в модели множественной регрессии следует вначале определить, по отношению к какому из факторов дисперсия остатков более всего нарушена. Это можно сделать в результате визуального исследования графиков остатков, построенных по каждому из факторов, включенных в модель. Та из объясняющих переменных, от которой больше зависит дисперсия случайных возмущений, и будет упорядочена по возрастанию фактических значений при проверке теста Голдфельда-Квандта. Для трехфакторной модели нашего примера графики остатков относительно каждого из трех факторов имеют вид, представленный на рисунке (эти графики легко получить в отчете, который формируется в результате использования инструмента Регрессия в пакете Анализ данных). 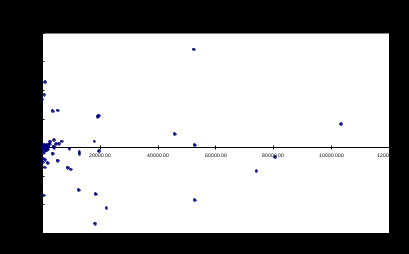 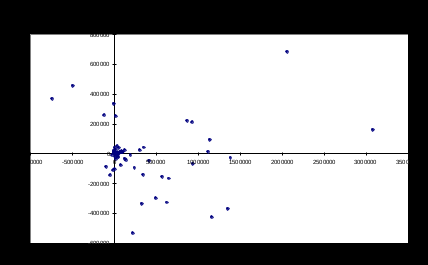 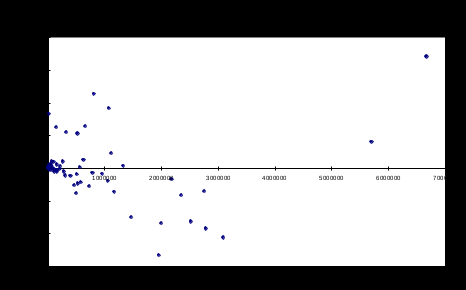 Рисунок 8. Графики остатков по каждому из факторов трехфакторной модели На каждой из диаграмм ярко выражена направленность в распределении остатков, то есть непостоянство их дисперсии. В таком случае предпосылку о гомоскедастичности остатков следует проверять трижды, каждый раз упорядочивая значения переменных по возрастанию одного из факторов. Начнем с фактора, который имеет самое большое значение t-статистики, то есть с фактора ПП (t=10,282). Основные этапы теста Голдфельда-Квандта: 1. Упорядочим переменные Y – ЧП,  – ОС,  – КО по возрастанию фактора  – ПП (в Excel для этого можно использовать команду Данные – Сортировка – По возрастанию ).2. Уберем из середины упорядоченной совокупности С=1/4*n=1/4*109  27 значений. В результате получим две совокупности по ½*(109-27)=41 значению соответственно с малыми и большими значениями .3. Для каждой совокупности в отдельности выполним регрессионный анализ (рисунок 9). Для первой совокупности:
Для второй совокупности:
Рисунок 9. Фрагменты регрессионного анализа для первой и второй совокупностей соответственно 4. Найдем отношение полученных остаточных сумм квадратов (в числителе должна быть большая сумма):
5. Вывод о наличии гомоскедастичности остатков делаем с помощью F-критерия Фишера с уровнем значимости  и двумя одинаковыми степенями свободы  (здесь р – число параметров (коэффициентов) в уравнении регрессии): .Так как  , то обнаруживается наличие гетероскедастичности в остатках модели по отношению к фактору .Аналогично обнаруживается наличие гетероскедастичности в остатках при упорядочении значений переменных по каждому из двух оставшихся факторов и . Эти процедуры проводятся в полном соответствии с рассмотренной процедурой. Мы их опускаем.3) Оценка уровня точности модели Уровень точности модели характеризует степень отклонения в среднем фактических значений результативной переменной ЧП от ее значений, полученных по модели регрессии (предсказанных). Для оценки уровня точности используются различные ошибки: средняя относительная, стандартная и другие. Cтандартная ошибка модели 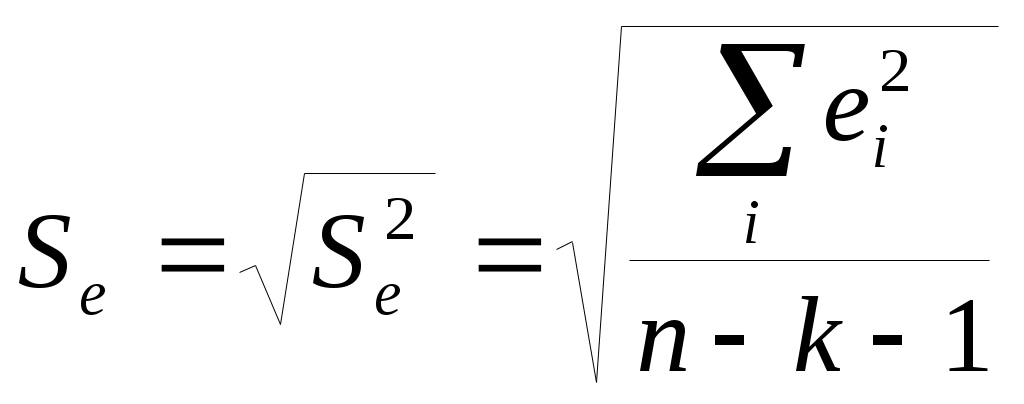 выводится в первой таблице «Регрессионная статистика» отчета по регрессионному анализу. Для нашей трехфакторной модели эта таблица представлена на рисунке 10.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||