Железобетонные конструкции одноэтажного двухпролётного промздания. Одноэтажное промышленное здание

• Название: Одноэтажное промышленное здание
• Анкор: Железобетонные конструкции одноэтажного двухпролётного промздания
• Дата: 01.03.2023
• Размер: 5.4 Mb.
• Имя файла: 18 м, В=6, Н=13,5.doc
• Тип: Литература; #962579
• страница: 3 из 8

1.7. Крановая нагрузка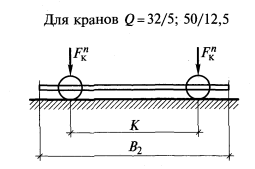



Рис.7. Схема крана

Таблица 2

Характеристики крана:





Кран мостовой электрический общего назначения г/п = 32/5 т для среднего режима работы: Q = 320 кН; В = 6,3 м; К = 5,1 м;

крановый рельс КР 70, высотой 120 мм.

Максимальное давление колеса: F_к = 235 кН;

Горизонтальная поперечная сила тормозная при гибком грузе:

Т = (Q+G_т)/40 = (320+87)/40 = 10,2 кН;

При _f = 1,1 максимальное и минимальное давления на колесо крана:

F_к = F_к*g_f*g_n = 235*1,2*1 = 312 кН, где

g_f=1,2 – для крановой нагрузки

g = 1 – для здания класса нормальной ответственности

Расчётная поперечная (горизонтальная) тормозная сила на 1 колесо, вызываемая торможением тележки:

Т_к = Т *g_f*g_n = 10,2 *1,2*1 = 12 кН.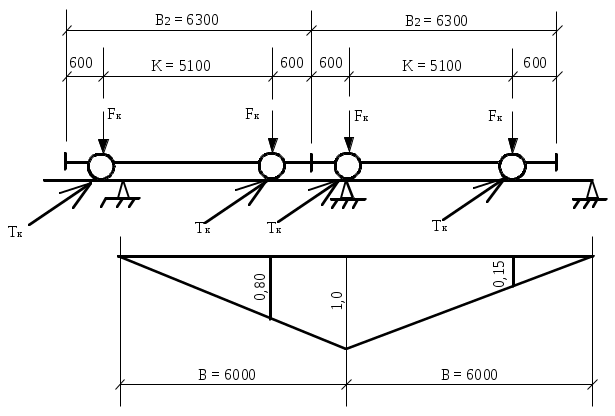



Рис. 8. Схема крана и ординаты линий влияния давления на колонну

Вертикальная крановая нагрузка на колонны от 2-х сближённых кранов с коэффициентом сочетаний g_с = 0,85:

D_max = F_к *g_с* у = 312*0,85*1,95 = 517 кН;

D_min = 517* 30/312= 50 кН, где

у = 0,8+1,0+0,15 = 1,95 м – сумма ординат линий влияния давления на колонну.

g_с = 0,85 – коэффициент сочетаний для 2-х кранов среднего режима работы [9, стр. 288].

F_k = (9,8*Q + G_к) / n₀ – F_к = (9,8*32 +250 ) / 2 – 312 = 30 кН, где

Q – грузоподъёмность крана,

G_к = 25 т = 250 кН - масса крана, см. характеристики.

n₀ = 2 кол-во колёс крана;

Горизонтальная крановая нагрузка на колонну от двух кранов при торможении:

H_max = Т_к *g_с* у = 12*0,85*1,95= 20 кН.

Усилия в колоннах от крановой нагрузки при возможных сочетаниях:

1.8. Расчётная схема рамы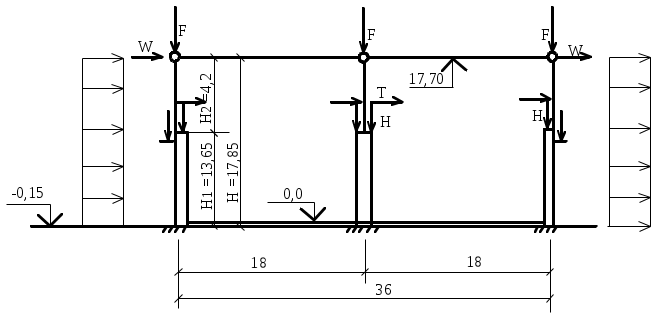



Рис. 9. Расчётная схема рамы с нагрузками на раму

2. Расчёт колонны крайнего ряда

2.1. Расчётные усилия в колонне

Рассматриваем 2 сечения рассчитываемой колонны:

сечение 1 – низ надкрановой части, на уровне верха консоли, отм. 13,5 м;

сечение 2 – низ подкрановой части колонны, у обреза фундамента, отм. -0,15 м.

Длительная часть нагрузки рассчитана с помощью коэффициента 1,2. Для сочетания одной постоянной и одной временной (снеговая) нагрузок принят коэффициент сочетаний ψ = 1 [1, п.6.4].

В сечении 1: М_ℓ =150/1,2 = 125 кН*м, N_ℓ = 1530/1,2 = 1275 кН.

В сечении 2: М_ℓ =150/1,2 = 125 кН*м, N_ℓ = 1530/1,2 = 1275 кН.



Рис. 10. Расчётная схема крайней колонны

2.2. Материалы

По заданию рассчитываемая колонна крайняя К1.

Расчёт выполнен по [15, С. 51-70].

Бетон по заданию тяжёлый класса В 40.

По [2, табл.6.7, 6.8, 6.11] расчётное сопротивление сжатию R_b = 22,0 МПа;

То же, растяжению R_bt = 1,4 МПа;

R_bt,ser = 2,1 МПа – расчётное сопротивление бетона для предельных состояний 2 группы.

Начальный модуль упругости бетона E_b = 36*10³ МПа.

Арматура класса продольная для ветвей и распорок А 300, расчётное сопротивление растяжению [2, ф-ла 6.10]

R_s = R_sc = R_sn/γ_s = 300/1,15 = 270 МПа, где

R_sn= 300 МПа – нормативное значение сопротивления растяжению по [2, табл. 6.14];

γ_s = 1,15 – коэффициент надёжности по арматуре [2, п.6.2.8];

модуль упругости E_s =2*10⁵ МПа [2, п.6.2.12];

поперечная арматура ветвей А 240, расчётное сопротивление растяжению

R_sw = 175 МПа [2, табл. 6.15], модуль упругости E_s =2*10⁵ МПа [2, п.6.2.12].

2.3. Сечение 1 – надкрановая часть, на уровне верха консоли.

Сечение колонны b x h = 60 x 50 см.

Колонна внецентренно-сжатая. Расчётная комбинация усилий: М = 70 кН*м;

N = 570 кН; Q не задана.

Длительно действующие постоянные нагрузки: М_ℓ = 58 кН*м; N_ℓ = 475 кН

Эксцентриситет от расчётной нагрузки:

e_о = М /N = 70*(100) / 570 = 12 см; он должен быть не меньше случайного.

Случайный эксцентриситет возникает всегда, даже в центрально-нагруженных стержнях. Он возникает от неравномерного натяжения арматуры, от неравномерного застывания бетона в формах, от разного диаметра армирования в сжатой и растянутой зонах сечения, от погрешностях, ошибках и неточности при бетонировании и армировании, а также при дополнительных несимметричных нагрузках при эксплуатации..

Случайный эксцентриситет из условий:

е_а  1 /30*h = 50 / 30 = 1,7 см;

е_а  1 /600*H₂ = 480 / 600 = 0,8 см;

е_а  1 см.

Принимаем для расчёта наибольшее значение: e_о = 12 см = 0,12 м  е_а,

e_о = 0,12 м  0,1*h = 0,1*0,5 = 0,05 м, случайный эксцентриситет можно не учитывать, т.к. колонна является элементом статически неопределимой системы.

Расчёт по предельным состояниям 1 группы

Расчет по предельным состояниям первой группы (по потере несущей способности или полной непригодности к эксплуатации) выполняют, чтобы обеспечить прочность, устойчивость, выносливость конструкций.

Расчёт в плоскости изгиба

Радиус инерции сечения i= = =14,4 см

ℓ₀ = ψ * Н₂ = 2*4,2 = 8,4 м – расчётная длина надкрановой части колонны при учёте крановых нагрузок, где

ψ = 2 – коэффициент для расчётной длины внецентренно сжатого элемента по [2, п. 8.1.17].

Гибкость в плоскости изгиба  = ℓ₀ / i = 8,4*(100) / 14,4 = 58 < [] =120 – в пределах допустимой для колонн [2, п.10.2.2].

 = 58 > 14, т. е. необходимо учесть влияние прогиба элемента на его прочность [2, п.7.1.8].

Момент инерции сечения J = b*h³ /12 = 60*50³ /12 = 625000 см³;

Принимаем привязку стержня рабочей арматуры а=4 см с учётом защитного слоя бетона не менее 20 мм по [2, п.10.3.1],

Для продольной арматуры (напрягаемой и ненапрягаемой) толщина защитного слоя должна быть не менее диаметра стержня и не менее:

- для конструкций в закрытых помещениях при нормальной и пониженной влажности - 20 мм;

- то же, при повышенной влажности и отсутствии дополнительных защитных мероприятий - 25 мм;

- для конструкций на открытом воздухе и отсутствии дополнительных защитных мероприятий - 30 мм.

Для поперечной, распределительной и конструктивной арматуры минимальная толщина защитного слоя принимается на 5 мм меньше указанной для рабочей продольной арматуры, и не менее диаметра стержня соответствующей арматуры.

Рабочая высота сечения h_o= h – а = 50 – 4 = 46 см.

Момент внешних сил относительно центра тяжести растянутой арматуры с учётом всех нагрузок:

М_ℓ = М + N*(0,5*h – a) = 150 + 1530*(0,5*0,5 – 0,04) = 471 кН*м;

То же, длительно действующей нагрузки:

М_1ℓ= М _ℓ + N _ℓ *(0,5*h – a) = 125 + 1275*(0,5*0,5 – 0,04) = 393 кН*м;

Т.к. крановые нагрузки учтены в сочетание нагрузок по [4, п.3.3.]

М_1ℓ = 393 кН*м < 0,9*М_ℓ = 0,9*471 = 424 кН*м, то

_b2 =1,1 – коэффициент условий работы бетона [15, С.63] при учёте крановой нагрузки.

Если М_1ℓ > 0,9*М_ℓ, то _b2 = 0,9 по [4, п.3.3.].

Коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии [4, п.3.10, ф-ла 3.9]:

j_ℓ = 1+β* М_1ℓ / М_ℓ = 1+1*393/471 = 1,8 < 2 при β=1 для тяжёлого бетона.

При j_ℓ > 2 принимать j_ℓ = 2.

Задаемся в первом приближении коэффициентом армирования  = 0,005 в пределах предельных процентов армирования для данного класса бетона

_е = е_о / h = 0,1 / 0,5 = 0,2 – коэффициент, принимаемый равным e_o/h, но не менее _е,min = 0,15 и не более _е,mах = 1,5 по [4, п.3.10].

Отношение модулей упругости арматуры и бетона:

 = Е_s / Е_b = 200000 / 36000 = 5,6

Условную критическую силу можно определить через жёсткость по [4, п.3.10]. Жёсткость элемента в предельной по прочности стадии для элементов прямоугольного сечения [4, п. 3.9, ф-ла 3.8а]: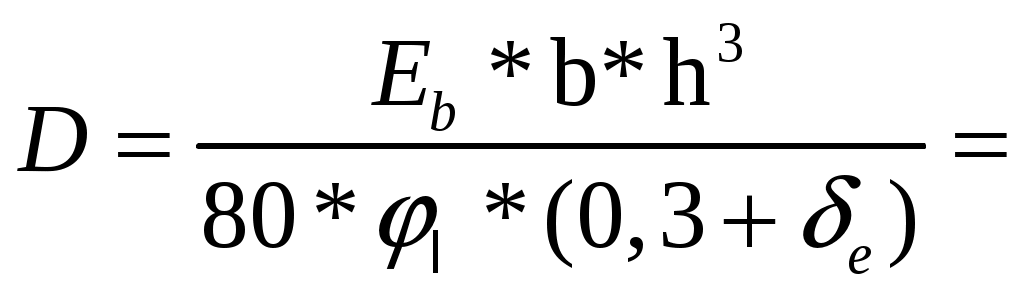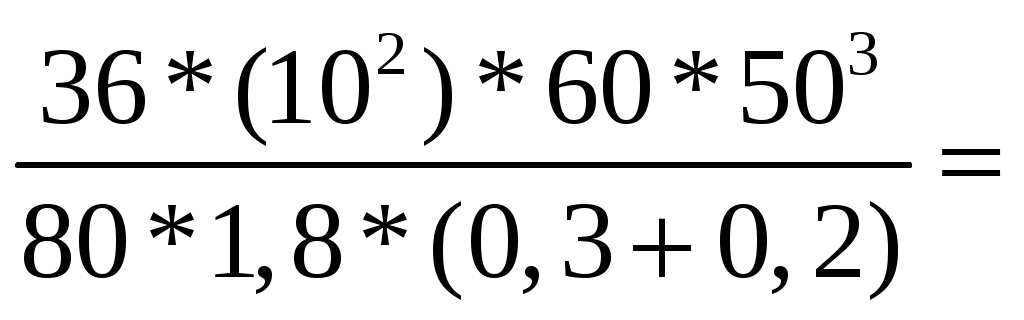

375*10⁶ кН*см²

Условная критическая сила [4, п. 3.9, ф-ла 3.7]: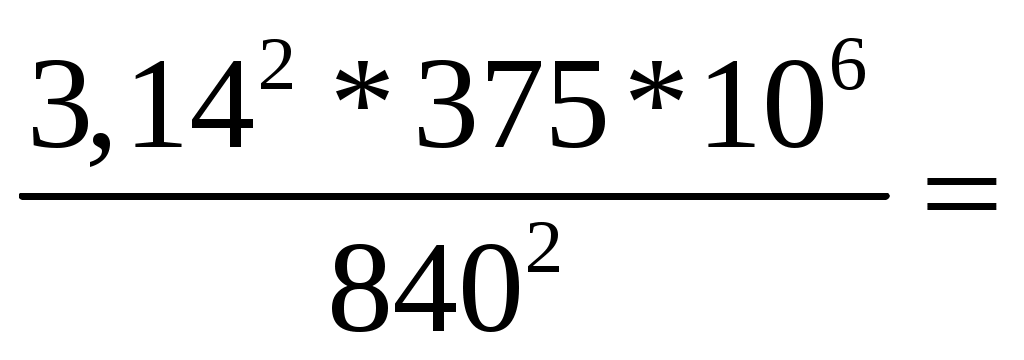

5240 кН

Принимаем для расчёта наименьшую из двух, поскольку эксцентриситет будет больше.

При N_cr > N размеры сечения достаточны.

Коэффициент увеличения начального эксцентриситета

 = 1 / (1 – N / N_cr) = 1 / (1 – 1530 /5240) = 1,41

Расчётный эксцентриситет продольной силы:

e = e_o* + (h₀ – a´)/2 = 10*1,41 + (46 – 4)/2 = 35 см.

Подбор продольной арматуры производят по [4, п. 3.21, ф-ла 3.22].

Для расчёта площади армирования прямоугольного сечения коэффициент _m по [4, п.3.21, ф-ла 3.22]:

 0,049 < a_R= 0,39, где

a_Rкоэффициент для арматуры А 300 по [4, табл. 3.2].

Если по расчёту α_т ≥ a_R, требуется увеличить сечение или повысить класс бетона, или установить сжатую арматуру. Требуемую площадь сечения определяем по формулам [4, п. 3.22, ф-ла 3.24, 3.25].

При α_т < a_R сжатая арматура по расчету не требуется, и тогда растянутая арматура определяется по [4, п. 3.21, ф-ла 3.23]:

= 12,6 см²

Принимаем в растянутой зоне надкрановой части колонны:

3  36 A 300 A_s = 30,54 см², больше расчётного и минимального.

В сжатой зоне арматура ставится конструктивно, т.к. по расчёту не требуется:

3  36 А 300 A_s' = 30,54 см² – армирование необходимо делать симметричное, одинаковое в сжатой и растянутой зонах, чтобы не добавлять эксцентриситеты.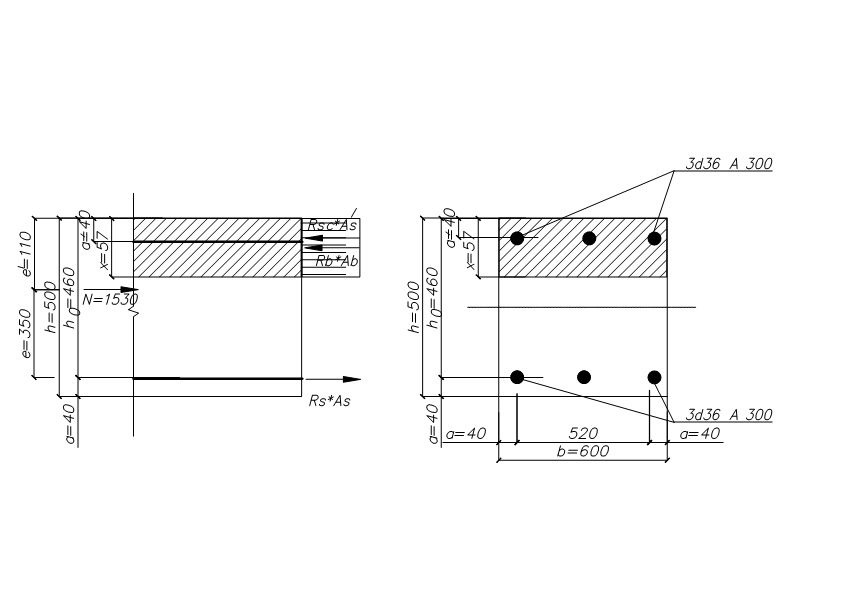

Рис. 11. Расчётная схема надкрановой части колонны

Расстояния между продольными стержнями армирования 260 мм ≤ 500 мм. Максимальное расстояние в плоскости изгиба между продольным армированием должно быть не более 500 мм [2, п.10.3.8] для равномерного распределения деформаций, ограничения ширины раскрытия трещин между стержнями.

Процент армирования всего сечения:

 = А_s /(b*h₀) = 37,7*(100)/(60*46) = 1,4 % , в пределах допустимых норм по [ 9, табл. 12, 13, С.184 ]:

_min = 0,2 % = 0,002, _maх = 4,0 % = 0,04

Высота сжатой зоны прямоугольного сечения [4, п.3.18, ф-ла 3.16]:

х = 5,7 см,

расчёт производим без учёта сжатой арматуры, A_s'=0 – т.к. она не нужна по расчёту.

Относительная высота сжатой зоны  = x / h_o = 5,7 / 46 = 0,12 по [4, п.3.17].

Граничная относительная высота сжатой зоны бетона по [3, ф-ла 8.1]:

_R = х_R/h₀ = 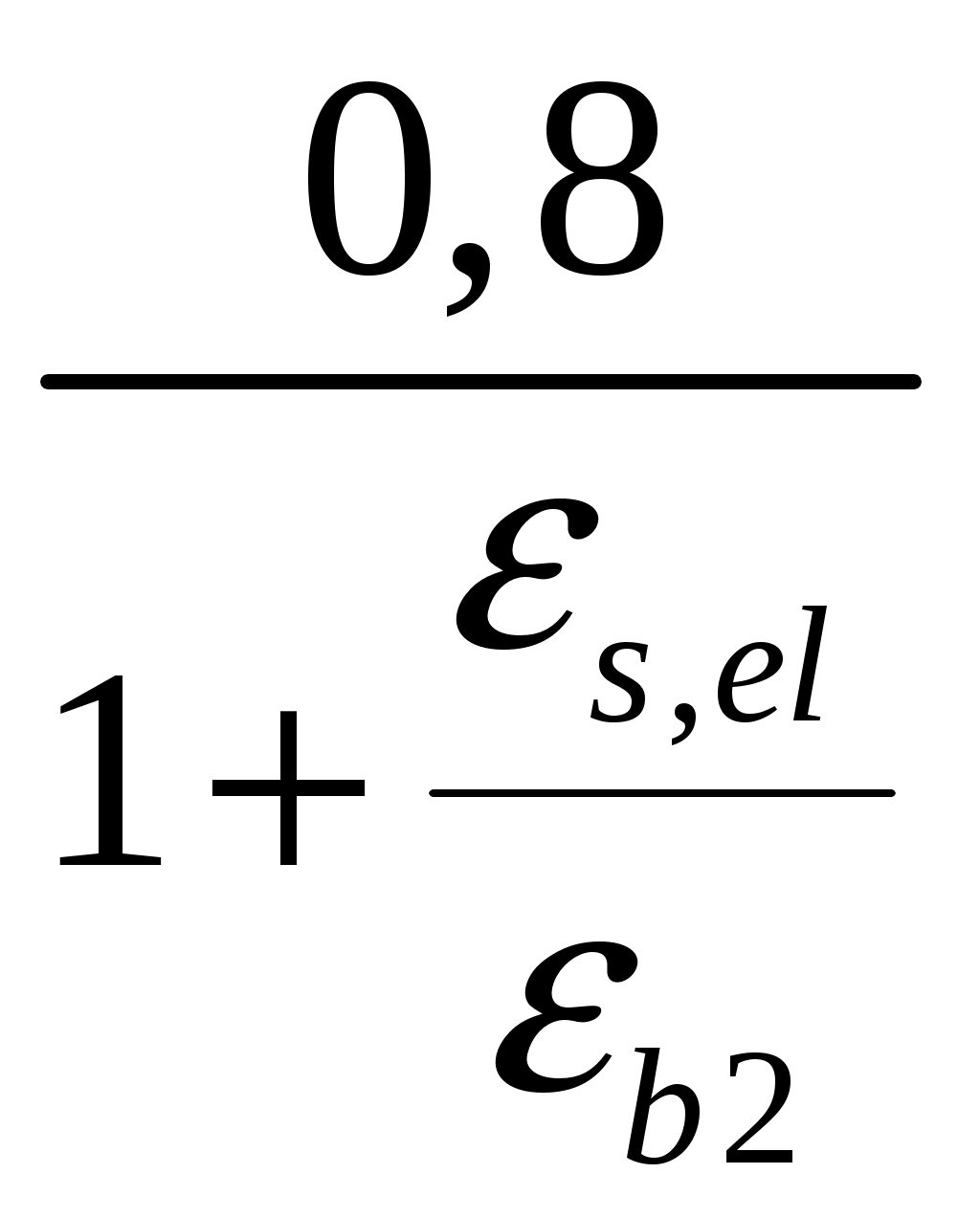= = 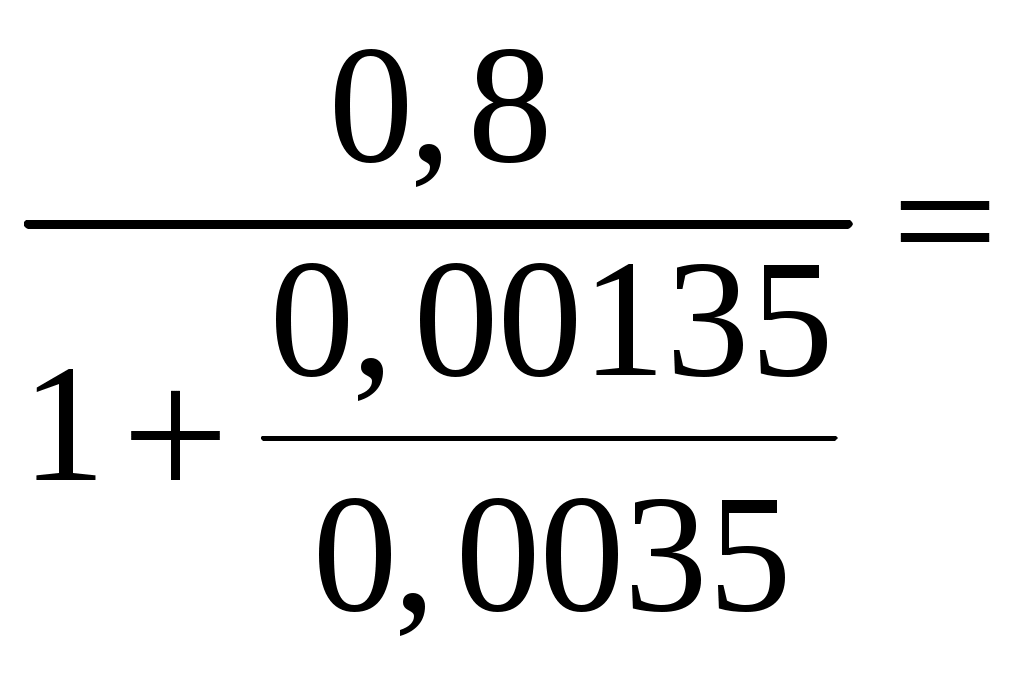0,577

= R_S/E_S = 270/200000 = 0,00135 - относительная деформация растянутой арматуры при напряжениях равных R_S по [3, ф-ла 8.2];

= 0,0035 - относительная деформация сжатого бетона при напряжениях, равных R_b [5, п.6.1.20] для классов бетона ниже В 60.

_R также можно определить без расчёта, по таблице [4, табл.3.2]:

Для класса А 300 _R = 0,577, А 400 _R = 0,533

 = 0,12 ≤ _R = 0,577 условия прочности изгибаемых элементов [2, п.8.1.4 - 8.1.12] соблюдены. В случае  > _R, расчет прямоугольных сечений производится по [4, п.3.18, ф-ла 3.18].

В случае эксцентриситета продольной силы e ≤ h / 30 и гибкости ℓ₀ / h ≤ 20 расчет по прочности прямоугольных сечений внецентренно сжатых элементов с арматурой, расположенной у противоположных в плоскости изгиба сторон сечения, допускается производить из условия [2, ф-ла 8.16, п.8.1.16] , [3, п.6.2.17, ф-лы 6.26, 6.27]: N ≤ N_uℓt

В данном случае: e = 35 см > h/30 = 50/30 = 1,7 см,

гибкость  = ℓ₀ / h = 8,4*(100)/50 = 17 < 20 – проверку производим.

N_ult - предельное значение продольной силы, которую может воспринять элемент, определяемое по формуле [3, ф-ла 6.27]:

N_uℓt = φ*(R_b*А+ R_sc*A_{s, tot}) = 0,73*[(22*(10^-1)*3000+270*(10^-1)*61] = 6022 кН, где А = b* h = 60*50 = 3000 см² – площадь сечения,

A_s,tot - площадь всей продольной арматуры в сечении (сжатой и растянутой):

A_s,tot = A_s + А_s = 30,54+30,54 = 61 см²

φ = 0,73 - коэффициент, принимаемый при длительном действии нагрузки по [3, табл. 6.2] в зависимости от гибкости элемента ℓ₀ / h = 19, интерполяцией.

N= 1530 кН ≤ N_uℓt = 6022 кН.

Прочность сечения по продольному усилию обеспечена.

l₀ - расчетная длина элемента, определяемая как для железобетонных элементов.

В данном случае: e = 35 см > h/30 = 60/30 = 2 см

ℓ₀ = 840 см ≤ 20*h = 20*60 = 1200 см,

Расчет внецентренно сжатых железобетонных элементов без предварительного напряжения производят из условия [5, п. 7.1.9, ф-ла 8.10]:

N*е ≤ R_b*b*х*(h₀ – 0,5*х)+R_sc*А_s'*(h₀ – а'),

N*е = 1530*35 = 53550 кН*см ≤ 22*(10^-1)*60*5,7*(46 – 0,5*5,7)+

+ 270*(10^-1)*30,54*(46 – 4) = 67098 кН*см, где

N - действующая продольная сила от внешней нагрузки.

Условие прочности по продольному усилию с эксцентриситетом соблюдается с запасом по прочности.

Из данных проверок прямоугольного сечения видно, что армирования достаточно.

При несоблюдении данных условий проверок надо увеличить: армирование, размеры сечения или классы бетона и арматуры.

Расчёт из плоскости изгиба

При расчёте верхней части из плоскости изгиба (в плоскости, перпендикулярной к плоскости изгиба) за высоту сечения принята его ширина.

ℓ_o = ψ * Н₂= 1,5*4,2 = 6,3 м = 630 см, где

ψ = 1,5 – коэффициент для расчётной длины внецентренно сжатого элемента по [1, п. 8.1.17].

Момент инерции i'= = =17,3 см.

Гибкость из плоскости изгиба ' = ℓ_o / i' = 630 / 17,3 = 36 < [] =120 – в пределах допустимой для колонн [2, п.10.2.2].

' = 36 <  = ℓ_o / i = 58, меньше гибкости, чем в плоскости изгиба.

Т.к. гибкость из плоскости момента меньше гибкости в плоскости действия момента, расчёт можно не выполнять, т.к. по расчёту армирование будет ещё меньше.

Не предусматриваем дополнительное конструктивное продольное армирование из плоскости, т.к. расстояния между продольными стержнями из плоскости изгиба не превышают 400 мм [2, п.10.3.8].