Железобетонные конструкции одноэтажного двухпролётного промздания. Одноэтажное промышленное здание

• Название: Одноэтажное промышленное здание
• Анкор: Железобетонные конструкции одноэтажного двухпролётного промздания
• Дата: 01.03.2023
• Размер: 5.4 Mb.
• Имя файла: 18 м, В=6, Н=13,5.doc
• Тип: Литература; #962579
• страница: 4 из 8

Расчёт поперечного армирования

Максимальная поперечная сила Q_maх не задана заданием.

Поперечную арматуру принимаем из условий [16, прил.8, С. 844], [2, п.10.3.12…10.3.14]:

для продольной арматуры d 36 мм по условию сварки минимально допустимый диаметр поперечной арматуры d_w = 10 мм,

не менее 0,25*d = 0,25*36 = 9 мм.

Принят d_w = 10 мм A 240.

Шаг стержней по [2, п.10.3.13]:

- не более 0,75*h = 0,75*60 = 40 см,

- не более 500 мм,

- не более 20*d=20*36 = 720 мм – для предотвращения выпучивания продольной

Принят s = 40 см.

В верхней части колонны ставим сетки С 2 4 шт с шагом S=50 мм и закладную деталь М 1 для опирания фермы на оголовок колонны.

Стержни сетки С 2 принимаем из арматуры класса А 240.

Расчёт по предельным состояниям 2 группы

Расчет по предельным состояниям второй группы выполняют по образованию трещин, по раскрытию трещин (если они образуются), по деформациям (прогибы и перемещения).

Расчёт по образованию трещин

Геометрические характеристики сечения:

Площадь приведённого сечения [2, ф-ла 8.126]:

A_red = A + * A_s + * A'_s = 60*50 + 5,6*30,54 + 5,6*30,54 = 3342 см², где

A_, A_s, A'_s - площади поперечного сечения бетона, растянутой и сжатой арматуры соответственно.

 = Е_s / Е_b = 200000 / 36000 = 5,6

Момент инерции сечения относительно горизонтальной оси, проходящей через его центр тяжести [2, ф-ла 8.125]:

J_red= J + J_s *α+ J'_s *α = 2500000 +13468*5,6+13468*5,6 = 2650843 см⁴

J_, J_s, J'_s - моменты инерции сечений бетона, растянутой арматуры и сжатой арматуры соответственно;

J = b*h³/12+ b*h*у² = 60*50³/12 + 60*50*25² = 2500000 см⁴

J_s = J'_s = A_s *(у – а)² = 30,54*(25 – 4)² = 13468 см⁴

у_i – расстояние от центра тяжести до нижней границы:

у₁ = 50/2 =25 см,

Статический момент относительно нижней грани:

S_red = A_i*у_i = 60*50*25 + 30,54*5,6*4 + 30,54*5,6*4 = 76368 см², где

привязка стержня а = у₂ = 4 см.

у = S_red / A_red = 76368/3342 = 23 см - расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента, в данном случае сечение прямоугольное и симметричное;

W_red =J_red/у = 2650843/23 = 115254 см³ - упругий момент сопротивления приведенного сечения по растянутой зоне сечения, определяемый в соответствии с [2, п.8.2.12].

W_pℓ - упругопластический момент сопротивления сечения для крайнего растянутого волокна бетона, определяемый с учетом [2, п. 8.2.10]:

для прямоугольного сечения упругопластический момент сопротивления относительно нижней грани:

W_pℓ = 1,3*W_red = 1,3 * 115254 = 149830 см³.

е_х=W_red/A_red = 115254/3342= 34,5 см- расстояние от точки приложения продольной силы  (расположенной в центре тяжести приведенного сечения элемента) до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется [2, ф-ла 8.124].

Расчёт по образованию трещин производится из условия: M  M_crc [2, ф-ла 8.116]:

М = 150 кН*м ≤ M_crc = R_bt,ser*W_pℓ ± N*е_х = 2,1*(10^-1) *149830 ± 1530*34,5 =

= 31464 ± 52764 = 36728 кН*см = 367 кН*м, где

M_crc - изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый по ф-ле [2, ф-ла 8.121].

Расчёт по образованию трещин выполнен, трещины не образуются, значит, не надо делать расчёт по раскрытию трещин.

2.3. Сечение 2 – подкрановая часть, в заделке колонны.

Высота сечения нижней части колонны крайнего ряда h = 130 см,

сечение каждой ветви 60 x 30 см,

расстояние между центрами ветвей с = 0,7 +0,3 = 1,0 м;

высота ветви между распорками Н_р = 3,0 м; высота распорки h_р = 45 см,

расстояние между осями распорок S = Н_р+ h_р = 3,0+0,45 = 3,45 м.

Расчётная комбинация усилий: М = 150 кН*м; N= 1530 кН; Q= 0 кН;

Длительно действующие нагрузки: М_ℓ= 125 кН*м, N_ℓ = 1275 кН.

Расчёт по предельным состояниям 1 группы

Расчёт в плоскости изгиба

Сначала рассматриваем всё составное сечение, как единое целое, затем рассчитываем каждую ветвь подкрановой части.

Расчётная длина подкрановой части при учёте крановых нагрузок

ℓ_o = *H₁ = 1,5*13,65 = 20,5 м, где

ψ = 1,5 – коэффициент для расчётной длины внецентренно сжатого элемента по [2, п. 8.1.17], для элемента с жёсткой без поворота заделкой на одном конце (в фундамент) и податливое шарнирное опирание, допускающее ограниченное смещение опоры на другом (заделка в надкрановую часть).

Принимаем привязку стержня рабочей арматуры а=4 см с учётом защитного слоя бетона не менее 20 мм по [2, п.10.3.1],

рабочая высота сечения h_o= h – а = 130 – 4 = 56 см.

Момент внешних сил относительно центра тяжести всего подкранового сечения для растянутой арматуры с учётом расчётных нагрузок:

М_ℓ = М + N*(0,5*h – a) = 150 + 1530*(0,5*1,3 – 0,04) = 1083 кН*м;

То же, длительно действующей нагрузки:

М_1ℓ = М_ℓ + N_ℓ*(0,5*h – a) = 125 + 1275*(0,5*1,3 – 0,04) = 903 кН*м;

Т.к. крановые нагрузки учтены в сочетание нагрузок по [4, п.3.3.]:

М_1ℓ = 903 кН*м ≤ 0,9*М_ℓ = 0,9*1083 = 975 кН*м, то

Если М_1ℓ ≤ 0,9*М_ℓ, то _b2 =1,1 по [10, С.63], если М_1ℓ > 0,9*М_ℓ то _b2 = 0,9 – коэффициент условий работы бетона при учёте крановой нагрузки по [4, п.3.3.].

Приведенную гибкость подкрановой части определим как для стержня составного сечения по [15, ф-ла 3.3, С.65]:

4* ℓ_o² / с²+12*S²/h_br² = 4*20,5²/1,0²+12*3,45²/0,3² = 3268

Приведенная гибкость двухветвевой колонны в плоскости изгиба:

λ_red = ℓ_o / i_red = = 57 < [] =120 – в пределах нормы для колонн [2, п.10.2.2].

при λ_red = 57> 14 необходимо учесть влияние прогиба элемента на его прочность.

Случайный эксцентриситет всей подкрановой ветви из условий [4, п.3.6]:

е_а  1 /30*h = 130 / 30 = 4,3 см;

е_а  1 /600*S = 345 / 600 = 0,6 см;

е_а  1 см.

Проектный эксцентриситет всей подкрановой части колонны:

е_о = М/ N = 150*(100) / 1530 = 10 см ≥ е_а = 4,3 см.

e_о = 0,1 м < 0,1*h₁= 0,1*1,3 = 0,13 м, принимается для расчётов наибольшее значение эксцентриситета e_о= 0,13 м, случайный эксцентриситет можно не учитывать, т.к. колонна является элементом статически неопределимой системы.

Коэффициент, учитывающий длительное действие нагрузки [4, п.3.10, ф-ла 3.9]:

j_ℓ = 1+β*М_1ℓ / М_ℓ = 1+1*903/1083 = 1,83 < 2 (не более 2),

β=1 для тяжёлого бетона.

Задаемся в первом приближении коэффициентом армирования  = 0,005 в пределах предельных процентов армирования. По [16, табл.12, 13, С.184] для бетона В 40 и арматуры А 300 для внецентренно сжатых элементов при

35 ≤ _red = ℓ₀ / i_red = 57 ≤ 83 предельные проценты армирования:

_min = 0,2 % = 0,002, _maх = 4,0 % = 0,04

Принимаем коэффициент армирования _min = 0,5 % = 0,005

_е = е_о / h₁ = 0,1 / 1,3 = 0,08 < 0,15 – коэффициент, принимаемый равным e_o/h, но менее _е,min = 0,15 и не более _е,mах = 1,5 по [4, п.3.10], следовательно, принимаем для расчёта наибольшее значение _е = 0,15

Отношение модулей упругости арматуры и бетона:

_s = Е_s / Е_b = 200000 / 36000 = 5,6

Условная критическая сила по [16, С. 66] для составного сечения колонны с высотой сечения одной ветви h = h_br: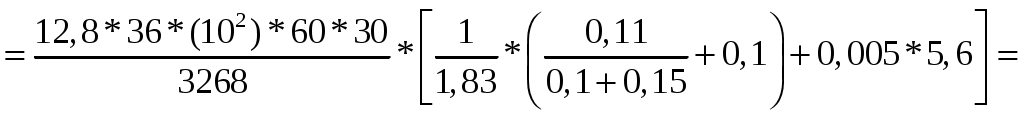



8200 кН

При N_cr > N размеры сечения достаточны, увеличивать не нужно.

Условную критическую силу можно определить также через жёсткость по [4, п.3.10]. Жёсткость элемента в предельной по прочности стадии для любых сечений [4, п. 3.9, ф-ла 3.8]: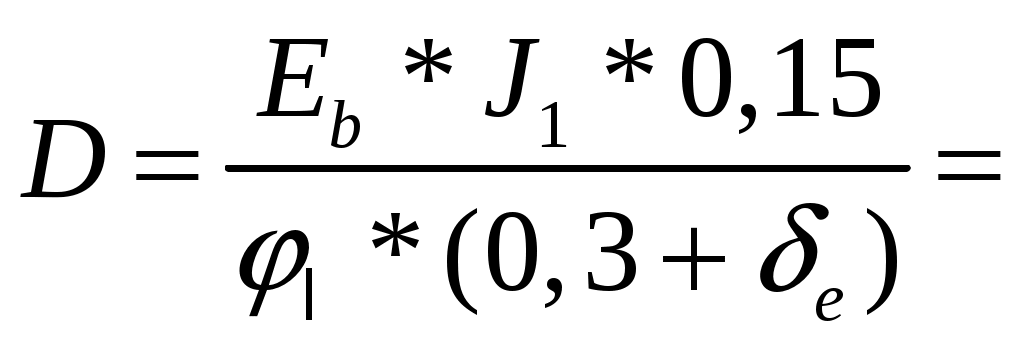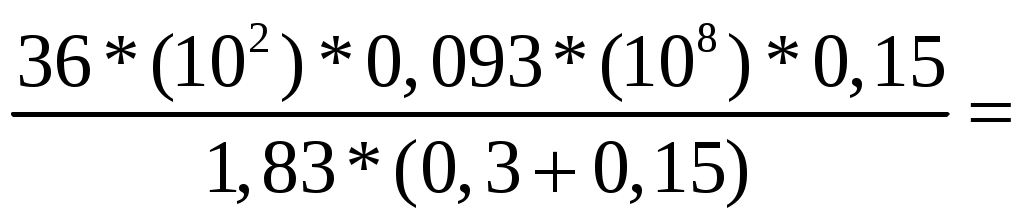

6098,4*10⁶ кН*см² где

J₁ = b*(h₁³– h_1p³)/12= 0,6*(1,3³– 0,7³)/12= 0,093 м⁴ = 0,093*(10⁸) см⁴ – геометрические параметры сечения крайней колонны каркаса – момент инерции,

h₁ = 1,3 м,

h_1p = h₁ – 2*h_1b = 1,3 – 2*0,3 = 0,7 м.

Условная критическая сила [4, п. 3.9, ф-ла 3.7]: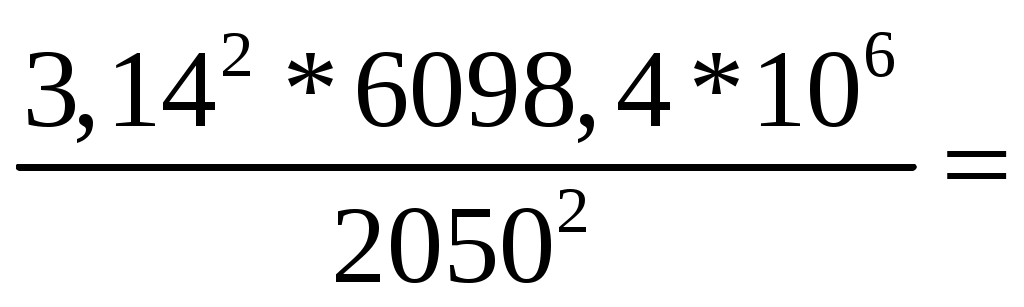

14308 кН

Принимаем для расчёта наименьшую из двух, поскольку в таком случае эксцентриситет будет больше. Коэффициент увеличения начального эксцентриситета [2, ф-ла 8.14], [3, ф-ла 6.6]:

 = 1 / (1 – N / N_cr) = 1 / (1 – 1530 /8200) = 1,23.

Далее ведём расчёт на одну ветвь подкрановой части – наиболее нагруженную.

b х h = 60 x 30 см, рабочая высота сечения h_o= h – а = 30 – 4 = 26 см.

Распределяем заданные усилия между элементами подкрановой части колонны – ветвями и распорками. В целях упрощения принимаем, что продольные силы распределяются между ветвями по закону рычага, а нулевые точки моментов в ветвях расположены в середине высоты панели [15, С. 66].

Усилия в ветвях колонны по [15, С.66]:

N_br = N / 2  M* / c = 1530 / 2  150*1,23 / 1,0 = 765  185 кН

Внутренняя ветвь подкрановой части наиболее нагруженная, на неё опирается подкрановая балка: N_br1 = 765 + 185 = 950 кН.

Наружная ветвь подкрановой части наименее нагруженная, на неё навешиваются

стеновые панели: N_br2 = 765 – 185 = 580 кН.

Это для колонн крайних рядов. Для всех колонн средних рядов обе ветви подкрановые и нагружены одинаково симметрично.

Момент от местного изгиба ветвей при нулевой точке моментов в середине высоты панели (посередине распорки) по [15, стр.66], [17, ф-ла 13.37, стр.404]:

М_br = Q*S / n = Q*3,45 / 4, где

n=4 – число отверстий в подкрановой ветви.

Поскольку в исходных данных нет значения поперечной силы, находим момент другим способом, деля расчётный на кол-во ветвей:

М_br1 = М_br2 = М / 2 = 150/2 = 75 кН

Случайный эксцентриситет одной ветви подкрановой части:

е_а = 1 /30* h_br = 30 / 30 = 1,0 см;

е_а = 1 /600*S = 345 / 600 = 0,6 см;

Проектный эксцентриситет внутренней ветви подкрановой части от расчётных усилий:

e_о1 = М_br1 / N_br1 = 75*(100) / 950 = 7,9 см;

То же, наружной ветви:

e_о2 = М_br2 / N_br2 = 75*(100) / 580 = 12,9 см;

Расчётный эксцентриситет подкрановой части от продольной силы [16, С.66]:

внутренней ветви е₁ = е_о1 + h_br / 2 – a = 7,9 + 30 / 2 – 4 = 19 см,

наружной ветви: е₂ = е_о2 + h_br / 2 – a = 12,9 + 30 / 2 – 4 = 24 см,

М_br1 = N_br1*е₁= 950*19 = 18050 кН*см – момент во внутренней ветви подкрановой части от эксцентриситета [15, С. 67].

М_br2 = N_br2*е₂ = 580*24 = 13920 кН*см – момент в наружной ветви подкрановой части от эксцентриситета [15, С. 67].

Подбор продольной арматуры производят по [4, п. 3.21]. Для расчёта площади армирования прямоугольного сечения коэффициент _m по [4, п.3.21, ф-ла 3.22]:

_m1 = М_br1 / (_b2*R_b*b*h_o²) = 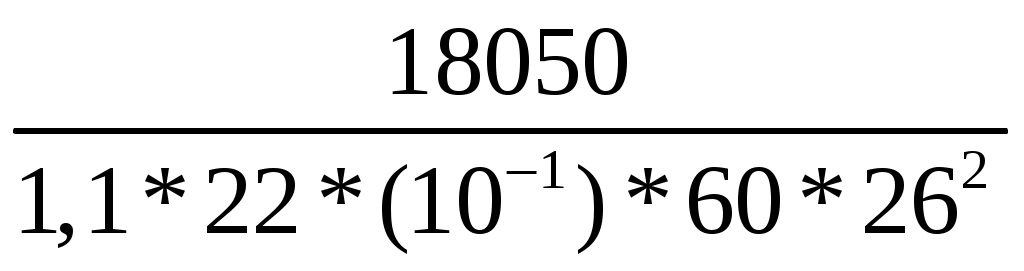= 0,184 < a_R= 0,411,

_m2 = М_br2 / (_b2*R_b*b*h_o²) = 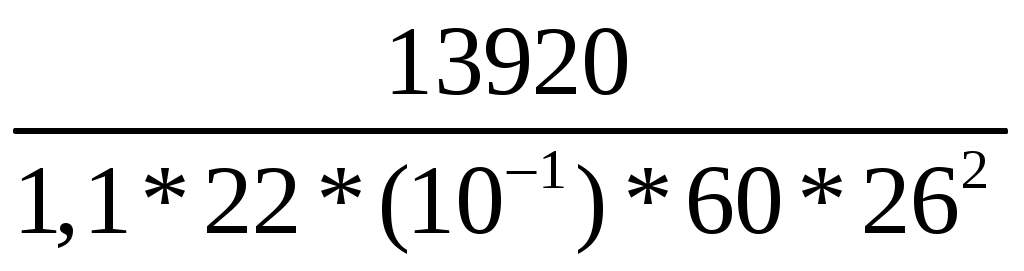= 0,142 < a_R= 0,411, где

α_R = 0,411 для продольной арматуры А 300 – по заданию [4, табл. 3.2].

Если α_т ≥ a_R, требуется и сжатая и растянутая арматуры, требуемую площадь сечения определяем по формулам [4, п. 3.21, п. 3.22, ф-ла 3.24, 3.25].

При α_т < a_R сжатая арматура по расчету не требуется, а растянутая арматура определяется по [4, ф-ла 3.23]:

=29 см²

=21 см²

Принимаем 3 стержня в растянутой зоне подкрановой ветви колонны:

3  36 A 300 A_s = 30,54 см², больше расчётного и минимального.

Армирование в растянутой и сжатой зонах делаем симметричное, чтобы не возникали лишние эксцентриситеты.

В сжатой зоне арматура ставится конструктивно, т.к. по расчёту не требуется,

3  36 A 300 A_s' = 30,54 см².

Итого по 6 стержней в каждой ветви 6  36 A 300. Всего 12 стержней во всей подкрановой части.

Процент армирования каждой ветви:

 = А_s /(b*h₀) = 30,54*(100)/(60*26) = 1,9 % ≥ _min= 0,1 %

 = 1,9 % ≤ _mах = 4 % – в пределах допустимых норм [16, табл.12, 13, С.184].

Расстояния между продольными стержнями армирования 260 мм ≤ 500 мм. Максимальное расстояние в плоскости изгиба между продольным армированием должно быть не более 500 мм [2, п.10.3.8] для равномерного распределения деформаций, ограничения ширины раскрытия трещин между стержнями.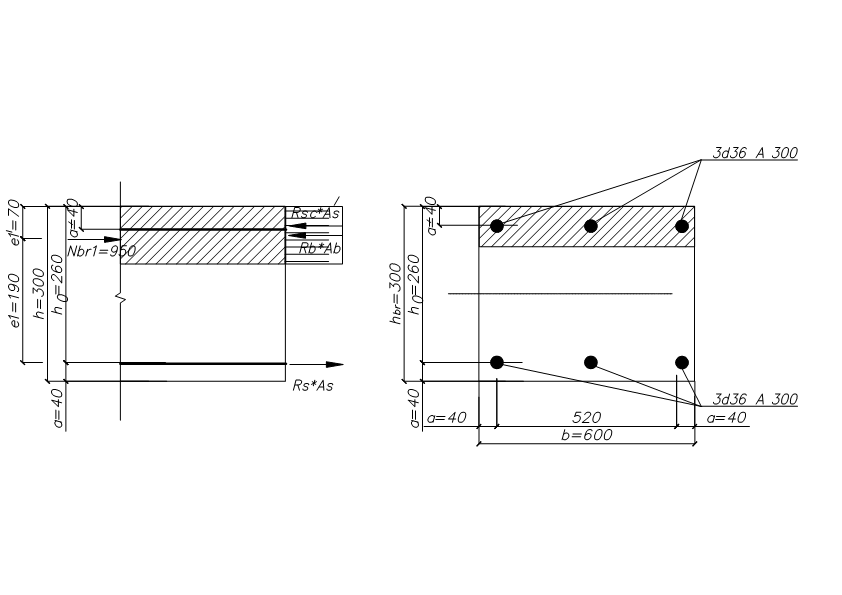



Рис. 12. Расчётное сечение внутренней ветви подкрановой части колонны

Производим проверку по несущей способности сечения из условия [2, ф-ла 8.16, п.8.1.16] , [3, п.6.2.17, ф-лы 6.26, 6.27]: N ≤ N_uℓt

N_ult - предельное значение продольной силы, которую может воспринять элемент, определяемое по формуле [3, ф-ла 6.27]:

N_uℓt = φ*( R_b*А+ R_sc*A_{s, tot}) = 0,82*[(22*(10^-1)*3600+270*(10^-1)*61,0] = 7845 кН, где А = b* h = 2*60*30 = 3600 см² – площадь сечения бетона – две ветви,

A_s,tot - площадь всей продольной арматуры в сечении (сжатой и растянутой):

A_s,tot = A_s + А_s = 30,54+30,54 = 61,0 см²

φ = 0,82 - коэффициент, принимаемый при длительном действии нагрузки по [3, табл. 6.2] в зависимости от гибкости элемента

ℓ₀ / h = 20,5*(100)/130=16, интерполяцией.

N = N_br1 + N_br2 = 1530 кН ≤ N_uℓt = 7845 кН.

Прочность сечения по продольному усилию обеспечена.

l₀ - расчетная длина элемента, определяемая как для железобетонных элементов.

В данном случае: e = 24 см > h/30 = 30/30 = 1 см

ℓ₀ = 2050 см > 20*h = 20*30 = 600 см,

Высота сжатой зоны прямоугольного сечения [4, п.3.18, ф-ла 3.16]:

х = 5,7 см,

расчёт производим без учёта сжатой арматуры, A_s'=0 – т.к. она не нужна по расчёту.

Расчет внецентренно сжатых железобетонных элементов без предварительного напряжения производят из условия [5, п. 7.1.9, ф-ла 8.10]:

N*е ≤ R_b*b*х*(h₀ – 0,5*х)+R_sc*А_s'*(h₀ – а'),

По данной формуле рассчитаем каждую ветвь:

N_br1*е₁ = 950*19 = 18050 кН*см ≤ 22*(10^-1)*60*5,7*(26 – 0,5*5,7)+

+ 270*(10^-1)*30,54*(26 – 4) = 35820 кН*см

N_br2*е₂ = 580*24 = 13920 кН*см ≤ 22*(10^-1)*60*5,7*(26 – 0,5*5,7)+

+ 270*(10^-1)*30,54*(26 – 4) = 35820 кН*см, где

N - действующая продольная сила от внешней нагрузки.

Условие прочности по продольному усилию с эксцентриситетом в каждой ветви соблюдается с запасом по прочности.