Оглавление 3 Примеры использования вычислительных средств Openfoam 1 1 Обтекание цилиндра 2

• Название: Оглавление 3 Примеры использования вычислительных средств Openfoam 1 1 Обтекание цилиндра 2
• Дата: 02.02.2023
• Размер: 1.64 Mb.
• Имя файла: 1111.doc
• Тип: Глава; #917307
• страница: 4 из 5

3.4 Декомпрессия резервуара с водой под избыточным внутренним давлением

В этом примере мы рассмотрим задачу быстрого открытия вентиля на трубке резервуара, наполненного жидкостью под избыточным внутренним давлением. Отличительным свойством решения в подобных случаях является распространение волн давления, которые поэтому нужно моделировать в условиях для сжимаемой жидкости.

Этот учебный материал вводит следующие новые возможности OpenFOAM:

• Улучшение сетки

• Волны давления в жидкостях

3.4.1 Постановка задачи

Область решения Область имеет 2 измерения и состоит из бака с небольшой трубкой для вытекания, как показано на Рис. 3.9.
Главныеуравнения

Для этой задачи требуется модель сжимаемости ψ жидкости для возможности решения распространения волн с конечной скоростью. Для того, чтобы связать плотность ρ, давление p и ψ, используется баротропное соотношение.

•Уравнение неразрывности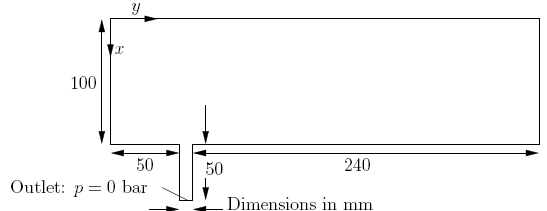

(3.14)


Размеры в мм

Примечание: изображение повернуто на -90^◦ от вертикали

Рисунок 3.9: Геометрия резервуара с выходной трубкой

• Баротропное соотношение

(3.15)

где K – модуль объемной упругости

• Уравнение 3.15 линеаризовано следующим образом

(3.16)

где ρ0 и p0 – эталонные данные для плотности и давления соответственно

ρ(p0) = ρ0.

•Уравнение количества движения для Ньютоновской жидкости

(3.17)

Граничныеусловия

При помощи FoamX можно установить следующие физические граничные условияt:

• условия для стенки обозначены как outerWall;

• оси обозначены как symmetryPlane;

• сопло обозначено как pressureOutlet, где p = 0 bar;

• передние и задние границы обозначены как пустые.
Начальные условияU = 0 м/с, p = 100 bar.
Свойства переноса

• Динамическая вязкость воды μ = 1.0 мПa с
Термодинамические свойства

• Плотность воды ρ = 1000 кг/м³

• Опорное давление p0 = 1 bar

• Сжимаемость воды ψ = 4.54 × 10⁻⁷ с²/м²
Название солвера sonicLiquidFoam: код для расчета звукового ламинарного течения сжимаемой жидкости.
Название примера пример decompressionTank (декомпрессионный резервуар) находится в директории $FOAM TUTORIALS/sonicLiquidFoam.

3.4.2 Генерация сетки

В этом примере моделируется полная геометрия; набор вершин и блоков дан ниже в файле описания сетки:

8 FoamFile

9 {

10 version 2.0;

11 format ascii;

12 class dictionary;

13 object blockMeshDict;

14 }

15 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

16

17 convertToMeters 0.1;

18

19 vertices

20 (

21 (0 0 -0.1)

22 (1 0 -0.1)

23 (0 0.5 -0.1)

24 (1 0.5 -0.1)

25 (1.5 0.5 -0.1)

26 (0 0.6 -0.1)

27 (1 0.6 -0.1)

28 (1.5 0.6 -0.1)

29 (0 3 -0.1)

30 (1 3 -0.1)

31 (0 0 0.1)

32 (1 0 0.1)

33 (0 0.5 0.1)

34 (1 0.5 0.1)

35 (1.5 0.5 0.1)

36 (0 0.6 0.1)

37 (1 0.6 0.1)

38 (1.5 0.6 0.1)

39 (0 3 0.1)

40 (1 3 0.1)

41 );

42

43 blocks

44 (

45 hex (0 1 3 2 10 11 13 12) (30 20 1) simpleGrading (1 1 1)

46 hex (2 3 6 5 12 13 16 15) (30 5 1) simpleGrading (1 1 1)

47 hex (3 4 7 6 13 14 17 16) (25 5 1) simpleGrading (1 1 1)

48 hex (5 6 9 8 15 16 19 18) (30 95 1) simpleGrading (1 1 1)

49 );

50

51 edges

52 (

53 );

54

55 patches

56 (

57 wall outerWall

58 (

59 (0 1 11 10)

60 (1 3 13 11)

61 (3 4 14 13)

62 (7 6 16 17)

63 (6 9 19 16)

64 (9 8 18 19)

65 )

66 symmetryPlane axis

67 (

68 (0 10 12 2)

69 (2 12 15 5)

70 (5 15 18 8)

71 )

72 patch nozzle

73 (

74 (4 7 17 14)

75 )

76 empty back

77 (

78 (0 2 3 1)

79 (2 5 6 3)

80 (3 6 7 4)

81 (5 8 9 6)

82 )

83 empty front

84 (

85 (10 11 13 12)

86 (12 13 16 15)

87 (13 14 17 16)

88 (15 16 19 18)

89 )

90 );

91

92 mergePatchPairs

93 (

94 );

95

96 // ************************************************************************* //
Для улучшения численной точности мы используем опорное значение в 1 бар для поля давления. Заметим, что как величина внутреннего поля , так и граничные условия являются суперпозицией решения и опорного уровня.

3.4.3 Подготовка к выполнению решения

Перед началом задания условий решения нам нужно рассмотреть характеристическую скорость явления, которое мы хотим уловить. В этом случае рассматриваемая скорость жидкости очень мала, но волна давления распространяется со скоростью звука в воде. Скорость звука вычисляется как: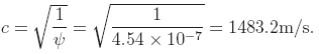

(3.18)

Для описанной выше сетки характеристический размер приблизительно равен 2 мм (заметим, что масштабирующий коэффициент 0.1 в файле blockMeshDict). С помощью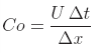

(3.19)

Разумный временной шаг составит около сек, задавая таким образом число Куранта Co, равным 0.35 с учетом скорости звука. Также заметим, что это число Co по коду (связанное с конвективной скоростью) меньше по величине на два порядка. Так как нас интересует распространение волны давления, мы установим время моделирования 0.25 мс. Для справки файл controlDict приводится ниже.



8 FoamFile

9 {

10 version 2.0;

11 format ascii;

12 class dictionary;

13 object controlDict;

14 }

15 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

16

17 application sonicLiquidFoam;

18

19 startFrom startTime;

20

21 startTime 0;

22

23 stopAt endTime;

24

25 endTime 0.0001;

26

27 deltaT 5e-07;

28

29 writeControl timeStep;

30

31 writeInterval 20;

32

33 purgeWrite 0;

34

35 writeFormat ascii;

36

37 writePrecision 6;

38

39 writeCompression compressed;

40

41 timeFormat general;

42

43 timePrecision 6;

44

45 runTimeModifiable yes;

46

47 // ************************************************************************* //

3.4.4 Выполнение примера

(a) При t = 50 μс (b) При t = 100 μс (c) При t = 150 μс Давление, p(bar)

Рисунок 3.10: Распространение волн давления
Пользователь может выполнить пример и просмотреть результаты в dxFoam. Жидкость вытекает через сопло, вызывая волны, движущиеся вдоль сопла. Как только они достигают входа в резервуар, некоторые из них проходят в резервуар, а другие отражаются. В то время как одни волны отражаются вверх и вниз во входной трубке, волны, проходящие в резервуар, расширяются и распространяются через резервуар. На Рис. 3.10 значения давления показаны в виде контуров так, что фронты волн видны более отчетливо, чем если бы они были изображены в виде обычного графика изолиний.

Если моделирование выполняется достаточно долго и отраженная волна возвращается в трубку, мы видим, что обнаруживается отрицательное абсолютное давление. Моделирование это позволяет, имея некоторые физические предпосылки, т.к. жидкости могут поддерживать напряженные состояния, т.e. могут иметься отрицательныe статические давления.

Однако, в действительности загрязнения или растворенные в жидкости газы могут быть местом образования кавитации или испарения/кипения жидкости, вызываемые низким давлением. Поэтому на практике мы обычно не наблюдаем падение давления ниже давления парообразования в жидкости; по крайней мере, до появления кавитации.

3.4.5 Улучшение решения с усовершенствованием сетки

(a) При t = 50 μс (b) При t = 100 μс (c) При t = 150 μс Давление, p (bar)

Рисунок 3.11: Распространение волн давления с улучшенной сеткой
Посмотрим на изменение во времени поля давления, полученного в результате решения. Отчетливо видно распространение волны давления в резервуаре и многочисленные отражения от внутренних стенок. Также очевидно, что волна давления размывается по ряду ячеек. Сейчас мы можем улучшить сетку и уменьшить временной шаг, чтобы получить более резкое разрешение для фронта. Просто редактируем blockMeshDict и увеличиваем число ячеек на 4 по осям x и y, т.e. блок 0 становится (120 80 1) от (30 20 1) и так далее. Выполняем blockMesh в этом файле. Кроме того, для поддержания значения числа Куранта ниже 1, временной шаг должен быть соответственно уменьшен до с. Повторное моделирование дает значительно лучшее разрешение для волн давления, как показано на Рис. 3.11.