Оглавление 3 Примеры использования вычислительных средств Openfoam 1 1 Обтекание цилиндра 2

• Название: Оглавление 3 Примеры использования вычислительных средств Openfoam 1 1 Обтекание цилиндра 2
• Дата: 02.02.2023
• Размер: 1.64 Mb.
• Имя файла: 1111.doc
• Тип: Глава; #917307
• страница: 5 из 5

3.5 Магнитогидродинамический поток жидкости

В этом примере мы исследуем поток электропроводящей жидкости через магнитное поле. Эта задача принадлежит к области динамики жидкости, известной как магнитогидродинамика (MГД) и применяет mhdFoam.

3.5.1 Постановка задачи

Эта задача известна как задача Хартмана, выбранная для примера т.к. содержит аналитическое решение, с которым можно проверить mhdFoam и определяется следующим образом:
Область решения Область имеет 2 измерения и состоит из потока вдоль двух параллельных пластин, как показано на Рис.3.12.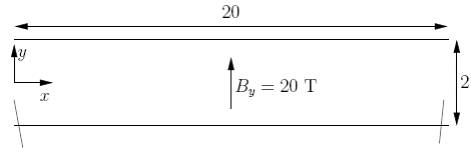



Вход: Ux = 1 м/с Выход: p = 0 bar

Рисунок 3.12: Геометрия задачи Хартмана
Главные уравнения

• Уравнение сохранения массы для несжимаемой жидкости:

(3.20)

•Уравнение количества движения для несжимаемой жидкости6

(3.21)

где B – плотность магнитного потока, .

• Уравнения Максвелла:

(3.22)

где E – напряженность электрического поля.

(3.23)

(3.24)

полагая ∂D/∂t ≪ J. Здесь H – напряженность магнитного поля, J – плотность тока и D – плотность электрического потока.

• Непрерывность заряда:

(3.25)

• Уравнение состояния:

(3.26)

• Закон Ома:

(3.27)

• Комбинируя уравнение 3.22, уравнение 3.24 и уравнение 3.27, и взяв ротор, получим:

(3.28)
Граничныеусловия

• вход обозначает входное условие с фиксированной скоростью U = (1, 0, 0) м/с;

• выход обозначает выходное условие с фиксированным давлением p = 0 Пa;

• upperWall обозначает стенку, где B = (0, 20, 0) T;

• lowerWall обозначает стенку, где B = (0, 20, 0) T;

• передние и задние границы обозначены как «пустые».
Начальные условияU = 0 м/с, p = 100 Пa, B = (0, 20, 0) T.
Свойства переноса

• Кинематическая вязкость ν = 1 Пa с

• Плотность ρ = 1кгм/с

• Электрическая проводимость

• Магнитная проницаемость μ = 1 H/м
Название солвера mhdFoam: код несжимаемой ламинарной магнитогидродинамики.
Название примера задача Хартмана, находится в директории $FOAMTUTORIALS/mhdFoam.

3.5.2 Генерация сетки

Геометрия просто моделируется с числом ячеек 100 по оси x и 40 ячеек по оси y; набор вершин и блоков дан ниже в файле описания сетки:

8 FoamFile

9 {

10 version 2.0;

11 format ascii;

12 class dictionary;

13 object blockMeshDict;

14 }

15 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

16

17 convertToMeters 1;

18

19 vertices

20 (

21 (0 -1 0)

22 (20 -1 0)

23 (20 1 0)

24 (0 1 0)

25 (0 -1 0.1)

26 (20 -1 0.1)

27 (20 1 0.1)

28 (0 1 0.1)

29 );

30

31 blocks

32 (

33 hex (0 1 2 3 4 5 6 7) (100 40 1) simpleGrading (1 1 1)

34 );

35

36 edges

37 (

38 );

39

40 patches

41 (

42 patch inlet

43 (

44 (0 4 7 3)

45 )

46 patch outlet

47 (

48 (2 6 5 1)

49 )

50 patch lowerWall

51 (

52 (1 5 4 0)

53 )

54 patch upperWall

55 (

56 (3 7 6 2)

57 )

58 empty frontAndBack

59 (

60 (0 3 2 1)

61 (4 5 6 7)

62 )

63 );

64

65 mergePatchPairs

66 (

67 );

68

69 // ************************************************************************* //

3.5.3 Выполнение примера

Пользователь может выполнить пример и просмотреть результаты в dxFoam. На этой стадии также полезно с помощью утилиты Ucomponents преобразовать векторное поле U в отдельные скалярные компоненты.

Поток MГД зависит, кроме прочего, от числа Хартмана, которое является мерой соотношения объемной электромагнитной силы и силы вязкости: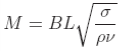

(3.29)

где L – характеристический масштаб длины. В этом случае с By = 20 T, M = 20 и объемные электромагнитные силы доминируют над силами вязкости. Следовательно, с хорошо устойчивым потоком при t = 2 с профиль скорости будет почти плоским, видимым на поперечном сечении в середине домена x = 10 м. Пользователь может построить график Ux в dxFoam. Затем пользователь должен уменьшить плотность магнитного потока B до 1 T и заново выполнить код и Ucomponents. В этом случае M = 1 и объемные электромагнитные силы уже не доминируют. Профиль скорости, следовательно, принимает параболическую форму, характерную для течения Пуазейля как показано на Рис. 3.13. Для проверки этого кода аналитическое решение для профиля скорости Ux сравнивается на Рис. 3.13 с уравнением:

(3.30)

где характеристической длиной L является половина ширины домена, т.e. 1 м.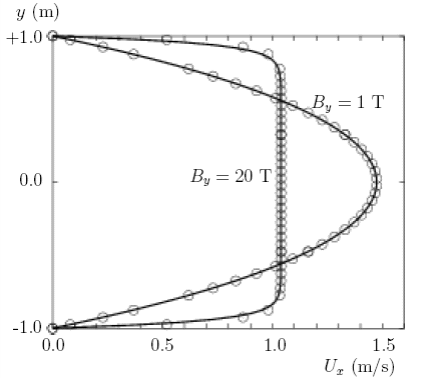



Рисунок 3.13: Профиль скорости в задаче Хартмана при By = 1 T и By = 20 T.