Оглавление 3 Примеры использования вычислительных средств Openfoam 1 1 Обтекание цилиндра 2

• Название: Оглавление 3 Примеры использования вычислительных средств Openfoam 1 1 Обтекание цилиндра 2
• Дата: 02.02.2023
• Размер: 1.64 Mb.
• Имя файла: 1111.doc
• Тип: Глава; #917307
• страница: 1 из 5

Версия OpenFOAM-1.5

Глава 3
Оглавление

3 Примеры использования вычислительных средств OpenFOAM 1

3.1 Обтекание цилиндра 2

3.1.1 Постановка задачи 2

3.1.2 Замечание о солвере potentialFoam 4

3.1.3 Генерация сетки 4

3.1.4 Граничные условия и исходные поля 7

3.1.5 Решение для этого случая 7

3.1.6 Формирование аналитического решения 8

3.1.7 Упражнение 12

3.2 Устойчивый турбулентный поток над ступенькой, обращенной назад по потоку 12

3.2.1 Постановка задачи 12

3.2.2 Генерация сетки 13

3.2.3 Граничные условия и исходные поля 17

3.2.4 Управление решением примера 17

3.3 Сверхзвуковой поток над ступенью, обращенной вперед 19

3.3.1 Постановка задачи 19

3.3.2 Генерация сетки 20

3.3.3 Выполнение примера 22

3.3.4 Упражнение 22

3.4 Декомпрессия резервуара с водой под избыточным внутренним давлением 22

3.4.1 Постановка задачи 23

3.4.2 Генерация сетки 24

3.4.3 Подготовка к выполнению решения 26

3.4.4 Выполнение примера 28

3.4.5 Улучшение решения с усовершенствованием сетки 29

3.5 Магнитогидродинамический поток жидкости 29

3.5.1 Постановка задачи 29

3.5.2 Генерация сетки 31

3.5.3 Выполнение примера 32

3 Примеры использования вычислительных средств OpenFOAM

В этом разделе представлены несколько примеров тестов, поставляемых вместе с описанием OpenFOAM, включая примеры из обучающей программы главы 2 Руководства пользователя, для каждого стандартного солвера (solver – решатель, расчетное математическое обеспечение). Эти примеры приведены для демонстрации некоторых инструментов и свойств OpenFOAM, таких, как численные схемы и алгоритмы в рамках до и после обработки. Также они представляют средства валидации солверов, хотя это и не является их главной функцией.

Каждый пример содержит описание задачи: геометрию, входные и граничные условия, краткое описание решаемых уравнений, использованные модели и требуемые физические свойства. Выбранная область решения может быть частью исходной геометрии, например, если мы вводим симметричные плоскости. Задан метод слияния, обычно blockMesh; конечно же, пользователь может просто просмотреть сетку с каждым примером, расположенным в директории polyMesh, содержащей файлы данных, описывающих эту сетку.

Эти примеры находятся совместно с обучающей программой в поддиректории обучающих средств в инсталляции OpenFOAM. Они объединены солвером в совокупность поддиректорий, например, все случаи icoFoam находятся в поддиректории icoFoam. Прежде чем начать работу с каким-либо частным примером пользователь должен предварительно скопировать его в свой каталог. Мы рекомендуем пользователю сохранять все расчеты в директории, так как обучающие программы копируются в директорию $FOAM RUN. Если структура этой директории еще не создана в каталоге пользователя, ее можно создать с помощью:



Обучающие программы можно затем скопировать в эту директорию с помощью:

3.1 Обтекание цилиндра

В этом примере мы исследуем потенциальный поток вокруг цилиндра, используя potentialFoam.

Этот пример демонстрирует следующие возможности OpenFOAM:

• неортогональные сетки;

• генерация аналитического решения задачи в OpenFOAM.

3.1.1 Постановка задачи

Задача определяется следующим образом:
Областьрешения. Эта область имеет 2 измерения и состоит из квадрата с цилиндром, расположенным в его центре, как это показано на Рис. 3.1.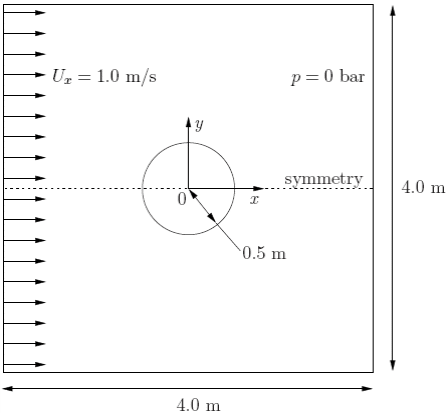



Рисунок 3.1: Геометрия потока вокруг цилиндра
Главные уравнения

• Уравнение неразрывности для несжимаемой жидкости:

(3.1)

• Уравнение давления для несжимаемой, безвихревой жидкости в устойчивом состоянии:

(3.2)
Граничные условия

• Входные (слева) с фиксированной скоростью U = (1, 0, 0) м/с.

• Выходные (справа) с фиксированным давлением p = 0 Пa.

• Несмачиваемая стенка (дно).

• Плоскость симметрии (вершина).
Начальные условияU = 0 м/с, p = 0 Пa — требуемые в OpenFOAM входные файлы, но необязательные для решения задачи в устойчивом состоянии.
Название солвера potentialFoam: код потенциального потока, поток считается несжимаемым, устойчивым, безвихревым, невязким и независящим от гравитации.
Название примера случай цилиндра, расположенного в директории $FOAM TUTORIALS/potentialFoam.

3.1.2 Замечание о солвере potentialFoam

Солвер potentialFoam является полезным для валидации OpenFOAM с допущениями, что для такого потенциального потока существует аналитическое решение в случаях относительно простой геометрии. В примере потока вокруг цилиндра аналитическое решение существует, и мы можем сравнить с ним наше численное решение. Солвер potentialFoam может также работать как утилита для обеспечения стабильного (в разумных пределах) исходного поля U задачи. В некоторых случаях это полезно для исключения нестабильностей, которые могут быть вызваны нестабильным исходным полем.

Коротко говоря, potentialFoam создает стабильное поле из нестабильного исходного поля, заданного пользователем.

3.1.3 Генерация сетки

Генерация сетки с помощью blockMesh описана в обучающих инструкциях в Руководстве пользователя. В этом случае сетка состоит из 10 блоков, как показано на Рис. 3.2. следует помнить, что все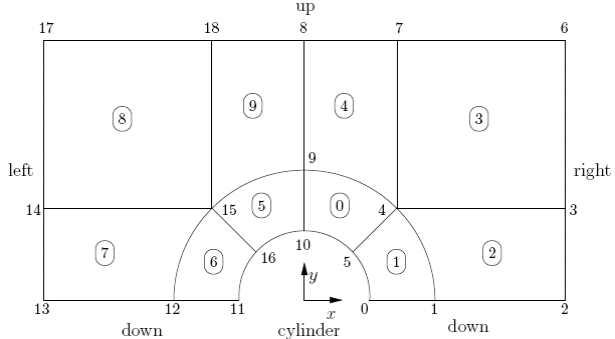



Figure 3.2: Blocks in cylinder geometry

Рис 3.2 Блоки в геометрии цилиндра
сетки в OpenFOAM считаются 3-х мерными. Если мы хотим решать 2-х мерную задачу, мы должны описать 3-х мерную сетку так, что толщина только одной ячейки по третьей оси не учитывается. На Рис. 3.2 показана только задняя плоскость такой геометрии, по оси z = −0.5, а количество вершин пронумерованы 0-18. Остальные 19 вершин на передней плоскости, z = +0.5, пронумерованы так же, как и на задней, что показано ниже в описании сетки:

8 FoamFile

9 {

10 version 2.0;

11 format ascii;

12 class dictionary;

13 object blockMeshDict;

14 }

15 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

16

17 convertToMeters 1;

18

19 vertices

20 (

21 (0.5 0 -0.5)

22 (1 0 -0.5)

23 (2 0 -0.5)

24 (2 0.707107 -0.5)

25 (0.707107 0.707107 -0.5)

26 (0.353553 0.353553 -0.5)

27 (2 2 -0.5)

28 (0.707107 2 -0.5)

29 (0 2 -0.5)

30 (0 1 -0.5)

31 (0 0.5 -0.5)

32 (-0.5 0 -0.5)

33 (-1 0 -0.5)

34 (-2 0 -0.5)

35 (-2 0.707107 -0.5)

36 (-0.707107 0.707107 -0.5)

37 (-0.353553 0.353553 -0.5)

38 (-2 2 -0.5)

39 (-0.707107 2 -0.5)

40 (0.5 0 0.5)

41 (1 0 0.5)

42 (2 0 0.5)

43 (2 0.707107 0.5)

44 (0.707107 0.707107 0.5)

45 (0.353553 0.353553 0.5)

46 (2 2 0.5)

47 (0.707107 2 0.5)

48 (0 2 0.5)

49 (0 1 0.5)

50 (0 0.5 0.5)

51 (-0.5 0 0.5)

52 (-1 0 0.5)

53 (-2 0 0.5)

54 (-2 0.707107 0.5)

55 (-0.707107 0.707107 0.5)

56 (-0.353553 0.353553 0.5)

57 (-2 2 0.5)

58 (-0.707107 2 0.5)

59 );

60

61 blocks

62 (

63 hex (5 4 9 10 24 23 28 29) (10 10 1) simpleGrading (1 1 1)

64 hex (0 1 4 5 19 20 23 24) (10 10 1) simpleGrading (1 1 1)

65 hex (1 2 3 4 20 21 22 23) (20 10 1) simpleGrading (1 1 1)

66 hex (4 3 6 7 23 22 25 26) (20 20 1) simpleGrading (1 1 1)

67 hex (9 4 7 8 28 23 26 27) (10 20 1) simpleGrading (1 1 1)

68 hex (15 16 10 9 34 35 29 28) (10 10 1) simpleGrading (1 1 1)

69 hex (12 11 16 15 31 30 35 34) (10 10 1) simpleGrading (1 1 1)

70 hex (13 12 15 14 32 31 34 33) (20 10 1) simpleGrading (1 1 1)

71 hex (14 15 18 17 33 34 37 36) (20 20 1) simpleGrading (1 1 1)

72 hex (15 9 8 18 34 28 27 37) (10 20 1) simpleGrading (1 1 1)

73 );

74

75 edges

76 (

77 arc 0 5 (0.469846 0.17101 -0.5)

78 arc 5 10 (0.17101 0.469846 -0.5)

79 arc 1 4 (0.939693 0.34202 -0.5)

80 arc 4 9 (0.34202 0.939693 -0.5)

81 arc 19 24 (0.469846 0.17101 0.5)

82 arc 24 29 (0.17101 0.469846 0.5)

83 arc 20 23 (0.939693 0.34202 0.5)

84 arc 23 28 (0.34202 0.939693 0.5)

85 arc 11 16 (-0.469846 0.17101 -0.5)

86 arc 16 10 (-0.17101 0.469846 -0.5)

87 arc 12 15 (-0.939693 0.34202 -0.5)

88 arc 15 9 (-0.34202 0.939693 -0.5)

89 arc 30 35 (-0.469846 0.17101 0.5)

90 arc 35 29 (-0.17101 0.469846 0.5)

91 arc 31 34 (-0.939693 0.34202 0.5)

92 arc 34 28 (-0.34202 0.939693 0.5)

93 );

94

95 patches

96 (

97 symmetryPlane down

98 (

99 (0 1 20 19)

100 (1 2 21 20)

101 (12 11 30 31)

102 (13 12 31 32)

103 )

104 patch right

105 (

106 (2 3 22 21)

107 (3 6 25 22)

108 )

109 symmetryPlane up

110 (

111 (7 8 27 26)

112 (6 7 26 25)

113 (8 18 37 27)

114 (18 17 36 37)

115 )

116 patch left

117 (

118 (14 13 32 33)

119 (17 14 33 36)

120 )

121 symmetryPlane cylinder

122 (

123 (10 5 24 29)

124 (5 0 19 24)

125 (16 10 29 35)

126 (11 16 35 30)

127 )

128 );

129

130 mergePatchPairs

131 (

132 );

133

134 // ************************************************************************* //

3.1.4 Граничные условия и исходные поля

С помощью FoamX или редактируя файлы вручную, установим граничные условия в соответствии с описанием задачи на Рис. 3.1, т.e. левой границей должен быть Вход, правой границей – Выход, а низ и границы цилиндра должны быть плоскостью симметрии (symmetryPlane). Верхние граничные условия выбираются так, что можно проделать наиболее истинное сравнение с нашим аналитическим решением, которое допускает, что область бесконечна по направлению y. В результате нормальный градиент U вдоль плоскости, совпадающей с нашей границей, будет мал. Таким образом, мы налагаем условие, что нормальная компонента равна нулю, т.e. обозначаем границу как symmetryPlane, убеждаясь, что сравнение с аналитическим решением разумно.

3.1.5 Решение для этого случая

После того, как в этой задаче поток предполагается несжимаемым и невязким, не требуется обозначать никаких свойств жидкости. В поддиректории системы controlDict означает контрольные параметры работы. Отметим, что полагая поток стабильным, мы получаем решение только для 1 временного шага:

8 FoamFile

9 {

10 version 2.0;

11 format ascii;

12 class dictionary;

13 object controlDict;

14 }

15 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

16

17 application potentialFoam;

18

19 startFrom startTime;

20

21 startTime 0;

22

23 stopAt endTime;

24

25 endTime 1;

26

27 deltaT 1;

28

29 writeControl timeStep;

30

31 writeInterval 1;

32

33 purgeWrite 0;

34

35 writeFormat ascii;

36

37 writePrecision 6;

38

39 writeCompression uncompressed;

40

41 timeFormat general;

42

43 timePrecision 6;

44

45 runTimeModifiable yes;

46

47 // ************************************************************************* //

potentialFoam выполняет итерационный цикл для уравнения давления, которое решается так, что явные члены, относящиеся к неортогональной коррекции в члене с лапласианом, могут обновляться в последующих итерациях. Число итераций для уравнения давления контролируется с помощью ключа nNonOrthogonalCorrectors в controlDict. Сначала мы можем установить nNonOrthogonalCorrectors в 0 так, что ни один цикл не выполняется,

т.e. уравнение давления решено один раз и неортогональная коррекция отсутствует. Решение показано на Рис. 3.3(a) (при t = 1, когда моделирование устойчивого состояния завершено). Мы ожидаем, что решение покажет гладкие линии течения, проходящие через данную область, как в аналитическом решении на Рис. 3.3 (c), тем не менее, здесь, очевидно, имеется ошибка на участках, где присутствует значительная неортогональность сетки, например, в месте соединения блоков 0, 1 и 3. в этом случае решение выполняется повторно с некоторой неортогональной коррекцией посредством задания величины nNonOrthogonalCorrectors, равной 3. Решение показывает гладкие линии течения без существенных ошибок, благодаря неортогональной коррекции, как это показано на Рис. 3.3 (b).

3.1.6 Формирование аналитического решения

В директорию $FOAMTUTORIALS/potentialFoam/analyticalCylinder включен исходный код для формирования аналитического решения в случае потенциального потока. Скорость в любой точке на расстоянии d под углом θ от центра цилиндра аналитически описывается как:

(3.3)

где r – радиус цилиндра, U∞ – скорость на входе потока. Здесь θ описывает угол по отношению к оси x.

Рассмотрим подробнее исходный код в директории analyticalCylinder. В createFields.H поле скорости считывается при помощи опции IOobject::NO WRITE для подтверждения того, что данные поля не могут быть изменены во время выполнения analyticalCylinder. Скорость на входе и радиус цилиндра взяты из данных, считываемых с сетки, а поле UA

сохраняет аналитическое решение:

1 Info<< "Reading field U\n" << endl;

2 volVectorField U


(a) Без неортогональной коррекции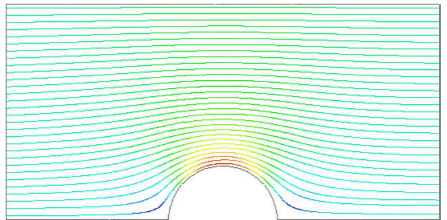



(b) С неортогональной коррекцией


(c) Аналитическое решение

Рисунок 3.3: Линии течения потенциального потока
3 (

4 IOobject

5 (

6 "U",

7 runTime.timeName(),

8 mesh,

9 IOobject::MUST_READ,

10 IOobject::NO_WRITE

11 ),

12 mesh

13 );

14

15 Info<< "Reading inlet velocity uInfX\n" << endl;

16

17 dimensionedScalar uInfX

18 (

19 "uInfx",

20 dimensionSet(0, 1, -1, 0, 0),

21 U.boundaryField()[3][0].x()

22 );

23 Info << "U at inlet = " << uInfX.value() << " m/s" << endl;

24

25 dimensionedScalar radius

26 (

27 "radius",

28 dimensionSet(0, 1, 0, 0, 0),

29 mag(U.mesh().boundary()[4].Cf()[0])

30 );

31

32 Info << "Cylinder radius = " << radius.value() << " m" << endl;

33

34 volVectorField UA

35 (

36 IOobject

37 (

38 "UA",

39 runTime.timeName(),

40 mesh,

41 IOobject::NO_READ,

42 IOobject::AUTO_WRITE

43 ),

44 U

45 );
Главный код analyticalCylinder.C выполняет следующие задачи:

• расширяет временной шаг с помощью runTime++;

• формирует аналитическое решение для поля UA с помощью тензорной математики;

• записывает решение в файл с помощью runTime.writeObjects().



8 License

9 This file is part of OpenFOAM.

10

11 OpenFOAM is free software; you can redistribute it and/or modify it

12 under the terms of the GNU General Public License as published by the

13 Free Software Foundation; either version 2 of the License, or (at your

14 option) any later version.

15

16 OpenFOAM is distributed in the hope that it will be useful, but WITHOUT

17 ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or

18 FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License

19 for more details.

20

21 You should have received a copy of the GNU General Public License

22 along with OpenFOAM; if not, write to the Free Software Foundation,

23 Inc., 51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA

24

25 Application

26 analyticalCylinder

27

28 Description

29 Generates an analytical solution for potential flow around a cylinder.

30 Can be compared with the solution from the potentialFlow/cylinder example.

31

32 \*---------------------------------------------------------------------------*/

33

34 #include "fvCFD.H"

35

36

37 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

38

39 int main(int argc, char *argv[])

40 {

41

42 # include "setRootCase.H"

43

44 # include "createTime.H"

45 # include "createMesh.H"

46 # include "createFields.H"

47

48 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * //

49

50 Info << "\nEvaluating analytical solution" << endl;

51

52 volVectorField centres = UA.mesh().C();

53 volScalarField magCentres = mag(centres);

54 volScalarField theta = acos((centres & vector(1,0,0))/magCentres);

55

56 volVectorField cs2theta =

57 cos(2*theta)*vector(1,0,0)

58 + sin(2*theta)*vector(0,1,0);

59

60 UA = uInfX*(dimensionedVector(vector(1,0,0))

61 - pow((radius/magCentres),2)*cs2theta);

62

63 runTime.write();

64

65 Info<< "end" << endl;

66

67 return(0);

68 }

69

70 // ************************************************************************* //

Эта утилита должна быть скомпилирована с wmake как обычно. Затем она может быть запущена на выполнение набором:
analyticalCylinder $FOAM RUN/potentialFoam цилиндр.
Аналитическое решение в виде линий течения показано графически на Рис. 3.3(c). Заметим, что различия между аналитическим и численным решениями в верхней части плоскости, вызваны тем, что аналитическое решение предполагает бесконечную границу, а численное решение определяет граничное условие как zeroGradient на границе.

3.1.7 Упражнение

Исследуйте точность численного решения выполнением сравнения с аналитическим в analyticalCylinder.