Оглавление 3 Примеры использования вычислительных средств Openfoam 1 1 Обтекание цилиндра 2
 Скачать 1.64 Mb. Скачать 1.64 Mb.
|
3.2 Устойчивый турбулентный поток над ступенькой, обращенной назад по потокуНа этом примере мы исследуем устойчивый турбулентный поток над ступенькой, обращенной назад по потоку. Описание задачи взято из выполненного Pitz и Daily экспериментального исследования, которое можно сравнить с полученным решением. Этот пример вводит следующие новые свойства OpenFOAM: • формирование сетки при помощи blockMesh, используя возможности полностью неравномерной сетки ; • устойчивый турбулентный поток. 3.2.1 Постановка задачиЗадача определяется следующим образом: Область решения. Область имеет 2 измерения, состоит из короткого входа, обращенной назад по потоку ступени и конусообразного сопла на выходе, как это показано на Рис. 3.4. Вход: Ux = 10.0 м/с Выход: p = 0 Пa  Размеры в мм Рисунок 3.4: Геометрия ступени, обращенной назад по потоку Главные уравнения •Уравнение неразрывности для несжимаемой жидкости ∇•U = 0 (3.4) • Уравнение количества движения для устойчивого потока ∇• (UU) + ∇•R = −∇p (3.5) где p – кинематическое давление и (упрощенно) R = νeff∇U – компонента вязкого напряжения с эффективной кинематической вязкостью νeff , вычисленная из выбранных моделей переноса и турбулентности. Начальные условия U = 0 м/с, p = 0 Пa — требуемые в OpenFOAM входные файлы, но необязательные для решения задачи в стационарном состоянии. Граничныеусловия • Вход (слева) с фиксированной скоростью U = (10, 0, 0) м/s; • Выход (справа) с фиксированным давлением p = 0 Пa; • Условия прилипания к стенке на остальных границах. Свойства переноса • Кинематическая вязкость воздуха ν = μ/ρ = 18.1 × 10−6/1.293 = 14.0 μм2/с Модель турбулентности • стандарт • Coefficients: Название солвера simpleFoam: выполнение для устойчивого несжимаемого потока. Название примера pitzDaily, размещенный в директории $FOAMTUTORIALS/simpleFoam. Задача решена с помощью солвера simpleFoam, названного так потому, что выполняется для стационарного течения с помощью Простого алгоритма (SIMPLE algorithm) [**]. Солвер дает полный доступ ко всем моделям турбулентности в библиотеке incompressibleTurbulenceModels и в библиотеке не-Ньютоновских моделей incompressibleTransportModels стандартного издания OpenFOAM. 3.2.2 Генерация сеткиМы ожидаем, что поток в этой задаче имеет разумную сложность и оптимальное решение потребует неравномерной сетки. В общем, области наибольшего сдвига в высокой степени критичны и требуют более тонкой сетки, чем области небольшого сдвига. Мы можем заранее, до расчетов, предусмотреть, где появится большой сдвиг, принимая во внимание каким может быть решение. На входе поток строго однородный по направлению оси x и, так как он проходит над ступенькой, ниже в жидкости образуется сдвиг, формируя вихрь в нижней части области. Таким образом, область большого сдвига будет расположена вблизи центральной линии области и стенок. Область подразделена на 12 блоков, как это показано на Рис. 3.5. Вход Верхняя стенка Выход 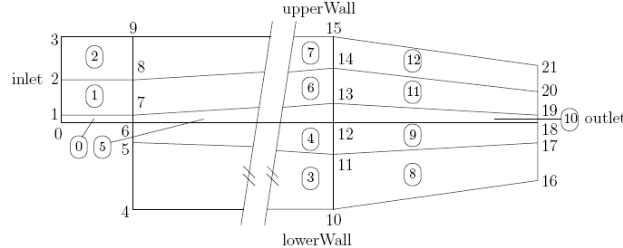 Нижняя стенка Рисунок 3.5: Блоки на ступени, обращенной назад Сетка имеет 3 измерения и, как обычно в OpenFOAM, так и на Рис. 3.5, мы смотрим на заднюю плоскость вдоль оси z = −0.5. Полный набор вершин и блоков дан ниже в файле описания сетки:  8 FoamFile 9 { 10 version 2.0; 11 format ascii; 12 class dictionary; 13 object blockMeshDict; 14 } 15 // * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * // 16 17 convertToMeters 0.001; 18 19 vertices 20 ( 21 (-20.6 0 -0.5) 22 (-20.6 3 -0.5) 23 (-20.6 12.7 -0.5) 24 (-20.6 25.4 -0.5) 25 (0 -25.4 -0.5) 26 (0 -5 -0.5) 27 (0 0 -0.5) 28 (0 3 -0.5) 29 (0 12.7 -0.5) 30 (0 25.4 -0.5) 31 (206 -25.4 -0.5) 32 (206 -8.5 -0.5) 33 (206 0 -0.5) 34 (206 6.5 -0.5) 35 (206 17 -0.5) 36 (206 25.4 -0.5) 37 (290 -16.6 -0.5) 38 (290 -6.3 -0.5) 39 (290 0 -0.5) 40 (290 4.5 -0.5) 41 (290 11 -0.5) 42 (290 16.6 -0.5) 43 (-20.6 0 0.5) 44 (-20.6 3 0.5) 45 (-20.6 12.7 0.5) 46 (-20.6 25.4 0.5) 47 (0 -25.4 0.5) 48 (0 -5 0.5) 49 (0 0 0.5) 50 (0 3 0.5) 51 (0 12.7 0.5) 52 (0 25.4 0.5) 53 (206 -25.4 0.5) 54 (206 -8.5 0.5) 55 (206 0 0.5) 56 (206 6.5 0.5) 57 (206 17 0.5) 58 (206 25.4 0.5) 59 (290 -16.6 0.5) 60 (290 -6.3 0.5) 61 (290 0 0.5) 62 (290 4.5 0.5) 63 (290 11 0.5) 64 (290 16.6 0.5) 65 ); 66 67 blocks 68 ( 69 hex (0 6 7 1 22 28 29 23) (18 7 1) simpleGrading (0.5 1.8 1) 70 hex (1 7 8 2 23 29 30 24) (18 10 1) simpleGrading (0.5 4 1) 71 hex (2 8 9 3 24 30 31 25) (18 13 1) simpleGrading (0.5 0.25 1) 72 hex (4 10 11 5 26 32 33 27) (180 18 1) simpleGrading (4 1 1) 73 hex (5 11 12 6 27 33 34 28) (180 9 1) edgeGrading (4 4 4 4 0.5 1 1 0.5 1 1 1 1) 74 hex (6 12 13 7 28 34 35 29) (180 7 1) edgeGrading (4 4 4 4 1.8 1 1 1.8 1 1 1 1) 75 hex (7 13 14 8 29 35 36 30) (180 10 1) edgeGrading (4 4 4 4 4 1 1 4 1 1 1 1) 76 hex (8 14 15 9 30 36 37 31) (180 13 1) simpleGrading (4 0.25 1) 77 hex (10 16 17 11 32 38 39 33) (25 18 1) simpleGrading (2.5 1 1) 78 hex (11 17 18 12 33 39 40 34) (25 9 1) simpleGrading (2.5 1 1) 79 hex (12 18 19 13 34 40 41 35) (25 7 1) simpleGrading (2.5 1 1) 80 hex (13 19 20 14 35 41 42 36) (25 10 1) simpleGrading (2.5 1 1) 81 hex (14 20 21 15 36 42 43 37) (25 13 1) simpleGrading (2.5 0.25 1) 82 ); 83 84 edges 85 ( 86 ); 87 88 patches 89 ( 90 patch inlet 91 ( 92 (0 22 23 1) 93 (1 23 24 2) 94 (2 24 25 3) 95 ) 96 patch outlet 97 ( 98 (16 17 39 38) 99 (17 18 40 39) 100 (18 19 41 40) 101 (19 20 42 41) 102 (20 21 43 42) 103 ) 104 wall upperWall 105 ( 106 (3 25 31 9) 107 (9 31 37 15) 108 (15 37 43 21) 109 ) 110 wall lowerWall 111 ( 112 (0 6 28 22) 113 (6 5 27 28) 114 (5 4 26 27) 115 (4 10 32 26) 116 (10 16 38 32) 117 ) 118 empty frontAndBack 119 ( 120 (22 28 29 23) 121 (23 29 30 24) 122 (24 30 31 25) 123 (26 32 33 27) 124 (27 33 34 28) 125 (28 34 35 29) 126 (29 35 36 30) 127 (30 36 37 31) 128 (32 38 39 33) 129 (33 39 40 34) 130 (34 40 41 35) 131 (35 41 42 36) 132 (36 42 43 37) 133 (0 1 7 6) 134 (1 2 8 7) 135 (2 3 9 8) 136 (4 5 11 10) 137 (5 6 12 11) 138 (6 7 13 12) 139 (7 8 14 13) 140 (8 9 15 14) 141 (10 11 17 16) 142 (11 12 18 17) 143 (12 13 19 18) 144 (13 14 20 19) 145 (14 15 21 20) 146 ) 147 ); 148 149 mergePatchPairs 150 ( 151 ); 152 153 // ************************************************************************* // Главной чертой этой задачи является применение полностью градуированной сетки blockMesh, как это описано в разделе 5.3.1 Руководства пользователя. Пользователь видит, что блоки 4, 5 и 6 используют полный список 12 коэффициентов расширения, соответствующие каждой грани блока; первые 4 – граням, протяженным в локальном направлении x1, вторые 4 – граням, протяженным в локальном направлении x2 и последние 4 – граням, протяженным в локальном направлении x3. В блоках 4, 5 и 6 коэффициенты равны для всех граней в локальных направлениях x1 и x3, но не для граней в направлении x2, что соответствует всем блокам в общем направлении y. Если мы рассмотрим коэффициенты, применяемые в разделе 5.3.1 Руководства пользователя для определения блоков, мы видим, что степени неравномерности сетки (gradings), установленные вдоль левой и правой граней блоков 4, 5 и 6 на Рис. 3.5, различны. Это проделано с целью формирования тонкой сетки, хорошо соответствующей наиболее критичной области потока, углу ступени и позволяющей расширять оставшуюся часть области. Сетка может быть сформирована с помощью blockMesh из командной строки или с FoamX и выглядеть, как это описано в предшествующих примерах. 3.2.3 Граничные условия и исходные поляФайлы для примера могут быть представлены или редактируемы из FoamX или вручную. В этом случае нам нужно установить исходные (начальные) и граничные поля для скорости U, давления p, турбулентной кинетической энергии k и коэффициента диссипации ε. Граничные условия можно обозначить в FoamX физически: верхнюю и нижнюю стенки определить как Стенка, левую часть – как Вход и правую часть- как Выход. Эти физические граничные условия потребуют от нас определить fixedValue U,kиεна входе. U задано при постановке задачи, но значения ,kиεдолжны быть выбраны пользователем аналогично тому, как это было описано в разделе 2.1.8.1 Руководства пользователя. Предположим, что турбулентность на входе изотропна, а флуктуации оценим как 5% от U на входе, после чего: и Если мы оцениваем длину области турбулентности в 10% от ширины входа: На выходе нужно только определить давление p = 0 Пa. 3.2.4 Управление решением примераfvSchemes выбраны следующим образом: timeScheme должно быть SteadyState; gradScheme и laplacianScheme по умолчанию должны быть Gauss; и divScheme должны быть UD, чтобы обеспечивать ограниченность. Особое внимание должно быть уделено заданию выбора fvTolerances. Хотя верхний уровень кода simpleFoam содержит только уравнения для p и U, турбулентная модель решает уравнения для k, ε и R и задавать точность требуются для всех 5 уравнений. Солвер 10−5 solverTolerance и 0.1 solverRelativeTolerance приемлемы для всех переменных за исключением рекомендованных p 10−6 и 0.01. Требуется задание коэффициента нижней релаксации решения (Under-relaxation) т.к. задача является условно устойчивой. relaxationFactor, равный 0.7 является приемлемым для U, k, ε и R, но для p требуется 0.3 для исключения численной нестабильности. В завершение в controlDict временной шаг deltaT должен быть равен 1, т.к. в примерах устойчивого состояния, таких, как этот, исползуется счетчик итераций. Мы знаем, что решение, требующее 1000 итераций, достигает разумной сходимости, отсюда endTime задается 1000. Зададим величину writeFrequency достаточно большой, например 50, чтобы не заполнить весь диск данными во время работы. 3.2.5 Выполнение примера и последующая обработка Выполним расчет примера и проведем последующую обработку результатов. После нескольких итераций, например, 50, ниже угла ступени образуется вихрь на высоту ступени, но суживающийся по оси x как показано векторами скорости Рис. 3.6(a). После еще нескольких итераций этот вихрь растягивается по оси x от ступени к выходу до тех пор, пока на 1000 итераций система достигнет устойчивого состояния, в котором вихрь полностью сформируется как показано на Рис. 3.6(b-c).  (a) Векторы скорости после 50 итераций  (b) Векторы скорости при 1000 итераций  (c) Линии потока при 1000 итераций Рисунок 3.6: Развитие вихря на ступени, обращенной назад. |
