курсовая математика. математика. Оглавление Введение 3 1 Методы вычисление фрактальной размерности (временного ряда) 4 Заключение 20 Литература 21 Введение
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
ОглавлениеВведение 3 1 Методы вычисление фрактальной размерности (временного ряда) 4 Заключение 20 Литература 21 ВведениеСуществует множество методов количественной оценки фрактальных характеристик структуры с помощью фрактального измерения. В качестве традиционного примера фрактальное измерение пространственной фрактальной структуры может быть определено количественно с помощью фрактального анализа с подсчетом блоков, который исследует способ, которым структура заполняет пространство. Однако такой пространственный анализ, как правило, плохо подходит для анализа так называемых фракталов «временных рядов», которые могут демонстрировать точную или статистическую самоподобность, но которым по своей сути не хватает четко определенных пространственных характеристик. В этой работе мы представляем и исследуем различные методы фрактального анализа, направленные на изучение структур временных рядов. Мы исследуем точность таких методов, применяя каждый метод к наборам сгенерированных компьютером наборов данных временных рядов с четко определенными фрактальными характеристиками. Кроме того, мы исследуем проблемы, связанные с количественной оценкой фрактальных характеристик (и, действительно, с проверкой наличия таких фрактальных характеристик) в трассировках временных рядов, смоделированных так, чтобы они напоминали физические наборы данных. 1 Методы вычисление фрактальной размерности (временного ряда)Математику Бенуа Б. Мандельброту часто приписывают введение понятия дробного, или фрактального, измерения в его статье 1967 года «Какова длина побережья Британии?». На самом деле, однако, любопытная природа измерений береговой линии обсуждалась Льюисом Фраем Ричардсоном за 6 лет до этого в ежегоднике General Systems. Ричардсон, пацифист и математик, попытался исследовать гипотезу о том, что вероятность возникновения войны между парой соседних стран связана с протяженностью общей границы между странами. Как отмечают Ричардсон и Мандельброт, такую гипотезу трудно оценить, поскольку отдельные записи о длине западного побережья Великобритании варьировались в три раза. Действительно, по мере увеличения точности таких измерений, то есть за счет уменьшения длины «линейки», используемой для отслеживания профиля, общая измеренная длина, по-видимому, также увеличивается. Это качество отражает тот факт, что очертания британской береговой линии являются примером «самоподобной» структуры, то есть структуры, которая демонстрирует одни и те же статистические качества или даже точные детали в широком диапазоне масштабов длины. В свете этой очевидной фундаментальной неопределенности Мандельброт утверждает, что знакомые геометрические показатели, такие как длина, неадекватны для описания сложности, встречающейся в природе. Признавая предыдущие исследования Ричардсона, Мандельброт отмечает, что Ричардсон действительно установил эмпирическое соотношение между измеренной длиной побережья L и наименьшей единицей измерения G: L (G) = MG1−D, где M – положительная константа, а D≥1, но отмечает, что «к сожалению, это не привлекло внимания». Основываясь на наблюдениях Ричардсона, Мандельброт вводит формализм дробного, или фрактального, измерения для количественной оценки природы таких форм. Следуя примеру Мандельброта, чтобы обобщить концепцию геометрического измерения, мы можем начать с изучения поведения масштабирования таких тривиально самоподобных объектов, как линия, квадрат и куб. Например, рассмотрим отрезок линии длиной L, который может быть разделен на N неперекрывающихся подмножеств длиной L/N, каждое из которых идентично всему отрезку, но для коэффициента масштабирования r(N)=1/N. Аналогично, квадрат со стороной длиной L может быть разложен на N2 факсимиле длины стороны L/N, каждое из которых уменьшено по сравнению с оригиналом на коэффициент r (N) = N−1/2, а куб со стороной длиной L может быть разложен на N3 факсимиле длины стороны L/N с соответствующим коэффициентом масштабирования r(N)=N−1/3 ; см. Рис. 1. Чтобы обобщить эту закономерность, мы можем заметить, что коэффициент масштабирования r(N) соответствует соотношению r(N)=N−1/D. В этом соотношении D=−log(N)/log(r(N)) известен как измерение подобия рассматриваемой структуры. 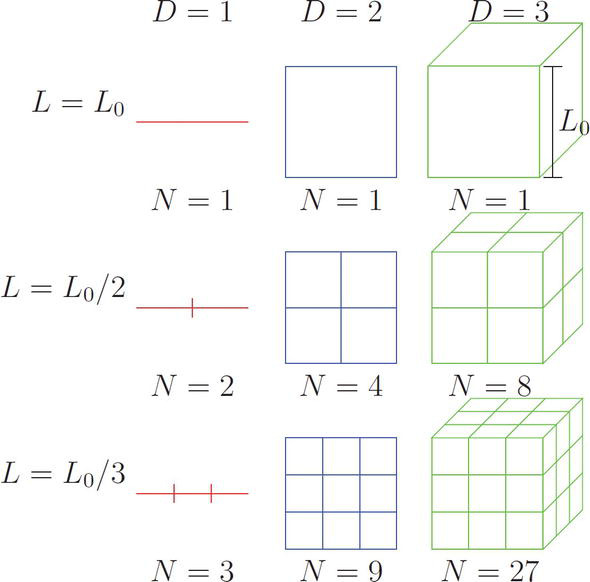 Рисунок 1 Линия, квадрат и куб являются примерами тривиально самоподобных евклидовых фигур. Можно сказать, что евклидова фигура в D измерениях содержит N =(L/L0)−D точных копий самой себя, масштабированных с коэффициентом L/L0. Изображение предоставлено Р.Д. Монтгомери. Применение концепции измерения подобия к менее тривиальным формам является простым в случае точно самоподобных структур, таких как структуры, которые создаются путем итерации генерирующего шаблона. В качестве примера рассмотрим кривую Коха, показанную на рис. 2. Кривая Коха строится следующим образом: начиная с отрезка длины единицы, замените среднюю треть отрезка равносторонним треугольником, основание которого имеет длину 1/3 и перекрывает исходный отрезок линии, затем удалите этот перекрывающийся базовый отрезок. Таким образом, полученная фигура состоит из четырех отрезков, каждый из которых имеет длину 1/3. Повторение этого процесса для каждого нового отрезка линии приводит к последовательности фигур, которые демонстрируют все более тонкую структуру, при этом предельное состояние этого ряда демонстрирует точное самоподобие в том смысле, что нетривиальное подмножество формы в точности идентично целому. Это точное самоподобие показано на рисунке 2, который показывает, что полная кривая Коха может быть описана как сформированная из четырех точных копий самой себя, каждая из которых уменьшена в 1/3 раза. Таким образом, мы можем применить приведенное выше соотношение, чтобы найти, что кривая Коха имеет размерность подобия D =−log(4) /log(1/3)≈1.26. 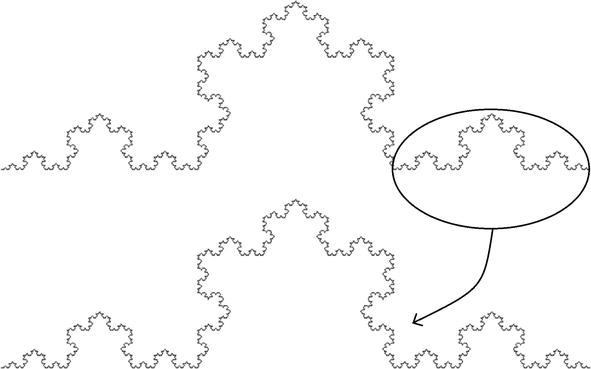 Рисунок 2 Кривая Коха является примером точной самоподобной фигуры с нецелым размером подобия. Измерение подобия, описанное выше, представляет собой лишь один пример множества измерений, которые могут быть определены и вычислены для данной фигуры. Действительно, полезность измерения подобия ограничена тем фактом, что оно применимо только к фигурам, которые демонстрируют точное самоподобие; напротив, сложность, наблюдаемая в природных системах, таких как береговые линии, обычно демонстрирует самоподобие только в статистическом смысле. В качестве примера на рисунке 3 показана структура, которая демонстрирует статистическое самоподобие. В частности, на рисунке 3 показан пример модифицированной кривой Коха, сформированной путем случайного изменения ориентации сегментов линии по мере создания структуры. 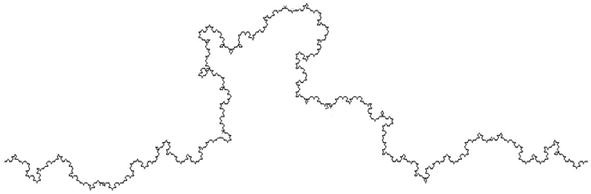 Рисунок 3 Введение случайности в алгоритм генерации кривой Коха приводит к статистически самоподобной фрактальной структуре. В качестве инструмента для количественной оценки природы таких фрактальных структур, которые не демонстрируют точного самоподобия, мы теперь обратимся к (грубо говоря, самоочевидному) «измерению подсчета квадратов», также известному как «покрывающее измерение». Учитывая структуру, которая простирается в двух измерениях2, измерение подсчета ячеек может быть определено следующим образом: сначала наложите квадратную сетку с отдельными ячейками размером ℓ×ℓ на рассматриваемую фигуру и подсчитайте количество ячеек N(ℓ), внутри которых находится некоторая часть рассматриваемой фигуры. присутствует (см. Рис. 4). Затем повторите эту процедуру, изменяя размер блока ℓ, и постройте график log(N(ℓ))vslog(1/ℓ) ; для самоподобной структуры данные должны следовать линейному тренду с градиентом, равным размеру подсчета блоков D. Такой график обычно известный как масштабный график. 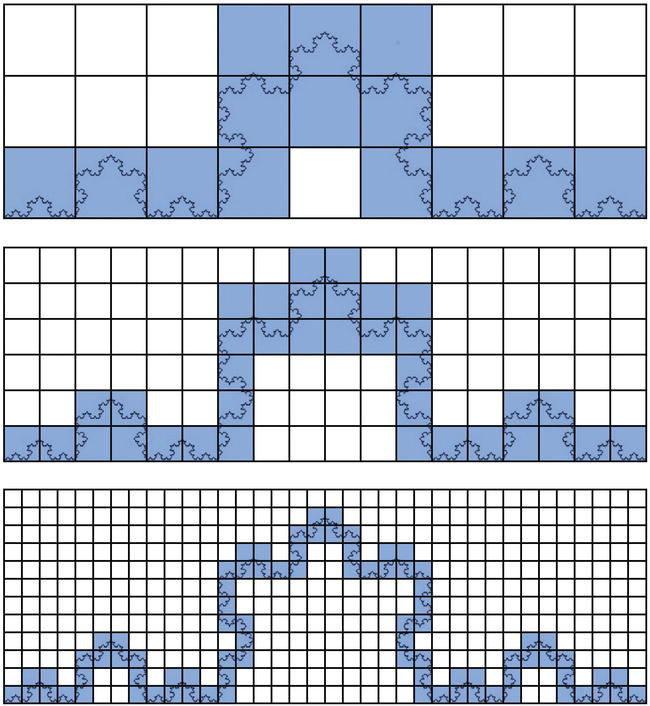 Рисунок 4 Применение метода подсчета ящиков к кривой Коха. Количество ячеек со стороной длиной∝ℓ, занимаемых некоторой частью кривой, следует за N(ℓ)∝ℓ−D, где D – размер кривой, учитывающий количество ячеек. Метод подсчета ящиков также может быть описан в более геометрически понятных терминах. Например, как показано на рис. 4, можно заметить, что набор всех занятых ячеек в заданном масштабе длины ℓ в совокупности служит приближением общей структуры, «наблюдаемой» в масштабе длины ℓ. Иными словами, набор блоков ℓ×ℓ, которые перекрывают некоторую часть базовой структуры, можно рассматривать как представляющий моментальный снимок базовой структуры при просмотре с разрешением, соответствующим длине ℓ. В целом, однако, нельзя ожидать, что набор блоков, покрывающих базовую конструкцию, будет представлять геометрические детали конструкции в любом масштабе длины. Например, как показано на рис. 4, очевидно, что несовместимость прямых краев квадратных прямоугольников и зубчатой границы кривой Коха приводит к заметно грубому представлению структуры во всех масштабах длины, поскольку каждый занятый прямоугольник всегда будет содержать детали, которые не могут быть полностью представлены этим прямоугольником. Хотя метод подсчета квадратов для оценки фрактальной размерности концептуально прост, необходимо соблюдать определенную осторожность, чтобы сохранить полезность метода. Например, необходимо выбрать соответствующий диапазон размеров блока ℓ, в котором можно исследовать тенденцию масштабирования, учитывая, что любая наблюдаемая тенденция фрактального масштабирования не будет сохраняться во всех возможных масштабах длины. То есть для любой конечной структуры можно поместить структуру в рамку размером L×L для соответствующего значения L. В таком случае применение метода подсчета ячеек с ячейками размером ℓ≥L всегда будет возвращать значение N(ℓ)=1 – только одна ячейка может быть заполнена, когда размер ячейки содержит всю структуру, что приводит к кажущейся фрактальной размерности, равной нулю. В качестве другого примера, при рассмотрении диапазона размеров ячеек ℓ≲L почти все такие ячейки будут считаться заполненными, а количество ячеек N(ℓ) будет масштабироваться как квадрат обратного размера ячейки 1/ℓ. В этом случае метод подсчета квадратов вернет кажущуюся фрактальную размерность D= 2, и мы можем сказать, что паттерн «выглядит двумерным» при рассмотрении в этом грубом масштабе. Когда речь идет о закономерностях, встречающихся в природе, также заслуживает рассмотрения противоположная крайность возможных масштабов длины. Для математически сгенерированной фрактальной фигуры, такой как фигура, которая демонстрирует структуру в произвольно малых масштабах длины, метод подсчета ячеек может быть применен с произвольно малыми размерами ячеек ℓ. Однако встречающиеся в природе фрактальные структуры неизменно демонстрируют наименьший масштаб длины, до которого может простираться тенденция к масштабированию. Например, в то время как тенденция масштабирования, безусловно, должна прекратиться в молекулярном и атомном масштабах, такое поведение фрактального масштабирования обычно расходится в масштабах длины, во много раз превышающих это. В таких случаях применение метода подсчета ячеек в масштабах длины ℓ меньших, чем наименьший размер объекта, наблюдаемый в структуре, дает количество заполненных ячеек N (ℓ), которые линейно масштабируются с обратным размером ячейки 1/ℓ; таким образом, фигура «выглядит одномерной» для анализа подсчета ящиков в этих масштабах. Такие условия требуют тщательного определения соответствующего диапазона масштабов длины, в котором можно оценить поведение фрактального масштабирования. Это определение может быть сделано эмпирически, например, путем наблюдения за диапазоном масштабов длины, в котором график масштабирования является достаточно линейным. В качестве альтернативы, это определение может быть принято по соглашению, например, на основе статистических аргументов. На практике, как правило, априори неизвестно, следует ли вообще ожидать, что рассматриваемая структура будет фрактальной, и, следовательно, следует ли ожидать, что она создаст график масштабирования с линейным трендом между отсечениями, определяемыми соответствующими физическими и/или измерительными ограничениями. Соответственно, предпочтительно принимать соглашения с некоторой степенью универсальности, которые не предполагают существования исследуемого поведения фрактального масштабирования. Более конкретно, обычно принимаются следующие соглашения, отмечая, что диапазоны могут быть ограничены физическими и/или измерительными ограничениями. Граница грубомасштабного анализа обычно соответствует пределу диапазона измеряемых масштабов длины, который, в свою очередь, обычно связан с крупномасштабным размером самой структуры. Это ограничение обычно устанавливается на уровне ℓ=L/5, где L – длина стороны наименьшего квадрата, который может ограничивать структуру, что гарантирует, что сетка включает не менее 25 ячеек. Переходя к мелкому масштабу, физический предел определяется наименьшим (нетривиальным) размером объекта, который наблюдается в структуре, в то время как предел измерения в мелком масштабе обычно выбирается для удовлетворения требования, чтобы каждый блок содержал не менее пяти точек данных. На практике выбирается более строгий из этих двух пределов (т.е. больший из физического предела тонкой шкалы и предела измерения тонкой шкалы). В качестве дополнительного соображения при оптимизации производительности метода подсчета ящиков необходимо выбрать положение и ориентацию сетки ящиков относительно рассматриваемой структуры. В той мере, в какой метод подсчета ячеек направлен на исследование присущего структуре качества, наблюдаемая фрактальная размерность не должна зависеть от пространственного перемещения или поворота сетки относительно структуры, поскольку сама структура не имеет предпочтительной ориентации. Однако рассмотрим случай, показанный на рис. 5, в котором метод подсчета квадратов применяется к фрактальному профилю. В схеме подсчета ящиков, рассмотренной выше, все ящики, содержащие любую часть исследуемой структуры, подсчитываются в общую сумму; применяя это к структуре на рисунке 5, мы обнаруживаем, что 35 ящиков заполнены с использованием этого размера коробки ℓ. Предположим, однако, что можно перемещать блоки полунезависимо друг от друга, переводя набор соседних блоков ℓ×ℓ в пределах каждого столбца ширины ℓ. Поступая таким образом, мы обнаруживаем, что тщательное перемещение ячеек внутри этих столбцов приводит к тому, что количество ячеек N(ℓ) уменьшается до 29. Это очевидное несоответствие служит мотивом для уточнения анализа подсчета ящиков, как описано выше. В частности, «метод вариационного подсчета ячеек» включает в себя смещение ячеек в столбцах, как описано выше, чтобы свести к минимуму количество ячеек ℓ×ℓ, необходимых для полного покрытия рассматриваемой цифры. Таким образом, вариационный метод подсчета ящиков служит для устранения некоторой кажущейся двусмысленности традиционного метода подсчета ящиков. Конечно, некоторая двусмысленность все еще остается в этом измененном методе, учитывая, что ориентация вращения колонн относительно исследуемой конструкции остается произвольной. Чтобы устранить эту остаточную двусмысленность, можно повторить описанный выше вариационный метод при различных ориентациях вращения сетки относительно фигуры и выбрать угол, который минимизирует N(ℓ) для каждого значения ℓ. Однако в практических приложениях включение этого дополнительного изменения не оказывает существенного влияния на измеряемые размеры. 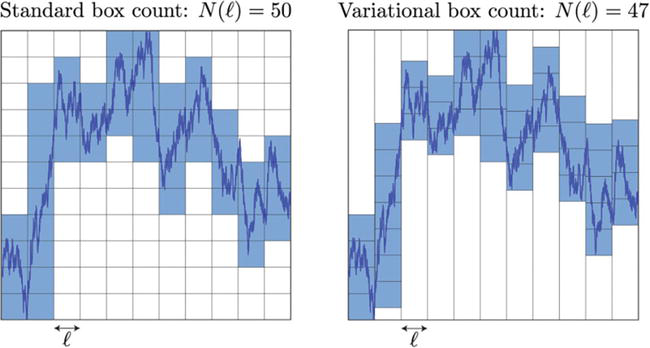 Рисунок 5 Пример применения вариационного метода подсчета ящиков. Когда ячейки ограничены в сетке (слева), мы находим количество ячеек N(ℓ) = 50; однако, когда ячейкам ℓ×ℓ разрешено смещаться по вертикали в пределах столбцов шириной ℓ (справа), измеренное количество ячеек N(ℓ) падает до 47. Фрактальные структуры, рассмотренные выше, в целом представляют собой примеры пространственных фрактальных структур, то есть структур с пространственной протяженностью, фрактальные характеристики которых воплощены в их пространственной форме. Однако многие наблюдаемые структуры и явления демонстрируют фрактальное поведение, не имея при этом пространственной формы. Другим важным классом структур, на которые может быть направлен фрактальный анализ, являются структуры «временных рядов», то есть структуры, которые могут быть представлены как однозначная функция единственной независимой переменной. Как следует из их названия, структура временных рядов может относиться к некоторой переменной величине – скажем, ценам на фондовом рынке или атмосферному давлению, – которая колеблется во времени, но для целей этой работы мы намерены использовать этот термин для обозначения любого набора данных или графика, состоящего из зависимой переменной, которая может быть представлена в виде однозначной функции независимой переменной. Как и в случае с пространственными структурами, рассмотренными выше, структура временных рядов может проявлять свойства фрактального масштабирования либо в статистическом, либо в точном смысле, которые могут быть количественно определены с использованием формализма фрактальных измерений. К сожалению, методы подсчета квадратов, описанные выше для измерения фрактальной размерности, плохо подходят для структур временных рядов. Проще говоря, это ограничение возникает из-за того факта, что методы подсчета квадратов оценивают фрактальную размерность фигур, которые простираются в пространстве, в то время как пространственная «форма» структуры временных рядов по своей сути не определена. То есть, поскольку две оси графика, представляющие набор данных временных рядов, обычно представляют переменные с различными единицами измерения, геометрическое соотношение сторон такого графика принципиально не определено. В качестве примера рассмотрим набор данных, показанный на рисунке 6, который отображает дневную цену закрытия определенной технологической акции за период примерно в 16 лет. В частности, на рис. 6 показаны три представления одного и того же набора данных, причем соответствующая ось y каждой иллюстрации масштабируется на отдельный коэффициент. В качественном плане может возникнуть соблазн сделать вывод, что данные на верхней панели выглядят наиболее линейными, а данные на нижней панели выглядят наиболее заполняющими пространство. Соответственно, учитывая, что метод фрактального анализа с подсчетом ячеек по существу оценивает свойства заполнения пространства структуры, применение анализа с подсчетом ячеек к каждому участку даст отличные результаты для каждого участка. 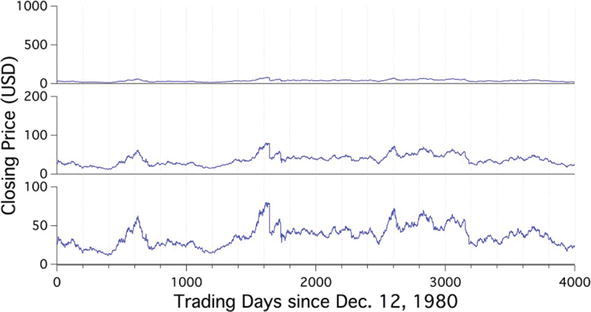 Рисунок 6 Ежедневные цены закрытия одной акции с декабря 1980 по октябрь 1996 года. На каждом из трех графиков отображаются одни и те же данные, но ось y каждого графика масштабируется на отдельный коэффициент. Фрактальный анализ с подсчетом квадратов вернет уникальные результаты для каждого графика несмотря на то, что каждый график представляет один и тот же набор данных. Трудность здесь заключается в том, что фрактальный анализ с подсчетом квадратов обязательно рассматривает фигуру как пространственную сущность, ортогональные размеры которой имеют одинаковые единицы измерения. Напротив, трассировка временных рядов, подобная той, что показана на рис. 6, лишена этого свойства, но все же может демонстрировать фрактальные характеристики в форме либо статистической, либо точной самоподобности. Как обсуждалось выше, точное и статистическое самоподобие описывают структуры, точные детали или статистические свойства которых (соответственно) повторяются при изменении их ортогональных размеров на аналогичный коэффициент. Напротив, точная и статистическая самоподобность относятся к структурам, точные детали или статистические свойства которых (соответственно) повторяются, поскольку их два ортогональных измерения изменяются независимыми величинами. Из-за несоизмеримости ортогональных осей, определяющих трассировку временных рядов, такие структуры не могут проявлять самоподобие, только самоподобие. В качестве примера на рисунке 7 показан набор данных, показанный на рисунке 6, наряду с подмножеством набора данных. Когда это подмножество соответствующим образом масштабируется по каждой из осей x и y, результирующий график разделяет общие статистические свойства исходной трассы и, следовательно, демонстрирует статистическую самоподобность. 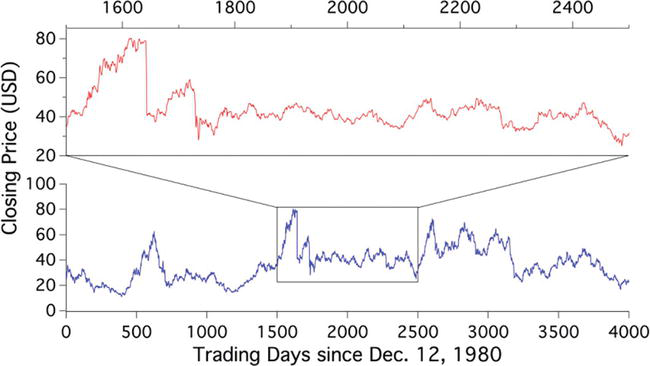 Рисунок 7 Статистическая самоподобность в трассировке фрактальных временных рядов. Выбор подмножества данных о ценах акций, показанных на рис. 6, и масштабирование осей x и y дают трассировку, которая имеет общие статистические свойства с оригиналом. Также возможно, хотя и реже, чтобы трассировка временных рядов демонстрировала точное самоподобие. В качестве примера на рисунке 8 показаны три экспериментально измеренных набора данных, в которых масштабирование осей x и y трасс с помощью тщательно подобранных факторов создает структуры, которые имеют общие характеристики с исходными трасс [5]. 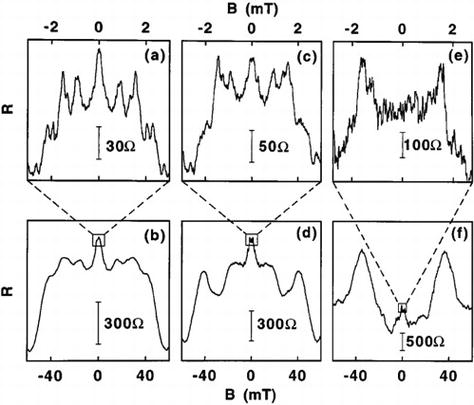 Рисунок 8 Флуктуации магнитосопротивления (MCF), записанные в электронном бильярдном устройстве, могут представлять собой примеры точного сродства к себе в структурах временных рядов. Каждый из трех столбцов на этом рисунке представляет один MCF, наблюдаемый в крупном масштабе (внизу) и мелком масштабе (вверху). Из [5]. Как обсуждалось выше, при применении метода подсчета ячеек к структуре временных рядов измеренные свойства масштабирования структуры будут зависеть от соотношения сторон, с которым представлены данные, что, в свою очередь, является произвольным выбором. Соответственно, применение метода подсчета ячеек к трассировке временных рядов вернет фрактальную размерность, которая по существу является произвольной. Таким образом, необходимо разработать методы фрактального анализа, которые были бы нечувствительны к таким искусственным геометрическим параметрам. Возвращаясь к примеру с рисунком 5 выше, этот рисунок фактически иллюстрирует метод вариационного подсчета боксов применительно к фрактальному профилю в форме фрактала временного ряда. Действительно, фрактальный анализ таких фрактальных структур временных рядов традиционно выполнялся с использованием вариационного метода подсчета ячеек [6,7], который действительно обеспечивает повышение производительности по сравнению с традиционным методом подсчета ячеек с фиксированной сеткой. Тем не менее, вариационный метод подсчета квадратов по-прежнему страдает фатальным недостатком. Чтобы понять, почему это так, рассмотрим графики, показанные на рис. 9. 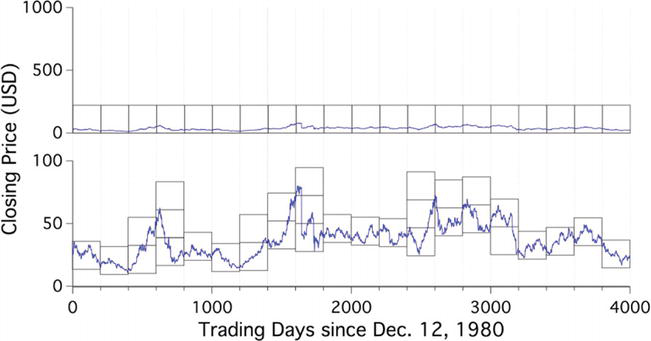 Рисунок 9 Визуализация вариационного метода подсчета квадратов, примененного к данным о ценах акций на рисунках 6 и 7 с «разрешением» ℓ=200 торговых дней. Отображение данных с диапазоном цен от 0 до 100 долларов США дает количество ящиков 37. Отображение данных с диапазоном цен от 0 до 1000 долларов США дает количество коробок, равное 20. Рисунок 9 иллюстрирует данные о ценах акций на рисунках 6 и 7, представленные на двух графиках с осями цен, соответственно масштабированными на два разных фактора, а также визуализацию метода вариационного подсчета, применяемого в масштабе «длины» ℓ=200 торговых дней. Когда показанные цены варьируются от 0 до 100 долларов США (вверху рисунка 9), мы обнаруживаем, что для полного покрытия трассировки требуется минимум 37 коробок. Однако, когда диапазон цен расширяется до 0-1000 долларов США (эффективно увеличивая соотношение сторон данных домен: диапазон; внизу рисунка 9), количество ячеек, необходимых для покрытия трассы, уменьшается до 20. Действительно, количество блоков N(ℓ), необходимых для покрытия «сжатого» графика, будет пропорционально 1 /ℓ для всех значений ℓ, так что блоки «выше», чем диапазон значений, найденных в любом из его столбцов L/ℓ. То есть, пока каждый прямоугольник «выше», чем вертикальный экстент трассировки в каждом столбце, трассировка будет «выглядеть» одномерной. Конечно, фундаментальная проблема заключается в том, что концепция «прямоугольника» ℓ×ℓ на трассировке временных рядов бессмысленна, поскольку вложенная «область» имеет единицы измерения (в данном случае) дней, умноженные на доллары. Хотя в случае анализа пространственного фрактала с подсчетом квадратов вполне разумно наложить пространственную фигуру на прямоугольники четко определенной области, концепция квадрата, нарисованного на графике с несовместимыми и независимо масштабируемыми осями, плохо определена. В некоторых случаях это несоответствие устраняется путем принятия конвенций, устраняющих такую двусмысленность. Например, трассировка временных рядов может быть нормализована по осям x и y таким образом, чтобы область и диапазон графика были от 0 до 1, и структура может быть проанализирована с помощью анализа подсчета квадратов, который использует квадратную сетку, которая просто ограничивает трассировку. Хотя такое соглашение о нормализации может обеспечить согласованный метод исследования относительных свойств масштабирования среди набора связанных трасс временных рядов, абсолютные значения измерений, полученные в результате такого анализа, останутся, по существу, произвольными. ЗаключениеХаотические инварианты, такие как фрактальные измерения, используются для характеристики нелинейных временных рядов. Фрактальная размерность является важной характеристикой систем, поскольку она содержит информацию об их геометрической структуре в нескольких масштабах. Литература1. Высшая математика для экономистов: Учебник / Под ред. Н.Ш. Кремера. – М.: Юнити, 2022. – 479 c. 2. Высшая математика для экономистов. Практикум: Учебное пособие / Под ред. Н.Ш. Кремера. – М.: Юнити, 2020. – 479 c. 3. Высшая математика для экономистов: Учебник / Под ред. Н.Ш. Кремера. – М.: Юнити, 2021. – 479 c. |
