МОТС ЛР1. Ой строки и j

• Название: Ой строки и j
• Дата: 20.10.2022
• Размер: 307.5 Kb.
• Имя файла: МОТС ЛР1.doc
• Тип: Документы; #744448

Цель лабораторной работы  освоить основные понятия теории автоматов и основные методы анализа и синтеза конечных автоматов на абстрактном уровне.

Автоматы в лабораторной работе заданы автоматной таблицей, в которой строки представляют собой состояния, а столбцы – буквы входного алфавита: на пересечении i-ой строки и j-го столбца стоит номер состояния, в которое переходит автомат из i-го состояния по j-ой входной букве, и через запятую – буква выходного алфавита, появляющаяся при этом на выходе автомата (для автоматов Мили). В таком же виде следует представлять и результаты заданий (где это необходимо).
1. Разложить заданный автомат А на автономные:

а) по входным буквам ;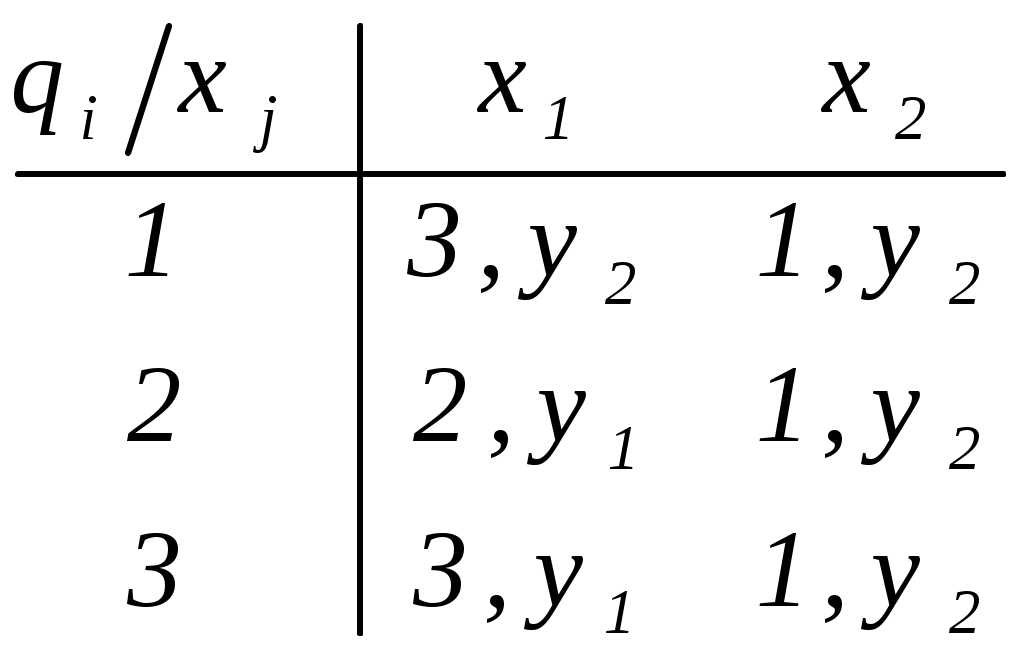



Строим граф: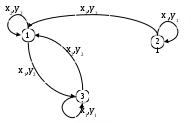


Из автомата с входным алфавитом X =x1, x2 может быть построено 2 различных автономных по входу автоматов исключением из графа переходов автомата всех ребер, кроме ребер с x1 либо x2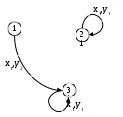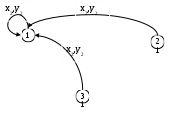

: :

x1 1 3, y2 2 2, y1 3 3, y1

X2 1 1, y2 2 1, y2 3 1, y2

б) 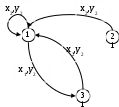Аналогично, автомат называется автономным по выходу, если его выходной алфавит состоит из одной буквы Y = y.

: :

X2 1 1, y2 2 1, y2 3 1, y2

x1 1 2 2, y1 3 3, y1

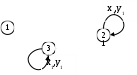
2. По автомату Мили построить эквивалентный ему автомат Мура, используя теорему 4.2.2 [1].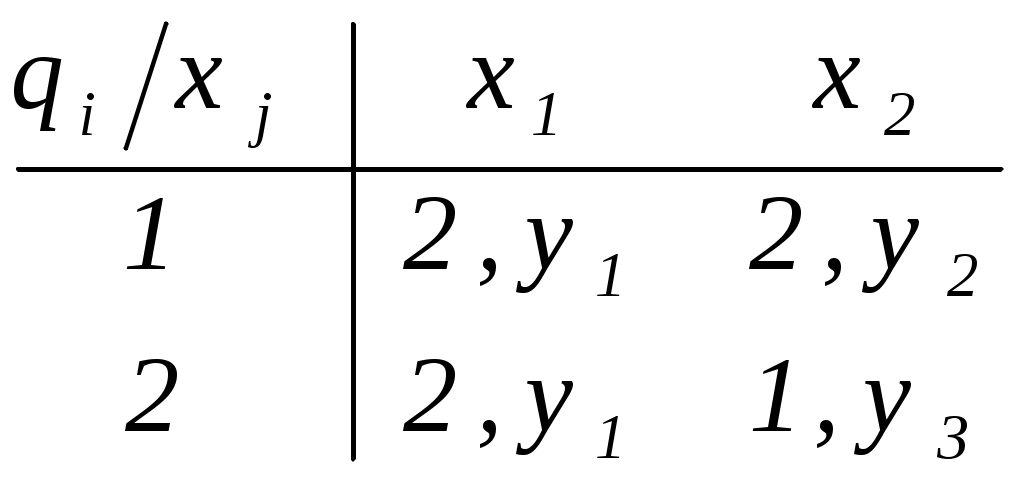


Пусть конечный автомат Мили имеет функцию переходов f_q(q, x) и функцию выходов f_b(q, x). Найдем функцию переходов f_b(b, x) и выходов _b(b) автомата Мура, эквивалентного заданному автомату Мили. Поставим в соответствие каждой паре, включающей состояние q_i и входной сигнал x_j автомата Мили, состояние b_ij автомата Мура. Кроме того, в множестве состояний автомата Мура включим начальное состояние q0 автомата Мили, обозначив его через b0.

Таблица переходов	Таблица выходов
x1 x2 1 2 2 2 2 1	x1 x2 1 y1 y2 2 y1 y3

Такое соответствие представляется в виде таблицы кодирования.

	1 b0	2
x1	2 b01	2 b11
x2	2 b02	1 b12

Таблицу переходов эквивалентного автомата Мура строим в такой последовательности.

1. Выписать из таблицы кодирования состояния автомата Мили и соответствующие каждому состоянию множества состояний автомата Мура:

1 = {b0, b12}

2 = {b01, b02, b11}.

2. Если состояние bij входит в множество, соответствующее состоянию q_р, то в колонку таблицы переходов автомата Мура для состояния bij следует записать состояния, находящиеся в колонке для q_р (таблицы кодирования).

Чтобы отметить выходными сигналами состояния достаточно наложить таблицу выходов автомата Мили на таблицу кодирования состояний автомата Мура и каждое состояние отметить тем выходным сигналом, с которым оно совпадает.

	y1	y1	y1	y2	y3
	b0	b01	b02	b11	b12
x1	2 b01	2 b11	2 b11	2 b11	2 b01
x2	2 b02	1 b12	1 b12	1 b12	2 b02

3. По автомату Мура построить эквивалентный ему автомат Мили.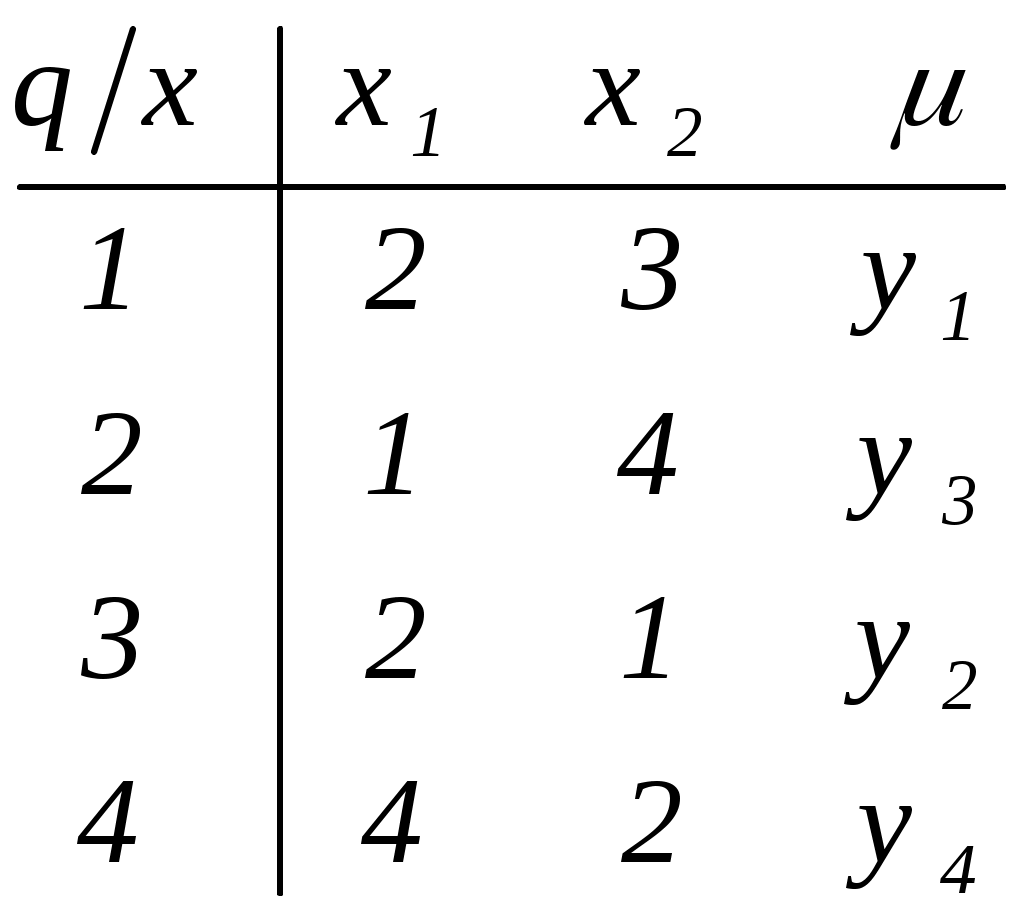


Таблицы переходов автомата Мили и эквивалентного ему автомата Мура совпадают. Таблица выходов автомата Мили составляется так, что в каждую клетку таблицы записывается выходной сигнал, которым отмечено состояние, расположенное в данной клетке.

	x1	x2
1	2, y3	3, y2
2	1, y1	4, y4
3	2, y3	1, y4
4	4, y4	2, y3

4. Найти автоматные отображения слов для заданного автомата, предполагая, что:

а) функция выхода обычная (автомат 1-го рода);

б) функция выхода сдвинутая (автомат 2-го рода).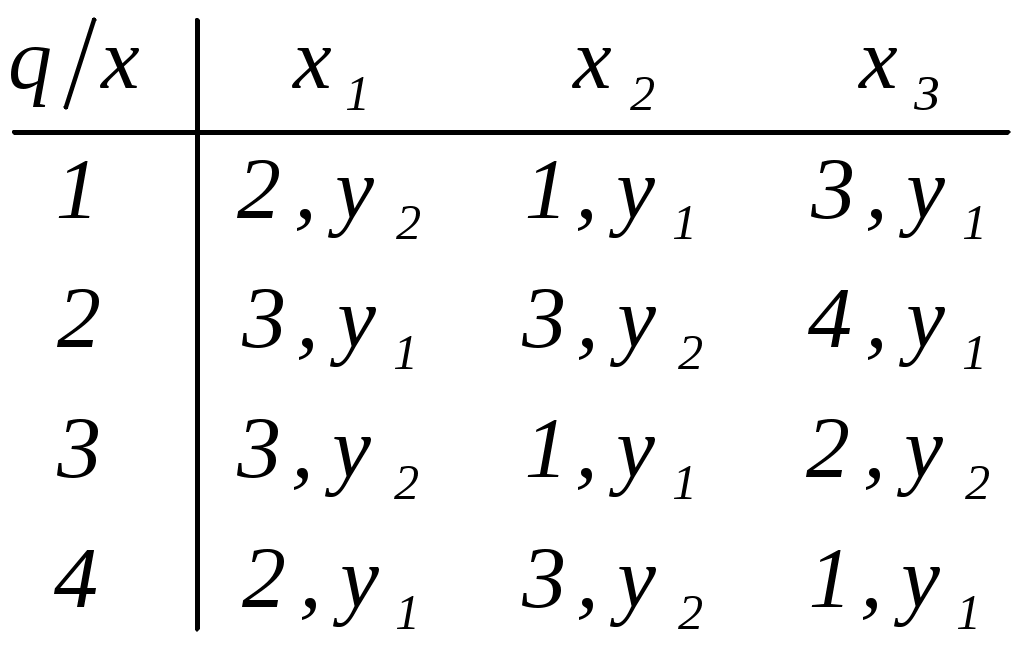

x = x₁x₁x₁x₂x₃x₃x₃

а) q(t) = (q(t-1),x(t)),

y(t) = (q(t-1),x(t)),

S(q_i,x_j) = (q_i,x_j)

S(q_i, xx_j) = S(q_i, x ) (( q_i, x),x_j) –автоматное отбражение.






















































































б) q(t) = (q(t-1),x(t)),

y(t) = (q(t),x(t)),

















5. Минимизировать автомат, используя алгоритм Мили.

Шаг 1. Найдём все классы разбиения, для которых

Разбиение Q = {C_11,C₁₂, C₁₃}, где

C₁₁={1, 9}; C₁₂={2, 5, 6, 7}; C₁₃ = {3, 4, 8},
Состояния 1 и 9 относим к одному классу C_11, т.к.:


Состояния 2, 5, 6 и 7 относим к одному классу C₁₂, т.к.:






Состояния 3, 4 и 8 относим к одному классу C₁₃, т.к.:







Шаг 2. Найдём разбиения среди выделенных классов, для каждого x которых принадлежат одному подклассу C_ij.
Для класса C₁₁, новое разбиение не создаётся, т.к. переходы состояний для каждого x принадлежат одному классу, т.е.:







C₂₁={1, 9};
Аналогично, для класса C₁₂, происходит разбиение на:

C₂₂={2, 6}; C₂₃={5}; C₂₄={7};
Для класса C_13, происходит разбиение на:

C₂₅={3}; C₂₆={4}; C₂₇={8}.
Шаг 3. Найдём разбиения среди выделенных классов
Класс C₂₁ разбивается на:

C₃₁={1}; C₃₂={9};
Класс C₂₂ разбивается на6

C₃₂={2}; C₃₃={6};
Остальные классы не разбиваются.
Шаг 4. Даёт аналогичное разбиение как на предыдущем шаге — алгоритм закончен.
В результате мы получили такое количество классов, как и общее число состояний в исходном автомате. Это означает, что автомат уже минимизирован.
6. Написать формулу в алгебре Клини, задающую событие в алфавите {a, b, c}. Все слова, не начинающиеся на ас или на аb.
– слова не начинающиеся на ac и ab — слова которые начинаются на aa, ba, ca, bb, cb, bc, cc.

И после чего содержат произвольное число символов алфавита:



Либо же слово может состоять из одного символа, следовательно: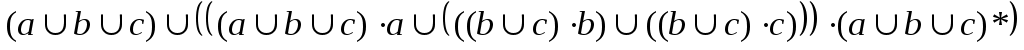



7. Синтезировать автомат (на абстрактном уровне), представляющий регулярное событие.

(bc*)* ba
Строим источники:

Для операции объединения источник будет выглядеть так: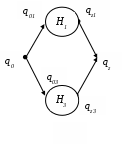



Здесь H₁ = (bc*)*b, а H₃ = a.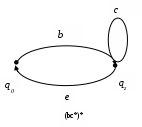


Схематически источник примет такой вид: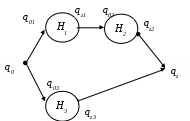






Таким образом, источник для заданного события (bc*)* baимеет вид: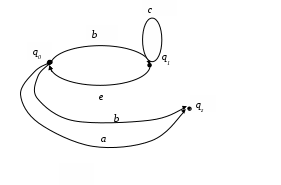


В процессе детерминизации, получаем граф автомата удовлетворяющий исходному событию: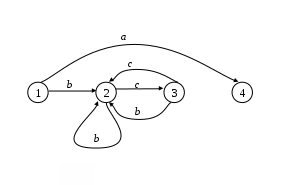



8. Провести анализ автомата (написать выражение регулярного события, представляемого автоматом). Начальное состояние – 1, заключительное – 4.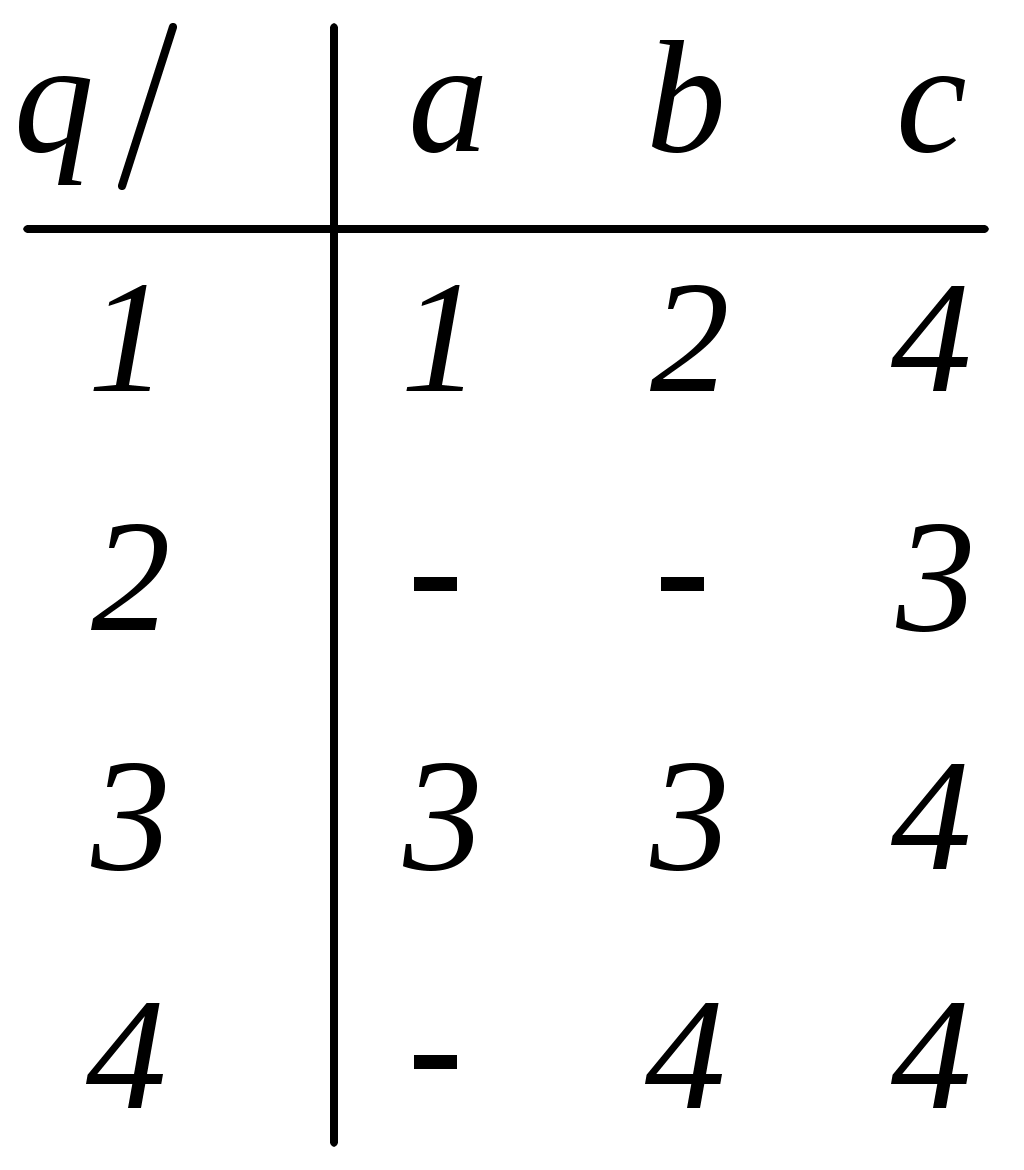


Строим граф: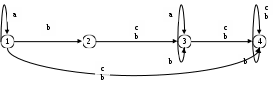



Проведя анализ графа автомата, находим регулярное событие:

a*∙((b∙c∙(ab)*∙c) c)∙(bc)*
Вывод: в ходе выполнения лабораторной работы были освоены основные понятия теории автоматов и основные методы анализа и синтеза конечных автоматов на абстрактном уровне.