Окончание Главы 12-13. Оперативнопроизводственное планирование дискретного производства
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
Задача 13.2Для работ задачи 13.1 было определено время их выполнения. Мы хотели бы определить критический путь и время завершения проекта. Исходные данные приведены в таблице.
Ответ 13.2: Т = 26 дней. Критический путь: 1 – 2 – 3 – 5 – 6 или B – D – E – G. Задача 13.3 Машиностроительная компания специализируется на производстве прополочного оборудования для удаления травы на небольших озерах. Президент компании сознает, что прополка травы машинами значительно лучше, чем использование химикатов для их уничтожения. Химикаты ведут к загрязнению, и трава, кроме того, после употребления химикатов начинает расти быстрее. Поэтому разработчики оборудования обдумывают новую конструкцию машины, которая могла бы вести очистку от травы узких речек и каналов. Работы, необходимые для создания опытного образца, известны. Постройте сеть для этих работ.
Ответ 13.3: смотри рекомендации к решению вручную. Задача 13.4 Для сети предыдущей задачи 13.3 было установлено время выполнения работ. Руководитель проекта хотел бы знать, чему равны ES, EF, LS, LFи резервы для каждой работы, а также критический путь и общее время завершения проектных работ.
Ответ 13.4: Т – 19 дней. Критические пути: A – C – G и B – E – G. Задача 13.5.ПК Компания ведет монтаж электропроводки в жилом доме. Прораб, ведущий работы, весьма обеспокоен сроком выполнения работ: некоторые из его рабочих ненадежны. Список работ и оценки их выполнения – оптимистические, пессимистические и наиболее вероятные приведены в таблице (в днях).
Определите ожидаемое время выполнения и дисперсию времени выполнения каждой работы. Ответ 13.5: смотри рекомендации к решению вручную. Задача 13.6.ПК Продолжим задачу 13.5 и определим также общее время завершения проекта и критический путь выполнения работ по электрификации жилого здания, а также определим ES, EF, LS, LF, Sдля каждой работы. Ответ 13.6: Т = 36.33 недели. Критический путь: С – D – Е – F – Н – К. Задача 13.7 Определите, чему равна вероятность завершения работ в задачах 13.5, 13.6 за сорок дней или менее. Ответ 13.7: .9463. Задача 13.8.ПК Фирма производит по заказам устройства по контролю загрязнения окружающей среды для средних размеров сталелитейных заводов. Самый последний проект, осуществляемый фирмой, состоит из 14 различных работ. Менеджеры хотели бы определить общее время завершения проекта и те работы, которые лежат на критическом пути. Соответствующая информация представлена в таблице.
Ответ 13.8: А – С – Е – Н – I – К – M – N; 50 недель. Задача 13.9.ПК Директор по кадрам разрабатывает программу, которую пользователи могут использовать при поиске работы. Некоторые работы проекта включают подготовку анкетных данных, написание писем, согласование сроков встреч с перспективными работниками, изучение компаний и промышленных предприятий и т. д. Часть необходимой информации представлена в таблице, которая приведена ниже.
а) Постройте сеть этого проекта. б) Определите ожидаемое время и дисперсию каждой работы. в) Определите ES, EF, LS, LF, S для каждой работы. г) Определите критический путь и время завершения проекта. д) Определите вероятность, что проект будет закончен в течение 70 дней. е) Определите вероятность, что проект будет закончен в течение 80 дней. ж) Определите вероятность завершения проекта в течение 90 дней. Ответ 13.9: а), б), в) – см. рекомендации к решению вручную; г) 68.7 дней. Критический путь: A – D – F – H – J – К; д) .644; е) .9993; ж) .9999. Задача 13.10 Используя PERT, яхтсмен получил возможность определить, что ожидаемое время завершения конструирования прогулочной яхты составляет 21 месяц и дисперсия – четыре месяца. а) Какова вероятность завершения проекта через 17 месяцев? б) Какова вероятность завершения проекта через 20 месяцев? в) Какова вероятность завершения проекта через 23 месяца? г) Какова вероятность завершения проекта через 25 месяцев? Ответ 13.10:а) .0228; б) .3085; в) .8413; г) .9772. Задача 13.11.ПК Используя информацию в таблице к задаче 13.9, приведенную выше, определите: а) число недель, которые необходимы для завершения информационной системы; б) работы критического пути; в) резерв каждой работы. Ответ 13.11: а)26 недель; б) A – E – F – I – L – M – N – P; в) см. рекомендации к решению вручную. Задача 13.12 Получение степени в колледже или университете может стать долгой и трудной задачей. Определенные курсы должны быть завершены прежде, чем можно будет приступить к изучению других. Постройте сеть, в которой каждая работа есть определенный учебный курс, который необходимо освоить для получения конкретной степени. Непосредственные предшественники – это курсы, необходимые по условию изучения. Не забудьте рассмотреть все необходимые требования по изучению курсов в университете, на факультете и кафедре. Затем объедините их по семестрам в соответствии с требованиями вашей школы. Сколько времени потребуется для получения степени? Какие курсы, если они не войдут в изучаемую последовательность, смогут повлиять на задержку получения степени? Ответ 13.12: обсудите вопросы на дискуссии в группе. Задача 13.13 Фирма производит металлические хранилища для коммерческого использования. Президент фирмы обдумывает выпуск хранилищ для домашнего использования. Работы, необходимые, чтобы построить экспериментальную модель, и соответствующая информация приведены в таблице.
а) Чему равно время завершения работ? б) Сократите проект до 10 недель, основывая решение на данных о стоимости сокращения времени выполнения работ. Ответ 13.13: а) 14 неделям; б) см. рекомендации к решению вручную. Задача 13.14.ПК «Игл» – новый спроектированный на заказ спортивный автомобиль. Анализ задач создания «Игла» обнаружил следующий перечень соответствующих работ, их непосредственных предшественников, а также время их выполнения.
а) Нарисуйте сеть проекта. б) Отметьте критический путь и определите его протяженность. в) Если «Игл» должен быть завершен на два дня раньше, помогут это осуществить следующие мероприятия: покупка до сборки трансмиссии и рулевого управления; внедрение роботов для ускорения сборки мотора; ускорение доставки спецкомплектующих за три дня. г) Каким образом можно было бы перераспределить ресурсы с других некритических операций, чтобы ускорить работы на критическом пути? Ответ 13.14.ПК: а) см. рекомендации к решению вручную; б) 18 дн.; в) нет, да, нет; г) см. рекомендации к решению вручную. 13.4. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ И РЕШЕНИЯ Задача 13.1.ДОПСледующие представленные здесь работы большого строительного проекта необходимо представить в виде сети, соответствующей выполняемым работам.
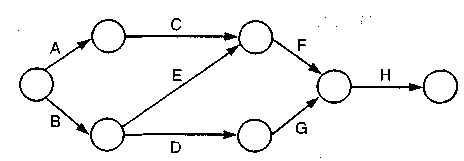 Решение Задача 13.2.ДОП После тщательного анализа каждой работы, которую нам необходимо выполнить, мы получили следующие оценки оптимистического, наиболее вероятного и пессимистического времени и рассчитали ожидаемое время выполнения этих работ и дисперсии (все времена в неделях):
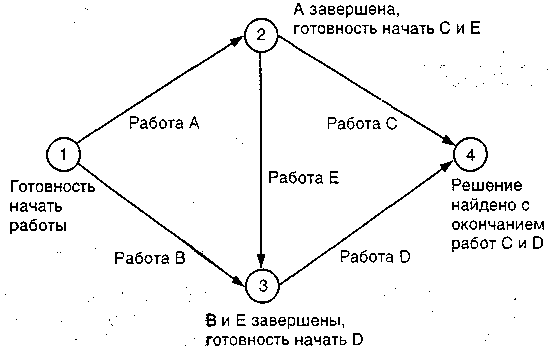 Сетевая модель, представленная на диаграмме внизу, показывает путь решения стоящей перед нами задачи. Задача 13.3.ДОП Реконструируем сеть в 13.2, включив в нее ожидаемое время выполнения работ. 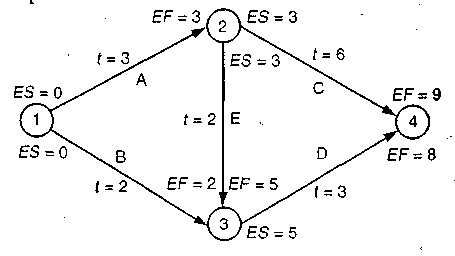 Решение Вначале введем ES (раннее время начала) и EF(раннее время окончания) для всех работ после того, как примем, что проект начинается в момент времени, равный нулю. Обе работы, А и В, могут начаться в момент времени, равный нулю, и закончиться в момент, равный продолжительности их выполнения. ES для работ С и Е равен 3, поскольку обе работы могут начаться только после того, как работа А завершится к моменту времени 3. ES для работ С и Е могут быть найдены добавлением времени их выполнения t к их оценкам ES = 3. Расчет ES работы D дает результат, равный самому большему значению EF работ, входящих в узел 3 и предшествующих началу работы D. Из двух работ В и Е, входящих в узел 3, величина ЕF для работы Е является наибольшей и равной 5. Поэтому ES для работы D равно 5. Действуя подобным образом, получим, что ES для С равно 3. В этом проекте финальное значение EF равно 9 неделям, что соответствует длине критического пути и определяет время завершения проекта вцелом. Задача 13.4.ДОП Следующим шагом будет расчет LS(позднее время начала) и – LF(позднее время окончания) для каждой работы. Вначале LFдля заключительных работ проекта (С и D в этом примере) должны быть равны времени завершения проекта или 9 неделям в этом случае. Для того чтобы завершить работу D к моменту 9, она должна начаться (LS) не позднее момента 6, так как сама работа D длится три недели. Работа С, рассматриваемая аналогичным образом, требует шесть недель для ее выполнения, поэтому ее LS= 9 – 6 = 3. Заметим, что LFдля работы А не может быть рассчитана, пока мы не узнаем LSдля всех следующих за А работ. Поэтому продолжим расчет и прокалькулируем LF для работ В и Е как равные 6 для каждой, поскольку LS для работы D равно 6. Теперь мы можем вычислить LF для этих работ, учитывая, что их продолжительности t = 2 одинаковы. Значит, для обеих работ В и Е позднее время начала LSбудет равно 4. Теперь LF работы А может быть определено как наименьшее работы С или LSработы Е. Оно равно в этом случае 3. LSработы А становится равным LF – tили3 – 3 = 0. Резерв каждой работы теперь может быть рассчитан как LF – ЕFилиLS – ES. Результат сведен в таблицу.
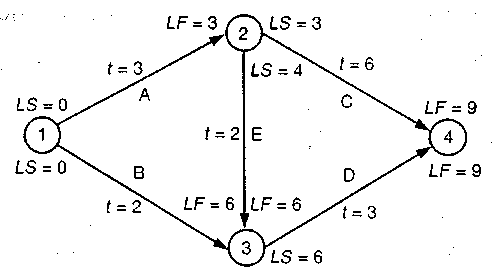 Т Задача 13.5.ДОП Проект имеет ожидаемое время завершения 40 недель и стандартное время отклонения пять недель. Принято, что время завершения проекта распределяется по нормальному закону. а) Какова вероятность того, что проект завершится за 50 недель или менее? б) Какова – вероятность того, что проект завершится за 38 недель или менее? в) Дата завершения проекта должна быть такой, чтобы соответствовать шансу ее выполнения на 90 %. Какова дата завершения проекта? Решение а) Р (X ≤ 50) = Р (Z ≤ 2) = .97725; б) Р (X ≤ 38) = Р (Z ≤ – .4) = .34458; в) величина Z = 1.28. Дата завершения проекта = 40 + 1.28 (5) = 46.4 нед. Задача 13.6.ДОП Развитие новой версии популярного программного обеспечения находится в стадии разработки. Работы, необходимые для завершения проекта, перечислены ниже.
|
