Окончание Главы 12-13. Оперативнопроизводственное планирование дискретного производства
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
УПРАВЛЕНИЕ ПРОЕКТАМИПо тем или иным причинам каждая организация сталкивается с необходимостью выполнять большие и сложные проекты, для управления которыми используются специальные методы. Одним из известных методов, позволяющих достаточно эффективно управлять большими проектами, является временной график Гантта. Однако использование графиков Гантта ограничивается сравнительно несложными проектами. Кроме того, они вызывают сложности с датированием выполняемых работ и, что самое главное, они не отражают адекватно связь между выполняемыми работами и расходуемыми ресурсами. В управлении сложными проектами, состоящими из тысяч работ, эффективнее использовать PERT и СРМ – методы, которые, как правило, компьютеризированы. PERT, который переводится как метод оценки и пересмотра программ, и СРМ – как метод критического пути, оба были разработаны в 50–е годы нашего столетия в США для того, чтобы помочь менеджерам составлять расписания, управлять и оценивать состояние выполнения сложных проектов. В нашей стране методы PERT и СРМ были объединены в метод сетевого планирования и управления. В действительности главным отличием PERT является то, что PERT использует три временных оценки для каждой работы (действия), в результате чего каждая работа оценивается математическим ожиданием времени ее выполнения и дисперсией. СРМ предполагает, что времена всех работ заданы вполне определенно. Но в настоящее время это характеризует лишь гносеологические корни их различия. Практически достоинства обоих методов используются совместно в одном подходе к оценке сложных проектов и в управлении их развитием во времени. Оценка проектов со стороны денежных затрат известна под названием PERT / Cost. Шесть шагов обычны для PERT и СРМ. Процедура следующая: 1. Определить проект и все его основные работы или задачи. 2. Установить все связи между работами. Определить, какие работы должны предшествовать и какие должны следовать за рассматриваемыми работами. 3. Вычертить сеть, содержащую все работы. 4. Определить время и (или) денежные затраты, относящиеся к каждой работе. 5. Рассчитать самый длинный путь на сети от начата исполнения проекта до его окончания (критический путь). 6. Использовать сеть для реализации плана, расписания выполнения работ, управления и контроля за развитием проекта. а) Обозначения: О – событие, определяется временем начала или завершения, имеет смысл точки; → – работа или действие, характеризующееся временем выполнения (стрелка всегда ориентирована в сторону завершения проекта). Для каждой работы в PERT для β – распределения имеем: t = (а + 4т + b) / 6 и где а – оптимистическая оценка продолжительности работы; b – пессимистическая оценка продолжительности работы; т – наиболее вероятное время выполнения работы; t – ожидаемое время выполнения работы;  v – отклонение времени выполнения работы.
b) Целью анализа критического пути является определение следующих характеристик для каждой работы: ES – раннее время начала работы. Все предшествующие работы должны быть завершены до начала данной работы. Время их полного завершения и есть раннее время начала данной работы. LS – позднее время начала работы. Все следующие (за этой работой) работы должны быть завершены без изменения сроков завершения проекта. Это позднее время начала работы без задержки времени выполнения проекта в целом. EF – раннее время окончания работы. LF – позднее время окончания работы. S – время резерва работы (LS – ES) или (LF – EF). Для любой работы мы можем рассчитать ESи LSи можем найти другие три величины следующим образом: EF = ES + t; LF = LS + t; S = LS – ES = LF – EF.
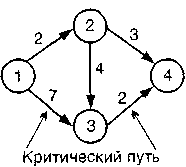 Получив эти оценки для каждой работы, мы можем анализировать весь проект. Типовой анализ проекта включает: 1. Критический путь – группа работ проекта, для которых время резерва Sравно нулю, этот путь критический потому, что задержка в выполнении любой работы на нем ведет к такой же по времени задержке проекта в целом. Это работы 1 – 3 и 3 – 4. 2. Т – общее время выполнения проекта, которое подсчитывается сложением ожидаемых времен t выполнения работ критического пути, оно равно 9 (или 7 + 2). 3. V – отклонение (дисперсия) критического пути, которое подсчитывается сложением отклонений vиндивидуальных работ критического пути, равное 7/6 (или 3/6 + 4/6). c) Ожидаемое время завершения проекта Т равно 20 неделям, и отклонение времени проекта Нравно 100. Какова вероятность того, что проект будет закончен к 25 – й неделе? Т = 20, V= 100. σ = стандартное отклонение = = 10. С – дата желаемого завершения проекта (25 недель). 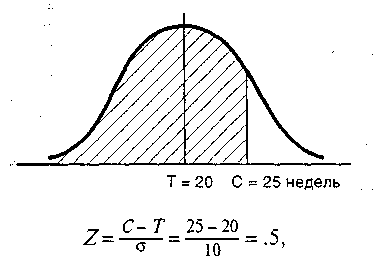 где Z – нормированное отклонение от среднего. Площадь под кривой нормального распределения для Z = .5 есть .6915. Таким образом, вероятность завершения проекта через 25 недель примерно равна .69, или 69%.  d) Дан проект в виде сети работ. 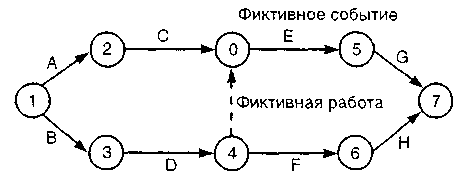 Рассмотрим работу F. Согласно сети, обе работы С и D должны быть завершены прежде, чем начнется F, но в действительности только работа D должна быть завершена. Таким образом, сеть не верна. Добавление фиктивной работы и фиктивного события помогут преодолеть эту проблему, как показано ниже. Теперь в сеть введены все необходимые связи, и она может быть подвергнута анализу, как и прежде. 13.1. ЗАДАЧИ С РЕШЕНИЯМИ Задача 13.1 Постройте сеть, базируясь на следующей информации:
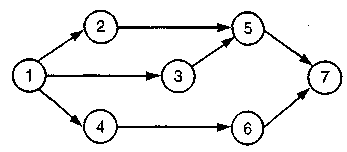 Решение Задача 13.2 Введите фиктивную работу и событие, чтобы откорректировать следующую сеть: 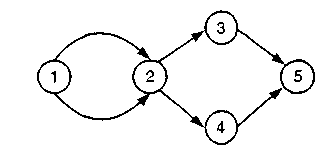 Решение 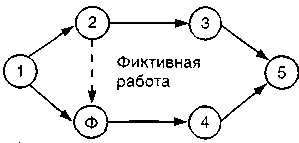 Мы должны добавить фиктивную работу и фиктивное событие, чтобы получить правильную сеть: Задача 13.3 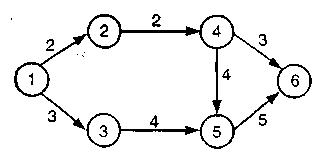 Р
Решение Мы заключили, что критический путь состоит из 1 → 2 → 4 → 5 → 6 работ. Т =2 + 2 + 4 + 5 = 13, V = 2/6 + 4/6 + 2/6 + 1/6 = 9/6 = 1.5/ Задача 13.4 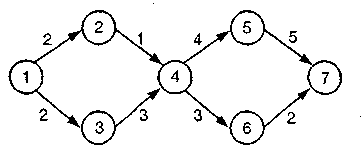 Используя следующую информацию, проделайте анализ критического пути.
Решение Решение начинается с определения ES, EF, LS, LF, S. Мы можем найти эти величины, используя информацию, приведенную в таблице выше, и затем ввести в следующую таблицу:
Затем мы можем найти критический путь, Т и V. Критический путь 1 – 3, 3 – 4, 4 – 5, 5 – 7. T = 2 + 3 + 4 + 5 = 14; V = 1/6 + 2/6 + 4/6 + 1/6 = 9/6. Задача 13.5 Следующая информация была рассчитана по проекту: T = 62нед., V = 81. Какова вероятность того, что проект будет завершен за 18 недель до намеченного срока окончания проекта? Решение Рассматриваемая желаемая дата завершения проекта равна 44 (или 62 – 18)неделям. Кривая нормального распределения будет выглядеть так: 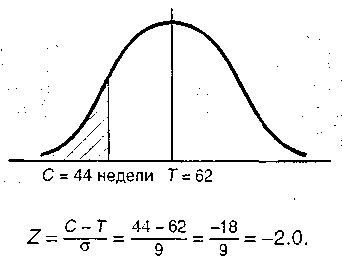 И Задача 13.6 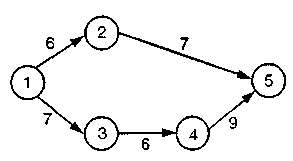 Определите минимум дополнительных затрат, вызываемых уменьшением даты завершения проекта на три месяца.
Мi – максимально возможное уменьшение продолжительности работы i; Сi– дополнительные затраты, вызванные уменьшением времени выполнения работы i; Ki = Сi / Mi– затраты на единицу понижения времени. Решение Первый шаг решения – это определение ES, EF, LS, LF, S для каждой работы.
Критический путь включает следующие работы: 1 – 3, 3 – 4, 4 – 5. Далее определяем К для каждой работы делением С на М.
В заключение выделим ту работу критического пути, которая характеризуется наименьшим значением К. Это работа 4 – 5. В результате мы можем уменьшить время выполнения проекта на один месяц (М = 1 мес.) при дополнительных затратах $200. Мы по – прежнему должны продолжать уменьшение времени выполнения проекта еще на два месяца. Это уменьшение может быть достигнуто согласно листу затрат, соответствующих работам критического пути, путем уменьшения продолжительности выполнения работы 1 – 3 на два месяца с дополнительными затратами в $500. Таким образом, решение выглядит так:
13.2. ВОПРОСЫ ДЛЯ ДИСКУССИИ 1. На какие вопросы могут быть найдены ответы с помощью PERT и СРМ? 2. Что означают понятия «работа», «событие», «непосредственный предшественник»? 3. Опишите, как рассчитываются ожидаемые времена работ и их дисперсии в PERT. 4. Коротко расскажите, что означает анализ критического пути. Какие работы составляют критический путь и почему они важны? 5. Что означают ранние и поздние времена начала работ и как они рассчитываются? 6. Опишите значения резервов и расскажите, как они могут быть определены. 7. Как мы определяем вероятность завершения проекта к определенной дате? Какое допущение делается в этом расчете? 8. Коротко опишите PERT / Cost и как он используется. 9. Чем GERT отличается от PERT? 10. Объясните, почему CPM / MRP является полезным инструментом составления расписаний. ЗАДАЧИ И ОТВЕТЫ Задача 13.1 Директор компании, специализирующейся на консультировании и исследованиях, рассматривает одну из программ обучения менеджеров среднего уровня. Он составил список работ, которые необходимо выполнить до начала выполнения обучающей программы. Работы и их предшествование представлены в таблице.
Постройте сеть для этой задачи. Ответ 13.1: смотри рекомендации к решению вручную. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
