Документ Microsoft Word. Определение уравнения прямой на плоскости
 Скачать 58.18 Kb. Скачать 58.18 Kb.
|
|
Определение уравнения прямой на плоскости Допустим, что есть прямая линия, котору. можно задавать в прямоугольной декартовой системе координат OхуOху. Дадим определение прямой. Определение 1 Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе OxyOxy, будет являться общим уравнением прямой на плоскости. Фактически, уравнением прямой линии на плоскости будем называть уравнение с двумя переменными, которые обозначаются как xx и yy. Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии (линейной точки). Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости (поверхности). Этому будет посвящен весь следующий раздел нашей статьи. Сколько существует вариантов записи? Отметим, что существует несколько вариантов записи уравнения прямой, которые можно сделать. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач. Общее уравнение прямой линии Первым делом познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости (пространстве) в декартовой системе координат Oxy и с ее понятием.Oxy и с ее понятием. Теорема 1 Уравнение вида Ax+By+C=0Ax+By+C=0 , где xx и yy – переменные, а А, ВА, В и CC – это некоторые действительные числа, из которых AA и BB не равны нулю, задает прямую линию в декартовой системе координат OxyOxy. В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида Ax+By+C=0Ax+By+C=0 . Таким образом, общее уравнение прямой на плоскости имеет вид Ax+By+C=0Ax+By+C=0 . Поясним смысл некоторых важных разных аспектов темы. Пример 1 Попробуем это нарисовать. Посмотрите на рисунок. 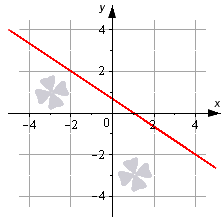 Линию на чертеже стоит определять уравнением вида 2x+3y−2=02x+3y-2=0, так как координаты любой точки, которые будут составлять эту прямую (составляющие), удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2x+3y−2=02x+3y-2=0, дают нам прямую линию, которую мы видим на рисунке. Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А, ВА, В и CC отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида Ax+By=0Ax+By=0 определяет прямую линию, которая проходит через начало координат. Если AA равно нулю, то уравнение Ax+By+C=0Ax+By+C=0 задает прямую, расположенную параллельно оси абсцисс OxOx. Если BB равно нулю, то можно говорить о параллельности линия оси ординат OyOy. Можно вывести: при некотором наборе значений чисел А, ВА, В и CC с помощью общего уравнения прямой можно написать любую прямую линию на плоскости в прямоугольной системе координат OхуOху. Прямая, заданная уравнением вида Ax+By+C=0Ax+By+C=0 , имеет нормальный вектор прямой с координатами (A, B)A, B . Все приведенные уравнения прямых, которые мы по порядку рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой. Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале лекции мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно. Уравнение прямой в отрезках Уравнение прямой в отрезках имеет вид xa+yb=1xa+yb=1 , где aa и bb – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел aa и bb равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат. Благодаря уравнению построение прямой линии на чертеже будет простым делом. Для этого необходимо отметить в прямоугольной системе координат точки (a, 0)a, 0 и (0, b)0, b , а затем начертить прямую линию, которая будет через них проходить. Пример 2 Построим прямую, которая задана формулой x3+y−52=1x3+y-52=1. Отмечаем на графике прямой две точки (3, 0), (0, −52)3, 0, 0, -52, соединяем их между собой. Как это рисовать. 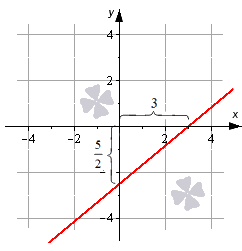 Уравнение прямой с угловым коэффициентом Эти уравнения, имеющие вид y=k⋅x+by=k·x+b должны быть нам хорошо известны из курса алгебры. Здесь xx и yy – это переменные, kk и bb – это некоторые действительные числа, из которых kk представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента xx. Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси OxOx. Определение 2 Для обозначения угла наклона прямой к положительному направлению оси OxOx в декартовой системе координат введем величину угла αα . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол αα считается равным нулю в том случае, если линия параллельна оси OxOx или совпадает с ней. Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывать это будем следующим образом k=tg αk=tg α. Для прямой, которая располагается параллельно оси OyOy или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует). Прямая, которая задана уравнением y=k⋅x+by=k·x+b, проходит через точку (0, b)0, b на оси ординат - это будет означать, что уравнение прямой с угловым коэффициентом y=k⋅x+by=k·x+b задает на плоскости прямую линию, которая проходит через точку (0, b)0, b и образует угол αα с положительным направлением оси OxOx, причем k=tg αk=tg α . Пример 3 Изобразим прямую линию, которая определяется уравнением вида y=√3⋅x−1y=3·x-1. Записываться это будет так. Эта вертикальная линия должна пройти через точку (0, −1)(0, -1) . Угол наклона α=arctg √3=π3α=arctg 3=π3 равен 6060 градусов к положительному направлению оси OxOx. Угловой коэффициент равен √33 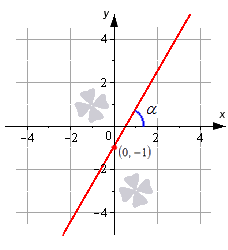 Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции прямой в точке. Каноническое уравнение прямой на плоскости Данный вид уравнения имеет вид x−x1ax=y−y1ayx-x1ax=y-y1ay, где x1, y1, ax, ayx1, y1, ax, ay- это некоторые действительные числа, из которых axax и ayay не равны нулю. Прямая линия, заданная каноническим уравнением прямой, проходит через точку M1(x1, y1)M1(x1, y1) . Числа axax и ayay в знаменателях дробей представляют собой координаты вектора прямой линии, который будет направлять. Это значит, что каноническое уравнение прямой линии x−x1ax=y−y1ayx-x1ax=y-y1ay в декартовой системе координат OxyOxy соответствует линии, проходящей через точку M1(x1, y1)M1(x1, y1) и имеющей направляющий вектор →a=(ax, ay)a→=(ax, ay) . Пример 4 Изобразим в системе координат OxyOxy прямую линию, которая задается уравнением x−2√3=y−31x-23=y-31. Точка M1(2, 3)M1(2, 3) будет иметь принадлежность прямой, вектор →a(√3, 1)a→(3, 1) является направляющим вектором этой прямой линии. 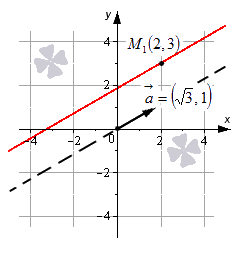 Каноническое уравнение прямой линии вида x−x1ax=y−y1ayx-x1ax=y-y1ay может быть использовано в случаях, когда axax или ayay равно нулю. Наличие ноля в знаменателе делает запись x−x1ax=y−y1ayx-x1ax=y-y1ay условной. Уравнение можно писать следующим образом ay(x−x1)=ax(y−y1)ay(x-x1)=ax(y-y1). В том случае, когда ax=0ax=0 , каноническое уравнение прямой принимает вид x−x10=y−y1ayx-x10=y-y1ay и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью. Каноническое уравнение прямой при условии, что ay=0ay=0, принимает вид x−x1ax=y−y10x-x1ax=y-y10. Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней. Параметрические уравнения прямой на плоскости Данные уравнения имеют вид openx=x1+ax⋅λy=y1+ay⋅λx=x1+ax·λy=y1+ay·λ , где x1, y1, ax, ayx1, y1, ax, ay - это некоторые действительные числа, из которых axax и ayay не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λλ , который может принимать любые действительные значения. Назначение параметрического уравнения в том, чтобы устанавливать неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λλ . Числа (x, y)x, y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λλ . Пример 5 Предположим, что λ=0λ=0 . Тогда openx=x1+ax⋅0y=y1+ay⋅0⇔openx=x1y=y1x=x1+ax·0y=y1+ay·0⇔x=x1y=y1 , т. е. точка с координатами (x1, y1)(x1, y1) принадлежит прямой. Обращаем ваше внимание на то, что коэффициенты axax и ayay при параметре λλ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии. Пример 6 Рассмотрим параметрические уравнения прямой линии вида openx=2+√3⋅λy=3+λx=2+3·λy=3+λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку (x1, y1)(x1, y1) и имеет направляющий вектор →a=(√3, 1)a→=(3, 1) . Нормальное уравнение прямой Нормальное уравнение прямой имеет вид ,Ax+By+C=0Ax+By+C=0, где числа А, ВА, В, и CC таковы, что длина вектора →n=(A, B)n→=(A, B) равна единице, а C≤0C≤0 . Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат OхуOху, является вектор →n=(A,B)n→=(A,B) . Эта прямая проходит на расстоянии openC|C от начала координат в направлении вектора →n=(A, B)n→=(A, B) . Еще одним вариантом записи нормального уравнения прямой линии является cos α⋅x+cos β⋅y−p=0cos α·x+cos β·y-p=0 , где cos αcos α и cos βcos β - это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что →n=(cos α, cos β)n→=(cos α, cos β) , справедливо равенство open→n∣∣=√cos2 α + cos2 β=1n→=cos2 α + cos2 β=1 , величина p≥0p≥0 и равна расстоянию от начала координат до прямой. Пример 7 Рассмотрим общее уравнение прямой −12⋅x+√32⋅y−3=0-12·x+32·y-3=0. Это общее уравнение прямой является нормальным уравнением прямой, так как open→n∣∣=√A2+B2=√(−12)2+(√32)=1n→=A2+B2=-122+32=1 и C=−3≤0C=-3≤0 . Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты (−12, √32)-12, 32 . Линия удалена от начала координат на 33 единицы в направлении нормального вектора →n=(−12, √32)n→=-12, 32 . 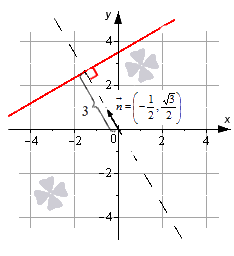 Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости. Если в общем уравнении прямой Ax+By+C=0Ax+By+C=0 числа А, ВА, В и СС таковы, что уравнение Ax+By+C=0Ax+By+C=0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой». |
